文章

首次面试后的算法复盘之链表与二叉树

闲叙一些个人思考，以及记录我在做Hot100中的链表和二叉树部分题目时学习到的一些解法

发表于 更新于
作者 WhythZ
73 分钟阅读
首次面试后的算法复盘之链表与二叉树

反思

第一次失败.png

  • 我从大一开始接触代码（此前的初高中对计算机的理解停留在知道如何给Minecraft装模组光影等上，对工程的理解仅限生电机器哈哈哈），从入学到此次面试前（大二下）并未经历太多的算法题训练（时间都花在写项目了），在上学期学习数据结构时我也仅详细实现了常用的数据结构本身（代码在此仓库）而未专门深入研究算法
  • 面试后我首先尝试从链表和二叉树的题做起，在做完了部分题目后，发现大部分题目十分有趣，解每道题时穷尽一切方法首先以实现为目标，然后再在此基础上自己思考也好参考他人题解也罢对时空复杂度进行优化的过程颇有玩策略游戏的感觉

链表

简单

合并两个有序链表

  • 递归法，空间效率低
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */

ListNode* mergeTwoLists(ListNode* list1, ListNode* list2)
{
    if (list1 == nullptr)
        return list2;
    if (list2 == nullptr)
        return list1;
    
    ListNode* ans;
    if (list1->val < list2->val)
    {
        ans = list1;
        ans->next = mergeTwoLists(list1->next, list2);
    }
    else
    {
        ans = list2;
        ans->next = mergeTwoLists(list1, list2->next);
    }
    return ans;
}
  • 迭代遍历法如下，空间复杂度比递归更好
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

ListNode* mergeTwoLists(ListNode* list1, ListNode* list2)
{
    if (list1 == nullptr)
        return list2;
    if (list2 == nullptr)
        return list1;
    //可以直接开辟在栈区，没必要堆区，销毁挺麻烦
    // ListNode* dummy = new ListNode();
    // ListNode* itr = dummy;
    ListNode dummy;
    ListNode* itr = &dummy;

    while (list1 != nullptr && list2 != nullptr)
    {
        if (list1->val < list2->val)
        {
            itr->next = list1;
            list1 = list1->next;
        }
        else
        {
            itr->next = list2;
            list2 = list2->next;
        }
        itr = itr->next;
    }

    //接上剩余一方的末尾
    itr->next = (list1 == nullptr) ? list2 : list1;
    
    // ListNode* ans = dummy->next;
    // delete dummy;
    // return ans;
    return dummy.next;
}

相交链表

  • 双指针暴力递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

ListNode *getIntersectionNode(ListNode *headA, ListNode *headB)
{
    ListNode* n1 = headA;
    ListNode* n2 = headB;
    
    //n1先动直到末尾，然后n2移动到下一个节点，n1恢复到头部，循环直到n2也到末尾
    while (true)
    {
        //相交的终止条件
        if (n1 == n2)
            return n2;

        //不相交的终止条件
        if (n1->next == NULL && n2->next == NULL)
            return NULL;

        //为进入下一轮循环做准备
        if (n1->next != NULL)
            n1 = n1->next;
        else
        {
            n1 = headA;
            if (n2->next != NULL)
                n2 = n2->next;
        }
    }
}
  • 双指针优化版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

ListNode *getIntersectionNode(ListNode *headA, ListNode *headB)
{
    // if (headA == NULL || headB == NULL)
    //     return NULL;
    
    ListNode* pA = headA;
    ListNode* pB = headB;

    //在同一while循环内同时移动两表头，谁先遍历完自己就顺延到对方头部继续，相当于遍历A+B与B+A
    //若相交，则从交点往后的双方所有节点均一一相等对应，且剩余的节点数一样，必定能被检测出来
    //假设如下两链表aaa和bbbbbb在倒数第二节点（即[1]位置）处相交，必定存在同位相等的情况
    //a[a][a]bbbb[b][b]->a[1][2]bbbb=[1]=[2]
    //bbbb[b][b]a[a][a]->bbbb[1][2]a=[1]=[2]
    while (pA != pB)
    {
        //A+B
        if (pA != NULL)
            pA = pA->next;
        else
            pA = headB;

        //B+A
        if (pB != NULL)
            pB = pB->next;
        else
            pB = headA;
    }
    //跳出循环时，若pA非空则说明相遇，反之则说明二者都遍历到了对方尾部，无相交
    return pA;
}
  • 除了上述巧思解法外，还可引入哈希集合std::unordered_set来避免暴力遍历的时间复杂度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

ListNode *getIntersectionNode(ListNode *headA, ListNode *headB)
{
    ListNode* pA = headA;
    ListNode* pB = headB;

    unordered_set<ListNode*> hset;

    //将第一个链表节点存入哈希集合
    while (pA != NULL)
    {
        hset.insert(pA);
        pA = pA->next;
    }
    //检测第二个链表中是否存在重复
    while (pB != NULL)
    {
        if (hset.count(pB))
            return pB;
        pB = pB->next;
    }
    return NULL;
}

反转链表

  • 递归反接
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

//返回原链表尾指针，即翻转后的链表头指针
ListNode* relink(ListNode* l, ListNode* m, ListNode* r)
{
    m->next = l;
    if (r != nullptr)
        return relink(m, r, r->next);
    return m;
}

ListNode* reverseList(ListNode* head)
{
    if (head == nullptr || head->next == nullptr)
        return head;
    return relink(nullptr, head, head->next);
}
  • 迭代法，省去递归的空间复杂度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

ListNode* reverseList(ListNode* head)
{
    if (head == nullptr || head->next == nullptr)
        return head;

    //保留两级前向节点
    ListNode* left1 = nullptr;
    ListNode* left2 = head;
    while (head != nullptr)
    {
        head = head->next;
        left2->next = left1;
        left1 = left2;
        left2 = head;
    }
    return left1;
}

回文链表

  • 额外数组空间，也可使用栈结构（前半入栈，后半取出对比）来判断，空间复杂度$O(n)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

bool isPalindrome(ListNode* head)
{
    if (head == nullptr || head->next == nullptr)
        return true;

    vector<int> nums;
    while (head != nullptr)
    {
        nums.emplace_back(head->val);
        head = head->next;
    }

    int n = nums.size();
    for (int i = 0; i < n / 2; i++)
    {
        if (nums[i] != nums[n - 1 - i])
            return false;
    }
    return true;
}
  • 将后半链表翻转（此处是递归方法），然后再与前半比较，虽然空间复杂度同样为$O(n)$，但实际比开辟数组更小
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

void relink(ListNode* l, ListNode* m, ListNode* r)
{
    m->next = l;
    if (r != nullptr)
        relink(m, r, r->next);
}

bool isPalindrome(ListNode* head)
{
    if (head == nullptr || head->next == nullptr)
        return true;

    //获取长度与尾指针
    int n = 1;
    ListNode* tail = head;
    while (tail->next != nullptr)
    {
        n++;
        tail = tail->next;
    }

    //翻转后半部分
    int i = 0;
    ListNode* temp = head;
    while (temp != nullptr)
    {
        i++;
        //一旦进入该判断内，在递归完成后temp->next就等于nullptr，循环结束
        if (i > n / 2)
            relink(nullptr, temp, temp->next);
        temp = temp->next;
    }

    //对比两个列表，注意范围是n/2之内（直接忽略奇数总数时的中间节点）
    for (int i = 0; i < n / 2; i++)
    {
        if (head->val != tail->val)
            return false;
        head = head->next;
        tail = tail->next;
    }
    return true;
}
  • 以下是相同思路的另一种写法，更清晰直观
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

ListNode* relink(ListNode* l, ListNode* m, ListNode* r)
{
    m->next = l;
    if (r != nullptr)
        return relink(m, r, r->next);
    return m;
}

bool isPalindrome(ListNode* head)
{
    if (head == nullptr || head->next == nullptr)
        return true;

    //获取长度
    int n = 1;
    ListNode* temp = head;
    while (temp->next != nullptr)
    {
        n++;
        temp = temp->next;
    }

    //翻转后半部分，并获取翻转后的头节点
    temp = head;
    ListNode* newHead;
    for (int i = 1; i <= n / 2; i++)
    {
        //最后一轮时，temp向后移动了(n/2)个节点，n偶则在正中偏右，奇则在正中间
        temp = temp->next;
        if (i == n / 2)
            newHead = relink(nullptr, temp, temp->next);
    }

    //对比两个列表，注意范围是(n/2)之内（直接忽略奇数总数时的中间节点）
    for (int i = 0; i < n / 2; i++)
    {
        if (head->val != newHead->val)
            return false;
        head = head->next;
        newHead = newHead->next;
    }
    return true;
}

环形链表

  • 使用哈希集合存储检测可能重复的节点，时间和空间复杂度均为$O(n)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

bool hasCycle(ListNode* head)
{
    if (head == nullptr || head->next == nullptr)
        return false;
    
    unordered_set<ListNode*> hs;
    while (head != nullptr)
    {
        if (hs.count(head))
            return true;
        hs.insert(head);
        head = head->next;
    }
    return false;
}
  • 假想乌龟和兔子在链表上移动，兔子跑得快，乌龟跑得慢，当乌龟和兔子从链表上的同一个节点开始移动时（龟兔赛跑算法，又称Floyd判圈算法）
    • 若该链表中没有环，那么兔子将一直处于乌龟的前方
    • 若该链表中有环，那么兔子会先于乌龟进入环，并且一直在环内移动，等到乌龟进入环时，由于兔子的速度快，它一定会在某个时刻与乌龟相遇，即套了乌龟若干圈
  • 基于该思想实现的算法空间复杂度优化为$O(1)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

bool hasCycle(ListNode* head)
{
    if (head == nullptr || head->next == nullptr)
        return false;
    
    ListNode* slow = head;
    ListNode* fast = head->next->next;

    while (slow != fast)
    {
        slow = slow->next;
        //快指针速度为慢指针的两倍
        if (fast == nullptr) return false;
        fast = fast->next;
        if (fast == nullptr) return false;
        fast = fast->next;
        if (fast == nullptr) return false;
    }
    return true;
}

//同思路的另一个更好的写法
bool hasCycle(ListNode* head)
{
    if (head == nullptr)
        return false;

    ListNode* slow = head;   
    ListNode* fast = head;

    do
    {
        slow = slow->next;
        if (fast == nullptr) return false;
        fast = fast->next;
        if (fast == nullptr) return false;
        fast = fast->next;
        if (fast == nullptr) return false;
    } while (slow != fast);
    return true;
}

中等

环形链表II

  • 首先使用哈希表能够解决
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

ListNode *detectCycle(ListNode *head)
{
    if (head == nullptr || head->next == nullptr)
        return nullptr;
    
    unordered_set<ListNode*> hs;
    while (head != nullptr)
    {
        if (hs.count(head))
            return head;
        hs.insert(head);
        head = head->next;
    }
    return nullptr;
}
  • 继续考虑使用快慢指针优化
    • 快慢指针相遇后，让慢指针再跑一圈得到圆的长度
    • 然后再在链表头定义两个慢指针，让其中一个先走一圈圆的长度
    • 然后再让两个指针一起走，由于二者速度相同，最终他们必然在圆的起点相遇
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74

ListNode *detectCycle(ListNode *head)
{
    if (head == nullptr || head->next == nullptr)
        return nullptr;
    
    ListNode* slow = head;
    ListNode* fast = head;

    //测试是否成环
    do
    {
        slow = slow->next;
        //快指针速度为慢指针的两倍
        if (fast == nullptr) return nullptr;
        fast = fast->next;
        if (fast == nullptr) return nullptr;
        fast = fast->next;
        if (fast == nullptr) return nullptr;
    } while (slow != fast);
    
    //若执行到此处则说明成环，获取环的周长
    int n = 1;
    ListNode* test = slow->next;
    while (test != slow)
    {
        n++;
        test = test->next;
    }

    //让两个慢指针从头开始向前，复用原来的快慢指针对象
    slow = head;
    fast = head;
    //其中一个先走n步
    for (int i = 0; i < n; i++)
        slow = slow->next;
    //此时二者一起走，则必然在成环处相遇
    while (slow != fast)
    {
        slow = slow->next;
        fast = fast->next;
    }
    return slow;
}

//更优时间复杂度的写法，但更难解释
// ListNode *detectCycle(ListNode *head)
// {
//     if (head == nullptr || head->next == nullptr)
//         return nullptr;
    
//     ListNode* slow = head;
//     ListNode* fast = head;

//     //测试是否成环
//     do
//     {
//         slow = slow->next;
//         //快指针速度为慢指针的两倍
//         if (fast == nullptr) return nullptr;
//         fast = fast->next;
//         if (fast == nullptr) return nullptr;
//         fast = fast->next;
//         if (fast == nullptr) return nullptr;
//     } while (slow != fast);
    
//     //若执行到此处则说明成环，将其一移动到表头重新等速运动，必然在入口相遇
//     fast = head;
//     while (slow != fast)
//     {
//         slow = slow->next;
//         fast = fast->next;
//     }
//     return slow;
// }

两数相加

  • 以下是我第一次想到的方法，逐位进行相加并计算进位
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

ListNode* addTwoNumbers(ListNode* l1, ListNode* l2)
{
    ListNode* backup1 = l1;
    ListNode* backup2 = l2;

    //位和
    int bitsum;
    //是否进位
    bool carry = false;

    //记录谁更长
    bool flag1 = false;
    bool flag2 = false;

    while (l1 != nullptr || l2 != nullptr)
    {
        //使用上一轮进位求和
        bitsum = carry ? 1 : 0;
        if (l1 != nullptr)
            bitsum += l1->val;
        else
            flag1 = true;
        if (l2 != nullptr)
            bitsum += l2->val;
        else
            flag2 = true;

        //检测下一轮是否进位
        carry = false;
        if (bitsum >= 10)
        {
            bitsum -= 10;
            carry = true;
        }

        //应用求取的和，然后向后移动进入下一轮
        if (l1 != nullptr)
        {
            l1->val = bitsum;
            l1 = l1->next;
        }
        if (l2 != nullptr)
        {
            l2->val = bitsum;
            l2 = l2->next;
        }
    }

    //确认答案是谁，并最后进行一次进位
    ListNode* ans;
    if (flag1)
        ans = backup2;
    if (flag2)
        ans = backup1;
    if (carry)
    {
        ListNode* temp = ans;
        while (temp->next != nullptr)
            temp = temp->next;
        temp->next = new ListNode(1);
    }
    return ans;
}

删除链表的倒数第N个结点

  • 最直接的方法就是计算链表长度$L$然后按顺序删除第$(L-N)$个节点，或者使用两次翻转链表，这都是为了解决倒数第$N$，但这样就需要多次扫描，此处就不写代码了
  • 使用队列结构，只需扫描一次，牺牲空间换取时间复杂度最优，注意边界条件
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

ListNode* removeNthFromEnd(ListNode* head, int n)
{
    ListNode* backup = head;

    //扫描一次，用队列存储最新的n+1个节点
    queue<ListNode*> cache;
    while (head != nullptr)
    {
        //新节点入队
        cache.push(head);
        //维持队列长度不超过n+1
        if (cache.size() > n + 1)
            cache.pop();
        //继续扫描
        head = head->next;
    }

    //依据队列长度与n的关系，对边界情况进行判断
    ListNode* l = cache.front();
    int cacheSize = cache.size();
    //此时说明要删除的必然不是头节点
    if (cacheSize == n + 1)
    {
        if (cacheSize >= 3)
        {
            cache.pop();
            cache.pop();
            l->next = cache.front();
        }
        else if (cacheSize == 2)
            l->next = nullptr;
    }
    //此时要删除的必然是头节点
    else if (cacheSize == n)
        return backup->next;
    //最终若执行到此，则正常返回头节点
    return backup;
}
  • 双指针方法，这里的思路和前面”循环链表II”中的快慢指针方法（在最后一步使用两个慢指针，间隔一个圆环周长同速前进，最终会在圆环入口相遇的原理）有异曲同工之妙，使用间隔$(n+1)$距离的两个同速指针，当前方指针到达终点时，后方的指针正好指向目标节点的前一个
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

ListNode* removeNthFromEnd(ListNode* head, int n)
{
    if (head == nullptr)
        return nullptr;

    ListNode* left = head;
    ListNode* right = head;

    //先向前n步
    for (int i = 0; i < n; i++)
        right = right->next;
    //边界条件，此时若right在末尾，则说明链表长度等于n，即要删除的是头节点
    if (right == nullptr)
        return head->next;
    
    //运行到此，right已经领先left了n+1步
    right = right->next;
    //二者一同向前，直到right抵达末尾
    while (right != nullptr)
    {
        left = left->next;
        right = right->next;
    }
    //删除left右侧节点，题目完成
    left->next = left->next->next;
    return head;
}

两两交换链表中的节点

  • 递归，尤其注意helper中的两个备份操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

ListNode* helper(ListNode* front, ListNode* target)
{
    if (target == nullptr)
        return nullptr;
    if (target->next == nullptr)
        return target;
    
    //否则从target开始的链表长度至少为2
    ListNode* backup1 = target->next;
    ListNode* backup2 = target->next->next;
    if (front != nullptr)
        front->next = target->next;
    target->next->next = target;
    //递归调用后再进行链接
    target->next = helper(target, backup2);
    return backup1;
}

ListNode* swapPairs(ListNode* head)
{
    return helper(nullptr, head);
}
  • 另一种更简短的递归写法，但较难读
1
2
3
4
5
6
7
8
9

ListNode* swapPairs(ListNode* head)
{
    if (head == nullptr || head->next == nullptr)
        return head;
    ListNode* newHead = head->next;
    head->next = swapPairs(newHead->next);
    newHead->next = head;
    return newHead;
}
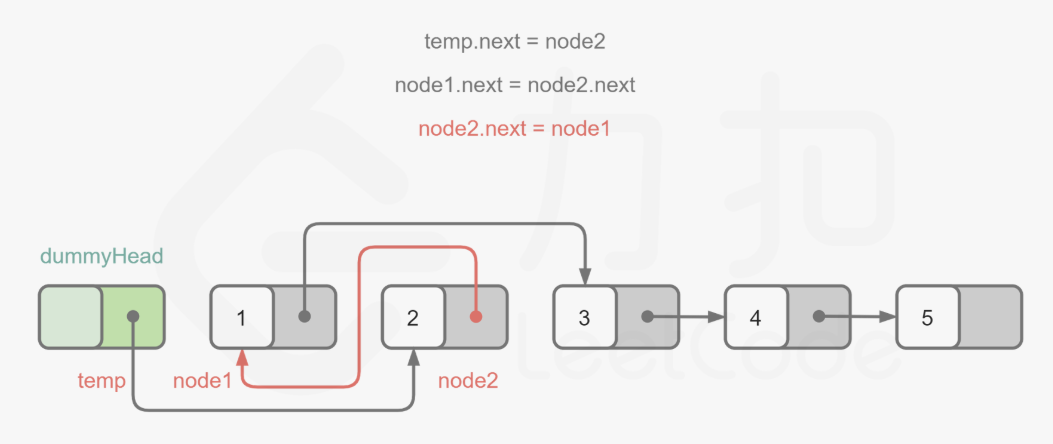
  • 迭代法，省去了递归导致的函数调用堆栈空间复杂度

两两交换链表中的节点迭代法.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

ListNode* swapPairs(ListNode* head)
{
    ListNode* dummyHead = new ListNode(0);
    dummyHead->next = head;

    ListNode* temp = dummyHead;
    while (temp->next != nullptr && temp->next->next != nullptr)
    {
        ListNode* node1 = temp->next;
        ListNode* node2 = temp->next->next;
        temp->next = node2;
        node1->next = node2->next;
        node2->next = node1;
        temp = node1;
    }
    ListNode* ans = dummyHead->next;
    delete dummyHead;
    return ans;
}

随机链表的复制

  • 构建一个以原链表节点为键、新链表节点为值的哈希表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* next;
    Node* random;
    
    Node(int _val) {
        val = _val;
        next = NULL;
        random = NULL;
    }
};
*/

Node* copyRandomList(Node* head)
{
    if (head == NULL)
        return NULL;
    
    //以原链表节点为键、新链表节点为值
    unordered_map<Node*, Node*> hmap;

    //构建新链表节点，并存储键值对
    Node* temp = head;
    while (temp != NULL)
    {
        hmap[temp] = new Node(temp->val);
        temp = temp->next;
    }

    //将离散的新链表节点串联起来，并对random赋值
    temp = head;
    while (temp != NULL)
    {
        hmap[temp]->next = hmap[temp->next];
        hmap[temp]->random = hmap[temp->random];
        temp = temp->next;
    }
    return hmap[head];
}

排序链表

  • 投机取巧方法，直接规定比较规则，然后使用sort，不要在面试时用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

static bool compare(ListNode* l, ListNode* r)
{
    return l->val < r->val;
}

ListNode* sortList(ListNode* head)
{
    if (head == nullptr)
        return nullptr;

    vector<ListNode*> arr;
    while (head != nullptr)
    {
        arr.emplace_back(head);
        head = head->next;
    }

    sort(arr.begin(), arr.end(), compare);
    int n = arr.size();
    for (int i = 1; i < n; i++)
        arr[i - 1]->next = arr[i];
    arr[n - 1]->next = nullptr;

    return arr[0];
}
  • 考虑手撕排序，每次查找第$n$个元素都需从头开始遍历，时间复杂度$O(n)$，除非使用额外空间
    • $O(n^2)$排序：只要涉及跳跃地使用第$n$个元素的排序，均需更大的时间复杂度
    • $O(n\ln n)$排序：堆排序和快速排序需要跳跃地使用第$n$，故只剩下归并排序可以使用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

ListNode* merge(ListNode* list1, ListNode* list2)
{
    if (list1 == nullptr)
        return list2;
    if (list2 == nullptr)
        return list1;
    
    ListNode* ans;
    if (list1->val < list2->val)
    {
        ans = list1;
        list1->next = merge(list1->next, list2);
    }
    else
    {
        ans = list2;
        list2->next = merge(list1, list2->next);
    }
    return ans;
}

ListNode* sortList(ListNode* head)
{
    if (head == nullptr)
        return nullptr;
    if (head->next == nullptr)
        return head;

    //速度差两倍的快慢指针获取中间节点
    ListNode* slow = head;
    ListNode* fast = head;
    while (true)
    {
        fast = fast->next;
        if (fast == nullptr) break;
        fast = fast->next;
        if (fast == nullptr) break;
        slow = slow->next;
    }

    //此时的slow即中间节点，将其与后方链表断链
    ListNode* newHead = slow->next;
    slow->next = nullptr;

    //递归调用排序
    head = sortList(head);
    newHead = sortList(newHead);

    //合并两链表
    return merge(head, newHead);
}

LRU缓存

  • 我首先使用了以下设计，使用数组来维护键的使用更新情况（对于特殊测试用例会超时）
    • 每次添加新键值对直接添加在末尾，时间复杂度为$O(1)$
    • 每次使用或更新特定键的值后，将这个键移动到数组末尾，时间复杂度为$O(n)$
    • 最后使用的键会被维护在数组头部，数组删除头部元素的时间复杂度为$O(n)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

class LRUCache
{
private:
    int capacity;
    unordered_map<int, int> cache;
    vector<int> lru;

    void update(int key)
    {
        //将key对应的元素移到数组末尾
        for (int i = 1; i < lru.size(); i++)
        {
            if (lru[i - 1] == key)
                swap(lru[i - 1], lru[i]);
        }
    }

public:
    LRUCache(int cap): capacity(cap) {}
    
    int get(int key)
    {
        if (cache.count(key))
        {
            //维护使用记录
            update(key);
            return cache[key];
        }
        else
            return -1;
    }
    
    void put(int key, int value)
    {
        if (cache.count(key))
        {
            //维护使用记录
            update(key);
            //修改键对应的值
            cache[key] = value;
        }
        else
        {
            if (cache.size() >= capacity)
            {
                //从两个容器中删除最久未使用的键
                cache.erase(lru[0]);
                lru.erase(lru.begin());
            }

            //初始化使用记录
            lru.emplace_back(key);
            //插入新的键值对
            cache[key] = value;
        }
    }
};

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache* obj = new LRUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */
  • 为了降低时间复杂度，可以想到使用链表来减少因元素和移动删除导致的$O(n)$时间复杂度，以下是最好要使用双向链表的原因
    • 为了时间效率：此题目需对双端均进行访问，一是将最新使用的节点移动到链表某一端（或将新节点直接添加在此端），二是将存放最久未使用的节点移动到另一端（此处需进行删除操作），若用单向链表则会导致其中一端操作的复杂度为$O(n)$
    • 为了前向节点：由于更新键值对使用状况时，需将链表中特定节点移动到链表的一端，这需要将该元素的前后两个节点连接起来，所以为了得到前向节点，必须使用双向链表
  • 在双向链表的实现中，使用伪头部（Dummy Head）和伪尾部（Dummy Tail）标记界限，这样在添加节点和删除节点的时候就不需要检查相邻的节点是否存在，简化代码逻辑
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136

//双向链表节点
struct LinkedNode
{
    int val;
    LinkedNode* prev = nullptr;
    LinkedNode* next = nullptr;

    LinkedNode(int v): val(v) {}
};

//双向链表
struct LinkedList
{
    LinkedNode* dummyHead;
    LinkedNode* dummyTail;

    LinkedList()
    {
        dummyHead = new LinkedNode(-1);
        dummyTail = new LinkedNode(-1);

        dummyHead->next = dummyTail;
        dummyTail->prev = dummyHead;
    }

    ~LinkedList()
    {
        delete dummyHead;
        delete dummyTail;
    }

    //将新节点推送到链表头部
    void add(int v)
    {
        LinkedNode* temp = new LinkedNode(v);
        //使用伪头尾节点的好处，即无需判空相关的复杂逻辑
        temp->prev = dummyHead;
        temp->next = dummyHead->next;
        dummyHead->next->prev = temp;
        dummyHead->next = temp;
    }

    //删除链表末尾节点，即最久未使用的节点，并返回该节点的值，即哈希表所用的键
    int erase()
    {
        //链表中无节点，无法删除
        if (dummyHead->next == dummyTail)
            return -1;
        
        //运行到此处说明至少存在一个节点，获取其值
        int key = dummyTail->prev->val;
        
        //重新链接
        LinkedNode* backup = dummyTail->prev->prev;
        backup->next = dummyTail;
        //释放该节点空间
        delete dummyTail->prev;
        dummyTail->prev = backup;

        //成功删除，返回
        return key;
    }

    //更新使用状态，将最新使用的节点放在最前方
    void update(int key)
    {
        //找到key对应的节点
        LinkedNode* temp = dummyHead;
        while (temp->next != dummyTail)
        {
            temp = temp->next;
            if (temp->val == key)
            {
                //重新桥接前后两节点
                temp->prev->next = temp->next;
                temp->next->prev = temp->prev;

                //将目标元素放到链表头部
                temp->next = dummyHead->next;
                temp->prev = dummyHead;
                dummyHead->next->prev = temp;
                dummyHead->next = temp;

                //结束循环
                break;
            }
        }
    }
};

class LRUCache
{
private:
    int capacity;
    unordered_map<int, int> cache;
    //使用双向链表
    LinkedList lru;

public:
    LRUCache(int cap): capacity(cap) {}
    
    int get(int key)
    {
        if (cache.count(key))
        {
            //更新使用记录
            lru.update(key);
            return cache[key];
        }
        else
            return -1;
    }
    
    void put(int key, int value)
    {
        if (cache.count(key))
        {
            //更新使用记录
            lru.update(key);
            //修改键对应的值
            cache[key] = value;
        }
        else
        {
            if (cache.size() >= capacity)
            {
                //删除最久未使用的节点，并获取其键，将其从哈希表中删除
                cache.erase(lru.erase());
            }
            //初始化使用记录
            lru.add(key);
            //插入新的键值对
            cache[key] = value;
        }
    }
};
  • 上述代码遇到同一个超长测试用例还是超时了，那我们只能再申请一个以LRU缓存中的键为键，以链表节点为值得哈希表，以空间换时间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151

//双向链表节点
struct LinkedNode
{
    int val;
    LinkedNode* prev = nullptr;
    LinkedNode* next = nullptr;

    LinkedNode(int v): val(v) {}
};

//双向链表
struct LinkedList
{
    unordered_map<int, LinkedNode*> hmap;
    LinkedNode* dummyHead;
    LinkedNode* dummyTail;

    LinkedList()
    {
        dummyHead = new LinkedNode(-1);
        dummyTail = new LinkedNode(-1);

        dummyHead->next = dummyTail;
        dummyTail->prev = dummyHead;
    }

    ~LinkedList()
    {
        delete dummyHead;
        delete dummyTail;
    }

    //将新节点推送到链表头部
    void add(int v)
    {
        //创建新节点，并加入到哈希表内
        LinkedNode* temp = new LinkedNode(v);
        hmap[v] = temp;
        //使用伪头尾节点的好处，即无需判空相关的复杂逻辑
        temp->prev = dummyHead;
        temp->next = dummyHead->next;
        dummyHead->next->prev = temp;
        dummyHead->next = temp;
    }

    //删除链表末尾节点，即最久未使用的节点，并返回该节点的值，即哈希表所用的键
    int erase()
    {
        //链表中无节点，无法删除
        if (dummyHead->next == dummyTail)
            return -1;
        
        //运行到此处说明至少存在一个节点，获取其值
        int key = dummyTail->prev->val;
        
        //重新链接
        LinkedNode* backup = dummyTail->prev->prev;
        backup->next = dummyTail;
        //释放该节点空间
        delete dummyTail->prev;
        dummyTail->prev = backup;

        //成功删除，返回
        return key;
    }

    //更新使用状态，将最新使用的节点放在最前方
    void update(int key)
    {
        // //找到key对应的节点
        // LinkedNode* temp = dummyHead;
        // while (temp->next != dummyTail)
        // {
        //     temp = temp->next;
        //     if (temp->val == key)
        //     {
        //         //重新桥接前后两节点
        //         temp->prev->next = temp->next;
        //         temp->next->prev = temp->prev;
        //         //将目标元素放到链表头部
        //         temp->next = dummyHead->next;
        //         temp->prev = dummyHead;
        //         dummyHead->next->prev = temp;
        //         dummyHead->next = temp;
        //         //结束循环
        //         break;
        //     }
        // }

        //使用哈希表进行时间复杂度优化，以空间换时间
        LinkedNode* target = hmap.find(key)->second;
        if (target != nullptr)
        {
            //重新桥接前后两节点
            target->prev->next = target->next;
            target->next->prev = target->prev;
            //将目标元素放到链表头部
            target->next = dummyHead->next;
            target->prev = dummyHead;
            dummyHead->next->prev = target;
            dummyHead->next = target;
        }
    }
};

class LRUCache
{
private:
    int capacity;
    unordered_map<int, int> cache;
    //使用双向链表
    LinkedList lru;

public:
    LRUCache(int cap): capacity(cap) {}
    
    int get(int key)
    {
        if (cache.count(key))
        {
            //更新使用记录
            lru.update(key);
            return cache[key];
        }
        else
            return -1;
    }
    
    void put(int key, int value)
    {
        if (cache.count(key))
        {
            //更新使用记录
            lru.update(key);
            //修改键对应的值
            cache[key] = value;
        }
        else
        {
            if (cache.size() >= capacity)
            {
                //删除最久未使用的节点，并获取其键，将其从哈希表中删除
                cache.erase(lru.erase());
            }
            //初始化使用记录
            lru.add(key);
            //插入新的键值对
            cache[key] = value;
        }
    }
};

困难

K个一组翻转链表

  • 使用一个伪头节点，用首尾夹住$k$个中间被翻转节点的方式，逐$k$个进行翻转与重链接
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

//返回反转后的头部节点（原来的末尾节点）
ListNode* relink(ListNode* l, ListNode* m, ListNode* r, ListNode* end)
{
    m->next = l;
    if (r != end)
        return relink(m, r, r->next, end);
    return m;
}

//从begin到end共k+2个节点，头尾各一个夹着中间需被翻转的部分
void reverse(ListNode* begin, ListNode* end)
{
    //排除无需翻转的情况
    if (begin == end || begin->next == end || begin->next->next == end)
        return;
    
    //记录被翻转部分的初始头节点，即翻转后的尾节点
    ListNode* tail = begin->next;
    //翻转范围内的链表，并与begin和end完成重链接
    begin->next = relink(begin->next, begin->next->next, begin->next->next->next, end);
    tail->next = end;
}

ListNode* reverseKGroup(ListNode* head, int k)
{
    if (head == nullptr) return nullptr;
    if (k == 1) return head;

    ListNode* dummy = new ListNode();
    dummy->next = head;

    //开始扫描
    int count = 0;
    ListNode* iter = dummy;
    ListNode* hook = dummy;
    while (iter->next != nullptr)
    {
        //递增
        count++;
        iter = iter->next;

        //攒够了k个节点，触发翻转
        if (count >= k && count % k == 0)
        {
            //记录被翻转部分链表的原始头部节点，即反转后的尾节点
            ListNode* tail = hook->next;
            //注意hook和iter夹着需要翻转的部分链表
            reverse(hook, iter->next);
            //更新iter的位置到反转后的尾节点上
            iter = tail;
            //更新hook，用于下一轮翻转作为begin传入reverse函数
            hook = iter;
        }
    }

    //由于原head可能被翻转到某处，所以不能直接返回head
    ListNode* ans = dummy->next;
    delete dummy;
    return ans;
}

合并K个升序链表

  • 此题可看作合并两个有序链表的推广，此处参考其思路采用了较为取巧的排序法，时间复杂度较高，但理解起来更简单
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

//注意此处无法对比nullptr，但由于下面在sort前确保移除了空链表，所以无妨
static bool compare(ListNode* l, ListNode* r)
{
    return l->val < r->val;
}

ListNode* mergeKLists(vector<ListNode*>& lists)
{        
    //移除空链表，结合remove_if防止迭代器失效
    auto newEnd = remove_if(lists.begin(), lists.end(), [](ListNode* node) { return node == nullptr; });
    lists.erase(newEnd, lists.end());

    //空则终止
    if (lists.size() == 0)
        return nullptr;

    //按头节点值大小进行排序，取用首位
    sort(lists.begin(), lists.end(), compare);
    ListNode* ans = lists[0];
    lists[0] = ans->next;

    //递归调用
    ans->next = mergeKLists(lists);
    return ans;
}
  • 上述方法中，每次使用sort进行排序其实是不必要的，因为第一次排序后，每轮变化只会改变一个链表元素，不会完全打乱数组，所以我们可以使用二叉堆（优先队列）来优化该点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

//由于priority_queue默认是最大堆，我们需要最小堆，所以此处定义一个相反的比较规则
struct Status
{
    int val;
    ListNode* ptr;
    bool operator<(const Status& rhs) const
    {
        return val > rhs.val;
    }
};

priority_queue<Status> q;

ListNode* mergeKLists(vector<ListNode*>& lists)
{
    //将链表头节点存入优先队列
    for (auto node : lists)
    {
        if (node)
            q.push({node->val, node});
    }

    //构造答案
    ListNode head;
    ListNode* tail = &head;
    while (!q.empty())
    {
        //取出堆顶最小值的链表头
        auto f = q.top();
        q.pop();
        tail->next = f.ptr; 
        tail = tail->next;
        
        //将链表掐头塞回去
        if (f.ptr->next != nullptr)
            q.push({f.ptr->next->val, f.ptr->next});
    }
    return head.next;
}
  • 我们仔细想想就会发觉这一题就是归并排序，类似排序链表引入两两合并链表的子问题后分治地将所有链表合并即可，空间复杂度同样为递归树的$O(\ln n)$，该方法在时间和空间上均不如优先队列的方法，但也是一种不错的思路
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

ListNode* mergeTwoLists(ListNode* list1, ListNode* list2)
{
    if (list1 == nullptr)
        return list2;
    if (list2 == nullptr)
        return list1;

    ListNode dummy;
    ListNode* itr = &dummy;

    while (list1 != nullptr && list2 != nullptr)
    {
        if (list1->val < list2->val)
        {
            itr->next = list1;
            list1 = list1->next;
        }
        else
        {
            itr->next = list2;
            list2 = list2->next;
        }
        itr = itr->next;
    }

    //接上剩余一方的末尾
    itr->next = (list1 == nullptr) ? list2 : list1;
    return dummy.next;
}

ListNode* merge(vector<ListNode*>& lists, int l, int r)
{
    if (l > r)
        return nullptr;
    if (l == r)
        return lists[l];    
    int mid = (r + l) / 2;
    return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));
}

ListNode* mergeKLists(vector<ListNode*>& lists)
{
    //空则终止
    if (lists.size() == 0)
        return nullptr;
    return merge(lists, 0, lists.size() - 1);
}

二叉树

简单

二叉树的中序遍历

  • 递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

void traversal(TreeNode* root, vector<int>& ans)
{
    if (root == nullptr)
        return;

    traversal(root->left, ans);
    ans.emplace_back(root->val);
    traversal(root->right, ans);
}

vector<int> inorderTraversal(TreeNode* root)
{
    vector<int> ans;
    traversal(root, ans);
    return ans;
}

二叉树的最大深度

  • 递归，此处的深度算上了根节点，仅有根节点的树的最大深度即高度为$1$，这与一般定义（仅有根节点的树高度为$0$）有所不同，要注意区分
1
2
3
4
5
6

int maxDepth(TreeNode* root)
{
    if (root == nullptr)
        return 0;
    return 1 + max(maxDepth(root->left), maxDepth(root->right));
}

相同的树

  • 递归
1
2
3
4
5
6
7
8
9
10
11

bool isSameTree(TreeNode* p, TreeNode* q)
{
    if (p == nullptr || q == nullptr)
    {
        if (p == q) return true;
        else return false;
    }

    return (p->val == q->val) &&
    isSameTree(p->left, q->left) && isSameTree(p->right, q->right);        
}

翻转二叉树

  • 递归
1
2
3
4
5
6
7
8
9
10

TreeNode* invertTree(TreeNode* root)
{
    if (root != nullptr)
    {
        std::swap(root->left, root->right);
        invertTree(root->left);
        invertTree(root->right);
    }
    return root;
}

对称二叉树

  • 翻转一个子树，再判断左右子树是否相等
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

bool isEqual(TreeNode* p, TreeNode* q)
{
    if (p == nullptr || q == nullptr)
    {
        if (p == q) return true;
        else return false;
    }

    return (p->val == q->val) &&
    isEqual(p->left, q->left) && isEqual(p->right, q->right);
}

void flip(TreeNode* root)
{
    if (root == nullptr) return;

    swap(root->left, root->right);
    flip(root->left);
    flip(root->right);
}

bool isSymmetric(TreeNode* root)
{
    if (root == nullptr) return true;
    
    flip(root->right);
    return isEqual(root->left, root->right);
}

二叉树的直径

  • 不能直接返回左子树深度与右子树深度之和，因为可能最深的两条路线在同一边子树上
  • 由于计算深度时需要递归对每个子树求解深度，故可在每次求解子树深度的同时维护一个”左子树深度与右子树深度之和”的最大值，最终递归完成时得到的最大值就是答案所求的直径
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

//在计算深度时维护一个答案
int ans;

int maxDepth(TreeNode* root)
{
    if (root == nullptr)
        return 0;
    
    //递归计算深度
    int l = maxDepth(root->left);
    int r = maxDepth(root->right);
    
    //维护答案
    ans = max(ans, l + r);

    //返回深度
    return 1 + max(l, r);
}

int diameterOfBinaryTree(TreeNode* root)
{
    if (root == nullptr)
        return 0;
    if (root->left == nullptr && root->right == nullptr)
        return 0;

    ans = 1;

    //计算深度，函数内部对ans进行维护，每次维护都是对子树直径的一次求解
    maxDepth(root);
    return ans;
}

将有序数组转换为二叉搜索树

  • 选取中点保证平衡，递归创建二叉搜索树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

TreeNode* helper(vector<int>& nums, int left, int right)
{
    if (left > right)
        return nullptr;

    //总是选择中间位置左边的数字作为根节点，以保证平衡
    int mid = (left + right) / 2;

    TreeNode* root = new TreeNode(nums[mid]);
    root->left = helper(nums, left, mid - 1);
    root->right = helper(nums, mid + 1, right);
    return root;
}

TreeNode* sortedArrayToBST(vector<int>& nums)
{
    return helper(nums, 0, nums.size() - 1);
}

中等

验证二叉搜索树

  • 需保证左子树所有节点均小于根节点，右子树所有节点均大于根节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

//帮助检测左子树的最大值是否小于根节点，且右子树的最小值是否大于根节点
bool helper(TreeNode* root, TreeNode* child, bool isLeft)
{
    if (child == nullptr)
        return true;

    if (isLeft)
    {
        while(child->right != nullptr)
            child = child->right;
        return child->val < root->val;
    }
    else
    {
        while(child->left != nullptr)
            child = child->left;
        return child->val > root->val;
    }
}

bool isValidBST(TreeNode* root)
{
    if (root == nullptr)
        return true;
    
    bool l = true, r = true;
    if (root->left != nullptr)
        l = (root->left->val < root->val) && isValidBST(root->left) && helper(root, root->left, 1);
    if (root->right != nullptr)
        r = (root->right->val > root->val) && isValidBST(root->right) && helper(root, root->right, 0);

    return l && r;
}

二叉树的层序遍历

  • 广度优先遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

vector<vector<int>> levelOrder(TreeNode* root)
{
    vector<vector<int>> ret;
    if (root == nullptr)
        return ret;
    
    queue<TreeNode*> q;
    q.push(root);
    
    while (!q.empty())
    {
        int currentLevelSize = q.size();
        ret.push_back(vector<int>());

        for (int i = 1; i <= currentLevelSize; i++)
        {
            TreeNode* node = q.front();
            q.pop();
            ret.back().push_back(node->val);

            if (node->left != nullptr)
                q.push(node->left);
            if (node->right != nullptr)
                q.push(node->right);
        }
    }      
    return ret;
}

二叉搜索树中第K小的元素

  • 对比左子树节点数（依然使用递归求总数）和k的大小关系，递归即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

int getSize(TreeNode* root)
{
    if (root == nullptr)
        return 0;
    return 1 + getSize(root->left) + getSize(root->right);        
}

int getMax(TreeNode* root)
{
    if (root->right == nullptr)
        return root->val;
    return getMax(root->right);
}

int kthSmallest(TreeNode* root, int k)
{
    int l = getSize(root->left);

    if (k < l)
        return kthSmallest(root->left, k);
    else if (k == l)
        return getMax(root->left);
    else if (k == l + 1)
        return root->val;
    else
        return kthSmallest(root->right, k - l - 1);
}

二叉树的右视图

  • 每次递归从头开始遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

//此处的深度算上了根节点，仅有根节点的树的（最大）深度为1，这与一般定义有所不同
int getDepth(TreeNode* root)
{
    if (!root)
        return 0;
    return 1 + max(getDepth(root->left), getDepth(root->right));
}

TreeNode* getRightAtDepth(TreeNode* root, int depth)
{
    //深度为1时就是根节点
    if (depth == 1)
        return root;

    if (getDepth(root->right) >= depth - 1)
        return getRightAtDepth(root->right, depth - 1);
    else
        return getRightAtDepth(root->left, depth - 1);
}

vector<int> rightSideView(TreeNode* root)
{
    if (!root)
        return {};

    vector<int> ans;
    //注意从1开始
    for (int i = 1; i <= getDepth(root); i++)
        ans.emplace_back(getRightAtDepth(root, i)->val);
    return ans;
}
  • 简洁的右侧优先的深度优先搜索
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

vector<int> res;

//从右侧开始的深度优先遍历，传入的u代表递归深度
void dfs(TreeNode *node, int u)
{
    if (u == res.size()) res.push_back(node->val);
    //每次都优先递归右侧子节点，然后再返回来检测左侧
    if (node->right) dfs(node->right, u + 1);
    //然后再返回来递归左侧，最终每层深度上都能找到一个最右侧节点
    if (node->left) dfs(node->left, u + 1);
}

vector<int> rightSideView(TreeNode* root)
{
    if(root) dfs(root, 0);
    return res;
}

二叉树展开为链表

  • 递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

void flatten(TreeNode* root)
{
    if (root == nullptr)
        return;

    //递归扁平化左子树
    flatten(root->left);
    //递归扁平化右子树
    flatten(root->right);

    //暂存右子树（已扁平）
    TreeNode* temp = root->right;
    //将左子树（已扁平）移到右侧
    root->right = root->left;
    root->left = nullptr;
    //将两个已扁平的子树桥接
    TreeNode* tail = root;
    while (tail->right != nullptr)
        tail = tail->right;
    tail->right = temp;
}

从前序与中序遍历序列构造二叉树

  • 对于任意一颗树而言，前序遍历和中序遍历的形式总是如下
1
2

前序：{ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] }
中序：{ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] }
  • 前序遍历中的第一个节点总是根节点，只要我们在中序遍历中定位到根节点，即可分别知道左子树和右子树中的节点数目
  • 继而就可分别知道左右子树的前序遍历和中序遍历结果，即可递归地对构造出左子树和右子树，再将这两颗子树接到根节点的左右位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

TreeNode* helper(vector<int>& preorder, int pl, int pr, vector<int>& inorder, int il, int ir)
{
    int value = preorder[pl];
    TreeNode* root = new TreeNode(value);

    //找到中序遍历数组中的根节点
    int leftTreeSize = 0;
    for (int i = il; i <= ir; i++)
    {
        if (inorder[i] == value)
            leftTreeSize = i - il;
    }

    if (leftTreeSize > 0)
        root->left = helper(preorder, pl + 1, pl + leftTreeSize, inorder, il, il + leftTreeSize - 1);
    if (pr - pl - leftTreeSize > 0)
        root->right = helper(preorder, pl + leftTreeSize + 1, pr, inorder, il + leftTreeSize + 1, ir);

    return root;
}

TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder)
{
    if (preorder.size() == 0)
        return nullptr;

    return helper(preorder, 0, preorder.size() - 1, inorder, 0, inorder.size() - 1);
}

路径总和III

  • 我最开始想到的暴力解法的思路如下
    • 每次对某节点调用helper函数时，其内先会将传入的targetSum值减去节点值，若所得值为0则说明一条路径被发现了，否则继续将该值递归传递下去，若遇到空节点则返回；同时也需要对两个子节点使用原始的originSum值从头开始检测一次
  • 但以下代码存在重复计数的问题
    • 对于测试用例([1,null,2,null,3], 3)而言，会输出3而不是正确的2
      • 节点1
        • 不作累加，helper(root->right, 2)和helper(root->right, 3)
      • 节点2
        • 传入2：累加一次，helper(root->right, 2-2)和==helper(root->right, 3)**
        • 传入3：不作累加，helper(root->right, 3-2)和helper(root->right, 3)
      • 节点3
        • 传入0：不作累加，helper(root->right, 0-3)和helper(root->right, 3)
        • 传入3：累加一次，helper(root->right, 3-3)和helper(root->right, 3)
        • 传入1：不作累加，helper(root->right, 1-3)和helper(root->right, 3)
        • 传入3：累加一次，helper(root->right, 3-3)和helper(root->right, 3)
    • 我们可以发现，上述标黄的部分就是导致重复计数的根源所在，为了修正
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

// int accum = 0;
// int originTarget;

// void helper(TreeNode* root, int targetSum)
// {
//     if (root == nullptr)
//         return;

//     //检查传入目标值是否正好能被消去
//     targetSum -= root->val;
//     if (targetSum == 0)
//         accum++;
    
//     //尝试使用从上一次调用该函数传递进来的目标和
//     helper(root->left, targetSum);
//     helper(root->right, targetSum);

//     //尝试使用原始目标和
//     helper(root->left, originTarget);
//     helper(root->right, originTarget);
// }

// int pathSum(TreeNode* root, int targetSum)
// {
//     //初始化次数，并记录原视目标值
//     accum = 0;
//     originTarget = targetSum;

//     //调用尝试函数，记录累积次数
//     helper(root, originTarget);
//     return accum;
// }
  • 重新审视该暴力思路，我们只需对每个节点调用一个从此节点开始向下逐级对目标和值减去自身节点值的函数，以判断从此身向下延伸是否存在若干路径，然后再分别对左右子树递归地调用一次pathSum，将结果相加即可得到答案
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

//内层递归：计算从当前节点出发的路径数
int countPath(TreeNode* root, int target)
{
    if (!root) return 0;
    
    int count = 0;
    //检查当前节点是否满足目标值
    if (root->val == target) count++;
    
    //继续向子树搜索（目标值更新为剩余值）
    count += countPath(root->left, target - root->val);
    count += countPath(root->right, target - root->val);
    
    return count;
}

//外层递归：遍历所有节点作为路径起点
int pathSum(TreeNode* root, int targetSum)
{
    if (!root) return 0;
    return countPath(root, targetSum)      //计算以当前节点为起点的路径数
        + pathSum(root->left, targetSum)   //递归处理左子树所有节点作为起点
        + pathSum(root->right, targetSum); //递归处理右子树所有节点作为起点
}
  • 前缀和解法的时间与空间复杂度均更优于上述解法
    • 节点的前缀和定义为由根结点到当前结点的路径上所有节点的和
    • 从根节点开始向下深度优先搜索（前序遍历），遍历过程正好形成一条条从根到叶的纵深路径（纵深路径间可能存在重合），我们依次对每条纵深路径进行检验（检查是否存在节点值总和为目标值的子路径）即可
    • 在检测单个节点时，若在当前纵深路径先前检验出的前缀和哈希表中存在元素值与将该节点的前缀和减去目标值相等，那就说明当前节点到哈希表中那个前缀和值对应的节点间的路径长度等于目标值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

//记录当前路径上出现的前缀和以及数量
unordered_map<long long, int> preSumCount;

int dfs(TreeNode* node, int targetSum, long long preSum)
{
    //空节点，满足条件路径数为0
    if(!node) return 0;

    //记录答案
    int pathCnt = 0;

    //更新节点和
    preSum += node->val;
    //从哈希表中获取能和preSum配对的前缀和个数
    pathCnt += preSumCount[preSum - targetSum];                                 
    //然后将当前前缀和加入哈希表
    preSumCount[preSum] += 1;

    //递归处理左右子树
    pathCnt += dfs(node->left, targetSum, preSum);
    pathCnt += dfs(node->right, targetSum, preSum);

    //这个节点所在的路径都处理完了，这个前缀和也就没用了
    preSumCount[preSum] -= 1;
    
    //返回总路径数
    return pathCnt;
}

int pathSum(TreeNode* root, int targetSum)
{
    //有一个默认的前缀和0
    preSumCount[0] = 1;
    //从根节点开始搜索
    return dfs(root, targetSum, 0);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

unordered_map<int, int> prefix;

int subarraySum(vector<int>& nums, int k)
{
    //最开始默认存在1个前缀和0
    prefix[0] = 1;
    
    //记录答案
    int ans = 0;

    //记录累加所得的前缀和
    int accum = 0;
    for (int i = 0; i < nums.size(); i++)
    {
        //累加当前元素
        accum += nums[i];

        //检测当前累计值（即当前元素的前缀和）是否能在哈希表中找到一个前缀和，使得两者之差等于目标值k
        //若能找到，则说明当前元素与哈希表中那个前缀和所对应元素间的子数组长度等于目标值
        ans += prefix[accum - k];

        //然后将当前元素的前缀和加入哈希表
        prefix[accum] += 1;
    }
    return ans;
}

二叉树的最近公共祖先

  • 判断目标是否在左右子树种（isInTree递归查询某节点是否在树内），一旦递归到两个目标分离在左右子树时，此时的根节点即答案
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

bool isInTree(TreeNode* root, TreeNode* target)
{
    if (root == nullptr)
        return false;
    if (root == target)
        return true;

    //深度优先递归搜索目标
    return isInTree(root->left, target) || isInTree(root->right, target);
}

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
{
    if (root == nullptr)
        return nullptr;

    //递归判断目标在左还是右子树
    bool pl = isInTree(root->left, p);
    bool pr = isInTree(root->right, p);
    bool ql = isInTree(root->left, q);
    bool qr = isInTree(root->right, q);

    //两目标节点分别在左右子树，此时根节点即答案
    if (pl && qr)
        return root;
    //否则若两目标全在左侧
    else if (pl && ql)
        return lowestCommonAncestor(root->left, p, q);
    //否则若两目标全在右侧
    else if (pr && qr)
        return lowestCommonAncestor(root->right, p, q);
    //否则根节点一定是某个目标节点，此时返回根节点即可
    else
        return root;
}
  • 以下是另一种递归思路，详见注释
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
{
    if (root == nullptr)
        return nullptr;
    //若根节点是目标，若首调用则根节点就是答案，若非首次调用则相当于遇到目标立刻返回
    if (root == p || root == q)
        return root;

    //递归判断左右子树是否包含任意一目标，返回值可能是目标答案、包含的目标节点、空指针
    TreeNode* left = lowestCommonAncestor(root->left, p, q);
    TreeNode* right = lowestCommonAncestor(root->right, p, q);

    //若left和right都是空，说明此时root中不包含任何目标
    if (left == nullptr && right == nullptr)
        return nullptr;
    //若包含任意目标，则分三种情况讨论，返回根节点答案或其包含的目标是谁
    else
    {
        //若目标分别在左右子树中，则当前节点就是题目答案
        if (left != nullptr && right != nullptr)
            return root;
        //否则左子树中包含目标时，返回左子树的目标是谁
        else if (left != nullptr)
            return left;
        //否则右子树中包含目标时，返回右子树的目标是谁
        else
            return right;
    }
}

二叉搜索树的最近公共祖先

  • 本题用前一题中的方法均可完美通过，但通过搜索树的特性我们可以优化算法复杂度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

bool isInTree(TreeNode* root, TreeNode* target)
{
    if (root == nullptr)
        return false;
    if (root == target)
        return true;

    //以搜索树的特性，更快地查找目标是否存在，而不是像非搜索树那样两边都要递归
    //return isInTree(root->left, target) || isInTree(root->right, target);
    if (target->val > root->val)
        return isInTree(root->right, target);
    else
        return isInTree(root->left, target);
}

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
{
    if (root == nullptr)
        return nullptr;

    //递归判断目标在左还是右子树
    bool pl = isInTree(root->left, p);
    bool pr = isInTree(root->right, p);
    bool ql = isInTree(root->left, q);
    bool qr = isInTree(root->right, q);

    //两目标节点分别在左右子树，此时根节点即答案
    if (pl && qr)
        return root;
    //否则若两目标全在左侧
    else if (pl && ql)
        return lowestCommonAncestor(root->left, p, q);
    //否则若两目标全在右侧
    else if (pr && qr)
        return lowestCommonAncestor(root->right, p, q);
    //否则根节点一定是某个目标节点，此时返回根节点即可
    else
        return root;
}

困难

二叉树中的最大路径和

  • 首先想到的思路是暴力破解，该解法对我来说更容易理解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

int maxSum = INT_MIN;

//以传入结点为起点，向下的最大路径和
int maxGain(TreeNode* root)
{
    if (root == nullptr)
        return 0;

    int accum = 0;
    if (root->val > 0)
    {
        accum += root->val;

        int maxGainFromChild = max(maxGain(root->left), maxGain(root->right));
        if (maxGainFromChild > 0)
            accum += maxGainFromChild;
    }
    else
    {
        int compensate = root->val + max(maxGain(root->left), maxGain(root->right));
        if (compensate > 0)
            accum += compensate;
    }
    return accum;
}

void dfs(TreeNode* root)
{
    if (root == nullptr)
        return;
    
    //获取当前节点向左右延伸的最大路径和
    int sum = root->val;
    int left = maxGain(root->left);
    int right = maxGain(root->right);
    sum += (left > 0) ? left : 0;
    sum += (right > 0) ? right : 0;
    //更新最大答案值
    maxSum = sum > maxSum ? sum : maxSum;

    //递归遍历每个节点
    dfs(root->left);
    dfs(root->right);
}

int maxPathSum(TreeNode* root)
{
    //遍历每个节点
    dfs(root);

    //返回最大值
    return maxSum;
}
  • 我们继续可以把maxGain函数优化掉，就得到了以下解法，时间效率更高
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

int maxSum = INT_MIN;

int dfs(TreeNode* root)
{
    if (root == nullptr)
        return 0;
    
    //从当前节点开始，向左右子树搜索能使自身增长的路径
    int sum = root->val;

    //子树对当前节点的路径长度有贡献时。才会将子树附加
    int left = dfs(root->left);
    int right = dfs(root->right);
    sum += (left > 0) ? left : 0;
    sum += (right > 0) ? right : 0;

    //更新最大值
    maxSum = sum > maxSum ? sum : maxSum;
    
    //返回时不能返回两子树之和，而是只能择其一条，因为返回时是作为单支不分叉的路径
    int bestChildPath = max(left, right);
    return bestChildPath > 0 ? root->val + bestChildPath : root->val;
}

int maxPathSum(TreeNode* root)
{
    //遍历每个节点
    dfs(root);

    //返回最大值
    return maxSum;
}
编程相关, 算法训练
C++
本文由作者按照 CC BY-NC-SA 4.0 进行授权