文章

详解选择排序、插入排序、冒泡排序

先介绍排序算法的定义和研究方法，然后介绍如题所述的三种O(n^2)时间复杂度、O(1)空间复杂度的排序算法，关于其它更快但更耗空间的排序算法参考我的其它博客

发表于
作者 WhythZ
46 分钟阅读
详解选择排序、插入排序、冒泡排序

一、关于排序

1.1 排序的形式

  • 排序（Sorting）就是传入一组线性存储的（可以比较大小的）数据，然后输出一组经过了从大到小或从小到大的顺序排布后的一组数据，输入和输出的数据的元素相同
\[\begin{aligned} \text{Input: }&(a_0,a_1,...,a_{n-1})\\ \text{Output: }&(a_0',a_1',...,a_{n-1}'),\text{ such that }a_0'\leq a_1'\leq...\leq a_{n-1}'\\ \end{aligned}\]
  • 排序算法只能处理有限个固定值的数据，而无法处理无限的或变化的数据
  • 对于结构复杂的数据结构，若想要排序，就一定要给定数据间大小比较的规则，排序规则的不同可能会导致排序结果的不同

复杂数据结构的排序规则不同导致排序结果不同.png

1.2 排序的空间复杂度

  • 排序算法一般被要求最多占用额外的常数级别的$O(1)$内存空间，这被称为In-Place（新手时期的我们排序时总喜欢用额外$O(n)$的内存空间开一个新的数组，这很浪费而低效）
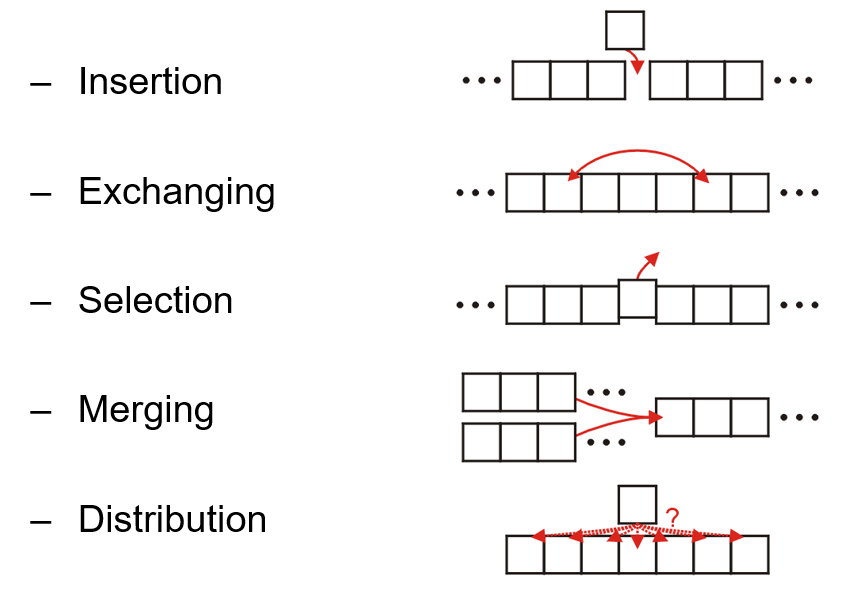
  • 在此基础上，我们能在排序算法中使用的基本操作如下

排序算法中的基本操作.png

1.3 排序的时间复杂度

不存在适用于任何情况的某种最理想的（Optimal）排序算法，我们能依照实际情况选取相对较为优秀的（Sub-Optimal）排序算法

1.3.1 $O(n^2)$

  • 最慢的排序算法，实现简单而直观
\[O(n^2) \text{：Selection Sort, Insertion Sort, Bubble Sort}\]

1.3.2 $O(n\ln(n))$

  • 存储了$n$个数据的线性表有共$n!$种排列方式（Permutation）
  • 一个高度为$h$的完美二叉树的叶节点数为$2^h$，Comparison Tree的每个叶节点存储一种排列方式
  • 所以对于叶节点数为$n!$的Comparison Tree，其高度最小为$h_{min}=\log_{2}{(n!)}$
  • 所以搜索的时间复杂度为$O(h_{min})=O(n\ln(n))$
\[O(n\ln(n)) \text{：Heap Sort, Quick Sort, Merge Sort}\]

1.3.3 $O(n)$

  • 排序算法要遍历完线性表中的每一个元素至少一次，所以时间复杂度最低为$O(n)$而无法更快
\[O(n) \text{：(With Assumption) Bucket Sort, Radix Sort}\]

1.4 逆序对

  • 对于一个含有$n$个数据的列表$(a_0,a_1,…a_{n-1})$，按其从左到右的顺序，存在$\frac{1}{2}A_n^2=\frac{n(n-1)}{2}$对数据
  • 在上述的数据对中，依据这组数据排列的混乱程度的不同，可能会出现若干对脚标相对大小与数据值相对大小关系相反的数据对，其被称为逆序对（Inversion），如下图红色数据对所示
\[(a_i,a_j)\text{ is an inversion if }(i<j)\wedge(a_i>a_j)\]

线性表中的所有数据对例子.png

  • 一般我们认为一组数据的逆序对个数平均为$\frac{1}{2}\cdot(\frac{1}{2}A_n^2)$对，过于偏离这个值的说明其随机度很低

20元素的线性表的逆序对个数.png

二、选择排序

2.1 原理解析

  • 现有一个含$n$个元素的乱序列表，我们遍历找到其中最小的元素，将其与列表中第一位元素（索引为$0$）进行交换，然后继续将剩余部分列表的最小元素通过交换放到索引为$1$处，重复次操作直到最后一次交换后排序完成
  • 下图是选择排序（Selection Sort）进行到中途的情况示意

交换排序.png

2.2 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

//选择排序
//从列表的未排序部分（在最开始，整个列表视为未排序的）中取出最小的值，交换到该部分列表的首位（若首位本来就是最小的，则无需进行Swap操作）
//交换至首位后，该位置的值被纳入整个列表的已排序部分，下次判断操作则从剩余的未排序部分开始
template <typename T>
void SelectionSort(std::vector<T>& _list)
{
    for (size_t i = 0; i < _list.size(); i++)
    {
        //获取列表的未排序部分的最小元素索引
        int _minIdx = i;
        for (size_t j = i + 1; j < _list.size(); j++)
        {
            if (_list[j] < _list[_minIdx])
                _minIdx = j;
        }

        //如果已经是最小的了，则直接跳过该轮循环，无需执行Swap操作
        if (i == _minIdx)
            continue;

        //将未排序部分列表的最小值放到其首（即已排序部分列表的末尾）
        std::swap(_list[i], _list[_minIdx]);
    }
}
  • 该算法的粗略可视化如下所示（此处看不出比较的过程），具体程序参考我的项目仓库
1
2
3
4
5
6
7
8
9
10
11
12
13
14

##LengthOfUnorderedList=15
##SelectionSort
[0]:     14 , 2 , 5 , 12 , 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[1]:    <1>, 2 , 5 , 12 , 3 , 9 , 13 ,<14>, 10 , 15 , 8 , 6 , 7 , 4 , 11
[2]:     1 , 2 ,<3>, 12 ,<5>, 9 , 13 , 14 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[3]:     1 , 2 , 3 ,<4>, 5 , 9 , 13 , 14 , 10 , 15 , 8 , 6 , 7 ,<12>, 11
[4]:     1 , 2 , 3 , 4 , 5 ,<6>, 13 , 14 , 10 , 15 , 8 ,<9>, 7 , 12 , 11
[5]:     1 , 2 , 3 , 4 , 5 , 6 ,<7>, 14 , 10 , 15 , 8 , 9 ,<13>, 12 , 11
[6]:     1 , 2 , 3 , 4 , 5 , 6 , 7 ,<8>, 10 , 15 ,<14>, 9 , 13 , 12 , 11
[7]:     1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 ,<9>, 15 , 14 ,<10>, 13 , 12 , 11
[8]:     1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 ,<10>, 14 ,<15>, 13 , 12 , 11
[9]:     1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 ,<11>, 15 , 13 , 12 ,<14>
[10]:    1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 ,<12>, 13 ,<15>, 14
[11]:    1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 ,<14>,<15>

2.3 复杂度分析

  • 无论是最好还是最坏的情况，该算法每轮都需要进行$O(n)$级别次数的遍历比较操作（以确保在未排序部分列表中找出的值是最小的），时间复杂度始终为$O(n^2)$

三、插入排序

3.1 原理解析

下文讲的是直接插入排序（Direct Insertion Sort），与之对应的还有一种时间效率更优的插入排序叫做希尔排序（Shell Sort）

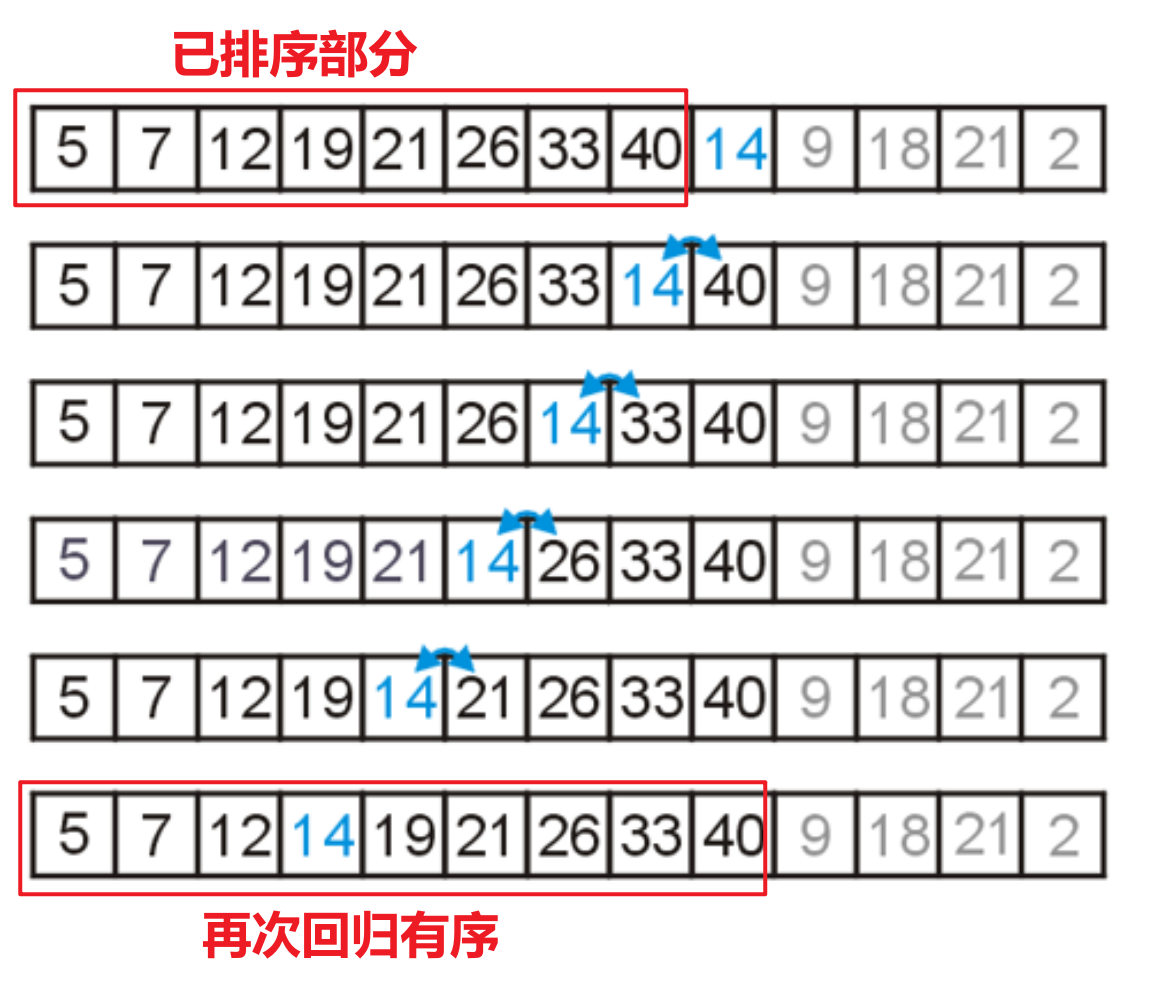
  • 使用该方法进行排序时，我们先从列表的第二个元素开始，将其与前一个元素进行比较，谁小谁放在前面（左侧），确保列表前两个元素保持从左到右递增的顺序
  • 然后对于第三个元素，将其依次与前两元素比较，谁小谁前，确保前三个元素有序，依此类推

插入排序的中间过程示意.png

3.2 代码实现

  • 以下是使用std::swap的方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

//插入排序：
//取出列表索引1处的值，其与0索引值比较，若[1]比[0]大则无需移动，若小则将[1]插入[0]左侧
//然后取出索引2处的值，其与1索引值比较，若[2]比[1]大则无需移动，若小则将其与[0]比较；若[2]比[0]大则将[2]插入[0]右侧、[1]左侧，若小则将[2]插入[0]左侧
//依此类推后续过程，直到遍历至列表中的最后一个元素并完成其判断与可能的移动，排序结束
template <typename T>
void InsertionSort(std::vector<T>& _list)
{
    //注意我们从索引1处开始，因为索引0处的左侧无元素可以比较
    for (size_t i = 1; i < _list.size(); i++)
    {
        //将i索引处的值向左浮动至符合顺序的位置进行"插入"
        size_t _idx = i;
        while (_list[_idx - 1] > _list[_idx])
        {
            std::swap(_list[_idx - 1], _list[_idx]);
            _idx--;
        }
    }
}
  • 该实现的简单可视化如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

##LengthOfUnorderedList=15
##InsertionSort
[0]:     14 , 2 , 5 , 12 , 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[1]:    <2>, 14 , 5 , 12 , 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[2]:     2 ,<5>, 14 , 12 , 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[3]:     2 , 5 ,<12>, 14 , 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[4]:     2 , 5 , 12 ,<3>, 14 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[5]:     2 , 5 ,<3>, 12 , 14 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[6]:     2 ,<3>, 5 , 12 , 14 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[7]:     2 , 3 , 5 , 12 ,<9>, 14 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[8]:     2 , 3 , 5 ,<9>, 12 , 14 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[9]:     2 , 3 , 5 , 9 , 12 ,<13>, 14 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[10]:    2 , 3 , 5 , 9 , 12 , 13 ,<1>, 14 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[11]:    2 , 3 , 5 , 9 , 12 ,<1>, 13 , 14 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[12]:    2 , 3 , 5 , 9 ,<1>, 12 , 13 , 14 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[13]:    2 , 3 , 5 ,<1>, 9 , 12 , 13 , 14 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[14]:    2 , 3 ,<1>, 5 , 9 , 12 , 13 , 14 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[15]:    2 ,<1>, 3 , 5 , 9 , 12 , 13 , 14 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[16]:   <1>, 2 , 3 , 5 , 9 , 12 , 13 , 14 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[17]:    1 , 2 , 3 , 5 , 9 , 12 , 13 ,<10>, 14 , 15 , 8 , 6 , 7 , 4 , 11
[18]:    1 , 2 , 3 , 5 , 9 , 12 ,<10>, 13 , 14 , 15 , 8 , 6 , 7 , 4 , 11
[19]:    1 , 2 , 3 , 5 , 9 ,<10>, 12 , 13 , 14 , 15 , 8 , 6 , 7 , 4 , 11
[20]:    1 , 2 , 3 , 5 , 9 , 10 , 12 , 13 , 14 ,<8>, 15 , 6 , 7 , 4 , 11
[21]:    1 , 2 , 3 , 5 , 9 , 10 , 12 , 13 ,<8>, 14 , 15 , 6 , 7 , 4 , 11
[22]:    1 , 2 , 3 , 5 , 9 , 10 , 12 ,<8>, 13 , 14 , 15 , 6 , 7 , 4 , 11
[23]:    1 , 2 , 3 , 5 , 9 , 10 ,<8>, 12 , 13 , 14 , 15 , 6 , 7 , 4 , 11
[24]:    1 , 2 , 3 , 5 , 9 ,<8>, 10 , 12 , 13 , 14 , 15 , 6 , 7 , 4 , 11
[25]:    1 , 2 , 3 , 5 ,<8>, 9 , 10 , 12 , 13 , 14 , 15 , 6 , 7 , 4 , 11
[26]:    1 , 2 , 3 , 5 , 8 , 9 , 10 , 12 , 13 , 14 ,<6>, 15 , 7 , 4 , 11
[27]:    1 , 2 , 3 , 5 , 8 , 9 , 10 , 12 , 13 ,<6>, 14 , 15 , 7 , 4 , 11
[28]:    1 , 2 , 3 , 5 , 8 , 9 , 10 , 12 ,<6>, 13 , 14 , 15 , 7 , 4 , 11
[29]:    1 , 2 , 3 , 5 , 8 , 9 , 10 ,<6>, 12 , 13 , 14 , 15 , 7 , 4 , 11
[30]:    1 , 2 , 3 , 5 , 8 , 9 ,<6>, 10 , 12 , 13 , 14 , 15 , 7 , 4 , 11
[31]:    1 , 2 , 3 , 5 , 8 ,<6>, 9 , 10 , 12 , 13 , 14 , 15 , 7 , 4 , 11
[32]:    1 , 2 , 3 , 5 ,<6>, 8 , 9 , 10 , 12 , 13 , 14 , 15 , 7 , 4 , 11
[33]:    1 , 2 , 3 , 5 , 6 , 8 , 9 , 10 , 12 , 13 , 14 ,<7>, 15 , 4 , 11
[34]:    1 , 2 , 3 , 5 , 6 , 8 , 9 , 10 , 12 , 13 ,<7>, 14 , 15 , 4 , 11
[35]:    1 , 2 , 3 , 5 , 6 , 8 , 9 , 10 , 12 ,<7>, 13 , 14 , 15 , 4 , 11
[36]:    1 , 2 , 3 , 5 , 6 , 8 , 9 , 10 ,<7>, 12 , 13 , 14 , 15 , 4 , 11
[37]:    1 , 2 , 3 , 5 , 6 , 8 , 9 ,<7>, 10 , 12 , 13 , 14 , 15 , 4 , 11
[38]:    1 , 2 , 3 , 5 , 6 , 8 ,<7>, 9 , 10 , 12 , 13 , 14 , 15 , 4 , 11
[39]:    1 , 2 , 3 , 5 , 6 ,<7>, 8 , 9 , 10 , 12 , 13 , 14 , 15 , 4 , 11
[40]:    1 , 2 , 3 , 5 , 6 , 7 , 8 , 9 , 10 , 12 , 13 , 14 ,<4>, 15 , 11
[41]:    1 , 2 , 3 , 5 , 6 , 7 , 8 , 9 , 10 , 12 , 13 ,<4>, 14 , 15 , 11
[42]:    1 , 2 , 3 , 5 , 6 , 7 , 8 , 9 , 10 , 12 ,<4>, 13 , 14 , 15 , 11
[43]:    1 , 2 , 3 , 5 , 6 , 7 , 8 , 9 , 10 ,<4>, 12 , 13 , 14 , 15 , 11
[44]:    1 , 2 , 3 , 5 , 6 , 7 , 8 , 9 ,<4>, 10 , 12 , 13 , 14 , 15 , 11
[45]:    1 , 2 , 3 , 5 , 6 , 7 , 8 ,<4>, 9 , 10 , 12 , 13 , 14 , 15 , 11
[46]:    1 , 2 , 3 , 5 , 6 , 7 ,<4>, 8 , 9 , 10 , 12 , 13 , 14 , 15 , 11
[47]:    1 , 2 , 3 , 5 , 6 ,<4>, 7 , 8 , 9 , 10 , 12 , 13 , 14 , 15 , 11
[48]:    1 , 2 , 3 , 5 ,<4>, 6 , 7 , 8 , 9 , 10 , 12 , 13 , 14 , 15 , 11
[49]:    1 , 2 , 3 ,<4>, 5 , 6 , 7 , 8 , 9 , 10 , 12 , 13 , 14 , 15 , 11
[50]:    1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 12 , 13 , 14 ,<11>, 15
[51]:    1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 12 , 13 ,<11>, 14 , 15
[52]:    1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 12 ,<11>, 13 , 14 , 15
[53]:    1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 ,<11>, 12 , 13 , 14 , 15

3.3 算法优化

3.3.1 优化掉std::swap

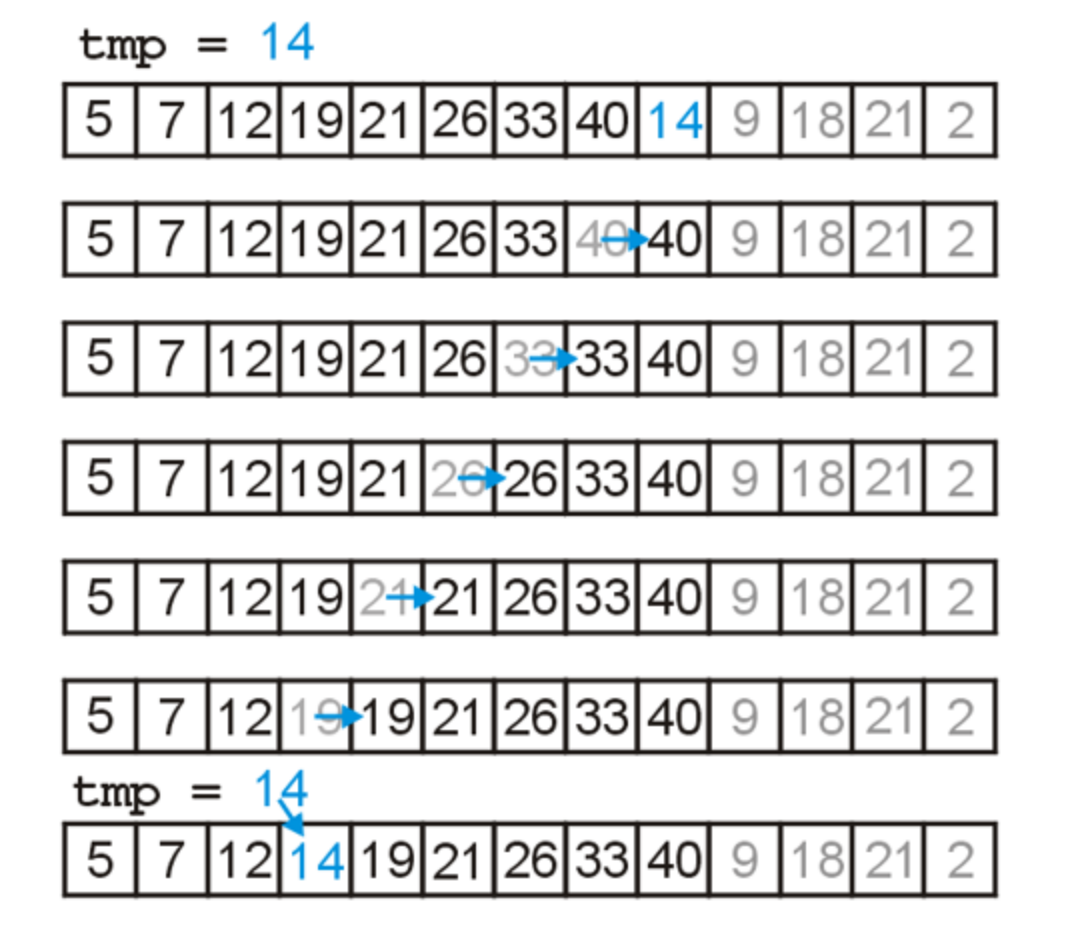
  • 由于频繁使用std::swap的花销相对较大，我们可以将其优化掉，如下图所示

插入排序优化掉swap.png

  • 以下是优化掉std::swap后的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

template <typename T>
void InsertionSort(std::vector<T>& _list)
{
    for (size_t i = 1; i < _list.size(); i++)
    {
        size_t _idx = i;

        //临时存储该值
        T _tmp = _list[i];
		//注意这里是与上述存储的值进行比较
        while (_list[_idx - 1] > _list[_idx])
        {
            _list[_idx] = _list[_idx - 1];
            _idx--;
        }
        //将之前临时存下的值赋值到此处
        _list[_idx] = _tmp;
    }
}

3.3.2 希尔排序

  • 希尔排序（Shell Sort）在使用插入排序之前，先将乱序列表按照相同的间隔拆分为多个子列表，这些子列表的各元素间相隔的元素数量相同
  • 然后分别对这些子列表进行排序，完成一轮后将间隔减半，重新划分子列表，然后继续分组排序
  • 直到间隔为$0$时，就变成了对列表整体进行排序，此时使用插入排序的效率更高，因为前面的步骤将较大的数尽可能地放入了列表的一端，使得插入排序对每个元素进行的比较次数减少

3.4 复杂度分析

  • 直接插入排序算法每次使用std::swap函数时就会纠正一对逆序对（优化掉std::swap后的方法在每次比较进而覆写时的效果是一样的）
    • 对于最坏的情况，逆序对有$\frac{1}{2}A_n^2$对，那么插入排序的时间复杂度就为$O(\frac{1}{2}A_n^2)=O(n^2)$
    • 对于平均的情况，逆序对有$\frac{1}{2}\cdot(\frac{1}{2}A_n^2)$对，时间复杂度仍为$O(n^2)$
    • 对于最优的情况，逆序对的个数为$d=O(n)$，时间复杂度才有可能为$O(n+d)=O(n)$
  • 希尔排序的时间复杂度的数量级是更低的，此处不详细分析，请自行搜索

四、冒泡排序

4.1 原理解析

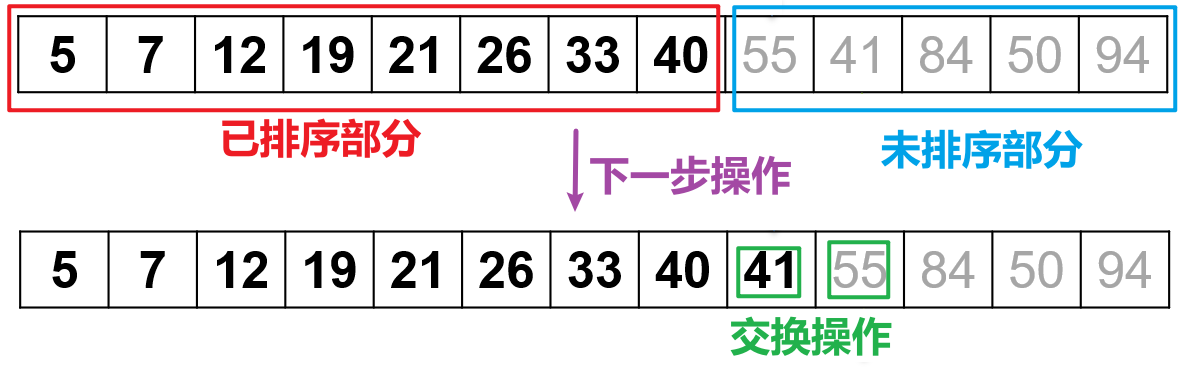
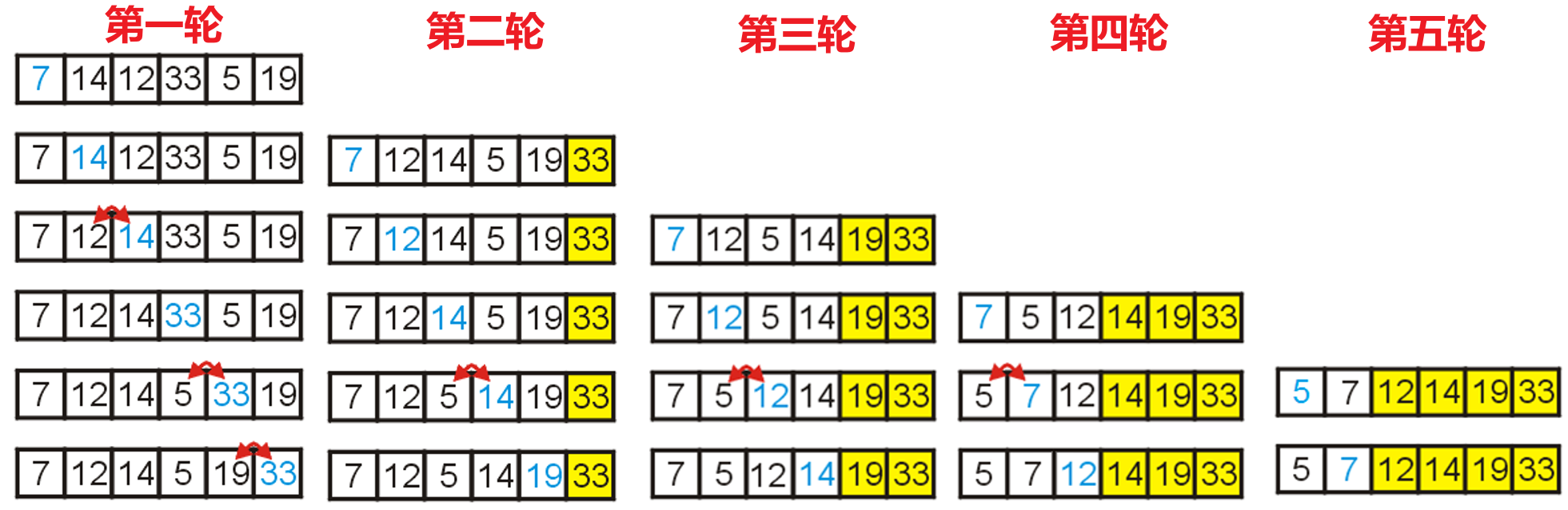
  • 经过第一轮冒泡后，会将最大值冒到列表的末尾，重复$(n-1)$轮后该列表就被从小到大排好了，这就是冒泡排序（Bubble Sort）

冒泡排序图示.png

4.2 代码实现

  • 下面是最基础的冒泡排序实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

//基础的冒泡排序
template <typename T>
void BubbleSort(std::vector<T>& _list)
{
    //外层循环表示要冒(n-1)次泡泡
    for (size_t i = 1; i < _list.size(); i++)
    {
        //内层循环表示要依次对比列表中相邻元素的大小，适时进行交换，共检测(n-1)次
        for (size_t j = 0; j < _list.size() - 1; j++)
        {
            if (_list[j] > _list[j + 1])
            {
                std::swap(_list[j], _list[j + 1]);
            }
        }
    }
}
  • 其效果大致如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

##LengthOfUnorderedList=15
##BubbleSort
[0]:     14 , 2 , 5 , 12 , 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[1]:    <2>,<14>, 5 , 12 , 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[2]:     2 ,<5>,<14>, 12 , 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[3]:     2 , 5 ,<12>,<14>, 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[4]:     2 , 5 , 12 ,<3>,<14>, 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[5]:     2 , 5 , 12 , 3 ,<9>,<14>, 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[6]:     2 , 5 , 12 , 3 , 9 ,<13>,<14>, 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[7]:     2 , 5 , 12 , 3 , 9 , 13 ,<1>,<14>, 10 , 15 , 8 , 6 , 7 , 4 , 11
[8]:     2 , 5 , 12 , 3 , 9 , 13 , 1 ,<10>,<14>, 15 , 8 , 6 , 7 , 4 , 11
[9]:     2 , 5 , 12 , 3 , 9 , 13 , 1 , 10 , 14 ,<8>,<15>, 6 , 7 , 4 , 11
[10]:    2 , 5 , 12 , 3 , 9 , 13 , 1 , 10 , 14 , 8 ,<6>,<15>, 7 , 4 , 11
[11]:    2 , 5 , 12 , 3 , 9 , 13 , 1 , 10 , 14 , 8 , 6 ,<7>,<15>, 4 , 11
[12]:    2 , 5 , 12 , 3 , 9 , 13 , 1 , 10 , 14 , 8 , 6 , 7 ,<4>,<15>, 11
[13]:    2 , 5 , 12 , 3 , 9 , 13 , 1 , 10 , 14 , 8 , 6 , 7 , 4 ,<11>,<15>
[14]:    2 , 5 ,<3>,<12>, 9 , 13 , 1 , 10 , 14 , 8 , 6 , 7 , 4 , 11 , 15
[15]:    2 , 5 , 3 ,<9>,<12>, 13 , 1 , 10 , 14 , 8 , 6 , 7 , 4 , 11 , 15
[16]:    2 , 5 , 3 , 9 , 12 ,<1>,<13>, 10 , 14 , 8 , 6 , 7 , 4 , 11 , 15
[17]:    2 , 5 , 3 , 9 , 12 , 1 ,<10>,<13>, 14 , 8 , 6 , 7 , 4 , 11 , 15
[18]:    2 , 5 , 3 , 9 , 12 , 1 , 10 , 13 ,<8>,<14>, 6 , 7 , 4 , 11 , 15
[19]:    2 , 5 , 3 , 9 , 12 , 1 , 10 , 13 , 8 ,<6>,<14>, 7 , 4 , 11 , 15
[20]:    2 , 5 , 3 , 9 , 12 , 1 , 10 , 13 , 8 , 6 ,<7>,<14>, 4 , 11 , 15
[21]:    2 , 5 , 3 , 9 , 12 , 1 , 10 , 13 , 8 , 6 , 7 ,<4>,<14>, 11 , 15
[22]:    2 , 5 , 3 , 9 , 12 , 1 , 10 , 13 , 8 , 6 , 7 , 4 ,<11>,<14>, 15
[23]:    2 ,<3>,<5>, 9 , 12 , 1 , 10 , 13 , 8 , 6 , 7 , 4 , 11 , 14 , 15
[24]:    2 , 3 , 5 , 9 ,<1>,<12>, 10 , 13 , 8 , 6 , 7 , 4 , 11 , 14 , 15
[25]:    2 , 3 , 5 , 9 , 1 ,<10>,<12>, 13 , 8 , 6 , 7 , 4 , 11 , 14 , 15
[26]:    2 , 3 , 5 , 9 , 1 , 10 , 12 ,<8>,<13>, 6 , 7 , 4 , 11 , 14 , 15
[27]:    2 , 3 , 5 , 9 , 1 , 10 , 12 , 8 ,<6>,<13>, 7 , 4 , 11 , 14 , 15
[28]:    2 , 3 , 5 , 9 , 1 , 10 , 12 , 8 , 6 ,<7>,<13>, 4 , 11 , 14 , 15
[29]:    2 , 3 , 5 , 9 , 1 , 10 , 12 , 8 , 6 , 7 ,<4>,<13>, 11 , 14 , 15
[30]:    2 , 3 , 5 , 9 , 1 , 10 , 12 , 8 , 6 , 7 , 4 ,<11>,<13>, 14 , 15
[31]:    2 , 3 , 5 ,<1>,<9>, 10 , 12 , 8 , 6 , 7 , 4 , 11 , 13 , 14 , 15
[32]:    2 , 3 , 5 , 1 , 9 , 10 ,<8>,<12>, 6 , 7 , 4 , 11 , 13 , 14 , 15
[33]:    2 , 3 , 5 , 1 , 9 , 10 , 8 ,<6>,<12>, 7 , 4 , 11 , 13 , 14 , 15
[34]:    2 , 3 , 5 , 1 , 9 , 10 , 8 , 6 ,<7>,<12>, 4 , 11 , 13 , 14 , 15
[35]:    2 , 3 , 5 , 1 , 9 , 10 , 8 , 6 , 7 ,<4>,<12>, 11 , 13 , 14 , 15
[36]:    2 , 3 , 5 , 1 , 9 , 10 , 8 , 6 , 7 , 4 ,<11>,<12>, 13 , 14 , 15
[37]:    2 , 3 ,<1>,<5>, 9 , 10 , 8 , 6 , 7 , 4 , 11 , 12 , 13 , 14 , 15
[38]:    2 , 3 , 1 , 5 , 9 ,<8>,<10>, 6 , 7 , 4 , 11 , 12 , 13 , 14 , 15
[39]:    2 , 3 , 1 , 5 , 9 , 8 ,<6>,<10>, 7 , 4 , 11 , 12 , 13 , 14 , 15
[40]:    2 , 3 , 1 , 5 , 9 , 8 , 6 ,<7>,<10>, 4 , 11 , 12 , 13 , 14 , 15
[41]:    2 , 3 , 1 , 5 , 9 , 8 , 6 , 7 ,<4>,<10>, 11 , 12 , 13 , 14 , 15
[42]:    2 ,<1>,<3>, 5 , 9 , 8 , 6 , 7 , 4 , 10 , 11 , 12 , 13 , 14 , 15
[43]:    2 , 1 , 3 , 5 ,<8>,<9>, 6 , 7 , 4 , 10 , 11 , 12 , 13 , 14 , 15
[44]:    2 , 1 , 3 , 5 , 8 ,<6>,<9>, 7 , 4 , 10 , 11 , 12 , 13 , 14 , 15
[45]:    2 , 1 , 3 , 5 , 8 , 6 ,<7>,<9>, 4 , 10 , 11 , 12 , 13 , 14 , 15
[46]:    2 , 1 , 3 , 5 , 8 , 6 , 7 ,<4>,<9>, 10 , 11 , 12 , 13 , 14 , 15
[47]:   <1>,<2>, 3 , 5 , 8 , 6 , 7 , 4 , 9 , 10 , 11 , 12 , 13 , 14 , 15
[48]:    1 , 2 , 3 , 5 ,<6>,<8>, 7 , 4 , 9 , 10 , 11 , 12 , 13 , 14 , 15
[49]:    1 , 2 , 3 , 5 , 6 ,<7>,<8>, 4 , 9 , 10 , 11 , 12 , 13 , 14 , 15
[50]:    1 , 2 , 3 , 5 , 6 , 7 ,<4>,<8>, 9 , 10 , 11 , 12 , 13 , 14 , 15
[51]:    1 , 2 , 3 , 5 , 6 ,<4>,<7>, 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
[52]:    1 , 2 , 3 , 5 ,<4>,<6>, 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
[53]:    1 , 2 , 3 ,<4>,<5>, 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15

4.3 算法优化

4.3.1 传统型优化

  • 优化思路：减少大小比较判断（此处不讨论减少std::swap次数的优化思路，因为经过这种优化后的算法已经不太像所谓”冒泡”排序了）
    • 当某轮内部循环未发生std::swap时，则说明该列表已经排列有序，此时就无需继续剩下的循环了，以避免一大批无意义的大小比较的花销
    • 在第$n$轮次的外部循环时，在列表的末尾已经存在排序好的最大的$n$个元素，此部分的元素我们无需对其进行前后的大小比较
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

//优化后的冒泡排序
template <typename T>
void BubbleSort(std::vector<T>& _list)
{
    for (size_t i = 1; i < _list.size(); i++)
    {
        //当内部循环未发生std::swap时，则说明该列表已经排列有序
        bool _isSorted = true;

        //注意此处j<(size-i)，因为每次进行内部循环时，列表末尾已存在排序好的最大的(i-1)个元素
        //此部分的元素无需对其进行前后的大小比较，故我们在原来的j<(size-1)的基础上再减去(i-1)
        for (size_t j = 0; j < _list.size() - i; j++)
        {
            if (_list[j] > _list[j + 1])
            {
                std::swap(_list[j], _list[j + 1]);
                //发生交换则说明需要继续下一轮检测
                _isSorted = false;
            }
        }

        //已经有序的情况下，就无需继续剩下的循环了
        if (_isSorted)
            break;
    }
}
  • 这种优化方式并未改变传统意义上的冒泡排序的过程形式

4.3.2 冒泡+下沉

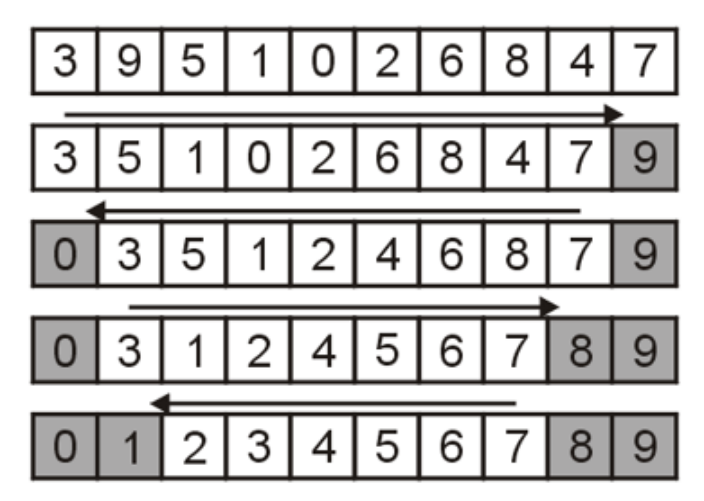
  • 如下图所示，我们可以在将最大值冒泡到列表右侧后，从该点处向左将最小值下沉到列表最左侧，然后我们再在被最大最小值包夹的列表中间部分重复次操作

冒泡+下沉式排序.png

  • 我们需要在程序中使用两个变量记录上下界的索引值，循环重复上述操作，直到上下界相遇，该列表就完成了排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

//冒泡+下沉式的优化排序实现
template <typename T>
void BubbleSort(std::vector<T>& _list)
{
    #pragma region StatesRecord
    //记录初始状态
    _states.EmplaceBack(_list);
    #pragma endregion

    //记录限定列表中间未排序部分的上下界的索引
    size_t _lower = 0;
    size_t _upper = _list.size() - 1;

    //死循环直到排序完成
    while (true)
    {
        //用此时的下界初始化，是为了应对比如{5,1,2,3,4}这种情况
        size_t _newUpper = _lower;
        //将最大值冒泡至列表顶端（右侧）
        for (size_t i = _lower; i < _upper; i++)
        {
            if (_list[i] > _list[i + 1])
            {
                std::swap(_list[i], _list[i + 1]);
                //最后一次发生std::swap的地方一定是新上界处，但不一定等于(_upper-1)
                _newUpper = i;
            }
        }
        //简单地用(_upper-1)来刷新上界可能导致无意义的大小比较
        _upper = _newUpper;

        //同理，用此时的上界初始化
        size_t _newLower = _upper;
        //将最小值下沉至列表底端（左侧），注意此处使用的_upper是已经更新过的上界
        for (size_t i = _upper; i > _lower; i--)
        {
            if (_list[i - 1] > _list[i])
            {
                std::swap(_list[i - 1], _list[i]);
                _newLower = i;
            }
        }
        //同理不能简单地用(_lower+1)更新下界
        _lower = _newLower;

        //比较被刷新过的上下界，若相等，则说明排序完成
        if (_lower == _upper)
            break;
    }
}
  • 该排序过程的简单可视化如下，可以看见一个来回蛇形走动的线，不同于普通的冒泡排序的可视化数图只有向右下方向的的类平行线
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

##LengthOfUnorderedList=15
##BubbleSort
[0]:     14 , 2 , 5 , 12 , 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[1]:    <2>,<14>, 5 , 12 , 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[2]:     2 ,<5>,<14>, 12 , 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[3]:     2 , 5 ,<12>,<14>, 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[4]:     2 , 5 , 12 ,<3>,<14>, 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[5]:     2 , 5 , 12 , 3 ,<9>,<14>, 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[6]:     2 , 5 , 12 , 3 , 9 ,<13>,<14>, 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[7]:     2 , 5 , 12 , 3 , 9 , 13 ,<1>,<14>, 10 , 15 , 8 , 6 , 7 , 4 , 11
[8]:     2 , 5 , 12 , 3 , 9 , 13 , 1 ,<10>,<14>, 15 , 8 , 6 , 7 , 4 , 11
[9]:     2 , 5 , 12 , 3 , 9 , 13 , 1 , 10 , 14 ,<8>,<15>, 6 , 7 , 4 , 11
[10]:    2 , 5 , 12 , 3 , 9 , 13 , 1 , 10 , 14 , 8 ,<6>,<15>, 7 , 4 , 11
[11]:    2 , 5 , 12 , 3 , 9 , 13 , 1 , 10 , 14 , 8 , 6 ,<7>,<15>, 4 , 11
[12]:    2 , 5 , 12 , 3 , 9 , 13 , 1 , 10 , 14 , 8 , 6 , 7 ,<4>,<15>, 11
[13]:    2 , 5 , 12 , 3 , 9 , 13 , 1 , 10 , 14 , 8 , 6 , 7 , 4 ,<11>,<15>
[14]:    2 , 5 , 12 , 3 , 9 , 13 , 1 , 10 , 14 , 8 , 6 , 4 ,<7>,<11>, 15
[15]:    2 , 5 , 12 , 3 , 9 , 13 , 1 , 10 , 14 , 8 , 4 ,<6>,<7>, 11 , 15
[16]:    2 , 5 , 12 , 3 , 9 , 13 , 1 , 10 , 14 , 4 ,<8>,<6>, 7 , 11 , 15
[17]:    2 , 5 , 12 , 3 , 9 , 13 , 1 , 10 , 4 ,<14>,<8>, 6 , 7 , 11 , 15
[18]:    2 , 5 , 12 , 3 , 9 , 13 , 1 , 4 ,<10>,<14>, 8 , 6 , 7 , 11 , 15
[19]:    2 , 5 , 12 , 3 , 9 , 1 ,<13>,<4>, 10 , 14 , 8 , 6 , 7 , 11 , 15
[20]:    2 , 5 , 12 , 3 , 1 ,<9>,<13>, 4 , 10 , 14 , 8 , 6 , 7 , 11 , 15
[21]:    2 , 5 , 12 , 1 ,<3>,<9>, 13 , 4 , 10 , 14 , 8 , 6 , 7 , 11 , 15
[22]:    2 , 5 , 1 ,<12>,<3>, 9 , 13 , 4 , 10 , 14 , 8 , 6 , 7 , 11 , 15
[23]:    2 , 1 ,<5>,<12>, 3 , 9 , 13 , 4 , 10 , 14 , 8 , 6 , 7 , 11 , 15
[24]:    1 ,<2>,<5>, 12 , 3 , 9 , 13 , 4 , 10 , 14 , 8 , 6 , 7 , 11 , 15
[25]:    1 , 2 , 5 ,<3>,<12>, 9 , 13 , 4 , 10 , 14 , 8 , 6 , 7 , 11 , 15
[26]:    1 , 2 , 5 , 3 ,<9>,<12>, 13 , 4 , 10 , 14 , 8 , 6 , 7 , 11 , 15
[27]:    1 , 2 , 5 , 3 , 9 , 12 ,<4>,<13>, 10 , 14 , 8 , 6 , 7 , 11 , 15
[28]:    1 , 2 , 5 , 3 , 9 , 12 , 4 ,<10>,<13>, 14 , 8 , 6 , 7 , 11 , 15
[29]:    1 , 2 , 5 , 3 , 9 , 12 , 4 , 10 , 13 ,<8>,<14>, 6 , 7 , 11 , 15
[30]:    1 , 2 , 5 , 3 , 9 , 12 , 4 , 10 , 13 , 8 ,<6>,<14>, 7 , 11 , 15
[31]:    1 , 2 , 5 , 3 , 9 , 12 , 4 , 10 , 13 , 8 , 6 ,<7>,<14>, 11 , 15
[32]:    1 , 2 , 5 , 3 , 9 , 12 , 4 , 10 , 13 , 8 , 6 , 7 ,<11>,<14>, 15
[33]:    1 , 2 , 5 , 3 , 9 , 12 , 4 , 10 , 13 , 6 ,<8>,<7>, 11 , 14 , 15
[34]:    1 , 2 , 5 , 3 , 9 , 12 , 4 , 10 , 6 ,<13>,<8>, 7 , 11 , 14 , 15
[35]:    1 , 2 , 5 , 3 , 9 , 12 , 4 , 6 ,<10>,<13>, 8 , 7 , 11 , 14 , 15
[36]:    1 , 2 , 5 , 3 , 9 , 4 ,<12>,<6>, 10 , 13 , 8 , 7 , 11 , 14 , 15
[37]:    1 , 2 , 5 , 3 , 4 ,<9>,<12>, 6 , 10 , 13 , 8 , 7 , 11 , 14 , 15
[38]:    1 , 2 , 3 ,<5>,<4>, 9 , 12 , 6 , 10 , 13 , 8 , 7 , 11 , 14 , 15
[39]:    1 , 2 , 3 ,<4>,<5>, 9 , 12 , 6 , 10 , 13 , 8 , 7 , 11 , 14 , 15
[40]:    1 , 2 , 3 , 4 , 5 , 9 ,<6>,<12>, 10 , 13 , 8 , 7 , 11 , 14 , 15
[41]:    1 , 2 , 3 , 4 , 5 , 9 , 6 ,<10>,<12>, 13 , 8 , 7 , 11 , 14 , 15
[42]:    1 , 2 , 3 , 4 , 5 , 9 , 6 , 10 , 12 ,<8>,<13>, 7 , 11 , 14 , 15
[43]:    1 , 2 , 3 , 4 , 5 , 9 , 6 , 10 , 12 , 8 ,<7>,<13>, 11 , 14 , 15
[44]:    1 , 2 , 3 , 4 , 5 , 9 , 6 , 10 , 12 , 8 , 7 ,<11>,<13>, 14 , 15
[45]:    1 , 2 , 3 , 4 , 5 , 9 , 6 , 10 , 12 , 7 ,<8>,<11>, 13 , 14 , 15
[46]:    1 , 2 , 3 , 4 , 5 , 9 , 6 , 10 , 7 ,<12>,<8>, 11 , 13 , 14 , 15
[47]:    1 , 2 , 3 , 4 , 5 , 9 , 6 , 7 ,<10>,<12>, 8 , 11 , 13 , 14 , 15
[48]:    1 , 2 , 3 , 4 , 5 , 6 ,<9>,<7>, 10 , 12 , 8 , 11 , 13 , 14 , 15
[49]:    1 , 2 , 3 , 4 , 5 , 6 ,<7>,<9>, 10 , 12 , 8 , 11 , 13 , 14 , 15
[50]:    1 , 2 , 3 , 4 , 5 , 6 , 7 , 9 , 10 ,<8>,<12>, 11 , 13 , 14 , 15
[51]:    1 , 2 , 3 , 4 , 5 , 6 , 7 , 9 , 10 , 8 ,<11>,<12>, 13 , 14 , 15
[52]:    1 , 2 , 3 , 4 , 5 , 6 , 7 , 9 , 8 ,<10>,<11>, 12 , 13 , 14 , 15
[53]:    1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 ,<9>,<10>, 11 , 12 , 13 , 14 , 15

4.3.3 对比插入排序

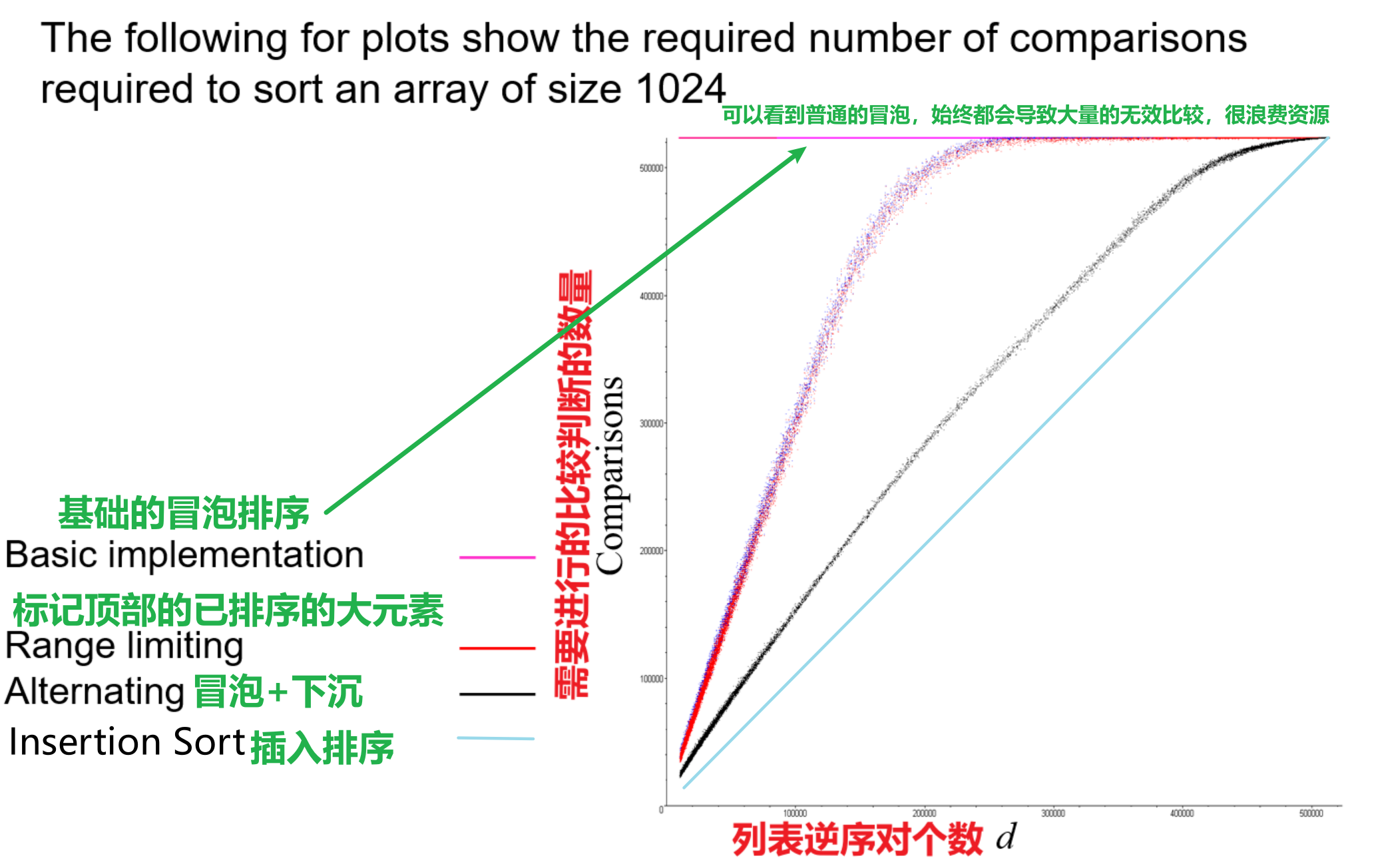
  • 冒泡排序中存在的无意义比较操作是导致其复杂度高的根本原因，即便优化到此地步，还是比不上插入排序的效率

冒泡排序中的无效比较示意图.png

4.4 复杂度分析

  • 对于普通的冒泡排序，其复杂度始终为$O(n^2)$
  • 对于我们优化过后的冒泡+下沉排序（注意其中$\omega(n)$指最优复杂度为$n$，即下界；而$O(n)$指最坏的复杂度为$n$，即上界）
    • 最坏情况，时间复杂度为$O(n^2)$，逆序对个数为$d=O(n^2)$
    • 平均情况，时间复杂度为$O(n+d)$，但逆序对个数为$d=\omega(n)$时会很慢
    • 最优情况，时间复杂度为$O(n)$，逆序对个数为$d=O(n)$
学科笔记, 数据结构
数据结构 C++
本文由作者按照 CC BY-NC-SA 4.0 进行授权