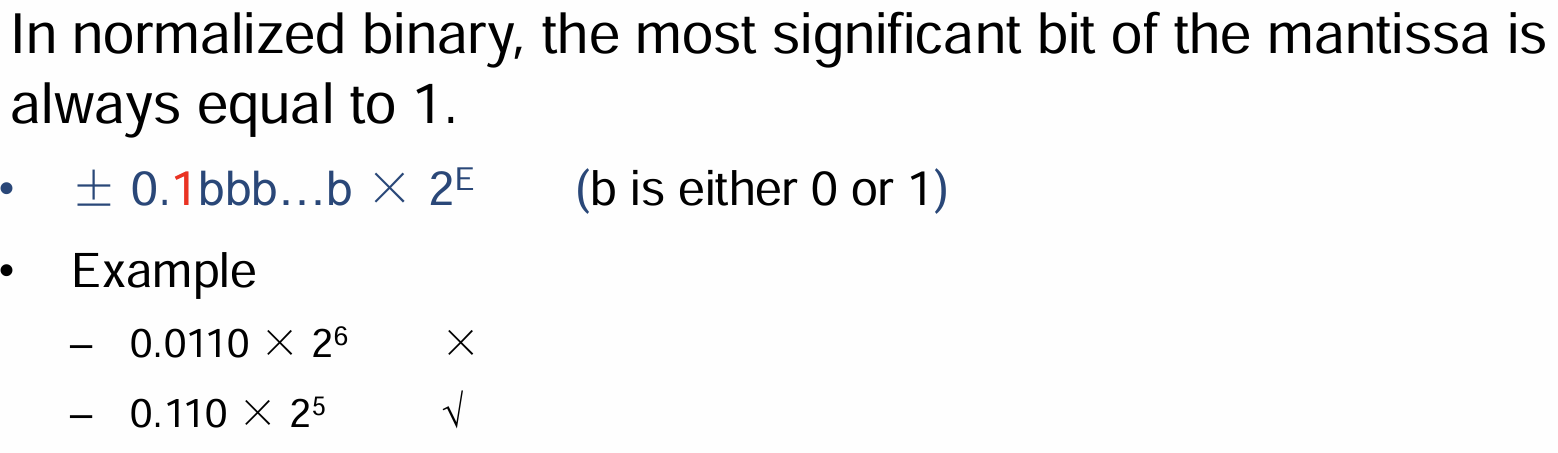计算机中的IEEE754浮点数

一、定点数表示

• 定点数（Fixed-Point Number）的小数点位置固定不变的，定义写的是小数点（Binary Point）右侧的小数位（Number Of Bits）不变，有点拗口
• 对于无符号或有符号整型数的定点数表示，小数点的右侧没有任何数位
• 对于有符号的分数（Fraction），小数点需要表示出来，但注意小数点必须在符号位的右侧

• 注意上图中对于这样一个$(n+1)$位补码表示的数的范围区间，参考整数的补码表示相关内容
• 这种表示的缺点就是无法表示过大的数

二、浮点数表示

2.1 基本介绍

• 浮点数（Floating-Point Number）的小数点的位置是可变的
• 如下图，$S$代表符号位，$E$代表浮点数的整数部分，$M$（Mantissa, 尾数）代表小数部分，即$M$为一个小于$1$的分数（Fraction），小写$e$带入该式子表示是该数的真值，而大写$E$则是将该数变为移码（全部为正），方便比较

• 这种表示形式类比十进制的科学计数法（$\overline{x.xx} \cdot 10^n$），只有$M$是二进制的表示，其余两部分一个是表示符号，一个是表示数量级，数量级的底用十进制的$2$而不是二进制的$10$表示，我猜测应该是怕搞混

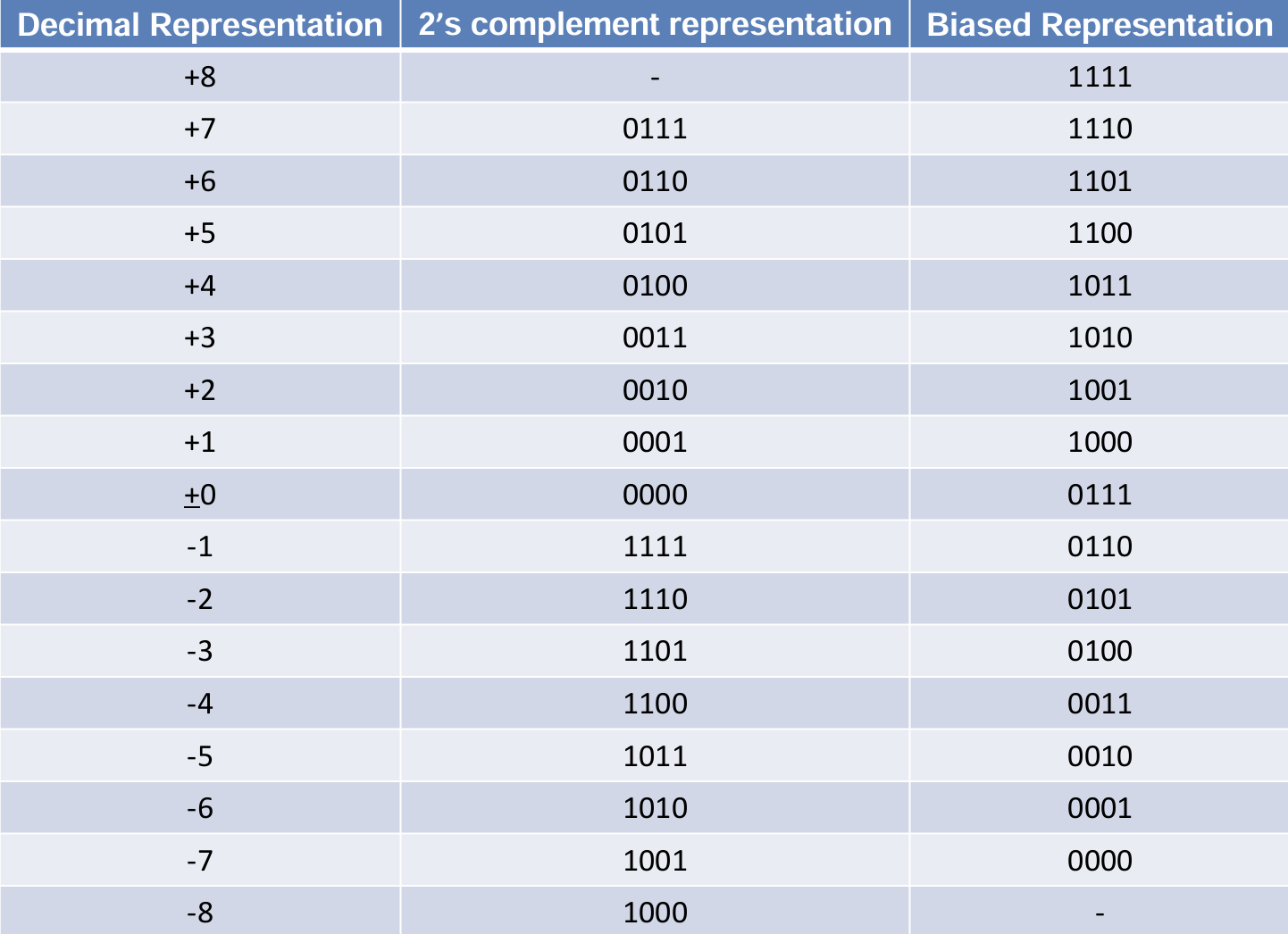
2.2 移码

• 两个除了指数外都相同的浮点数（$x.xxx \cdot 2^a$、$x.xxx \cdot 2^b$）间可以通过比较指数的阶数来简化大小比较的过程，但是若指数$a=-1$，$b=1$的话，那么计算机会在没有比较器的帮助下，使用补码进行简单的比较而得出错误的比较结果

• 为了使得浮点数的指数以无符号形式表示，我们在原数的基础上增加一个偏移量（Biased/Excess Notation）将浮点数表示为移码形式用来表示浮点数的阶码，其中$e$为真值，$k$为整数真值的位数

\[E=[e]_移=e + (2^{k-1} - 1)\]

• 移码只是把二进制码的某一个数（下图中是$-7=1001_补$）设定为数字 0，将数字整体平移出现的，这样可以保证负数在二进制码下的大小关系和实际的大小关系相同

• 移码和补码有一个很简洁的关系：将移码的符号位取反，再在末位$+1$，数值与原来相同，出现这个关系的条件是：数字的偏移量必须是$2^{n−1}$（二进制码最大值的一半）

2.3 标准化

• 下图展示了什么是标准化（或规格化）的（Normalized）浮点数，负数同理

• 二进制的标准化如下，符号位不包含在内（正负号写在数的前面），小数点前的0无意义，相当于是类比十进制的小数形式

2.4 IEEE754标准

计算机必须要支持单精度浮点数表示以符合IEEE754标准，双精度则可选可不选

2.4.1 单精度与双精度浮点数

• 该标准规定的单精度（32bits）浮点数表示规范如下图所示
  • $S$表示符号位
  • $E$减去偏移量表示该浮点数真值的$2$的指数$e$，$E$（始终为正）的作用就是用于比较大小的
  • $M$即以原码表示的尾数
  • $X = (-1)^S2^(E)$
• $E$和$M$都不为$0$时表示正常的数；当$E$为$0$且$M$不为0时表示$NaN$；当二者都为$0$时表示$0$；当E不为$0$且$M$为$0$时表示无穷
• 注意该类浮点数所能表示的数的绝对值大小范围（说明可正可负），其推导范围详见图中注释

• 双精度（64bits）浮点数规范如下，取值范围的计算同理

• 注意上面的$M$部分是$23$或$52$位，不包括$1.M$中小数点的左侧那个$1$，所以其中$1.M$的取值范围是十进制表示的$[1,2)$，永远不能等于$2$，$1.M$的最大值就是$[1.11..1]2 = [2]{10} - [0.00..1]_2$

2.4.2 特殊值的表示

• 当E为0且M不为0时，表示NaN；当二者都为0时，表示0；当E不为0且M为0时，表示无穷
• 下面的都是规定，不要深究

• 对于非标准化的数，即在十进制的$(-0.5,0)\cup(0,+0.5)$范围内的数，因为标准化的数（即$0.1bbbbbb$形式的数，$b$为$0$或$1$）能表示的最小的两个正数分别是二进制的$0.0\cdot2^0$与$0.1\cdot2^0$，即十进制的$0$与$\frac{2^0}{2^1}=0.5$，所以在这两个数之间的数是无法用标准化的形式表示的，对于负数同理，所以这两个区间内的数称为非标准化（Denormal）的数

三、浮点数的运算

3.1 对齐与加减法

• 进行浮点数加减时，第一步是要将二者进行相互的指数对齐（Alignment）
• 如下图，红色是指数小的向大的对齐，小的那个的非指数部分数的小数点左移了（尾数右移），对于计算机来说这样会丢失尾巴部分的低位数位，对精度的影响较小；而黑色是将指数大的向小的对齐，使得对应的数小数点右移（尾数左移），这样会导致计算机丢失高位数位，这样对精度的影响巨大

• 所以第一步：我们应当让指数小的向指数大的对齐
• 然后第二步：对齐后进行尾数（Mantissas）的相加减的运算
• 最后第三步：如果需要的话，将数的表示标准化（Normalize）

3.2 乘法

• 以IEEE 754标准的单精度浮点数$(-1)^S2^{E-127}(1.M)$为例
  • 第一步：确定符号，并将两数的指数相加
  • 第二步：将两数的尾数$M$相乘，得到的积即为长度增长的的新尾数$M’$
  • 第三步：如果需要的话，将结果进行标准化

3.3 除法

• 以IEEE 754标准的单精度浮点数$(-1)^S2^{E-127}(1.M)$为例
  • 第一步：确定符号，并将两数的指数相减
  • 第二步：将两数的尾数$M$相除，得到的商即为长度减少的新尾数$M’$
  • 第三步：如果需要的话，将结果进行标准化

四、浮点数运算精度问题

4.1 保护位

• 在浮点数的运算中，结果的尾数长度可能会超出原数的尾数位数，保护位（Guard Bits）就是用于存储这些位上的数的，其会被用于填充到原数尾数的末端
• 例如在加减法运算中，当我们把相对小的数向上对齐的时候，其尾部数位会丢失若干位（等于指数之差），保护位则用于保存这些丢失的位，以保证浮点数运算的精度

4.2 保护位的舍入

4.2.1 介绍

• 由于尾数$M$是有位数限制的（单精度$23$/双精度$52$），而在运算过程中可能会导致结果的尾数长度超出这个限制，此时就需要对尾数进行舍入（Truncation），即以某种方式丢弃（Discard）多余的位，舍入后才可对结果浮点数进行保存
• 截断应当是无偏的（Unbiased）最好
• 先要了解两个概念
  • MSB（Most Significant Bit）：最高有效位，二进制中代表最高值的比特位，这一位对数值的影响最大
  • LSB（Least Significant Bit）：最低有效位，二进制中代表最低值的比特位。

4.2.2 Chopping

截断法，不是最佳（Optimum）的方法，因其是有偏的

• 直接将保护位删除，不对计算结果现有的位做任何改变
• 此方法的好处是容易实现，但却是有偏（Biased）的，因为所有的值都向较小的尾数值舍入了
• 此方法的误差范围为$[0,1)$，例如将$0.b_1b_2b_3x_1x_2x_3$的尾数只保留三位（即留下$0.b_1b_2b_3$），那么就会丢失$0.000x_1x_2x_3$这个数，则此次Chpping造成的误差范围就在$[0,0.000111]$范围内

4.2.3 Von Neumann Rounding

冯诺依曼舍入法，又称置一法，无偏

• 如果被舍去的位均为$0$，那么就直接舍去，比如将；如果舍去的位中存在一个$1$，则将该二进制数的最低有效位（LSB）设为$1$
• 例如保留$0.b_1b_2b_3x_1x_2x_3$的三位小数，$0.b_1b_2b_3000$就会变为$0.b_1b_2b_3$；而在$[0.b_1b_2b_3 001,0.b_1b_2b_3 111]$之间的数，则都保留为$0.b_1b_2 1$，若$b_3$为$0$，则这样舍入就会造成$(0.b_1b_2 1 - 0.b_1b_2 0 x_1x_2x_3)$的正误差，若$b_3$为$1$，则这样会导致原本$b_3$后的小数被丢掉，造成了$(0.b_1b_2 1 x_1x_2x_3 - 0.b_1b_2 1)$的负误差
• 所以此方法的偏差范围在$(-1,1)$范围内，关于$0$对称，所以这种方法是无偏的

4.2.4 Rounding

零舍一入法，无偏，且偏差要比冯诺依曼舍入的小，这是IEEE标准浮点数默认的舍入方法

• 该方法类似四舍五入，区别在于对所谓”5”的处理，其误差范围中的$\frac{1}{2}$也源自于此；规则详见下图

• 其偏差范围在$(-\frac{1}{2},\frac{1}{2})$范围内，故无偏

4.3 规格化

4.4 溢出

• IEEE浮点数计算过程中难免会产生一些超出IEEE规范表示范围的浮点数结果
• 指数的溢出

• 尾数的溢出（不是真正的溢出，因为其溢出可以被解决，而指数的溢出无法被解决）

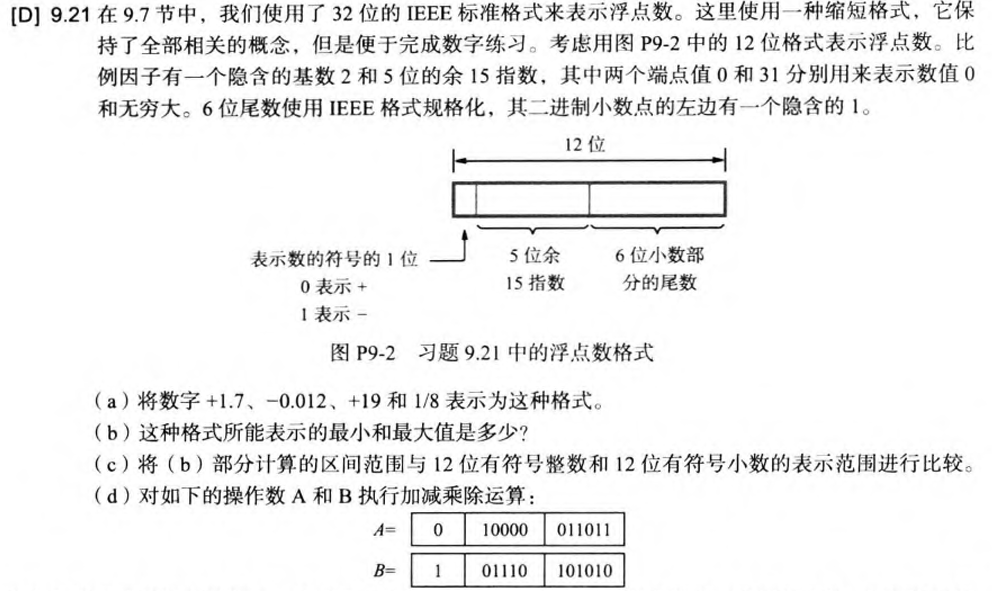
五、习题训练

• 先搞清楚如何将十进制转化为小数形式，然后再看下面的题目

• 上面那题我给出了详细的注释，下面还有两道例题，可以自己试着做一做