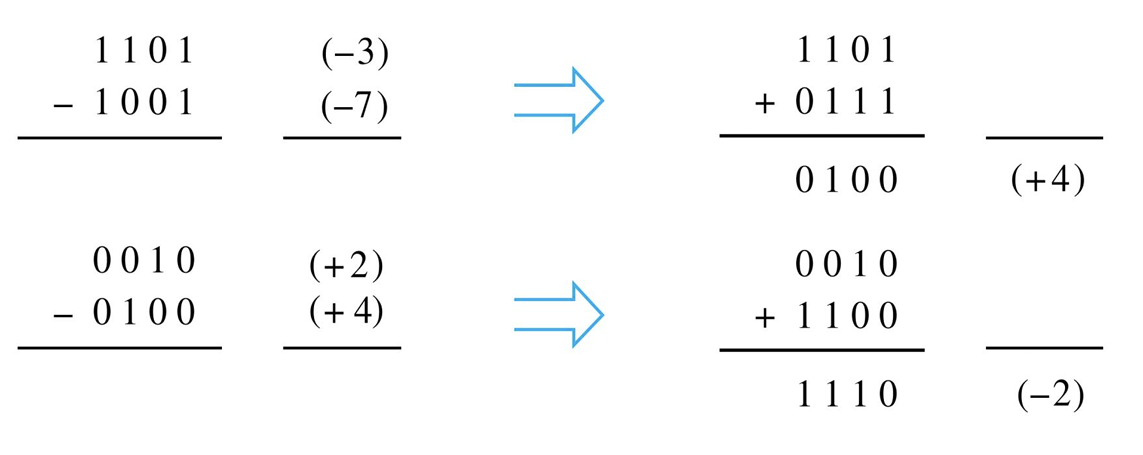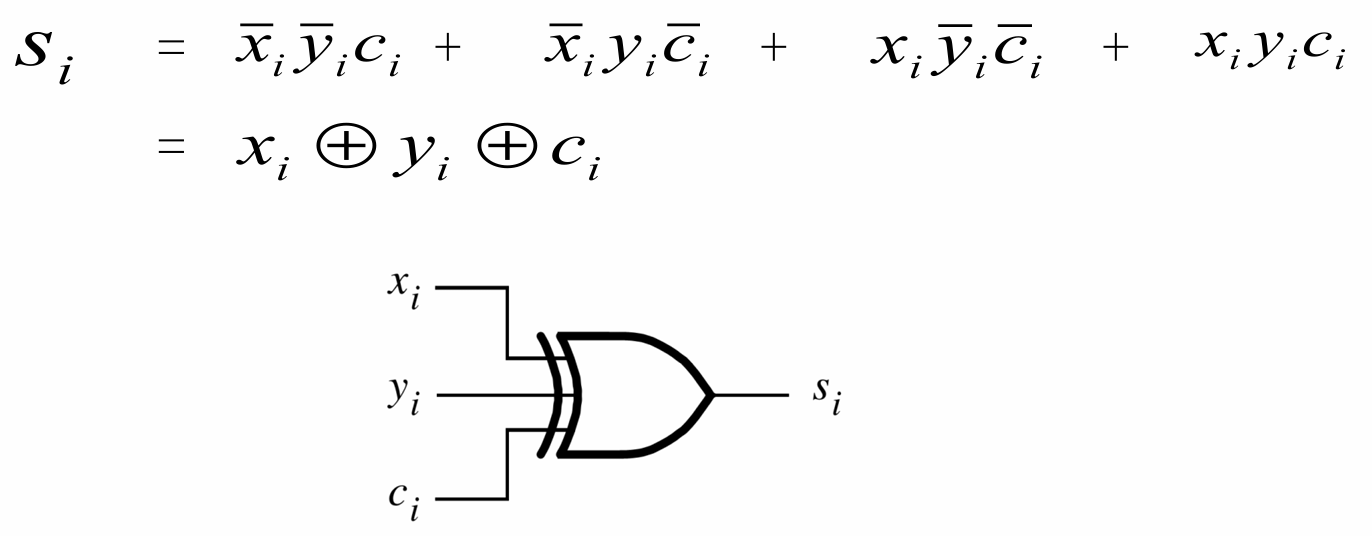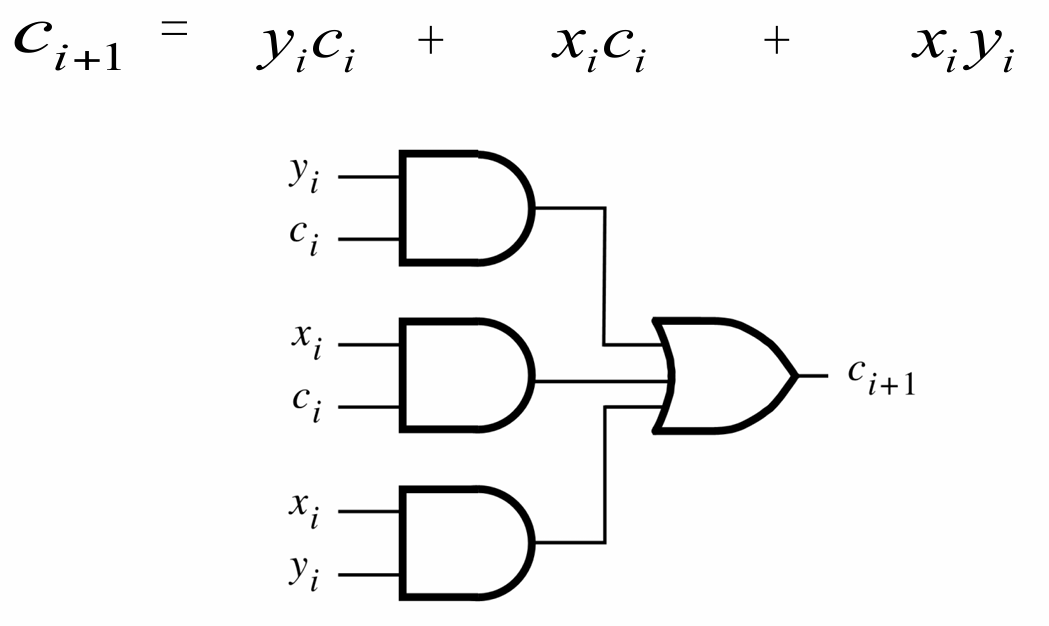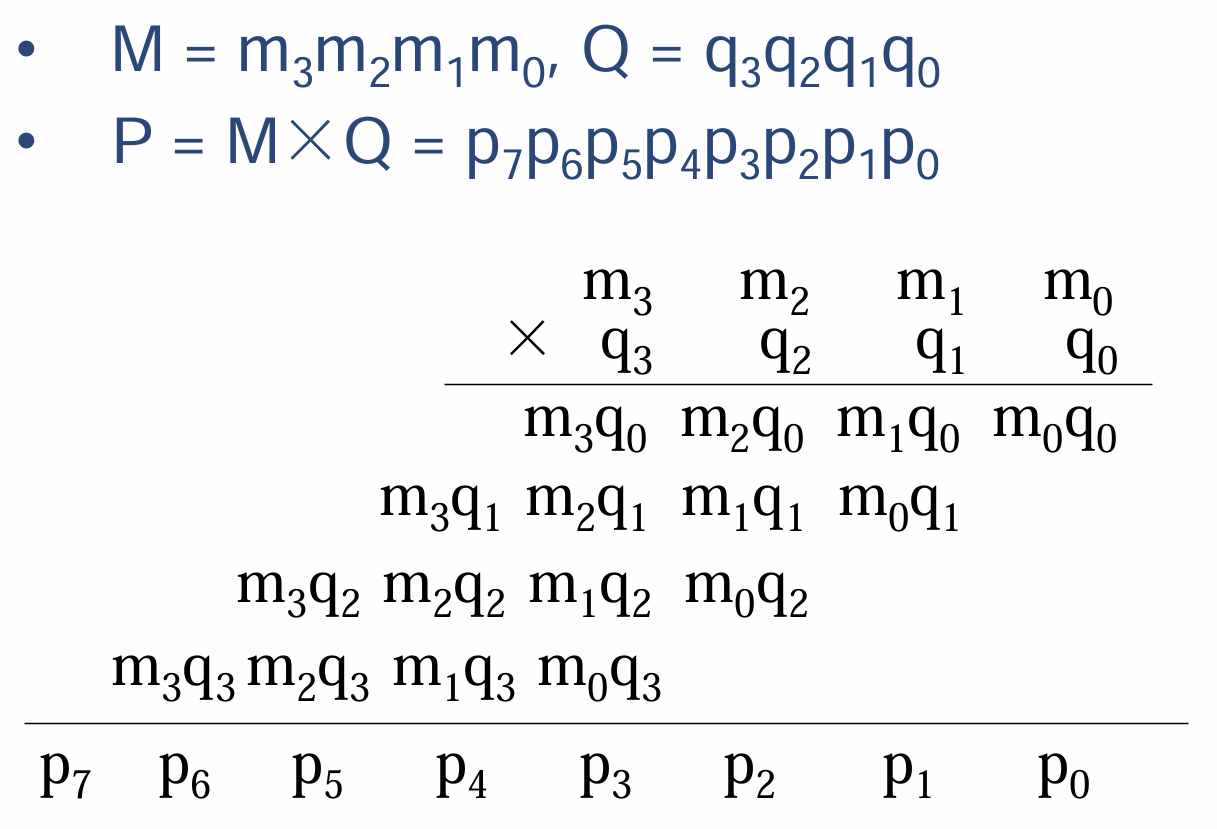文章

计算机中的整数及其四则运算

大二学习计算机组成原理课程时记录的整数相关笔记，重点解析整数的加法、乘法、除法的原理及其硬件实现逻辑

发表于 更新于
作者 WhythZ
30 分钟阅读
计算机中的整数及其四则运算

一、整数的表示

1.1 二进制

  • 一个无符号的n位（n-bit）的二进制整数表示，$b_i$取0或1
\[\overline{b_{n-1}...b_1b_0}\]
  • 这个数的十进制值为
\[B=\sum_{i=0}^{n}{b_i \cdot 2^{i}}\]

1.2 原码

原码（Sign and Magnitude）的加法和减法是分开考虑的，这不好

  • 原码：对于一个n位的整数，最左边的一位数是符号位（0正1负），剩下的n-1位表示该整数的绝对值大小，称为真值

计算机有符号二进制整数.png

  • 这种方式表示的数的范围是$[-(2^{n-1}-1),2^{n-1}-1]$
  • 这种表示方法的缺点是0这个数有两种表示，并且加减的时候需要同时考虑大小和符号

1.3 反码

反码（1’s Complement）可以只保留加法，减去某个数即加上负数，这样得到的补码结果转换为原码后，其真值是正确的，但是会发现0这个数还是有两种表示方式

  • 反码：正数的反码是其本身，负数的反码是在其原码的基础上符号位不变，其余各个位按位取反（Bitwise Complement），即0变1，1变0
\[\begin{aligned} +1 = [0000 0001]原= [0000 0001]反 \\ -1 = [1000 0001]原= [1111 1110]反 \end{aligned}\]

1.4 补码

补码（2’s Complement）不仅可以用加法覆盖减法，也解决了0的两个编码问题

  • 补码：正数的补码就是其本身，负数的补码是在其原码的基础上符号位不变，其余各位取反，并在最后一位上+1，也即在反码的基础上+1（若最后一位已经为1，则需要进位）
\[\begin{aligned} +1 = [0000\space0001]原= [0000\space0001]反= [0000\space0001]补 \\ -1 = [1000\space0001]原= [1111\space1110]反= [1111\space1111]补 \end{aligned}\]
  • 观察使用补码进行$1+(-1)$的运算，结果为[1 0000 0000]补，由于8bit表示会省去多出来的这个进位，所以这样实际得到的数是[0000 0000]补，这样的0就只有一种表示方法了，而多出来的[1000 0000]补就可以多表示一个负数，对于8bit的数，原码表示的范围为$[-127, 127]$，而补码表示的范围就是$[-128, 127]$，所以$n$位补码表示整数的范围为$[-(2^{n-1}),2^{n-1}-1]$

1.5 不同位间的转换

  • 原码8bit和16bit间的转换

原码8转16.png

  • 补码8bit和16bit间的转换，注意到对于负数的补码的转换是有问题的，所以我们可知，补码从8bit转换到16bit需要用符号数0或者1来填补空位

![补码8与16.ng

\[\begin{aligned} -18 &= \phantom{000000000}1110\space1110 \text{ (8bit)} \\ -18 &= 1111\space1111\space1110\space1110 \text{ (16bit)} \end{aligned}\]

二、行波进位加法器

2.1 二进制加减

此处进行的是补码的加减

2.1.1 加法

  • 两个相加的数需是相同位数的补码形式，符号位也被纳入计算
  • 从最右侧开始相加，逢二进一，和十进制的竖式计算一样存在进位（Carry-Out）
  • 符号位的进位被忽略，加法的结果是和两个加数相同位数的

2.1.2 减法

  • $(A-B)$等同于$(A+(-B))$，所以本质上还是做加法，问题就转换为如何将某个数的符号取反
  • 将一个补码数转化为与其符号相反的数的补码（Negation Operation），等同于将这个数的包括符号位的所有位全部取反后加上00..01

补码的减法即转化为加法.png

2.1.3 溢出

  • 两个合法的相同符号的数相加，若结果符号与两加数不同，则产生了溢出（Overflow）
  • 符号相反的数相加，结果的绝对值只会比两个加数中绝对值最大的数小，不可能溢出

2.2 全加器实现1-bit加法

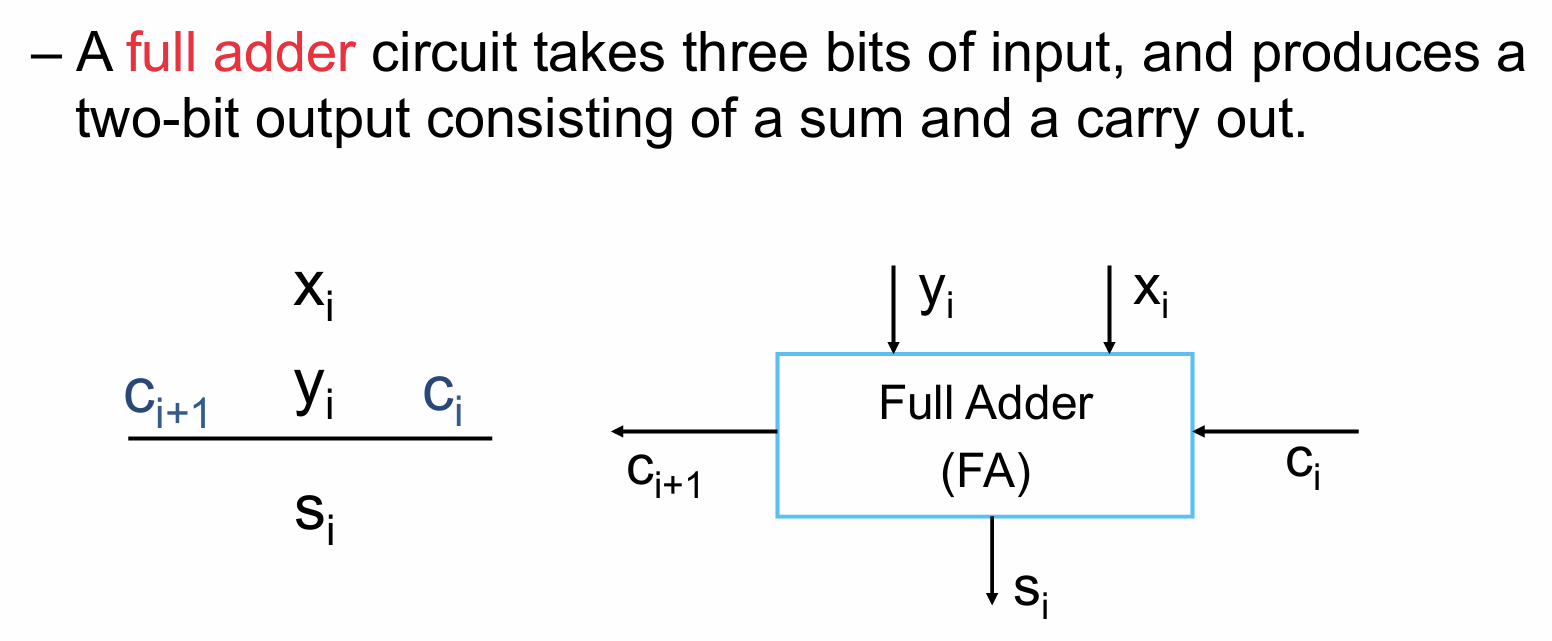
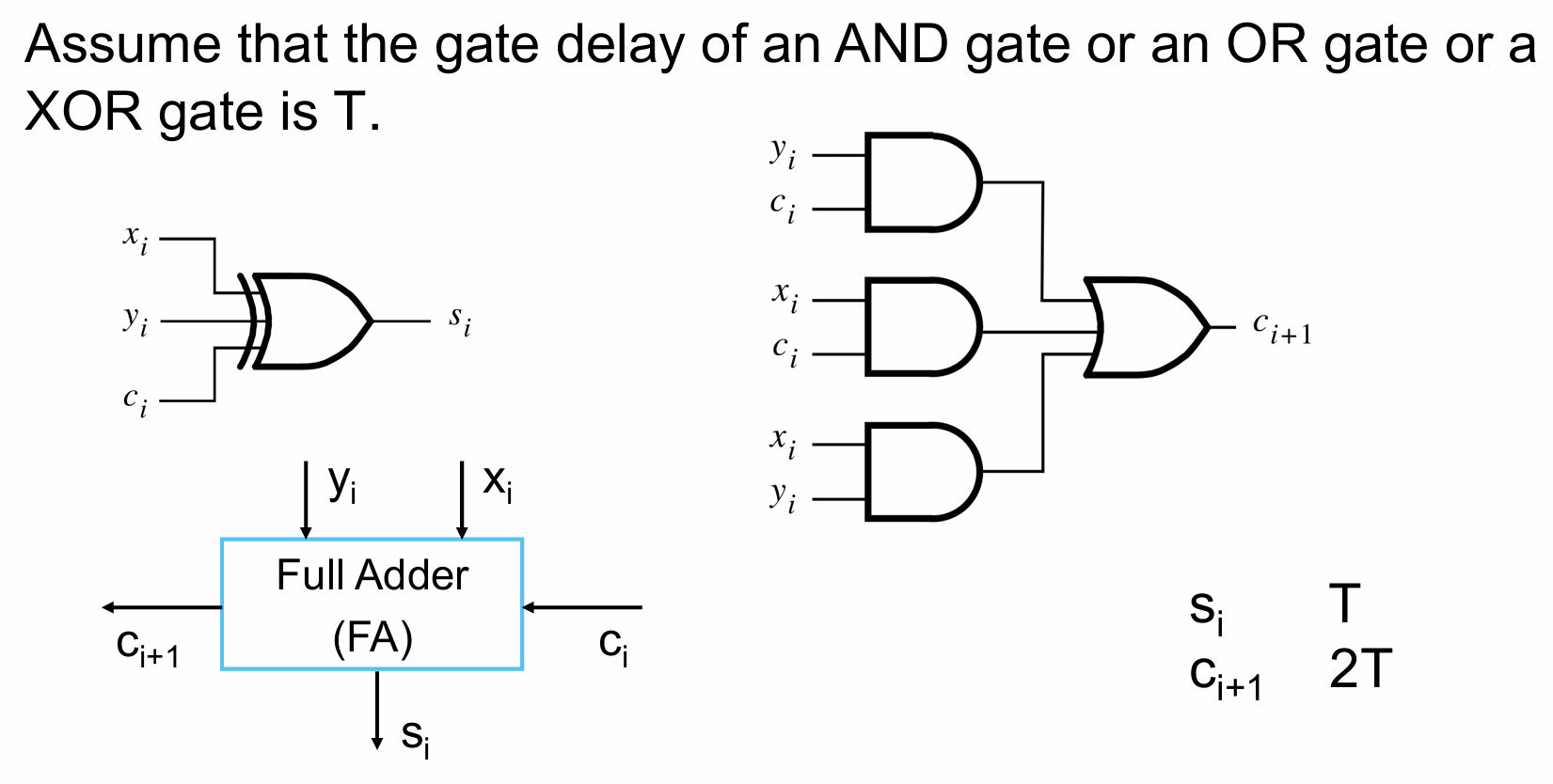
  • 全加器（FA, Full Adder）用于进行数的单位（1-bit）相加，如下图，$x_i$与$y_i$是相加的两个数的同位，$c_i$是上一位的进位数，这三个数作为输入到全加器内进行逻辑判断得到两个输出，$s_i$为留在本位的数，$c_{i+1}$作为下一位相加的进位数输入

FullAdder.png

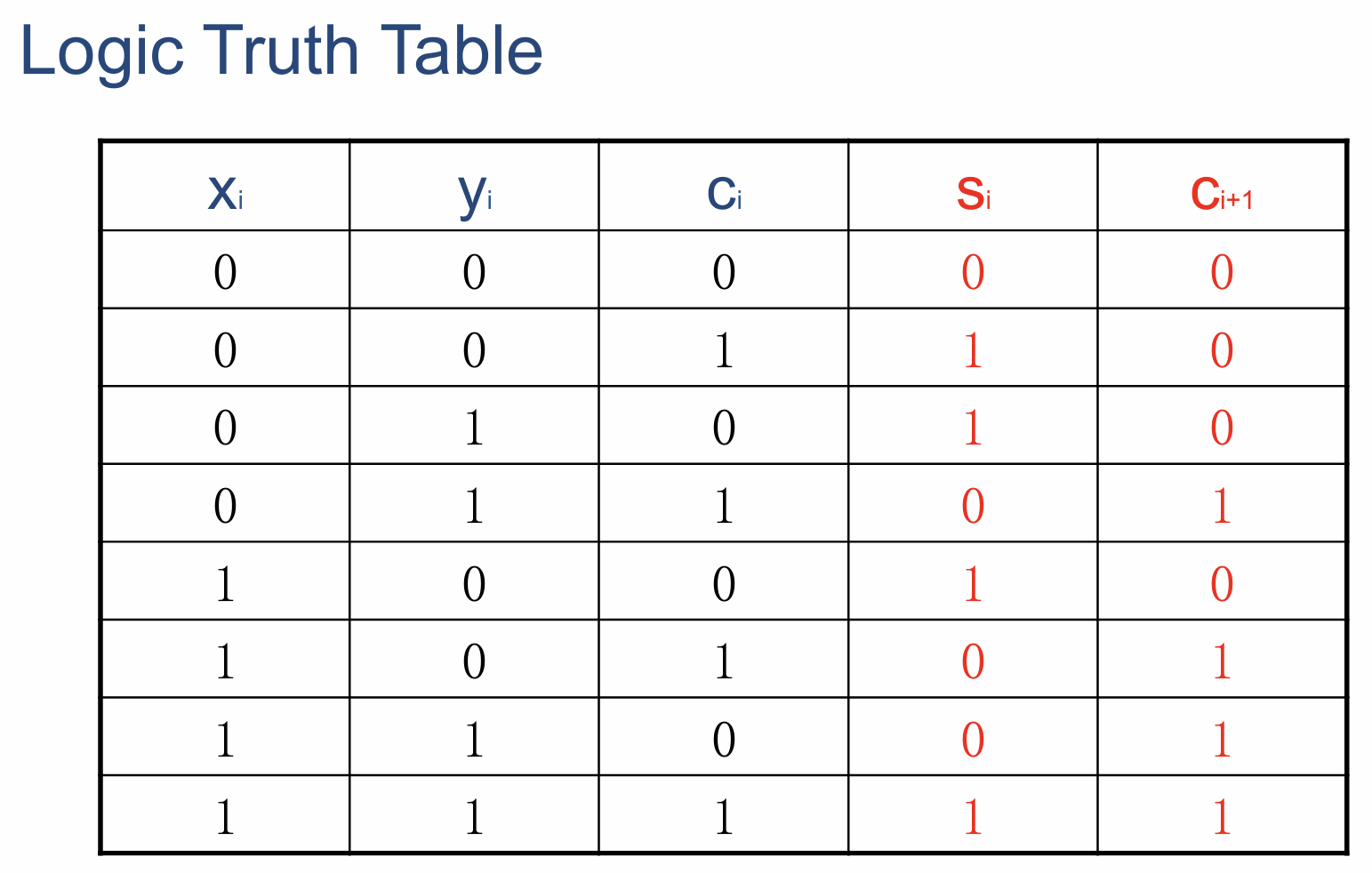
  • 全加器内进行的逻辑运算的结果以逻辑真值表的形式展示在下图

FullAdderTruthTable.png

  • 其中将$s_i$与$c_{i+1}$用$x_i$、$y_i$、$c_i$的逻辑关系的化简后表示如下
\[\begin{aligned} s_i &= (\neg{x_i}\wedge\neg{y_i}\wedge{c_i})\vee(\neg{x_i}\wedge{y_i}\wedge\neg{c_i})\vee({x_i}\wedge\neg{y_i}\wedge\neg{c_i})\vee({x_i}\wedge{y_i}\wedge{c_i}) \\ &= {x_i}\oplus{y_i}\oplus{c_i}\\ c_{i+1} &= ({x_i}\wedge{y_i})\vee({x_i}\wedge{c_i})\vee({y_i}\wedge{c_i}) \end{aligned}\]
  • 二者的逻辑门电路表示如下图，$s_i$只需一个三输入异或门即可

FA的s_i的逻辑.png

  • 得到$c_{i+1}$则需三个与门与一个能处理多输入的或门

FA的c_i的逻辑.png

2.3 行波进位加法器（n-bit）

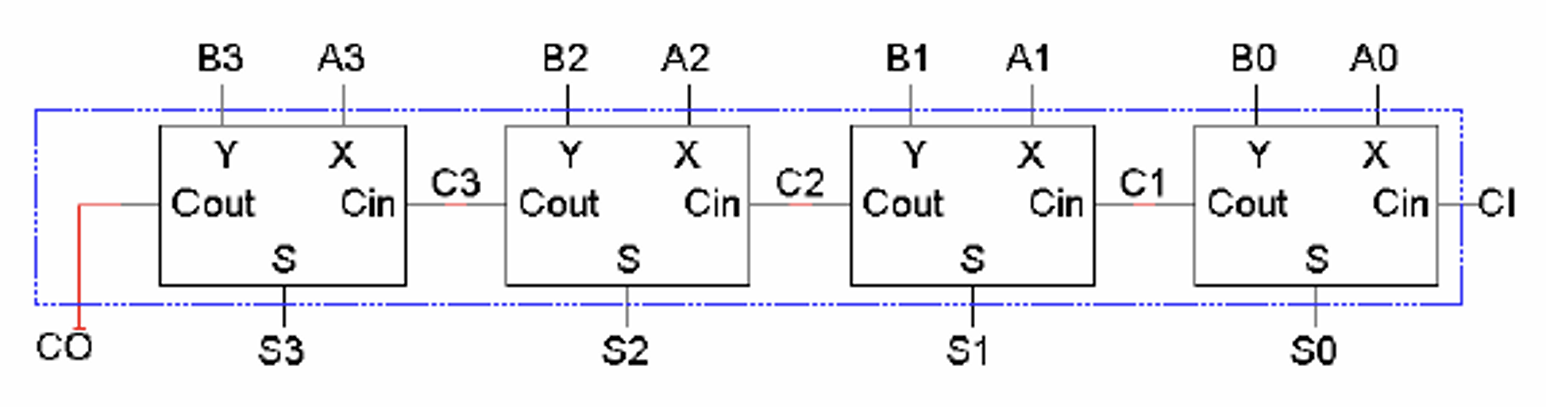
  • 四位行波进位加法器（4-bit Ripple-Carry Adder）实际上就是将四个全加器串联起来
  • 由于第一位是没有进位的，但是为了统一结构，第一位的全加器接收的进位数为$0$

4-bitAdder.png

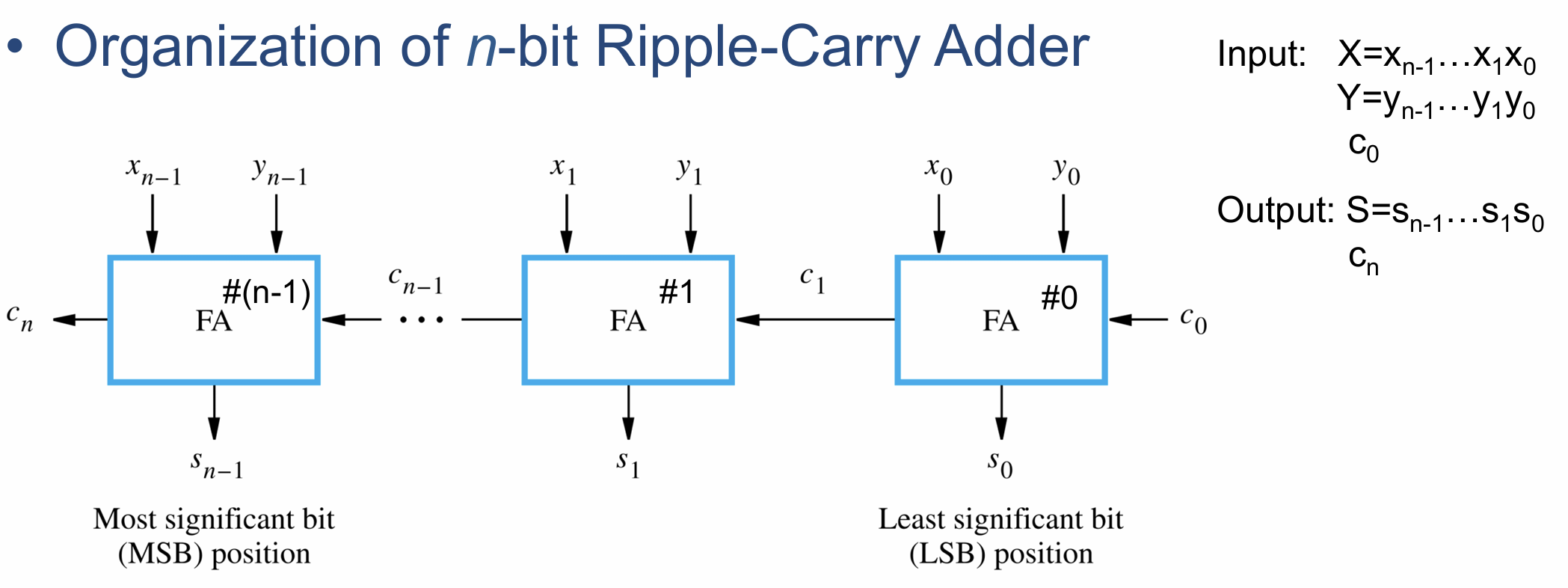
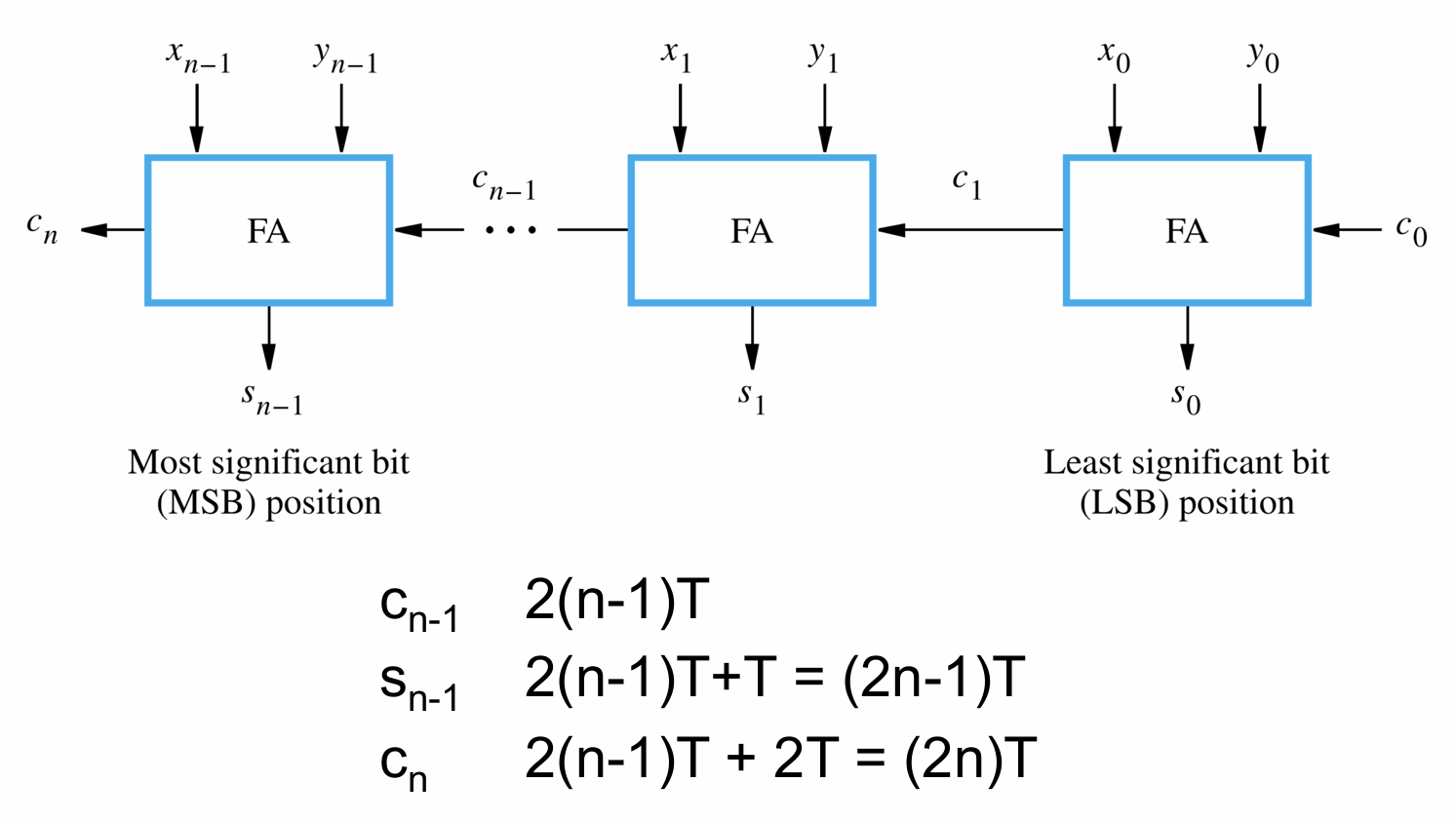
  • 继而可以使用全加器累积得到n位行波进位加法器

n-bitAdder.png

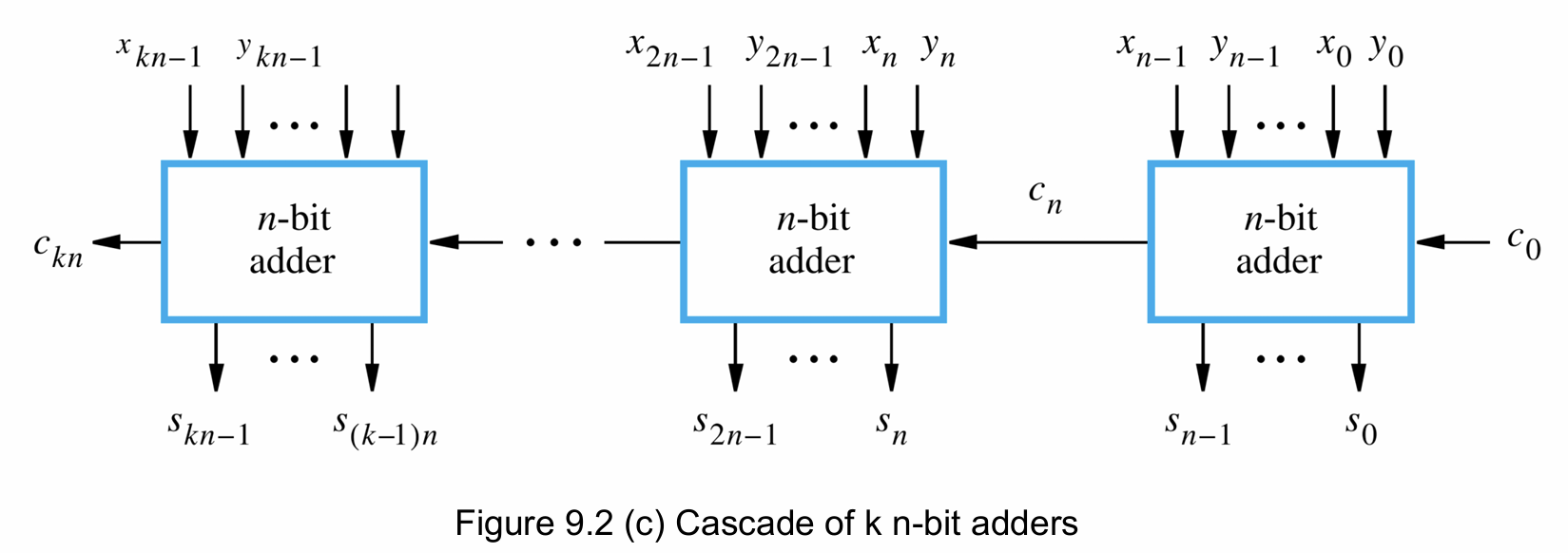
  • 继而使用k层n-bit加法器组成kn-bit加法器（Hierarchical Adder）

kn-bitAdder.png

2.4 溢出的判断

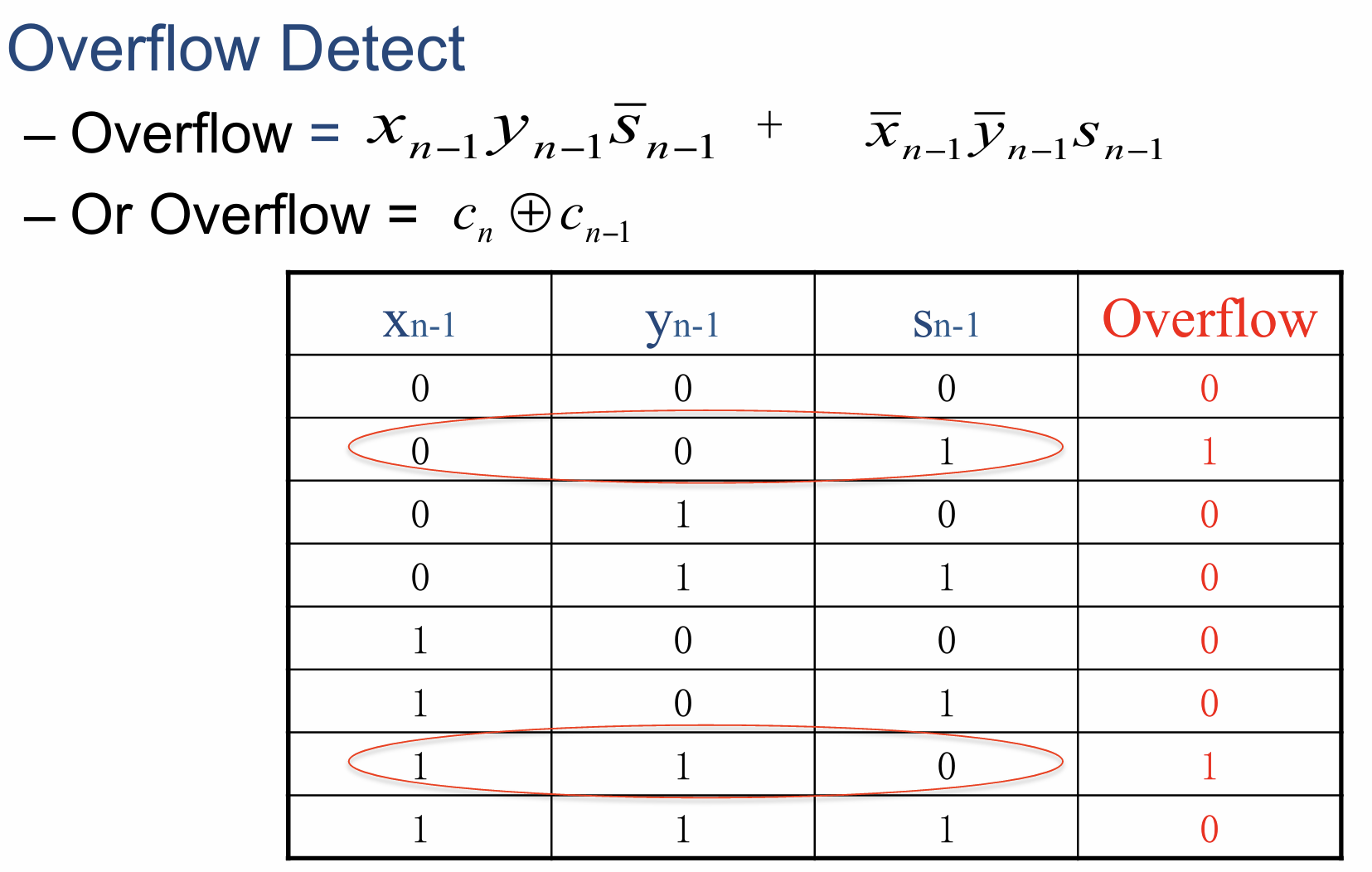
  • 由前面的知识可知，判断两个相同符号的数相加是否溢出只需看符号位$x_{n-1}$与$y_{n-1}$相同时（符号相异的两个合法数相加必定不会溢出）的输出结果符号位$s_{n-1}$与$x_{n-1}$的异同即可，相异则溢出
  • 判断逻辑及其真值表如下图所示，其中$\bar x$表示$\neg x$，加号表示$\vee$，相乘表示$\wedge$，注意到提供了两个判断逻辑，显然第二种仅需一个异或门是更优的

n-bitAdderOverflowDetect.png

2.5 门延迟与传播延迟

  • 每个逻辑门的输入和输出间有一段时间的延迟$T$，称为门延迟（Gate Delay），一般可以粗略将每个门的门延迟近似为相等，而一个复合的门系统的总传播延迟（Propagation Delay）取决于电路的结构
  • 下图示意的电路表示每次从输入到输出，得到$s_i$和进位$c_{i+1}$所耗费的总延迟，其中得到每个进位的总延迟就是$2T$，因为并行的那三个门是同时进行逻辑判断的，所以三个门处理逻辑所消耗的时间是$T$，和右侧串着的门共计$2T$延迟

复合门延迟示意.png

  • 在上面两个结论的基础上，我们可以得知n-bit行波进位加法器得到各输出的总传播延迟，得到$c_n$输出就需要$2nT$的时间，在此基础上得到$s_n$就需要$c_n+T = (2n+1)T$的延迟，得到$c_{n+1}$则需要$c_n+2T = (2n+2)T$的延迟，如下图所示

n-bitAdder传播延迟.png

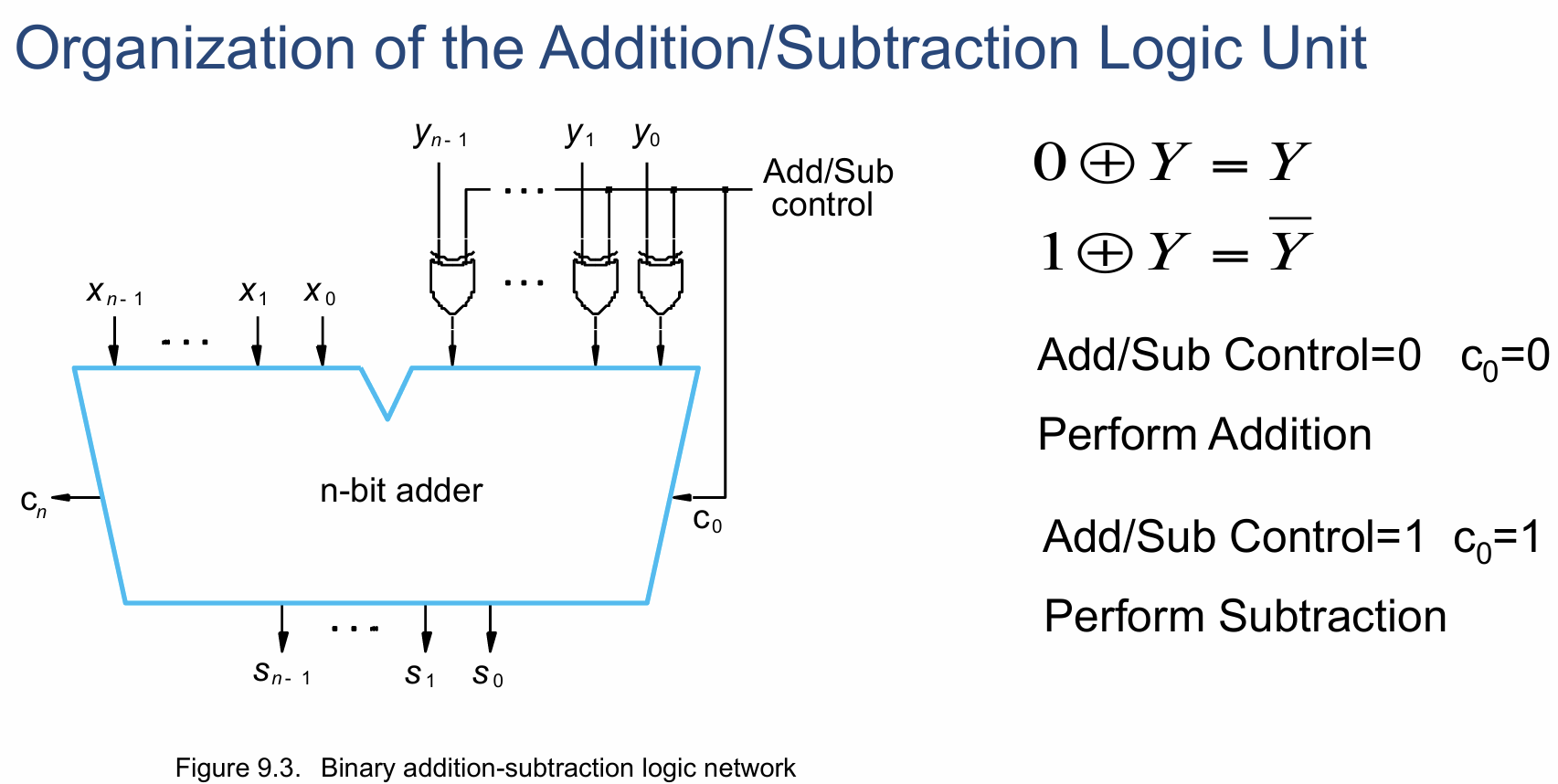
2.6 通用的加法/减法器

  • 下面这种设计能同时实现加法和减法（即比加法多了一个取补码的步骤）的计算

通用加法减法器.png

  • 此加减法器还可以加上一个异或门来检测溢出

三、快速加法器

3.1 超前进位加法器

3.1.1 逻辑原理

  • 行波进位加法器需要从低到高等待每一个全加器依次完成运算，产生的需要等待的门延迟较长，如$Delay(s_{n-1})=(2n-1)T$，以及$Delay(c_n)=2nT$
  • 在$x_i$与$y_i$均为$1$的情况下，两个二进制数的同一位（$x_i$与$y_i$）的相加运算一定产生进位$c_{+1} = 1$，与前一位的进位即$c_i$的值无关，但若是$x_i$与$y_i$仅有一个为$1$，那么就需要等待前一位的$c_i$的值来进行$c_{i+1}$的判断
  • 超前进位加法器（CLA, Carry-Lookahead Addition）就是依据上述原理，将不依赖于$c_{i-1}$的那部分判断在所有位上先并行运算，然后再依据$c_{i-1}$的值进行最终的计算
\[c_{i+1} = (x_i \wedge y_i)\vee(c_i \wedge (x_i \oplus y_i))\]

3.1.2 电路结构

超前进位加法器通过更加复杂的硬件结构来换取时间的优化（以空间换时间）

  • 从$c_{i+1} = (x_i \wedge y_i)\vee(c_i \wedge (x_i \oplus y_i))$中提取$G$（Generate Function）和$P$（Propagate Function）
    • 其中信号$P_i = x_i \oplus y_i$换为$P_i = x_i \vee y_i$也没错，但是这样就需要多使用一个或门
    • 这两个信号可以在刚输入$x_i$与$y_i$的时候就并行运算而无需等待$c_i$
\[\begin{aligned} &G_i = x_i \wedge y_i \\ &P_i = x_i \oplus y_i \end{aligned}\]
  • 然后式子就可以简化成如下形式
\[c_{i+1}=G_i \vee (P_i \wedge c_i)\]
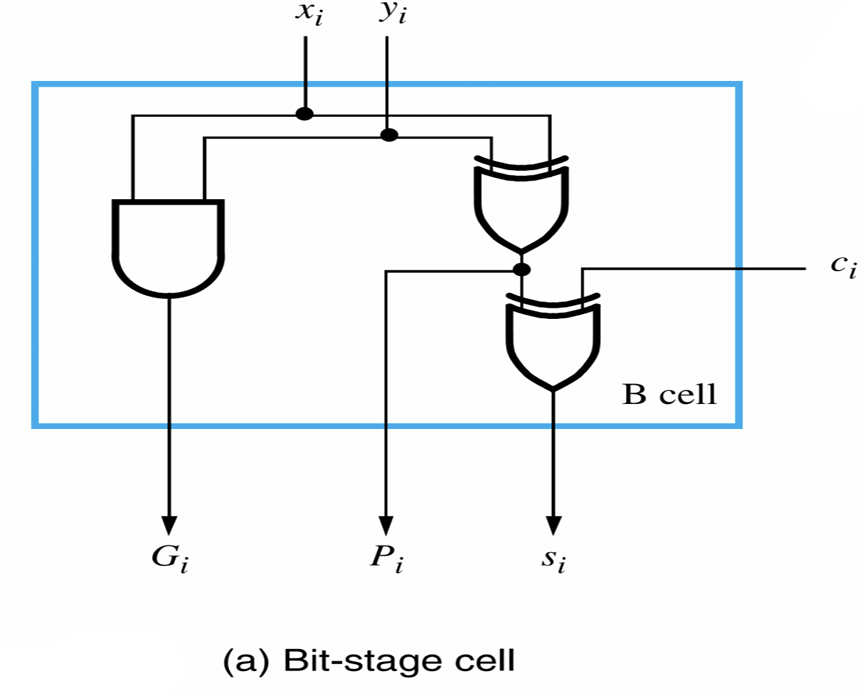
  • 超前进位加法器的基本结构B-Cell如下图所示
    • 该结构把计算$s_i = x_i \oplus y_i \oplus c_i$使用的异或门拆分为两个，使得$P_i = x_i \oplus y_i$的结果能被记录
    • 用于计算$G_i$的与门可以与第一个或第二个异或门并行运算，以提升时间效率

B-Cell示意.png

  • 经历了上面的单元后，然后再对$G_i$和$P_i$结合$c_i$进行判断，输出$c_{i+1}$

超前加法器全貌.png

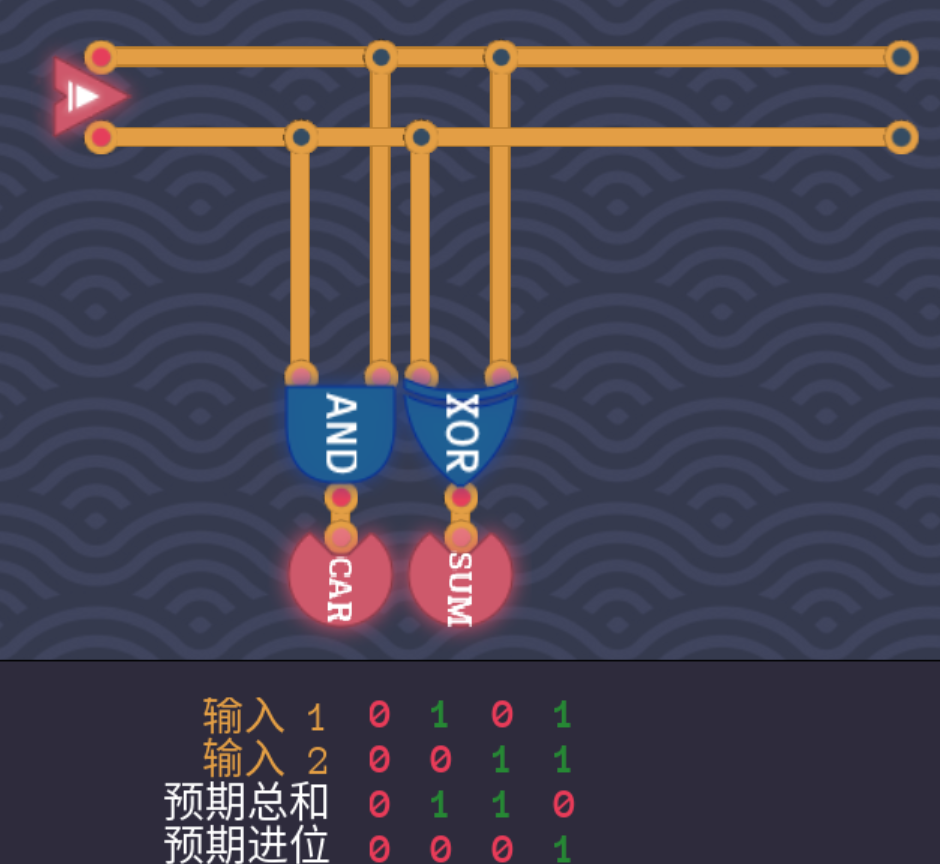
  • 在游戏《图灵完备》中实现的的半加器如下

图灵完备半加器.png

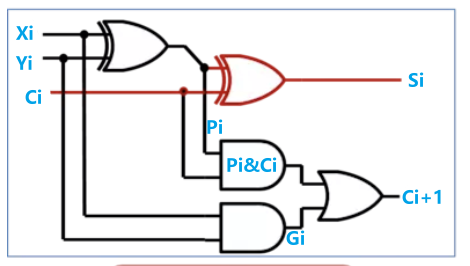
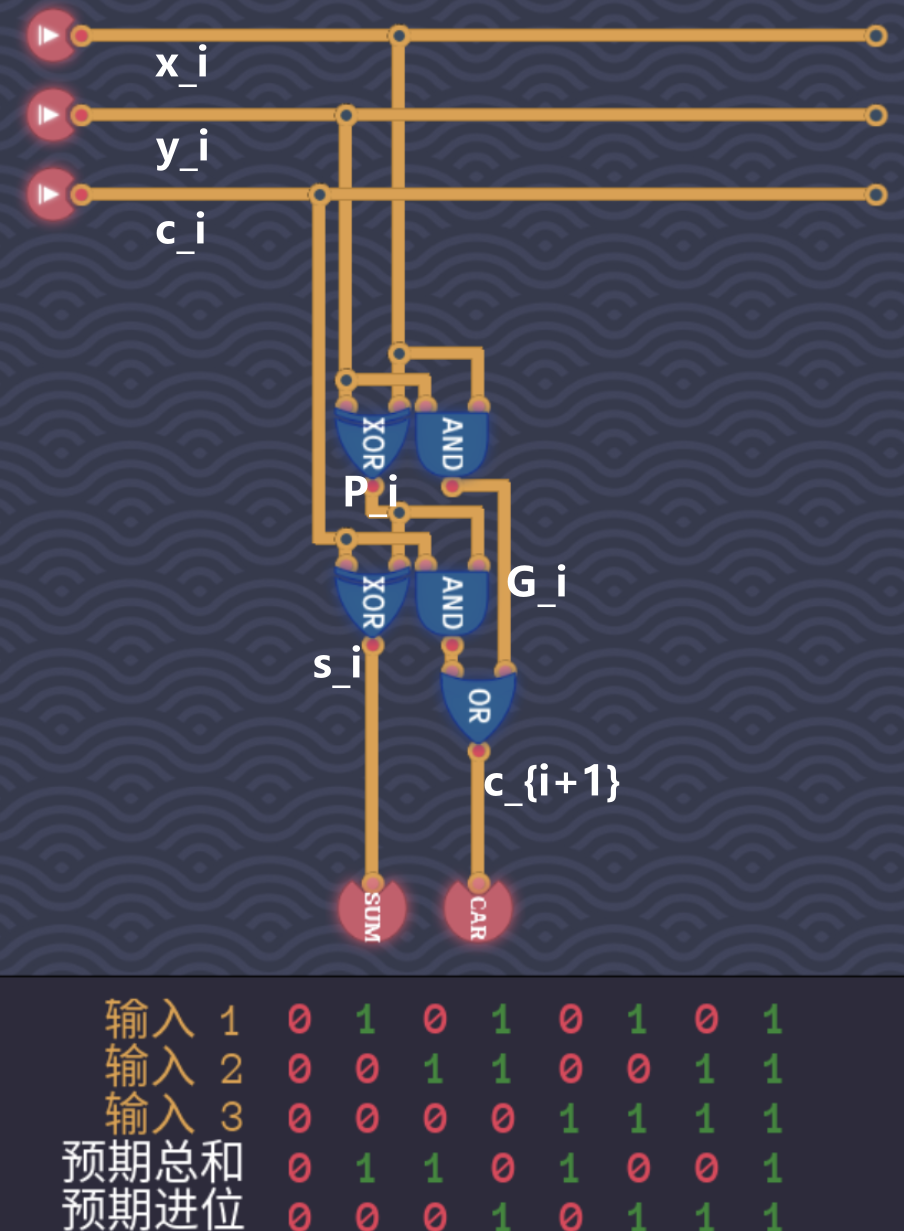
  • 用两个半加器以及一个或门可以组成如下图的全加器即B-Cell如下，由两个半加器外加与门实现

图灵完备全加器.png

3.1.3 传播延迟

  • 假设所有门的门延迟都是$T$，那么可从电路结构上看出，对于单个CLA，从$x_i$、$y_i$和$c_i$被输入后
    • 到得到输出结果$c_{i+1}$，耗费的传播延迟是固定的$3T$
    • 到得到输出结果$s_{i}$，耗费的传播延迟是固定的$2T$
  • 如果考虑多个CLA的结构的话
    • 从输入$c_i$开始到得到得到$s_{i+1}$（下一位的结果位）所耗费的传播延迟是$3T+T=4T$，其中$3T$是从$c_i$到$c_{i+1}$的延迟，$T$是从$c_{i+1}$输入，到得出$s_{i+1}$的延迟（下一位的$x_{i+1}$和$y_{i+1}$的相关计算已并行完成就绪了，所以无需等待$P_{i+1}$和$G_{i+1}$的计算）

3.2 扇入与扇出

  • 扇入（Fan-In）指的是一个逻辑门接收的输入的个数
  • 扇出（Fan-Out）指的是一个逻辑门产生的输出的个数
  • 电路中不允许有过大的扇入或者扇出，这样会影响运算效率

3.3 组合CLA

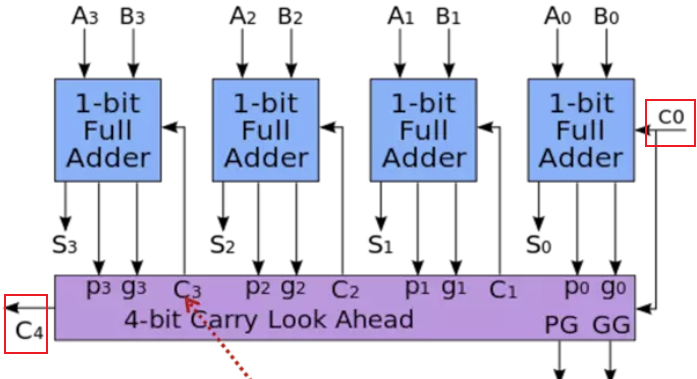
3.3.1 四位组合CLA

  • 四个CLA并联在一起，可以实现并行计算，如下图所示，从$c_0$得到$c_4$的总延迟是$3T$

4-bitCLA示意..png

3.3.2 八位组合CLA

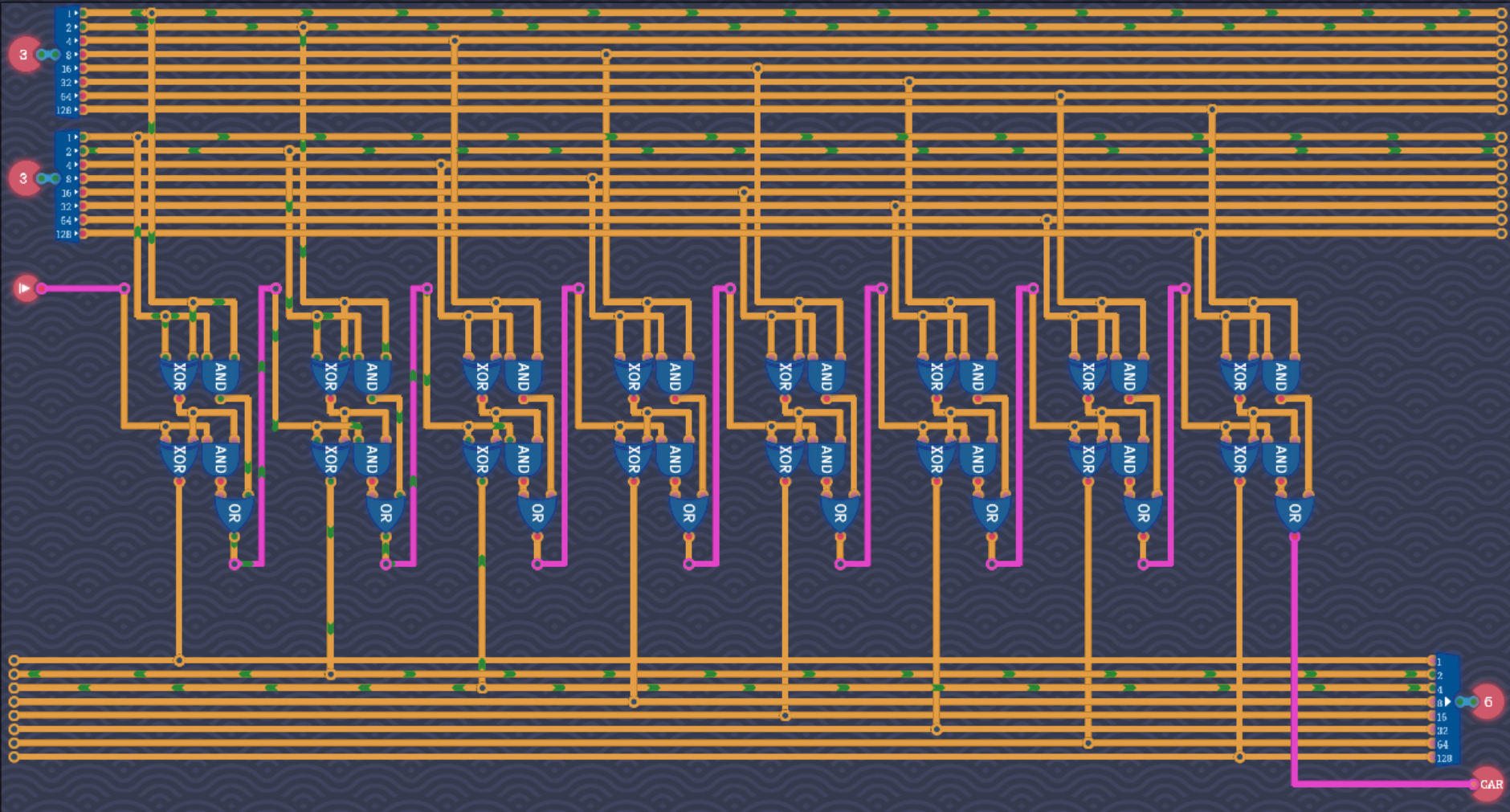
  • 在游戏《图灵完备》中实现的8-bit超前进位加法器如下，可以看到此加法器内部有8个全加器，左上角的输入端有三个信号，即两个8bit的二进制数以及一个进位信号（紫色的线传输的是进位信号），最终输出一个8bit二进制数以及一个进位信号到右下角

图灵完备8bit超前进位加法器.png

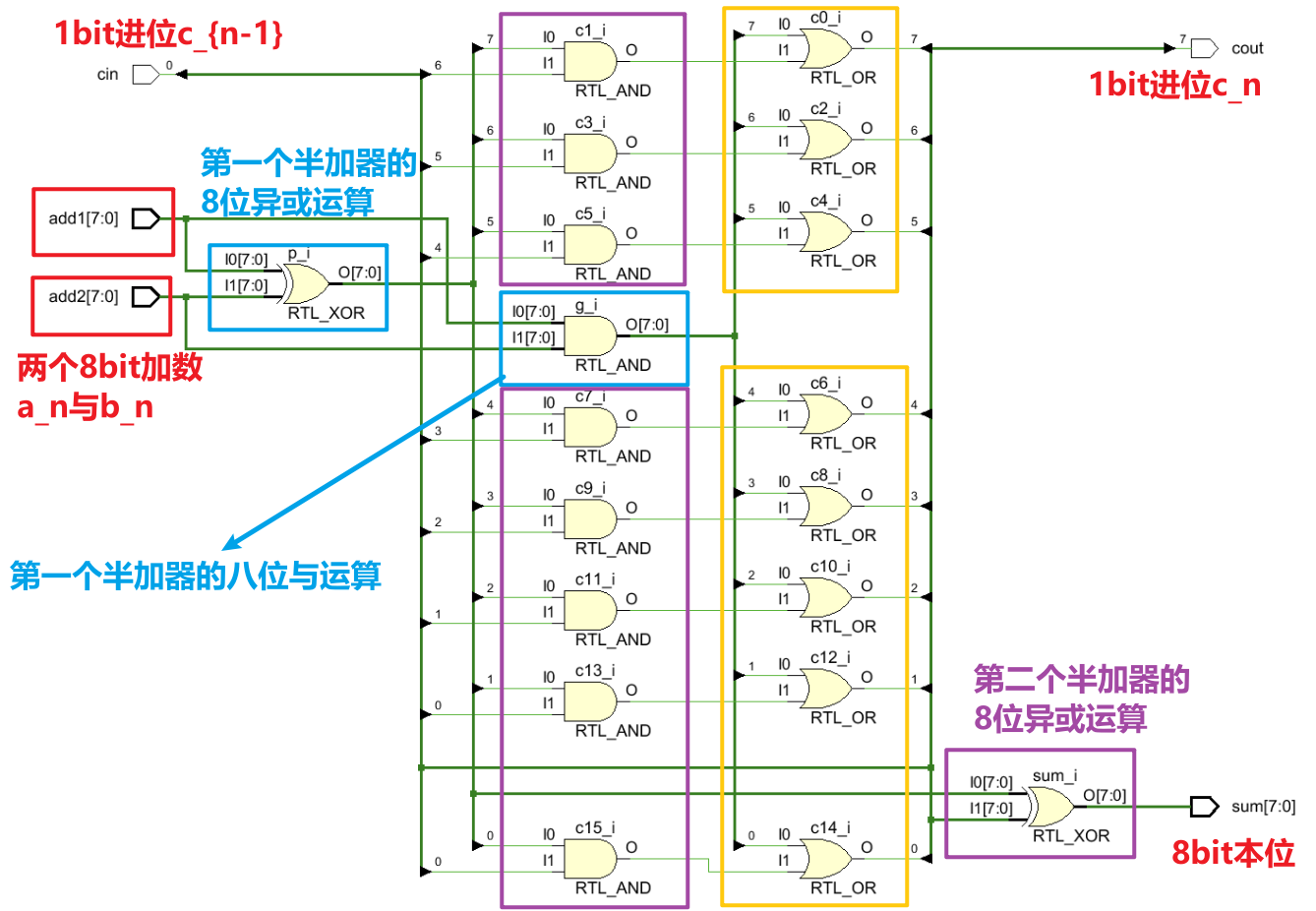
  • 仿真电路中长这样，注意区分其中的门运算器有8bit的（已标注）和1bit的，原理同上

八位超前进位加法器电路图.png

3.3.3 n位组合CLA

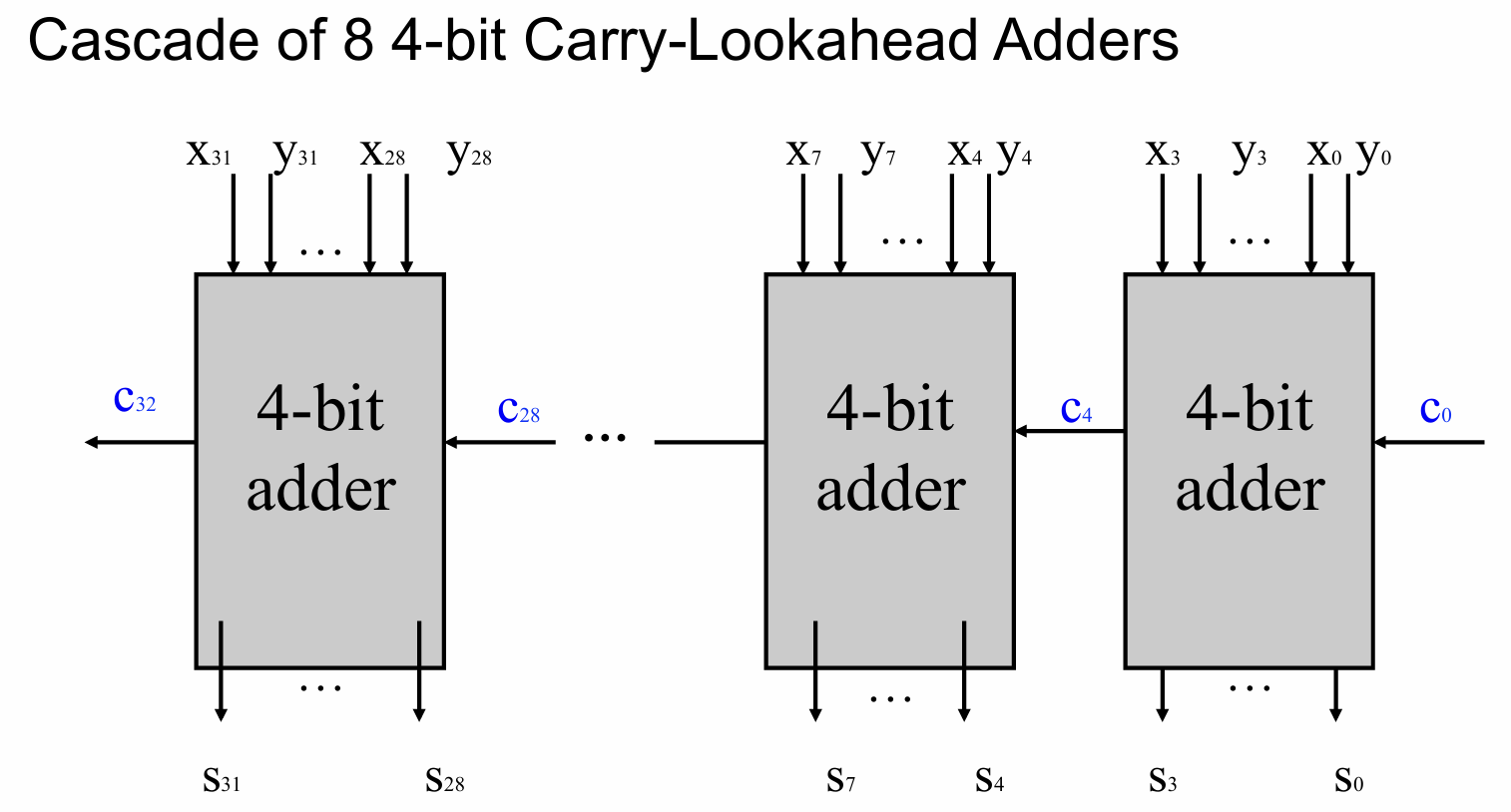
  • 过长的CLA组合在一起的话，会导致电路结构非常复杂，所以我们一般采取串联多个组合的CLA组成一个较大的加法器，比如8个4-bit的CLA组成一个32-bit的
  • 代价就是从输入到输出的门延迟是无法被完全并行优化掉，因为是串联所以后面的4-bitCLA需要等到$c_{4n}$的输入，但是信号$P$和$G$却无需等待，所以这部分延迟是可以被并行掉的，故而被累加到总的传播延迟的延迟只有$3T-T=2T$之多

多个4-bitCLA的级联.png

  • 例题：对于8个4-bit的CLA组成一个32-bit的加法器，求得到其某个$c$或$s$输出所耗费的延迟，如下图所示，$c_4$由于是并行的CLA运算，所以传播延迟$3T$；$c_8$是第二个4-bitCLA的输出，由于其在第一个4-bitCLA运算的时候就得出了各位的$P$和$G$，所以其只需要在总传播延迟上加上$2T$

8x4-bitCLA延迟计算.png

四、整数乘法运算

4.1 二进制乘法

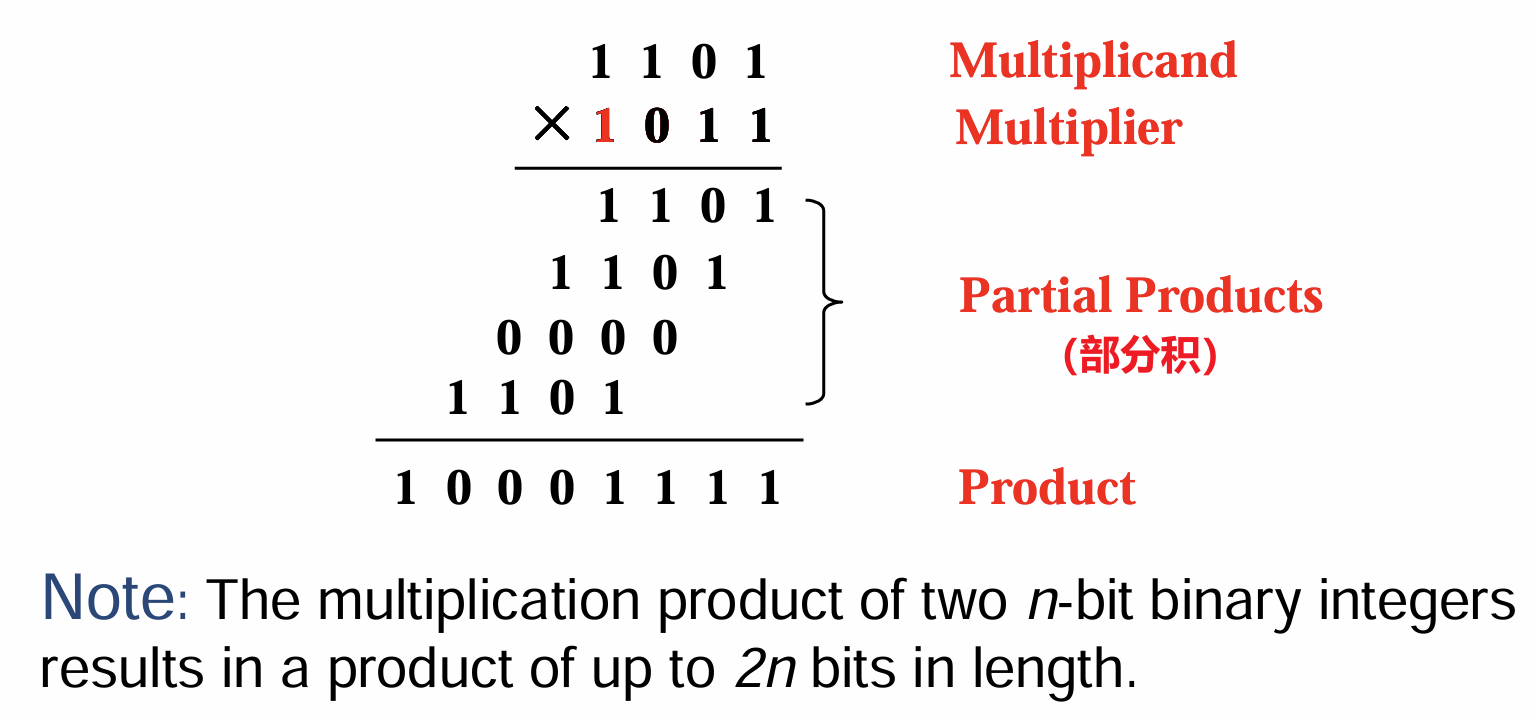
  • 二进制乘法与十进制的竖式同理

二进制乘法竖式示意.png

  • 抽象为字母$M$、$Q$、$P$表示输入和输出

二进制乘法的抽象竖式示意.png

4.2 无符号数的阵列乘法

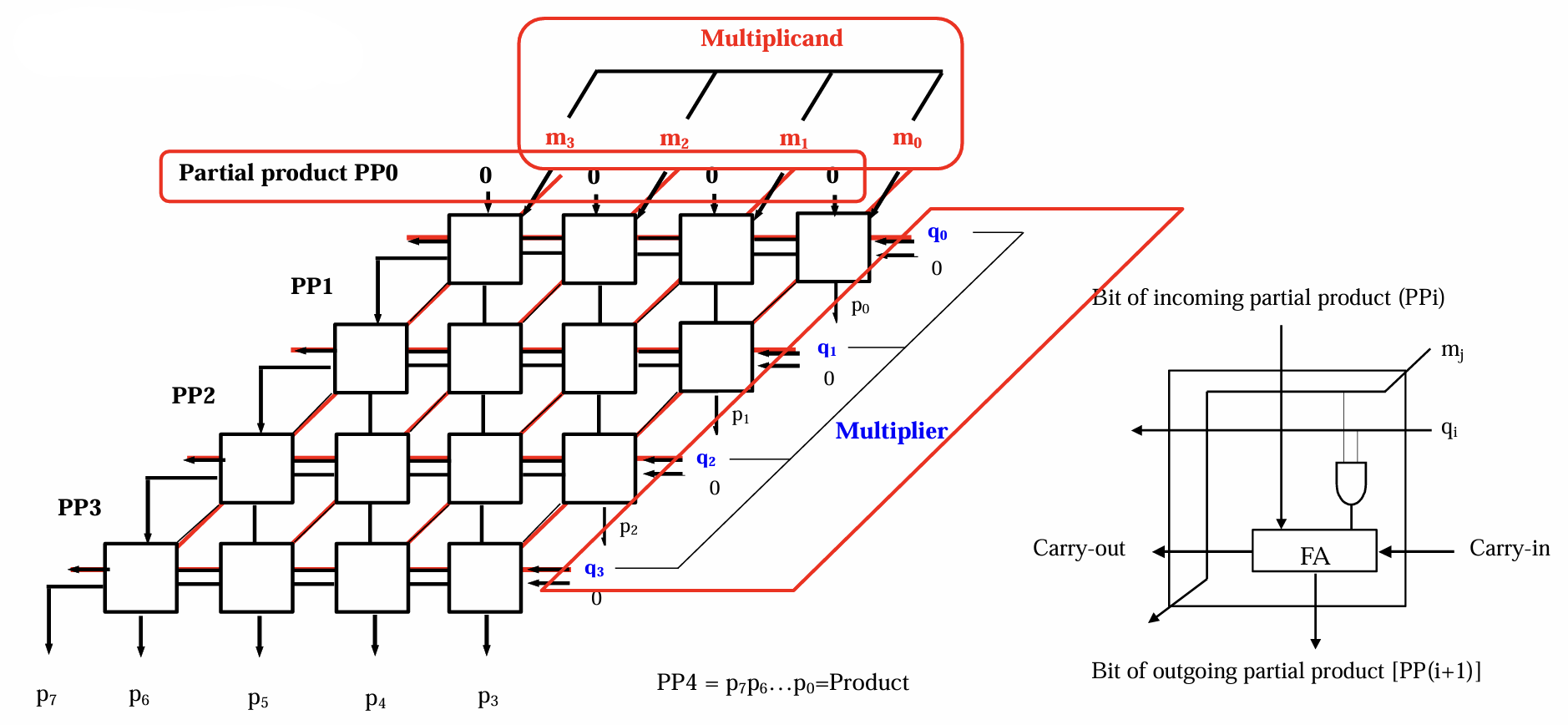
  • 阵列乘法使用竖式乘法的逻辑进行运算，其硬件实现较为复杂
  • 以无符号的两个4-bit数的乘法示意，其实就是从第一行部分积开始与第二行做加法，然后将结果向下以此类推

硬件阵列乘法示意.png

  • 上图的每个小方格即表示一个$PPi$，注意到每个$PPi$拥有一个FA结构（用于位运算）和一个与门
  • 注意第一行由于只需要与$0$做加法，所以第一行的$PPi$不需要FA，所以一个nxn的乘法，所需要的FA模块个数是$n(n-1)$个，而与门的个数是$n^2$个

4.3 无符号数的顺序乘法

4.3.1 硬件原理

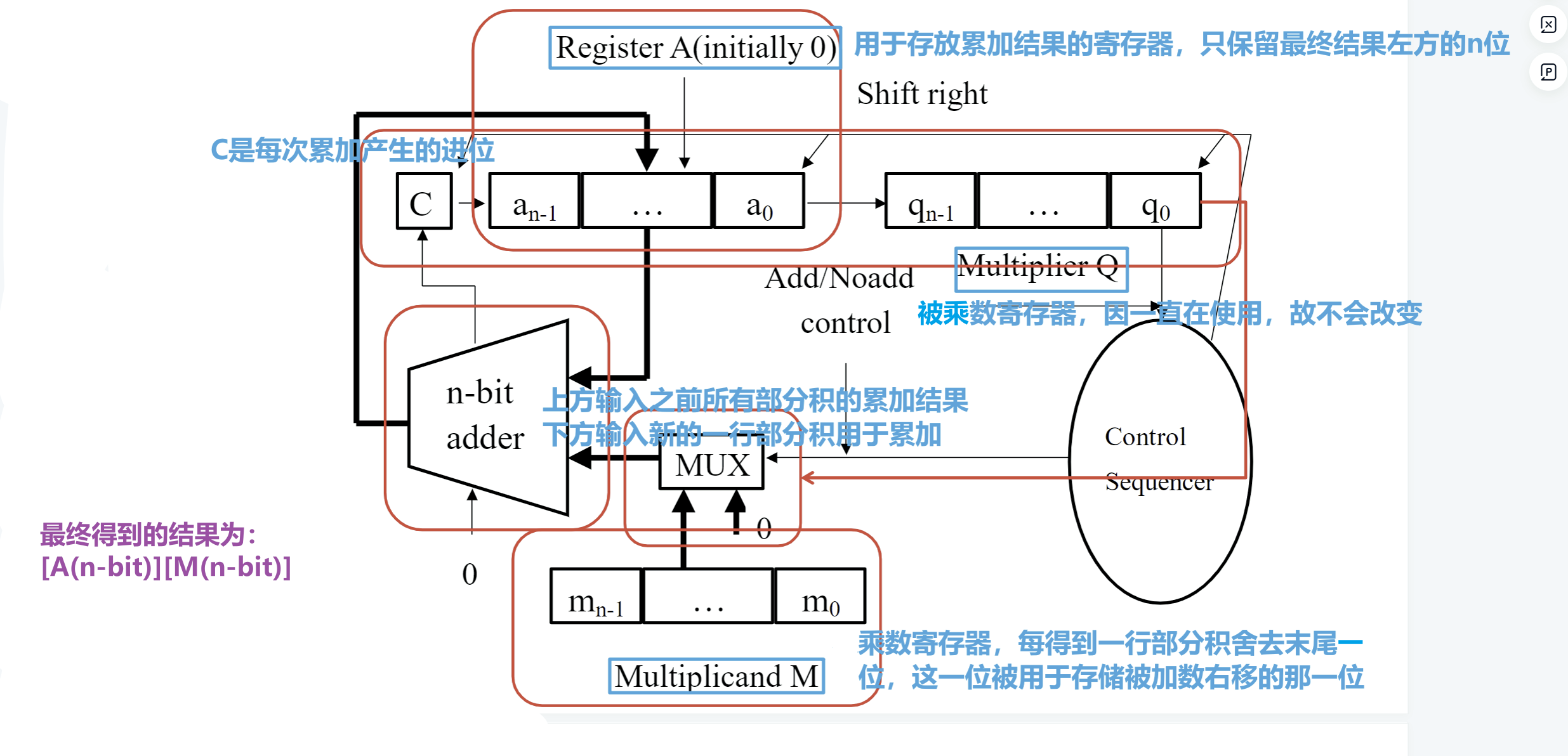
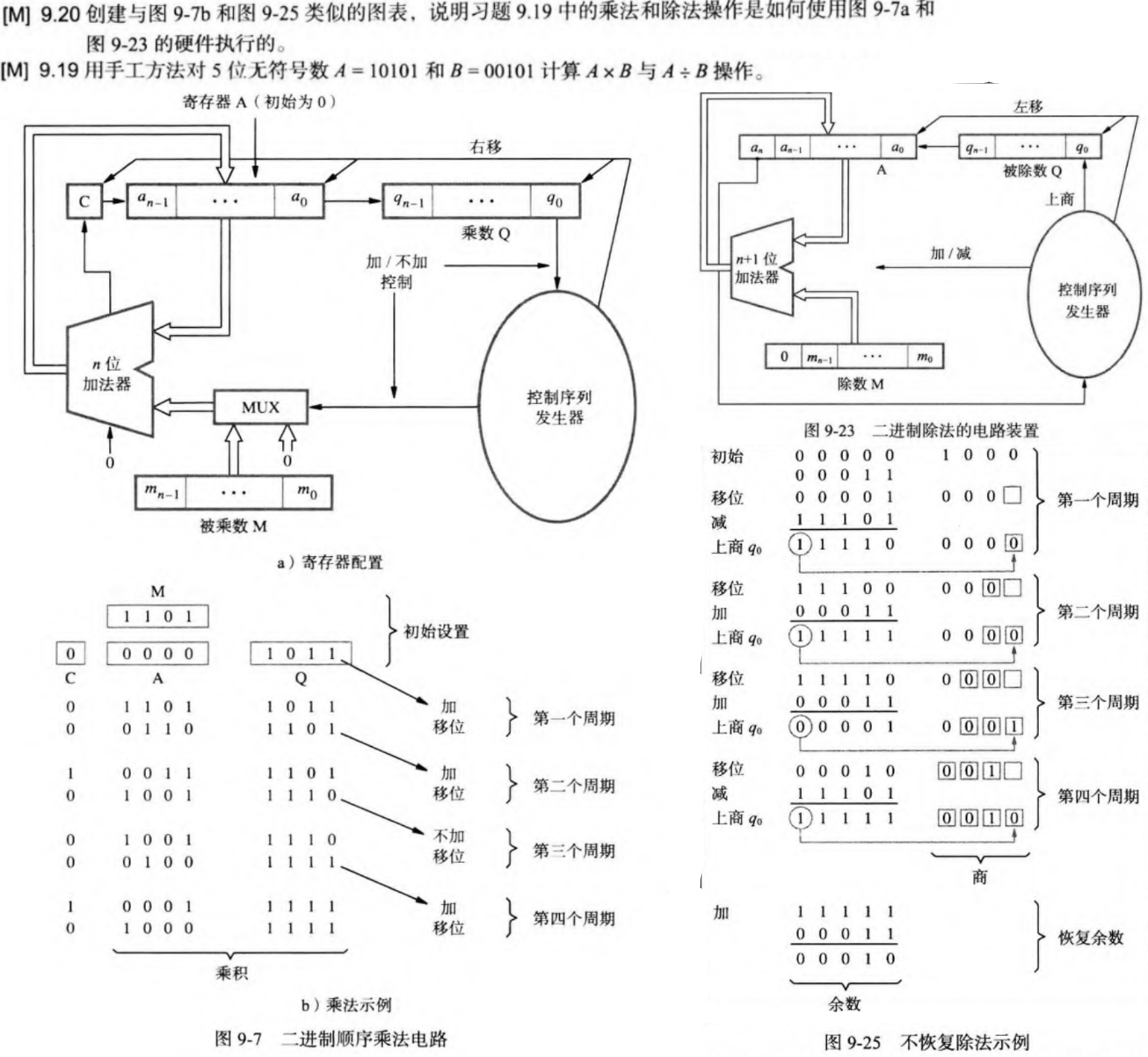
  • 乘法还可以通过线性的电路来实现，无符号的两n-bit数的乘法只需要一个n-bit的加法器、三个n-bit寄存器、一个1-bit寄存器存储每次累加的进位
  • 其硬件电路结构示意及其详解如下图所示（关于英文单词Multiplier和Multiplicant到底谁是乘数谁是被乘数貌似仍有争论…？）

顺序乘法器的硬件原理.png

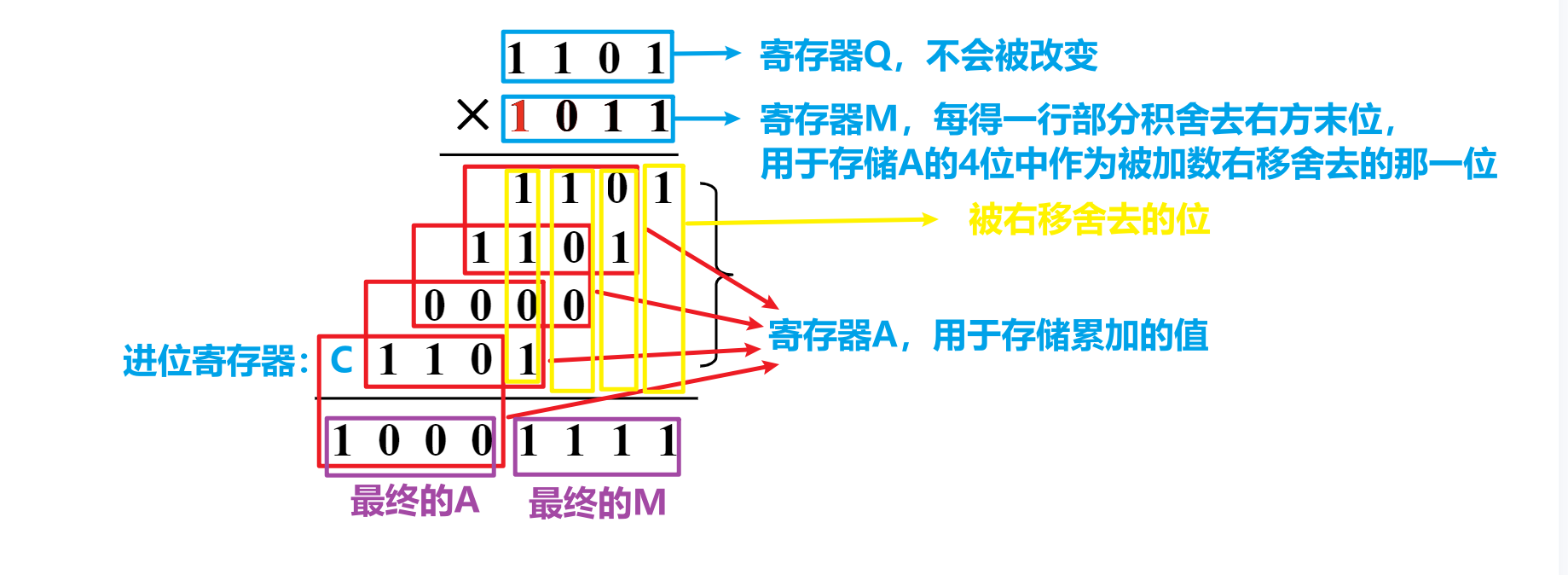
  • 结合上述结构，我们参考下图，以顺序乘法计算4x4的乘法；下图的每个红框内的两行相加之和（作为新的一行）存储在A寄存器中，相加产生的进位存储在C寄存器中，（C与舍去末位的A组成一行4bit的数，作为下一个红框的第一行参与计算，一定要注意这一点，因为下图没办法表示这个过程，所以第2、3、4个红框框住的第一行并不是实际参与其运算的，实际参与的应当是上一次红框运算产生的C与减去一位的A），第一个红框左上角是0，剩下的三个红框的左上角都是C，即上一个红框内的相加运算产生的进位

顺序乘法的4x4示例.png

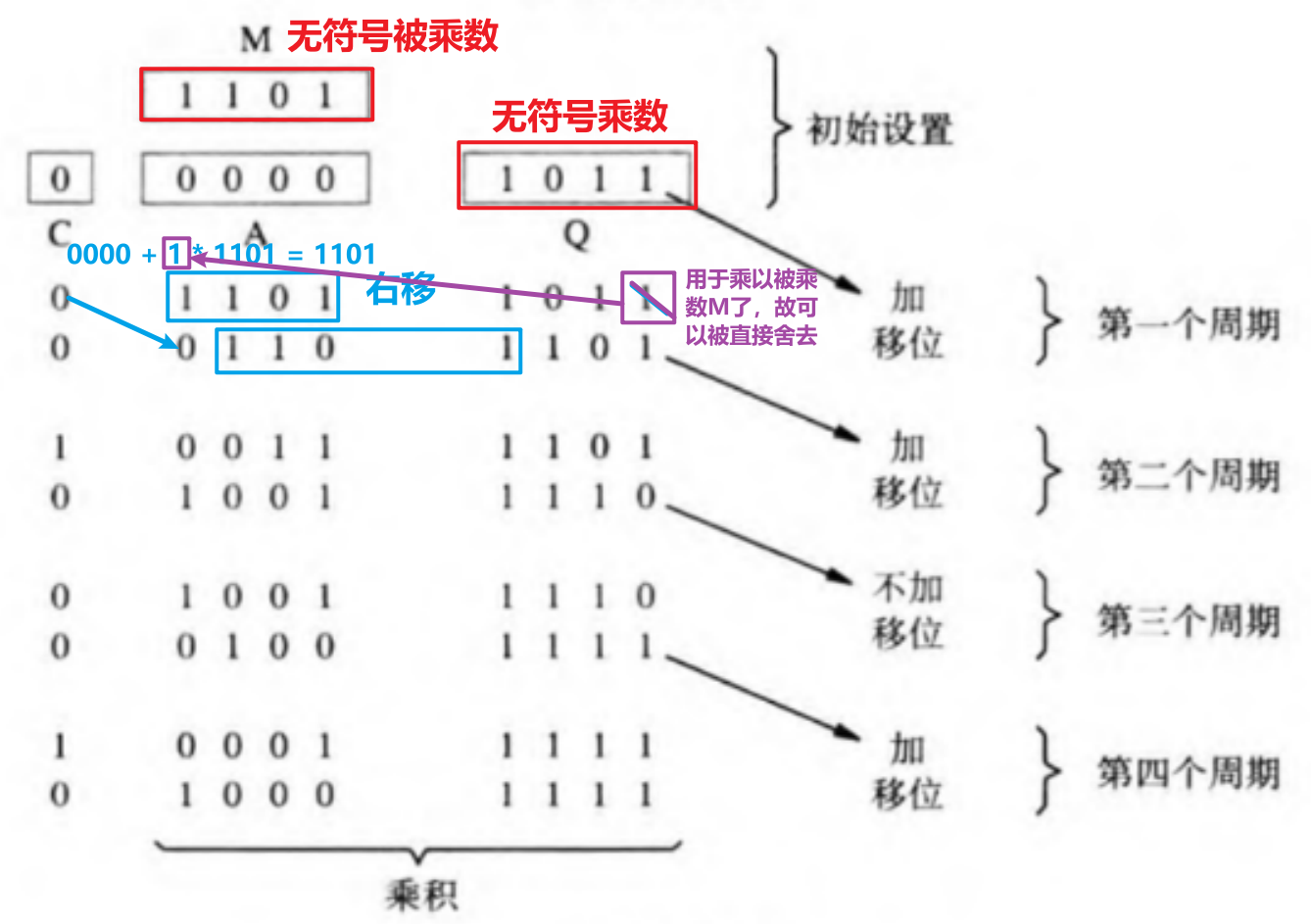
4.3.2 算法图示

  • 具体流程如下所示，四位数相乘的话，就类比重复第一个周期的步骤四次，总共进行四个周期即可得到最终的乘积结果

无符号乘法的示意图.png

4.4 有符号乘法（Booth算法）

4.4.1 产生背景

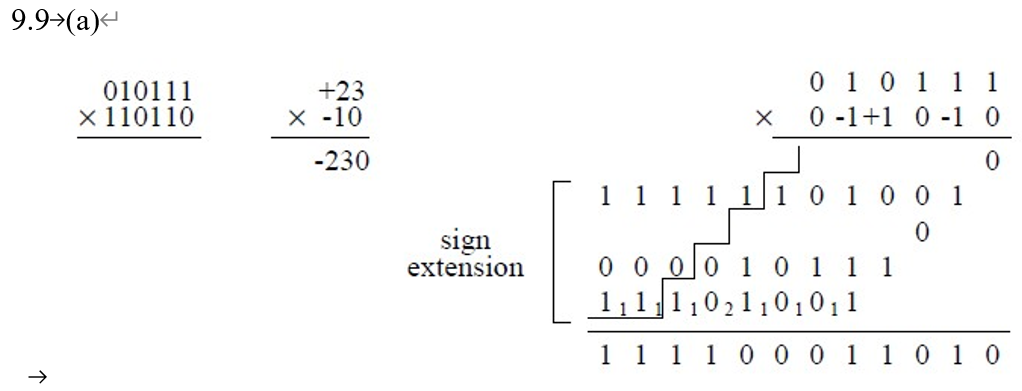
  • 对于有符号数的乘法，可以将有符号数（比无符号数多一位符号位）转化为无符号数后相乘，然后单独计算符号位，再将结果的无符号数结合符号位计算结果转化为有符号数，这样的硬件实现太过复杂，并且运行效率太低
  • 下图展示了为何直接进行有符号数补码的运算行不通（请注意下面得出的答案是错误的）

示意为何直接进行有符号数补码的运算行不通.png

4.4.2 算法原理

  • 布斯算法能够直接计算两个有符号数（补码）的乘法，我们需要将乘数进行一个转换，依照下表
  • 其中被转换数的最低位$x$（最右侧的位）可能是$0$或$1$，将其视作右侧有一个$0$的对象即$x0$，从而可以套用下表的转换，例如$abc1$转换为$a’b’c’(-1)$，$abc0$转换为$a’b’c’(0)$

布斯算法补码乘数转化表.png

  • 转换完之后就可以直接进行乘法计算了，注意每行部分积需要进行补位（使用符号位数补全）

布斯算法补码乘数转化后运算实例.png

4.4.3 硬件实现

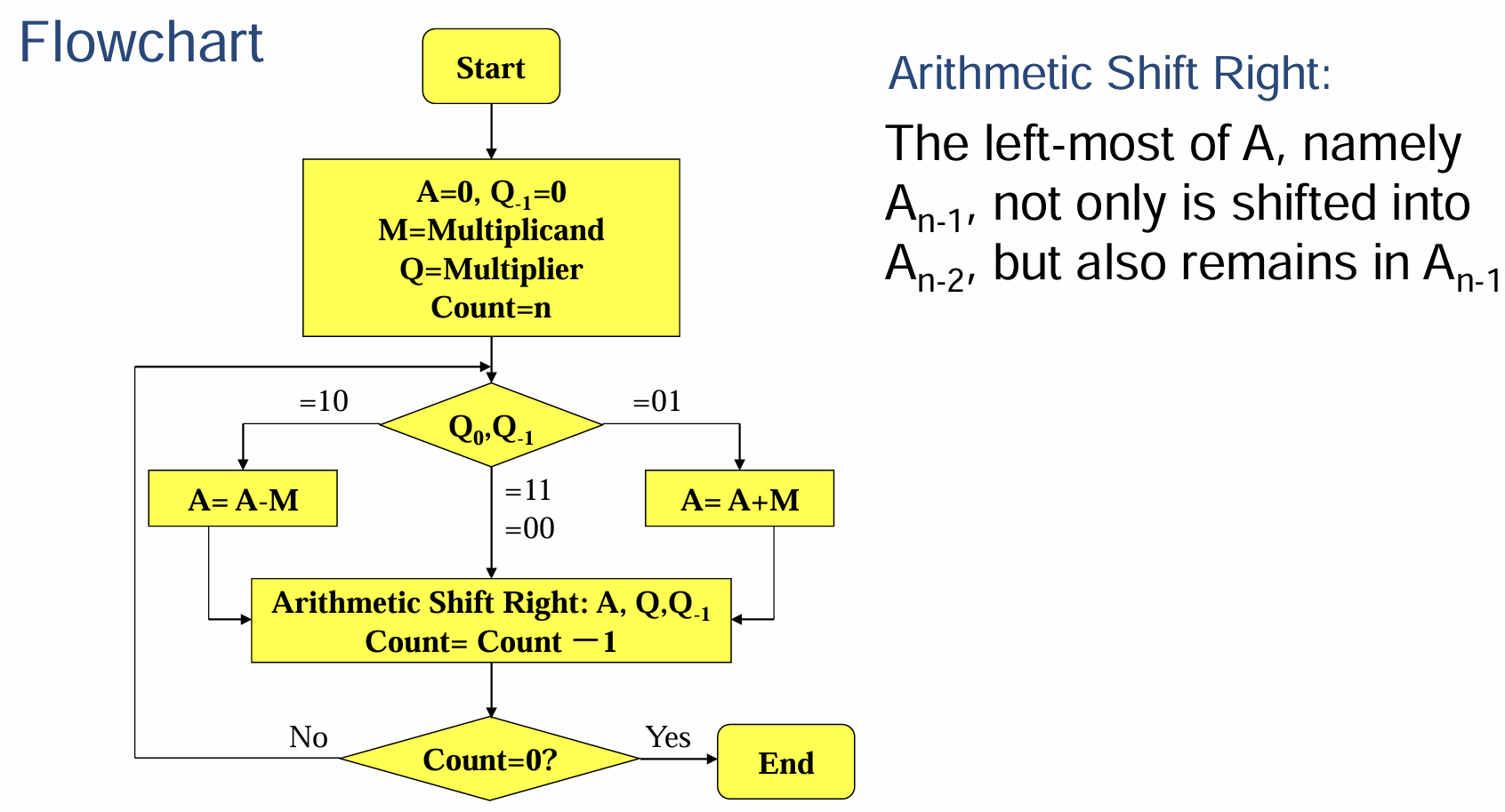
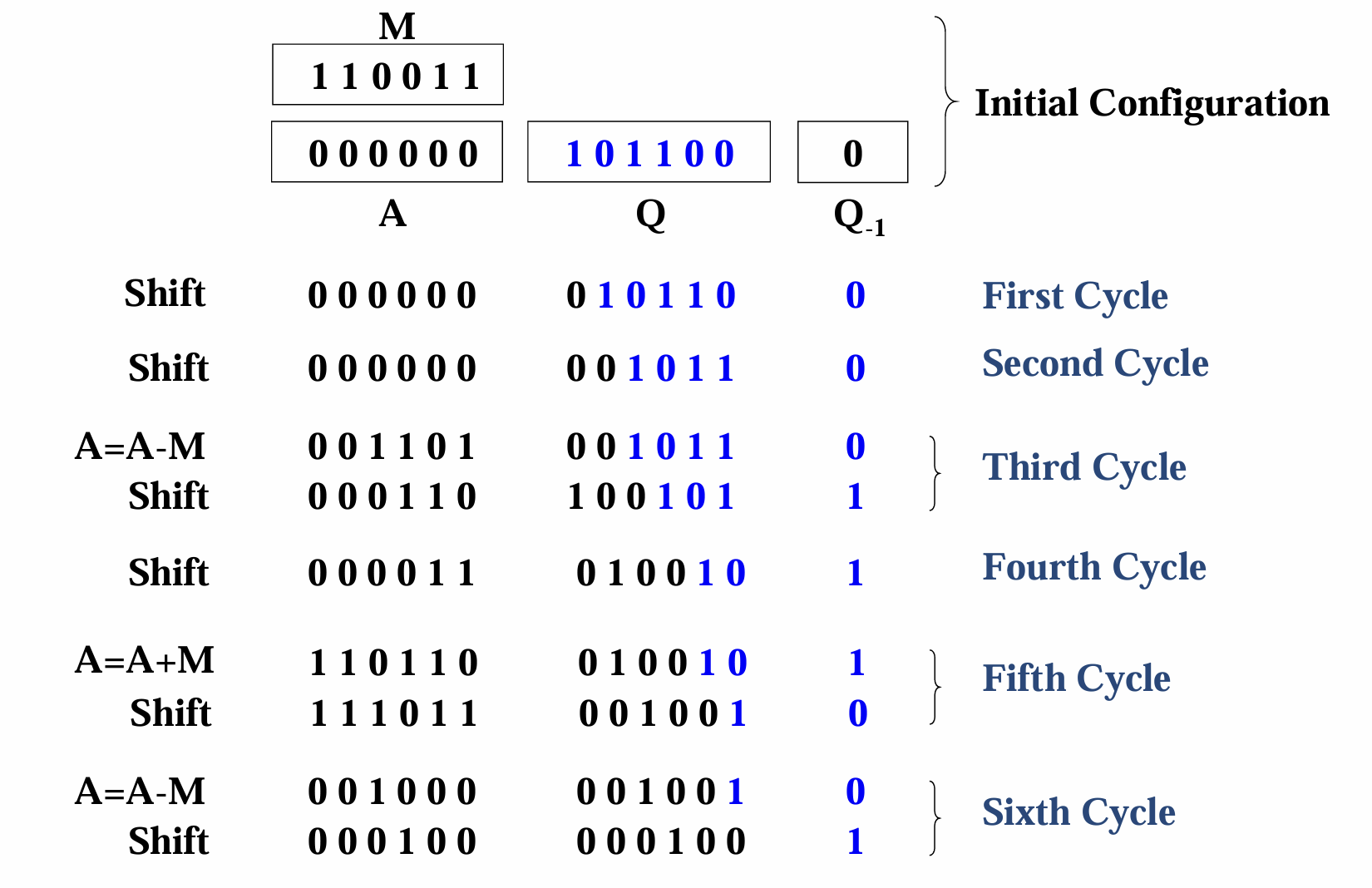
  • 硬件原理的流程图与流程解释如下
    • $A$是存储结果的寄存器
    • $M$是被乘数寄存器
    • $Q$是乘数寄存器，$Q_0$指的是$Q$最右侧的末位数（不知道为什么下面例子中的两个相乘的数跟“无符号数的顺序乘法”的符号表示是反过来的，可能PPT搞错了）
    • $Q_{-1}$是1-bit寄存器，Count初始化为两个数的位数，每次进行$Shift$操作后递减，直到为$0$就结束运算（因为$n\cdot n$的乘法运算得到的部分积就是$n$行的，所以进行$n$次运算即可）
  • 其中$=10$、$=01$、$=11$、$=00$指的是对$Q_0$和$Q_{-1}$这两个bit组成的数进行判断，然后决定下一步要做什么操作
  • $Shift$指的是算数右移，即把$A$与$Q$的末位取出，其余位整体向右移，$Q$的末位数转移到$Q_{-1}$上；$A$的符号位保留原本的符号；$A$的末位转移到$Q$的符号位上

布斯算法硬件原理流程图.png

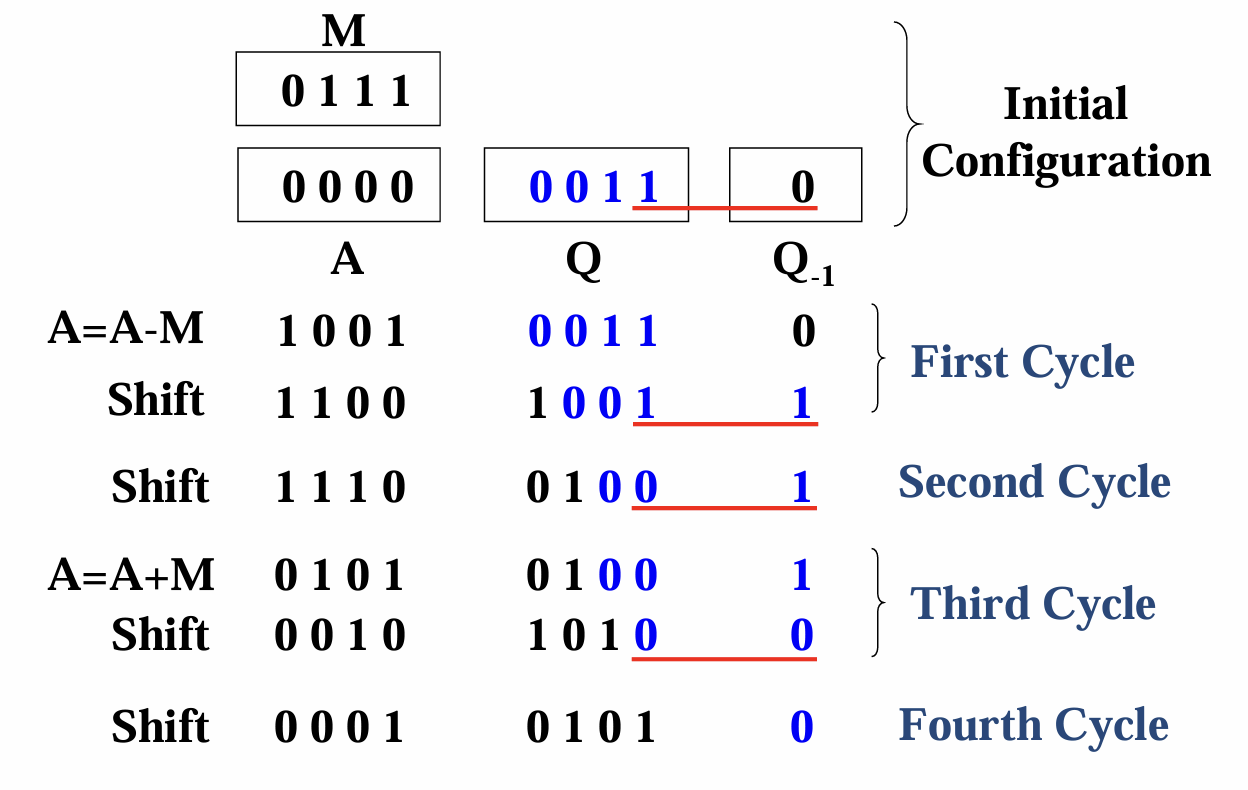
  • 先观察$Q$的末尾和$Q_{-1}$，若组成$10$则进行$A=A-M$，直到变成$01$再进行$A=A+M$的运算

Booth算法乘法器示意.png

  • 最终的运算结果由$A$和$Q$两个寄存器的结果所组成，上图的结果就是$0001\space0101$；下面是另一个例子，其结果为$000100\space000100$

Booth算法乘法器示意2.png

4.4.4 算法优势

  • 可以处理不同符号数的乘法
  • 其通常情况下的运算速度与普通的乘法器相同

五、整数除法运算

5.1 二进制除法

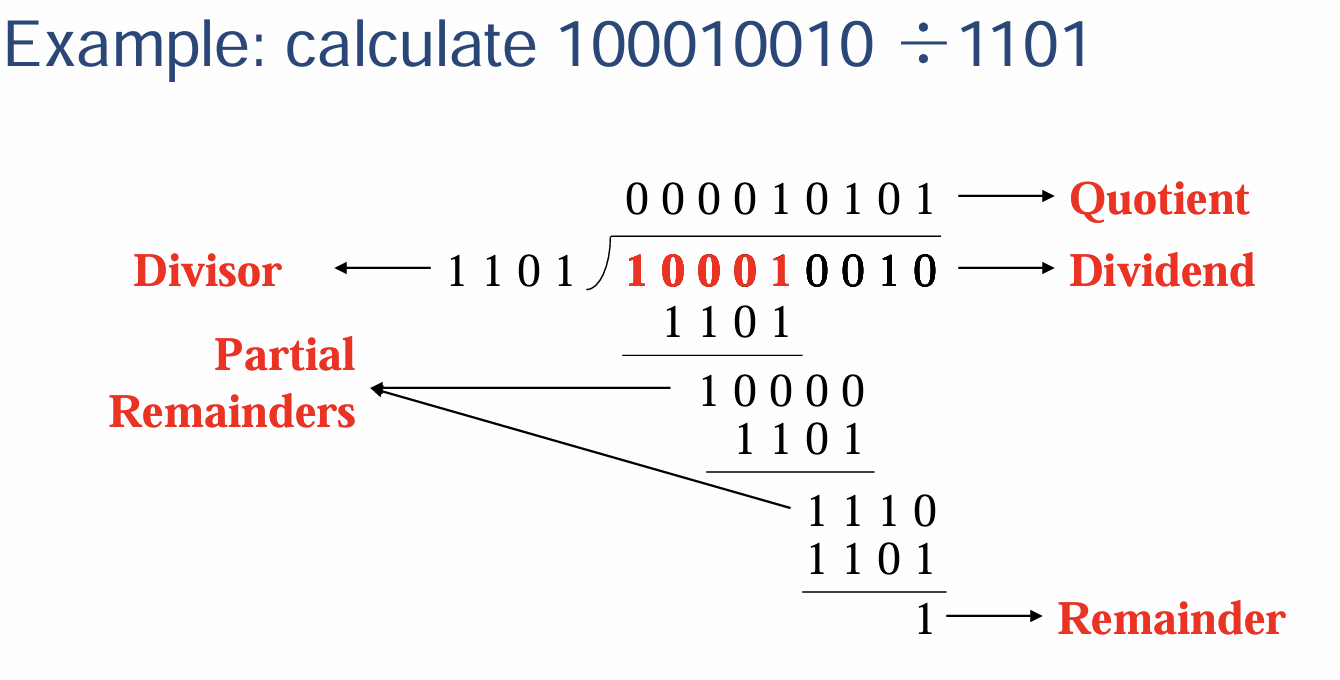
  • 二进制原码的除法和十进制乘法竖式原理一致；减法的竖式运算存在借位（原码减法并不能像补码运算那样取反进行加法），从相邻高位借到本位相当于$2$（由于二进制不存在$2$，所以更严谨点是$1+1$），本位减去了下面的$1$后在本位留下$1$

二进制除法.png

  • 注意图中的术语英文表达：被除数（Dividend）、除数（Divisor）、商（Quotient）、余数（Remainder）、作为中间过程量的部分余数（Partial Remainder）

5.2 恢复余数的除法

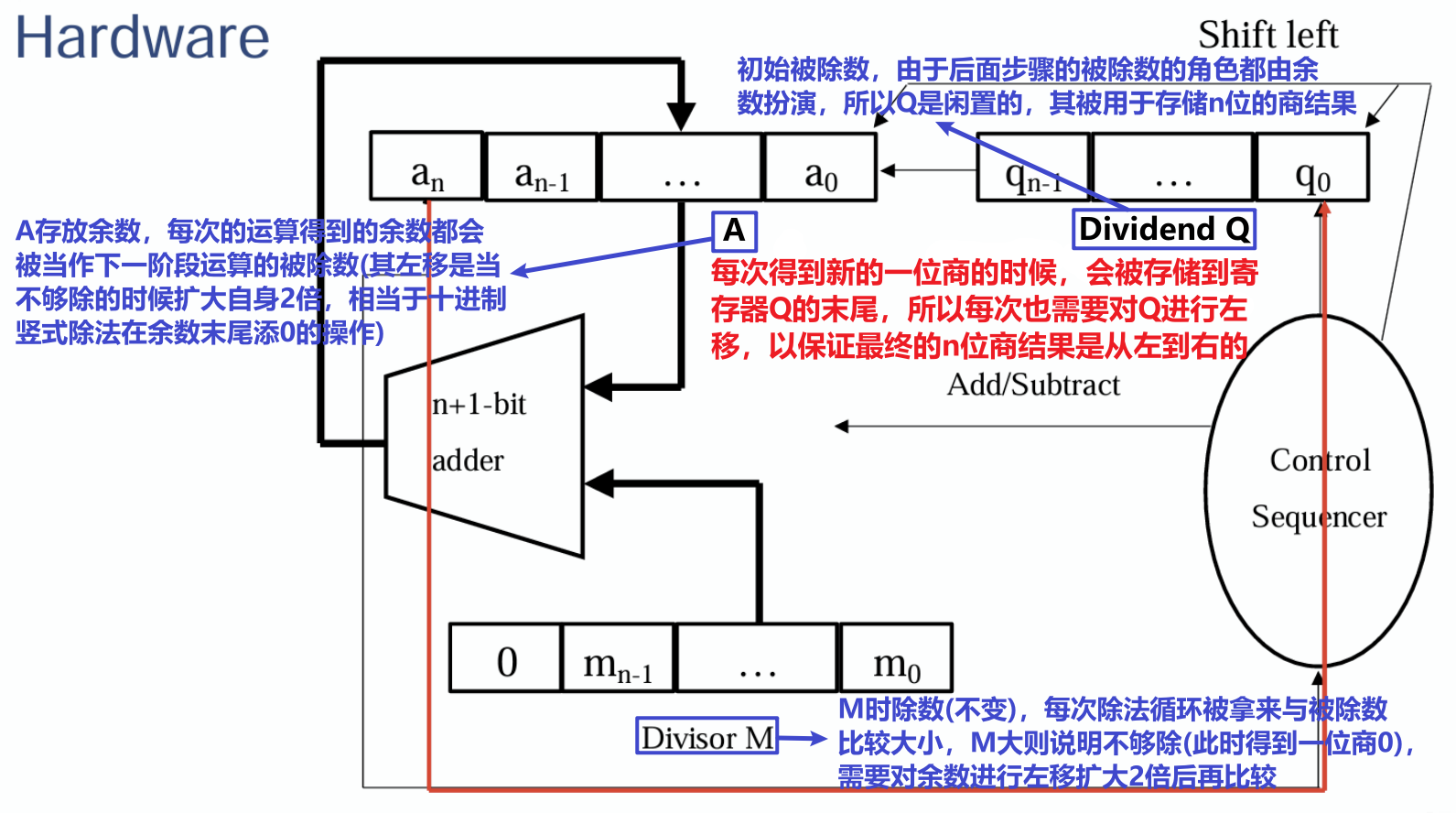
  • 恢复余数的除法（Restoring Division）的硬件示意图及其符号解释如下
    • 寄存器$Q$存储的被除数会发生改变，用于存储运算的结果（商）
    • 寄存器$M$存储的除数由于每次运算都需要用到，故而不会发生改变（与乘法恰好相反）
    • 寄存器$A$则用于存储每次运算产生的余数，此余数被用作被除数参与下一轮运算
    • 除法的每个小步骤中都会得到一位商结果，被存储到$Q$上，最终得到$n$位商

RestoringDivision硬件图.png

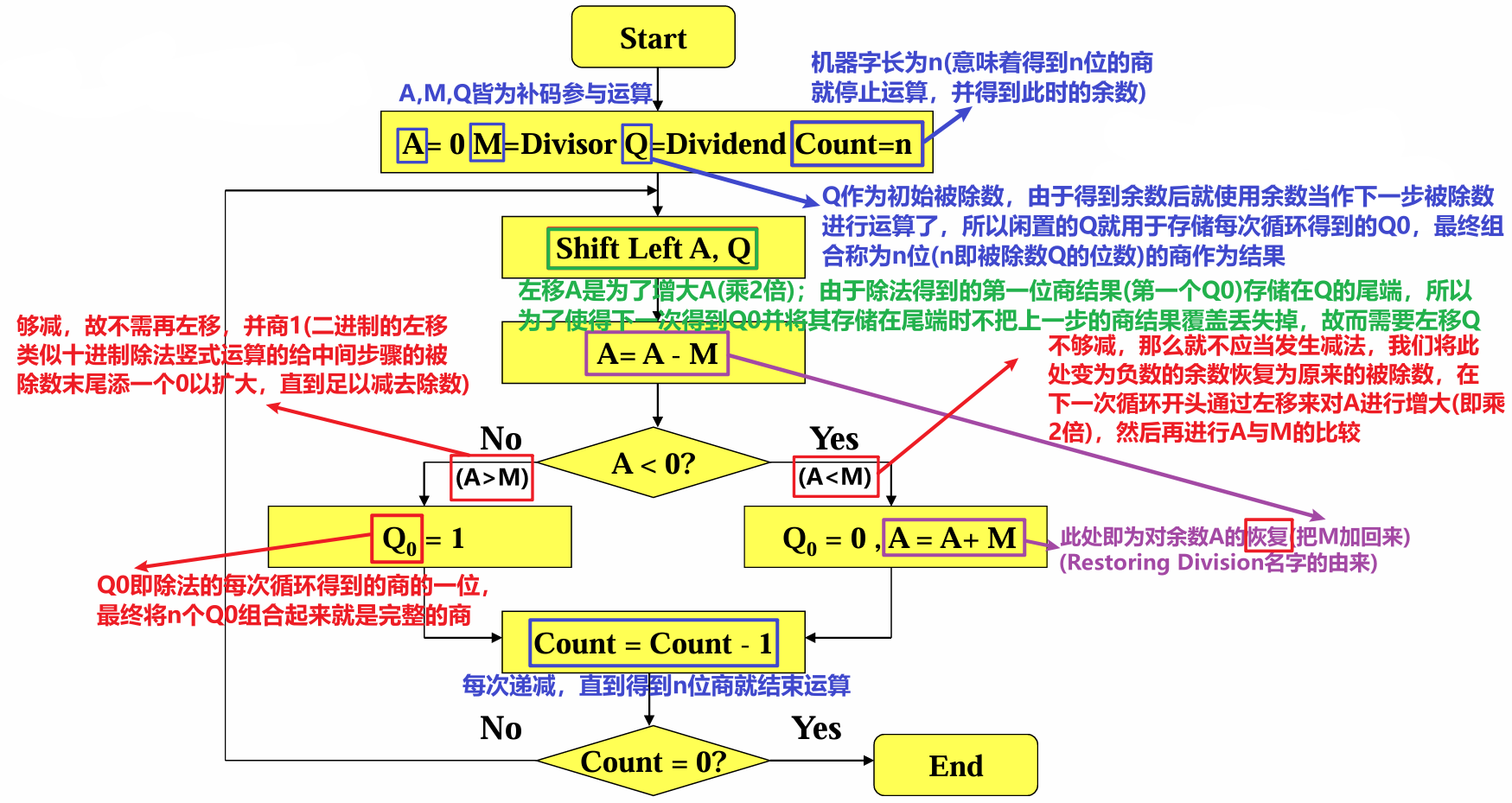
  • 其算法的流程图如下

保留余数的乘法流程图示意.png

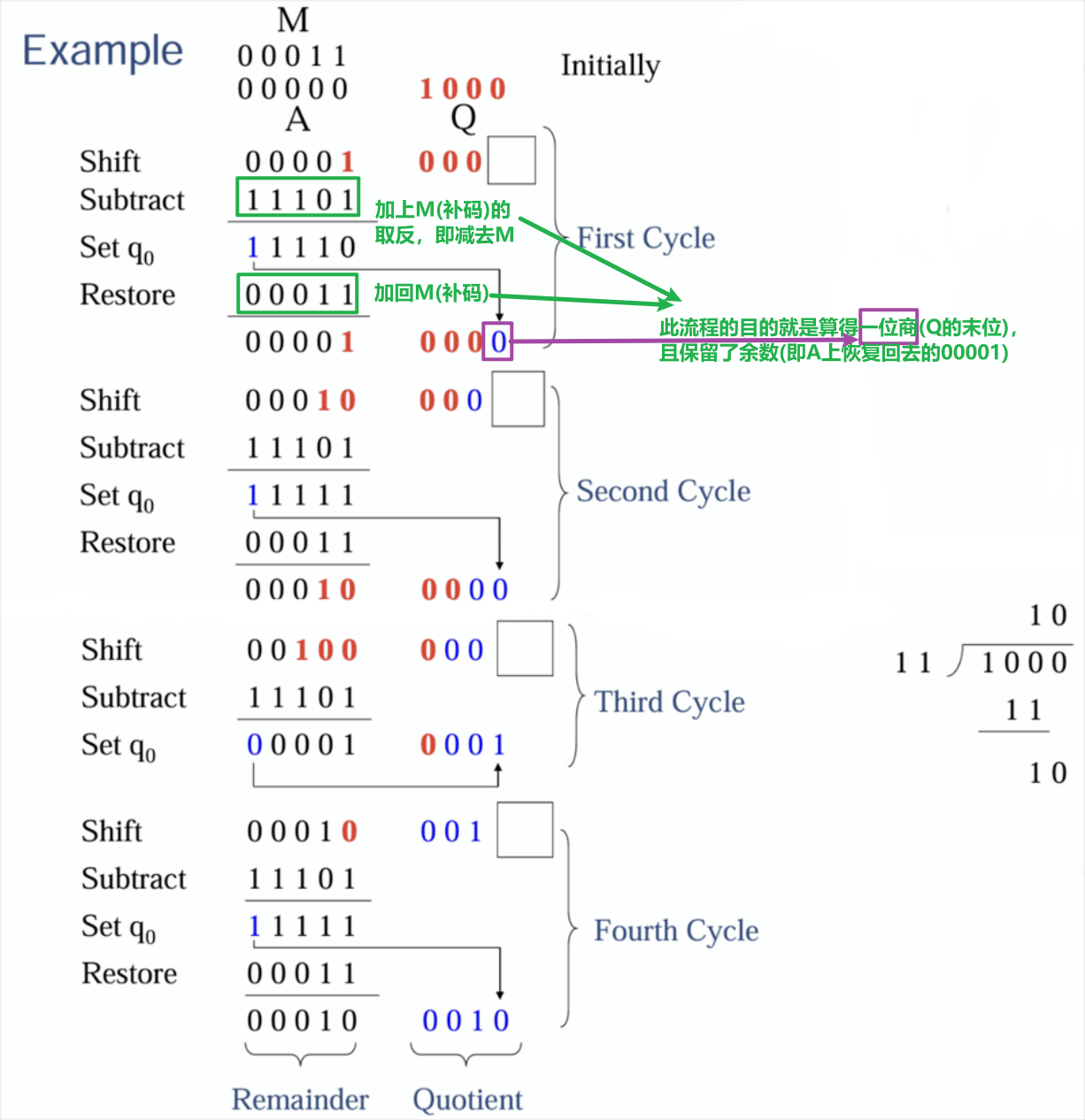
保留余数除法的示例.png

5.3 不恢复余数的除法

  • 在上面恢复余数的除法中，余数$A$每次减去除数$M$后，如果结果为负说明不够减，所以要恢复为原来的余数（即把$M$加回来），然后进行左移扩增（即x2）后再进行够不够减的判断，这几个步骤的数学（临时以Buf存储运算结果，仅作示意含义）表示如下
\[\begin{aligned} & \text{1. 余数减除数：} Buf = A - M \\ & \text{2. 若$Buf$为负：} Buf += M \Rightarrow Buf = A \\ & \text{3. 左移即乘二：} Buf *= 2 \Rightarrow Buf = 2A\\ & \text{4. 再进行相减：} Buf -= M \Rightarrow Buf = 2A - M \end{aligned}\]
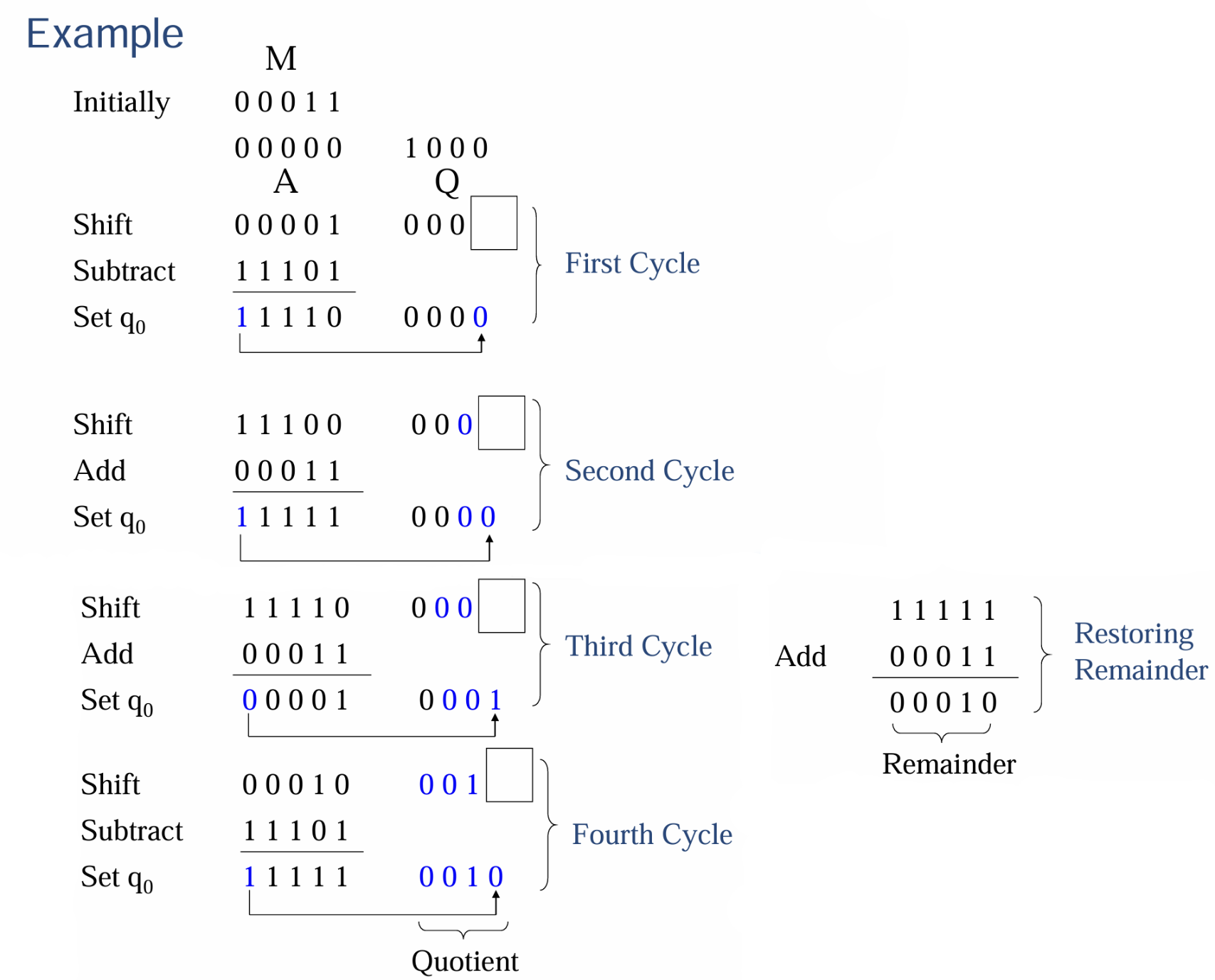
  • 不恢复余数法的意思就是如果得出了$Buf$为负的结论，那么就无需将$Buf$（此时为$A-M$）的数恢复到减去$M$之前（恢复到$A$），即直接计算$Buf = 2A-M$即可，这样就可以省去上述流程中的第2、3步对计算资源的浪费，以加快运算速度
  • 具体怎么计算$Buf = 2A-M$的值呢，将此时为$A-M$的$Buf$左移一位，得到$Buf=2A-2M$，如下图所示，我们只需将其加上一个$M$即可得到$Buf = 2A-M$，然后重复算法判断循环即可

不恢复余数除法的示例.png

六、习题训练

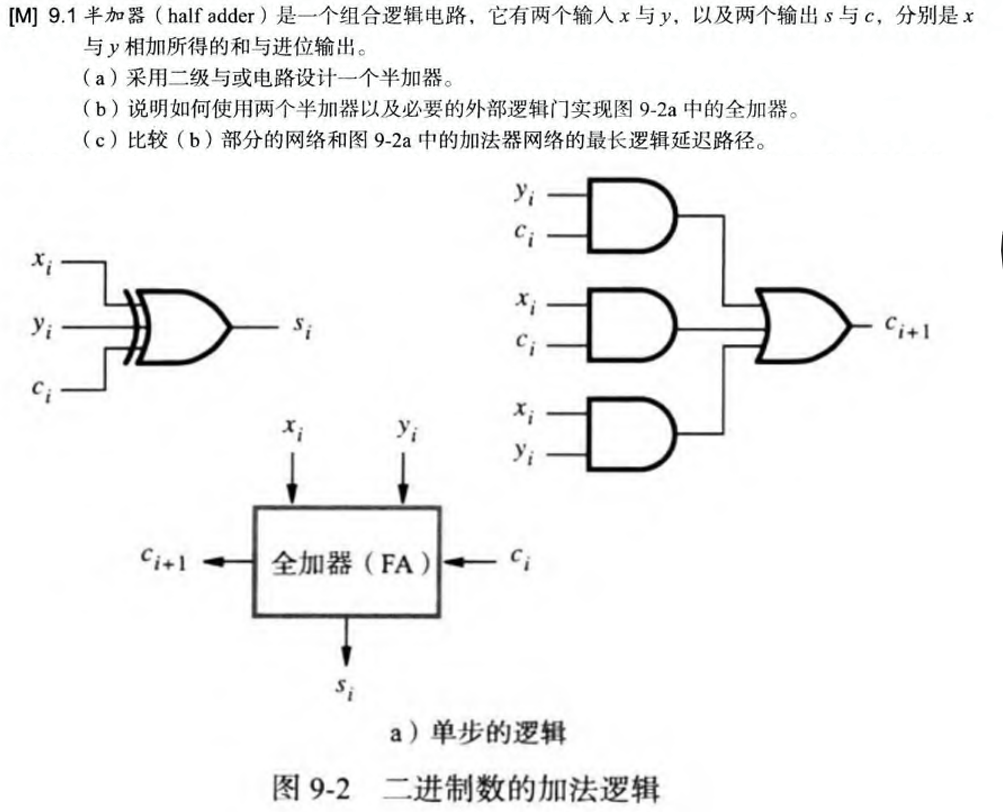
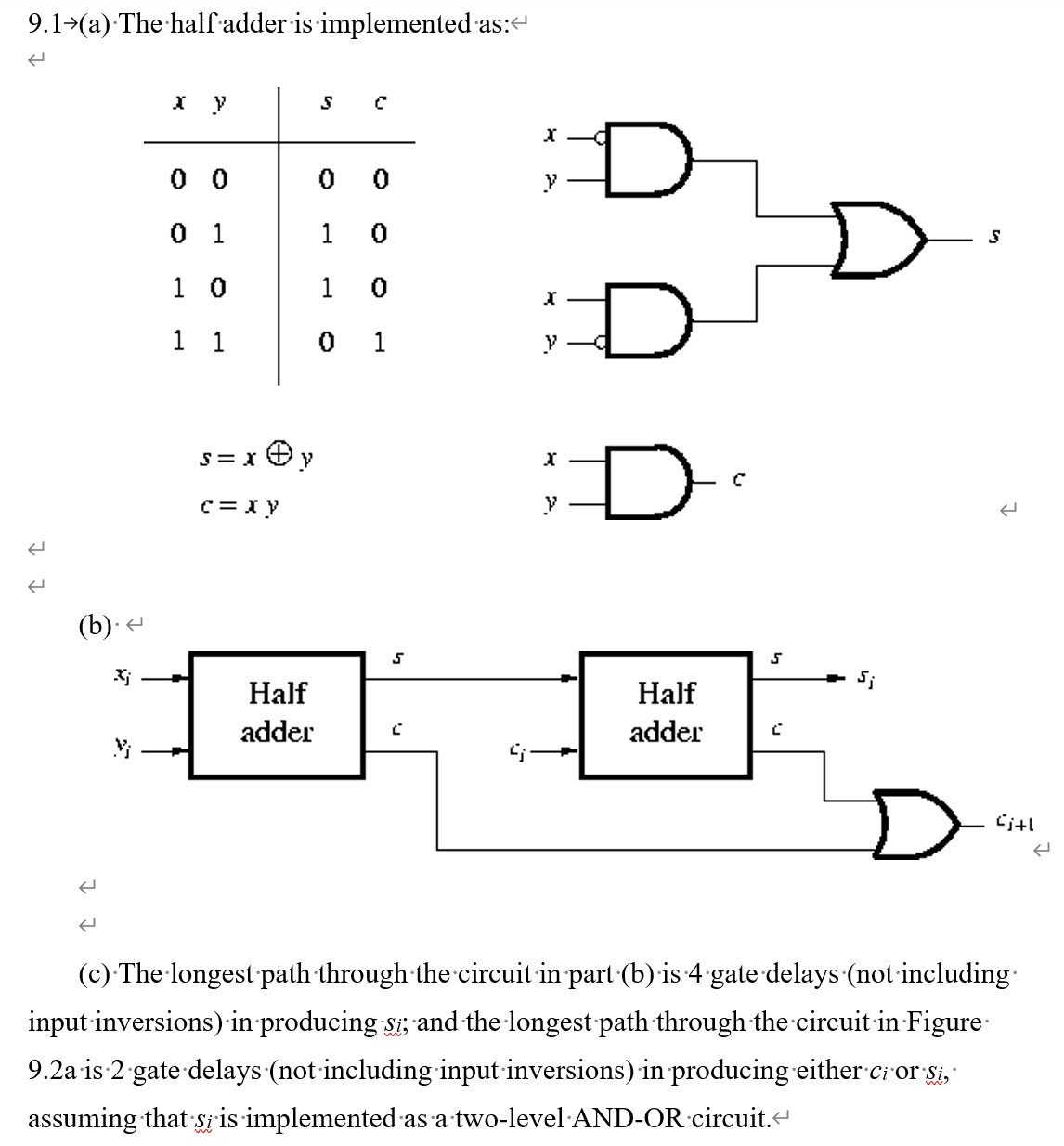
6.1 硬件实现B-Cell

  • 此例题中的门延迟和上面我笔记里研究传播延迟时有所不同，后者将异或门的门延迟视为$T$，此处的异或门是由与门和或门组成的，所以对于传播延迟的分析会所不同（实际上如果我们知道这两处的分析都是不严谨的，应当将所有逻辑门都拆分为最基本的相同逻辑门单元NAND才能严谨地研究传播延迟，所以此处知道意思就行，不必过于深究）

NumberCalculateT1.png

  • 注意下图的异或门被拆分成了最基本的与门和或门（输入处的小圆圈指的是取非），即从$x$和$y$的输入到输出$s$经历的传播延迟是$2T$，从输入到输出$c$经历的传播延迟是$T$
  • 第二问通过两个半加器和一个或门构成一个全加器，从输入$x_i$和$y_i$到输出$s_i$经历了$2T+2T=4T$的传播延迟，从$c_i$的输入到$c_{i+1}$的输出一共经历了半加器的$T$和或门的$T$，一共$2T$的传播延迟（参考行波进位加法器，由于两个数的每位$x_i$和$y_i$都是确定的，所以第一个半加器不需要等待$c_i$的输入即可直接被算出，所以$c_i$一旦被输入，第一个半加器就处于已经输出了$s$和$c$的状态）

NumberCalculateT1Ans.png

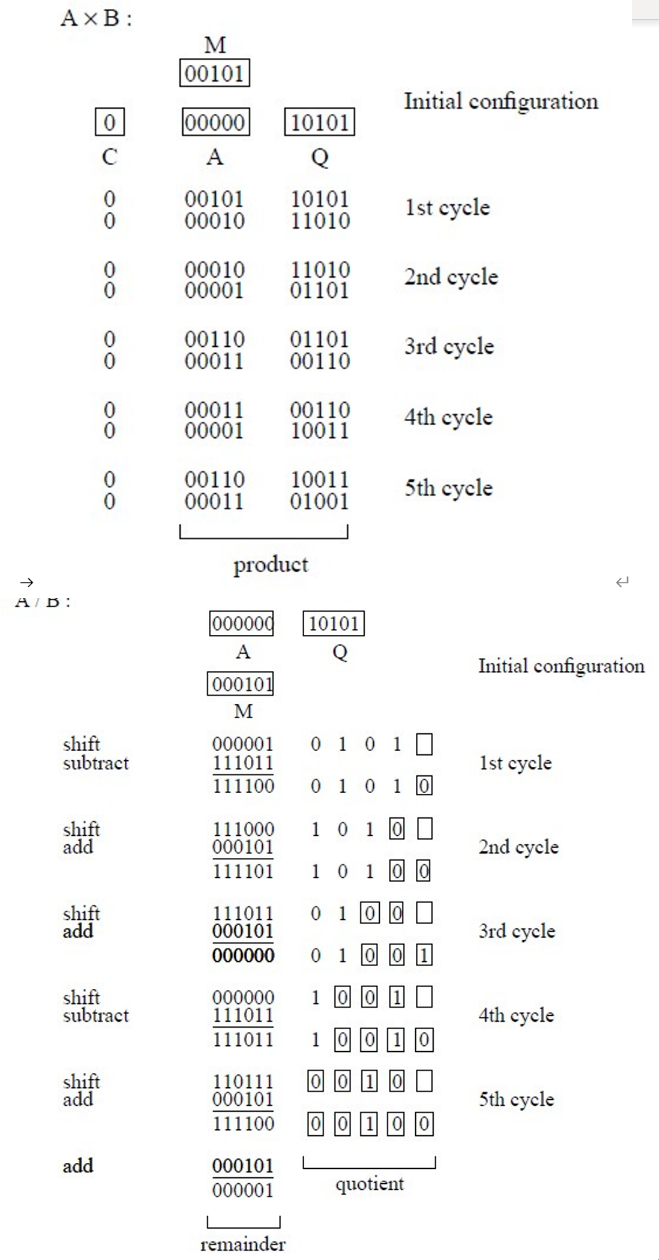
6.2 无符号整数乘除

  • 考察无符号整数的乘除法硬件实现原理

NumberCalculateT3.png

NumberCalculateT3Ans.png

6.3 布斯算法

  • 考察布斯算法（有符号整数的乘法）的直接应用

NumberCalculateT2.png

NumberCalculateT2Ans.png

学科笔记, 组成原理
组成原理 数字电路
本文由作者按照 CC BY-NC-SA 4.0 进行授权