算法图理论的基本概念介绍

一、图的概念

1.1 无向图

1.1.1 顶点与边

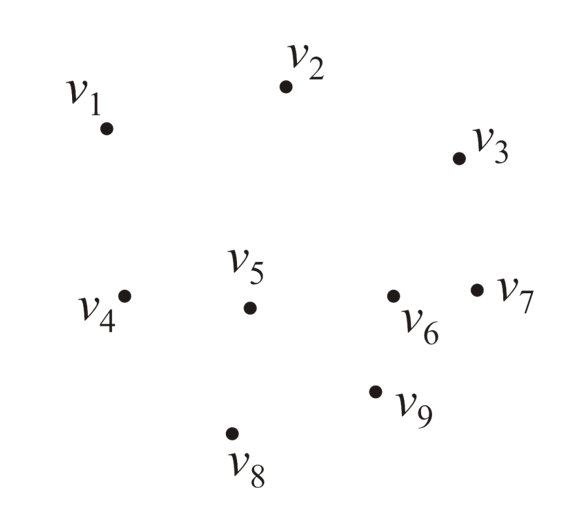
• 图（Graph）包含顶点（Vertex）和边（Edge），先定义顶点的集合$V$

\[V=\{v_1,v_2,...,v_n\}\]

• 集合$V$内的顶点元素数表示为$|V|=n$，例如下图中的$|V|=9$

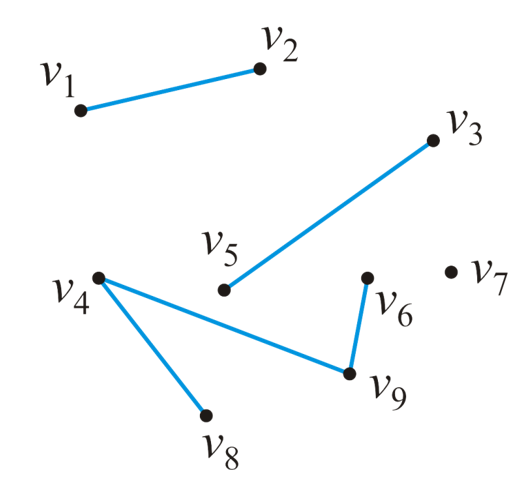
• 对于无向图（Undirected Graph），其各顶点之间存在的关系是无向的，这些关系表现为连线两个顶点形成的边，例如参照下图，可以定义图内的所有边组成的集合为

\[E=\{\{v_1,v_2\},\{v_3,v_5\},\{v_4,v_8\},\{v_4,v_9\},\{v_6,v_9\}\}\]

• 集合$E$内的元素就是$V$内顶点间的无向关系，记为无序二元组${v_m,v_n}$，元素数量表示为$|E|$，例如下图中的$|E|=5$

• 我们如果不考虑${v_m,v_m}$的意义，则一个顶点数为$n$的无向图的$|E|$最大值为

\[C^2_n=\frac{n(n-1)}{2}\]

1.1.2 顶点的度数

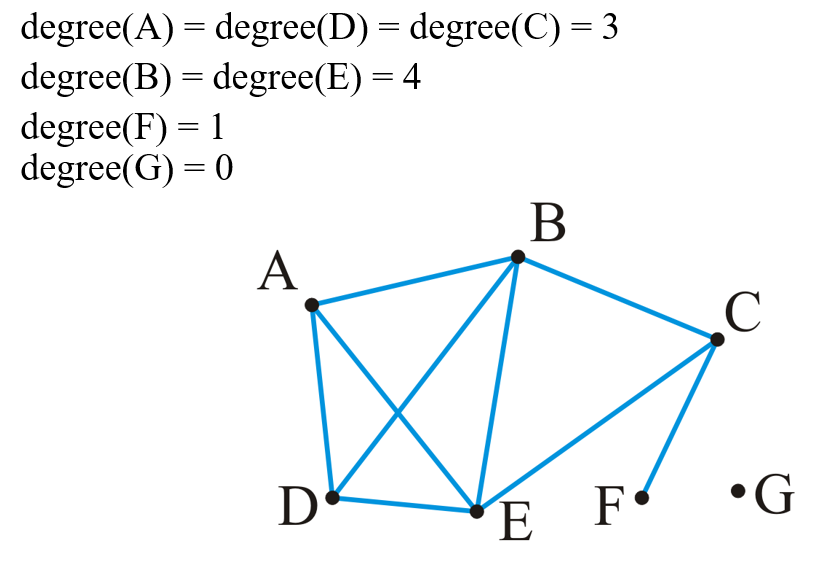
• 对于图中的一个顶点，邻接顶点（Adjacent Vertices）的个数（即与该顶点间存在关系的顶点的个数）就是该顶点的度数（Degree）

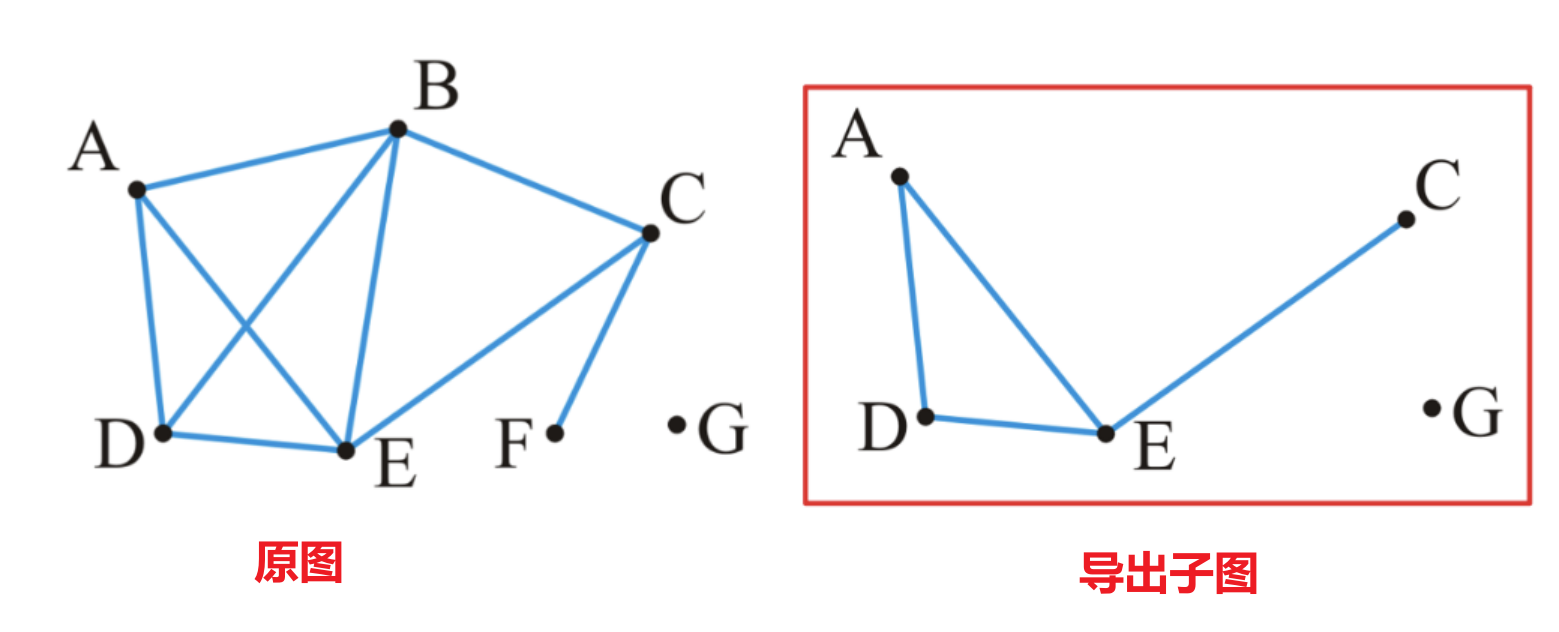
1.1.3 子图与导出子图

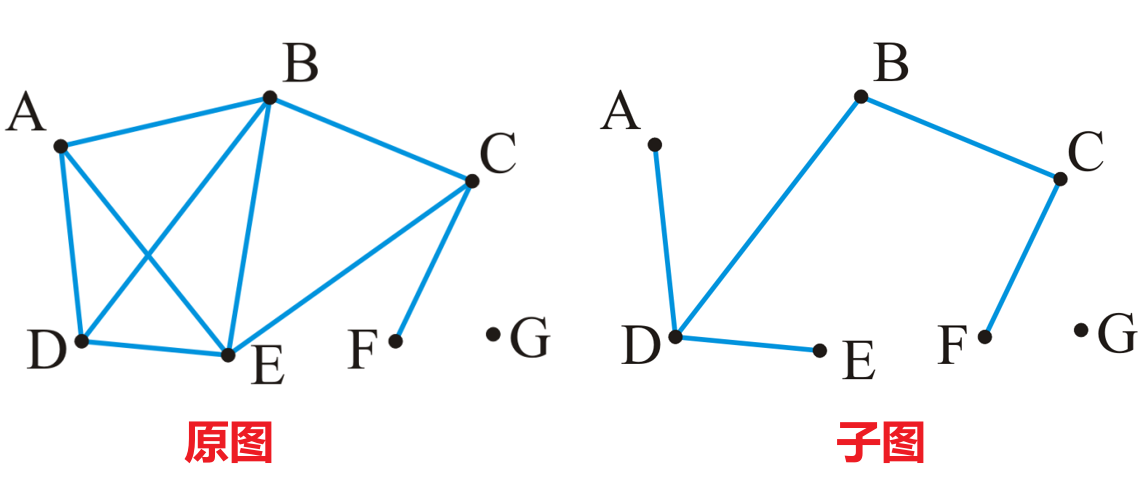
• 一个图$G=(V,E)$的子图（Subgraph）表示为$G’=(V’,E’)$，其包含原图中的部分顶点$V’\subset V$，以及这部分顶点间的部分关系$E’\subset E$

• 一个图$G$的顶点导出子图（Vertex-Induced Subgraph）简称导出子图（Induced Subgraph）
  • 其顶点集同样是原图顶点的任意一个子集$V’\subset V$
  • 与子图不同的是，导出子图的$E’$必须包含原图$G$中关于$V’$内顶点的所有关系，不能遗漏
• 如下图中，如果右侧图中的关系$(A,E)$被舍弃了，那么其就不是导出子图了，而是普通子图

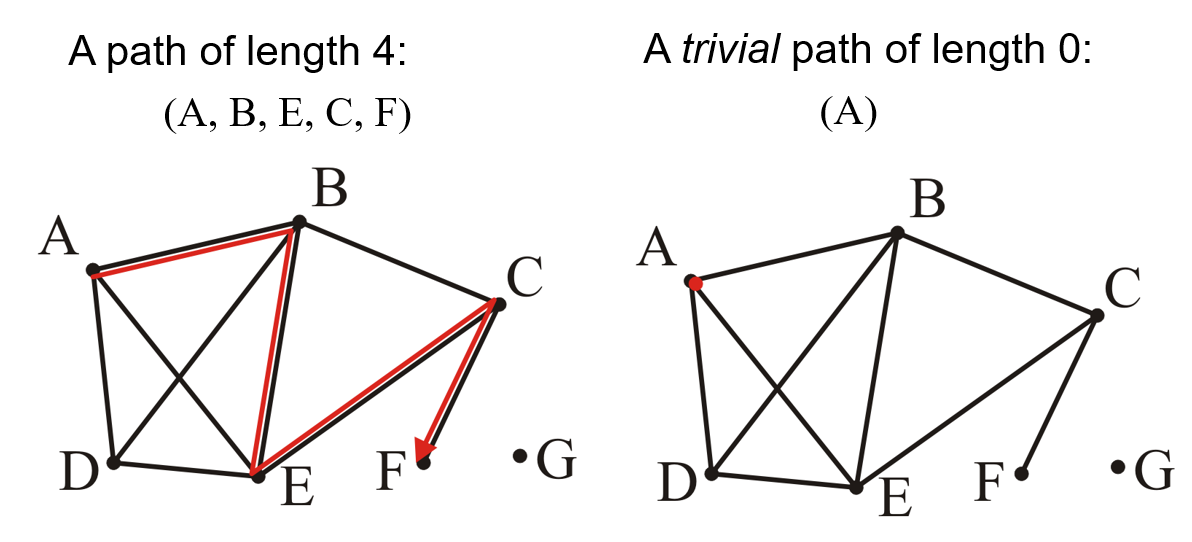
1.1.4 路径

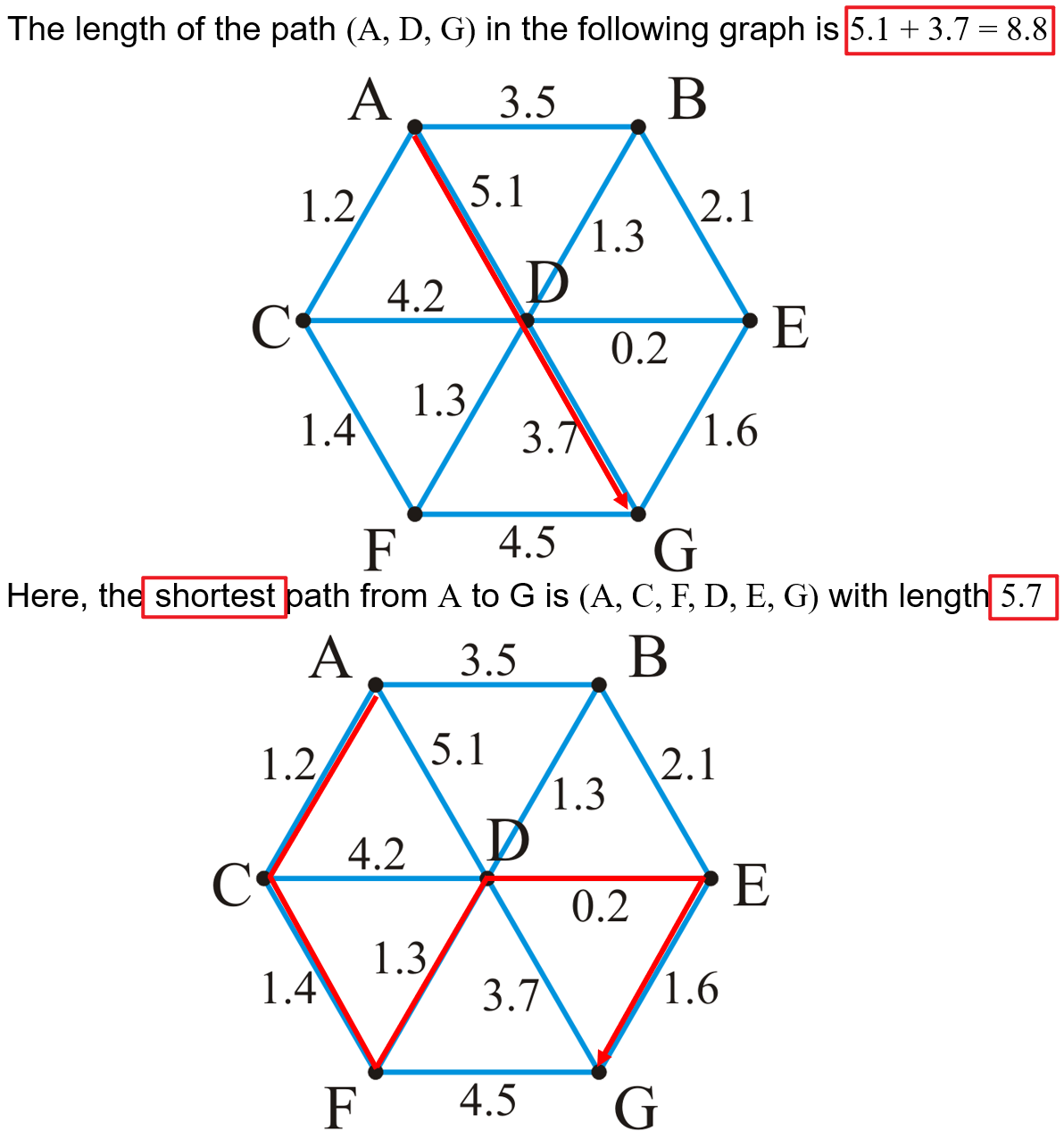
• 一个图中的路径（Path）指的就是一个有序的顶点序列$(v_0,v_1,…v_k)$
  • 其中任意相邻的两个顶点之间必须存在关系，即${v_{i-1},v_i}$必须是图中存在的边
  • 这样的一个序列构成了从顶点$v_0$到顶点$v_k$间的路径，长度为$k$（即路径顶点数-1）

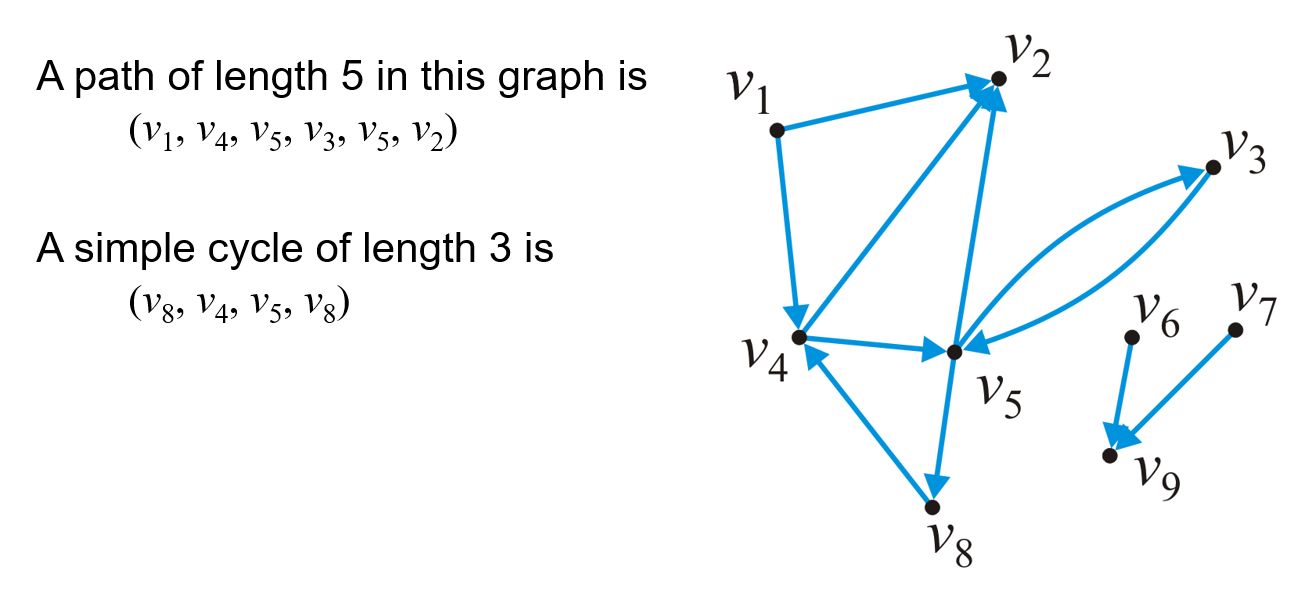
• 如果路径中没有重复的顶点，则称该路径为简单路径（Simple Path）
• 如果路径的首尾顶点相同，则称该路径为回路/环/圈（Cycle）

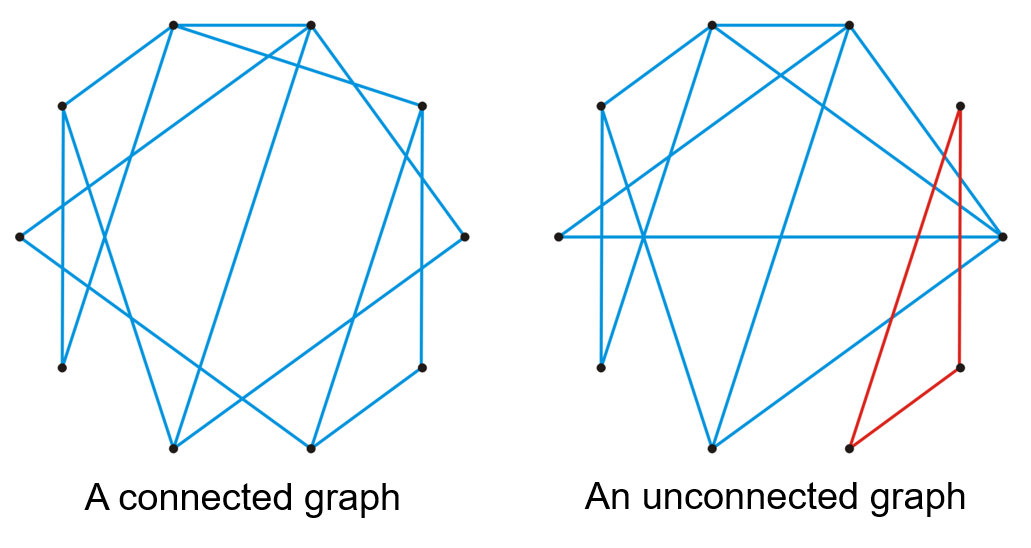
1.1.5 连通性

• 如果存在一条以某两个顶点为首尾的路径，则这两个顶点被称为是连通的（Connected）
• 如果一个图内的所有顶点间都是连通的，则该图也被称为是连通的

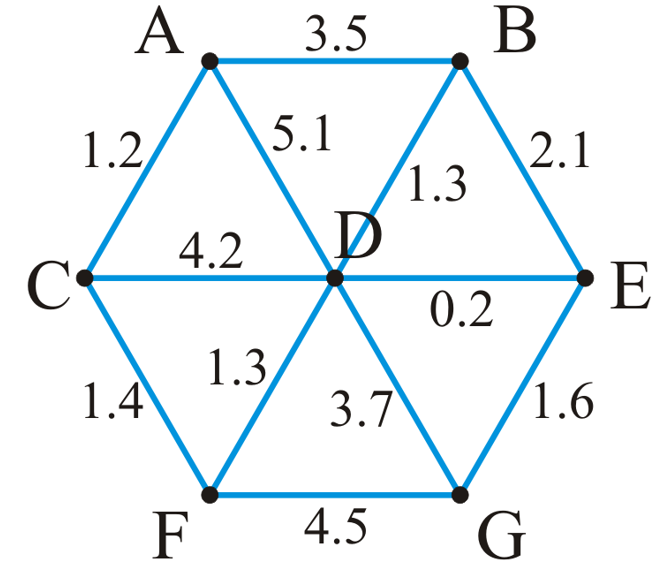
1.1.6 权重

• 如果图内顶点之间的边全都被附加了一个权重（可以用于表示距离、花费等概念）数值，则这类图称为加权图（Weighted Graph）

• 对于加权图，其路径的长度就是路径上的边的权重之和

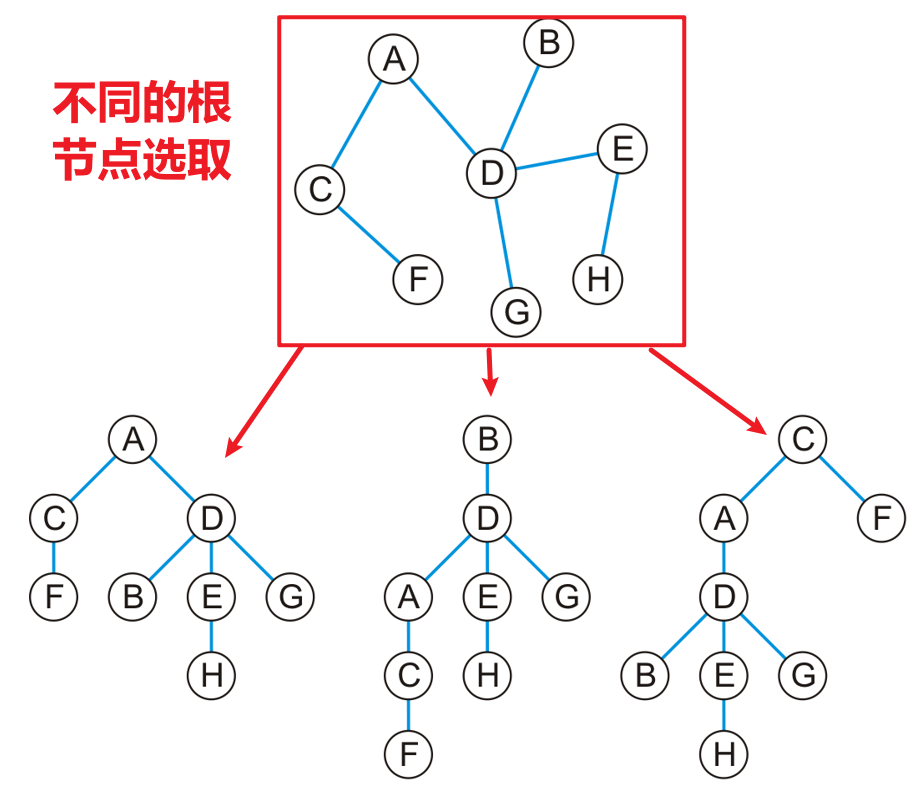
1.1.7 图与树的关系

• 若图中的所有顶点两两之间只存在唯一路径连接，表现为$|E|=|V|-1$且无环（Acyclic），则该图就可以表示为一个树结构

• 具体的表示方式为：随意选取一个顶点作为树的根节点，然后该顶点的所有邻接顶点作为该根节点的子节点，对子节点递归地进行同样的操作

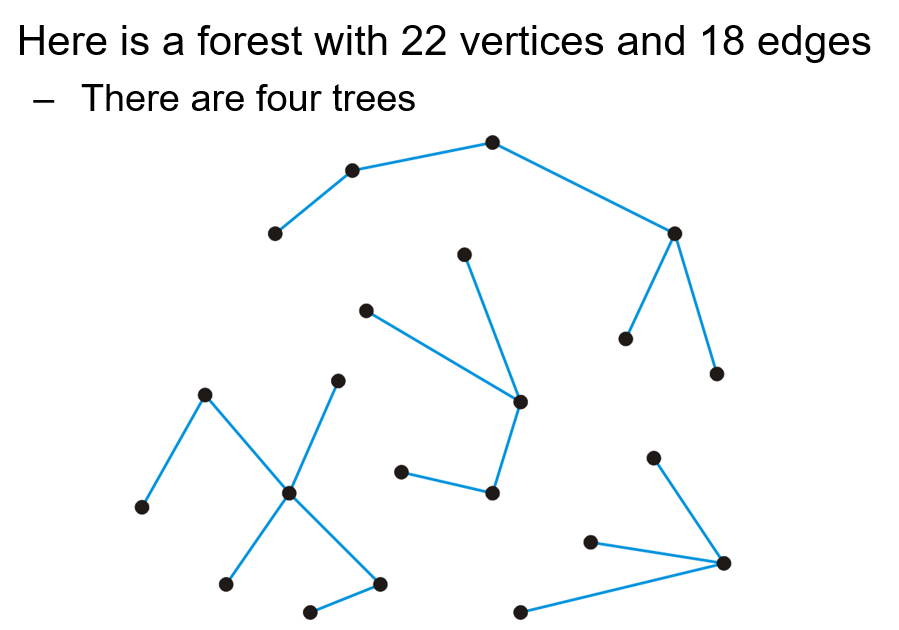
1.1.8 森林

• 任意一个无环（Acyclic）的无向图被称为森林（Forest），森林必定满足$|E|<|V|$，森林中至少包含一棵能表示为树的子图，森林中的树棵树等于$|V|-|E|$，移除任意一条边都会增加一棵树

1.2 有向图

1.2.1 有向边

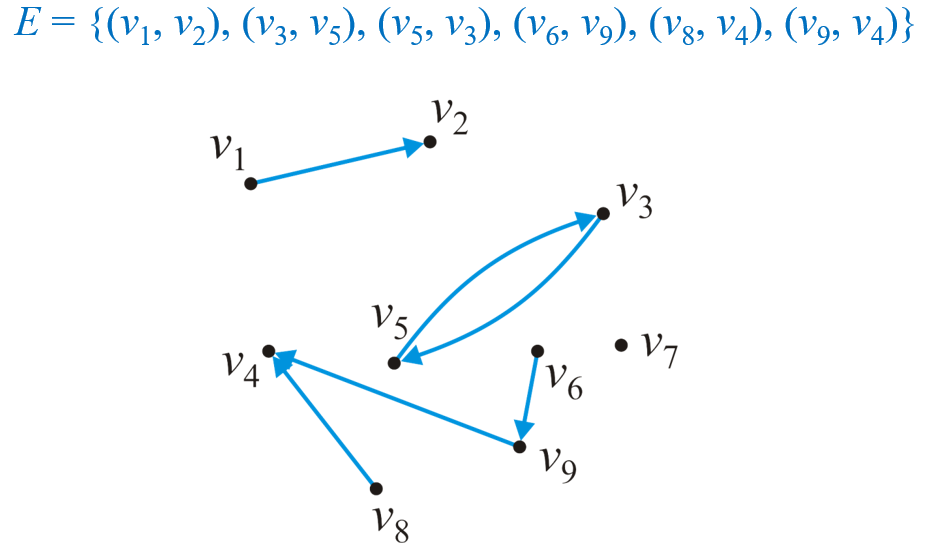
• 在有向图（Directed Graph）中，$E$中所有的边均为有序二元组$(v_m,v_n)$，而非无向图中的无序二元组${v_m,v_n}$，这意味着$(v_m,v_n)$不等于$(v_n,v_m)$

• 如果不考虑$(v_m,v_m)$，则顶点数为$n$的$|E|$的最大值为

\[2C^2_n=n(n-1)\]

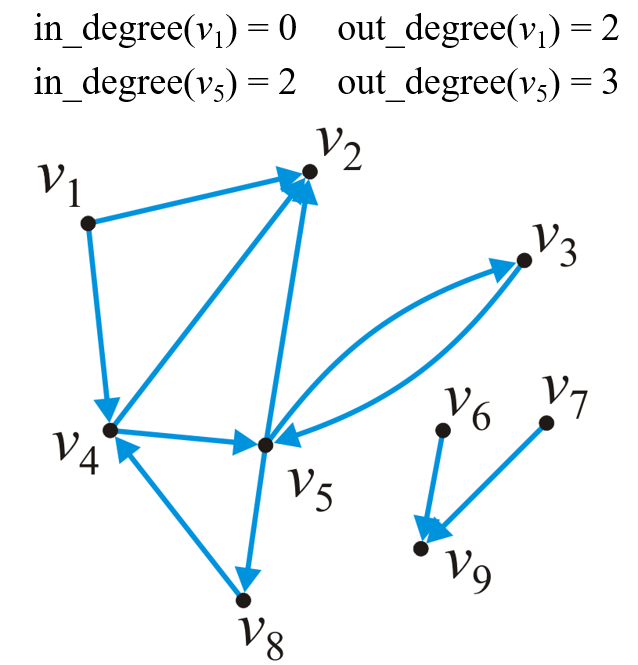
1.2.2 入度与出度

• 对应无向图中的度数，有向图中顶点与顶点间的关系是有向的，则度数也相应地被分为入度（In Degree）和出度（Out Degree）

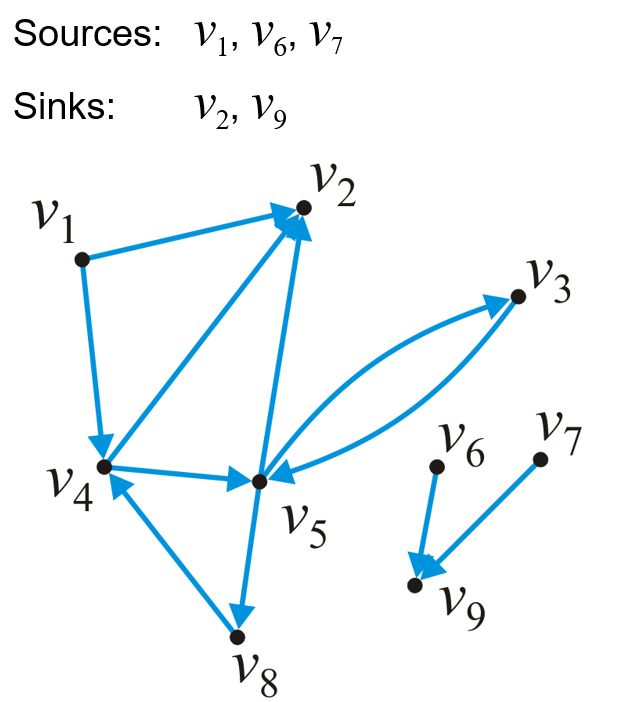
• 其中所有入度为$0$的顶点称为源点（Source），所有出度为$0$的顶点称为汇点（Sink）

1.2.3 路径与DAG

• 有向图中的考虑方向的路径$(v_0,v_1,…,v_k)$中，任意相邻两顶点间的关系$(v_{i-1},v_i)$必须存在，至于关系$(v_i,v_{i-1})$存在与否对该路径并无影响

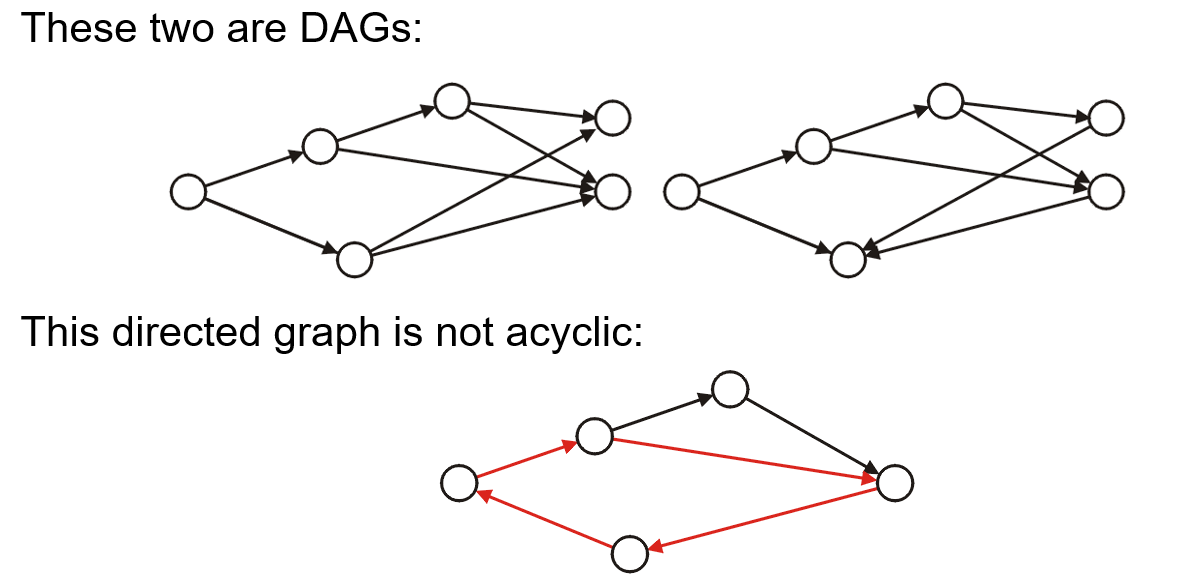
• DAG（Directed Acyclic Graph）指的是无环有向图，该类图可被用于处理依赖关系等场景（如包管理、高级语言编译等）

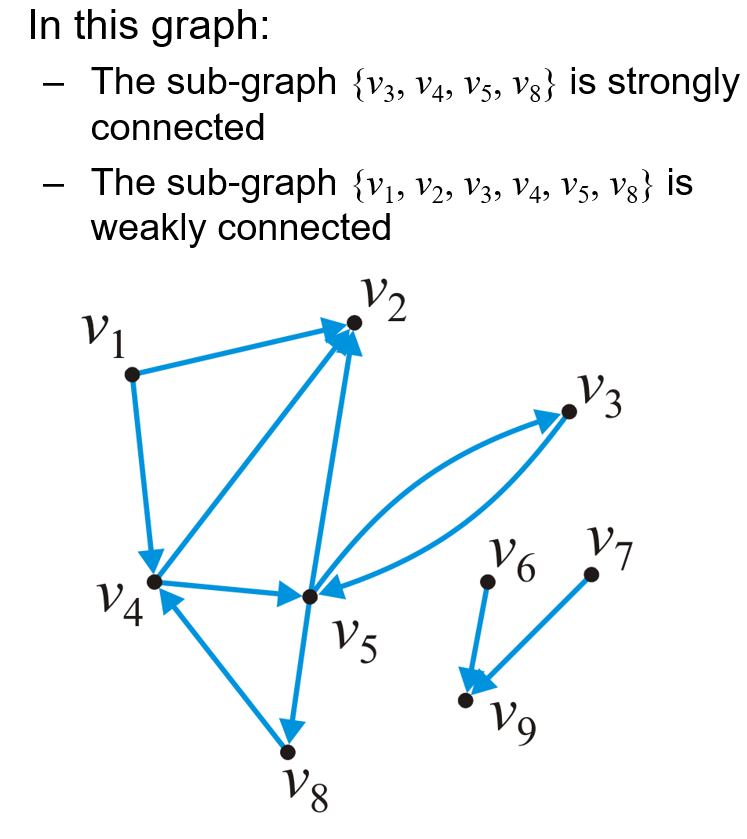
1.2.4 强弱连通性

• 若有向图中存在一条从$v_i$到$v_j$的考虑方向的路径，则这两个定点是连通的，对于一个有向图来说
  • 若图中任意两顶点都能被考虑方向的路径连通，则该图是强连通的（Strongly Connected）
  • 若图中任意两点都能被不考虑方向的路径连通，则该图是弱连通的（Weakly Connected）

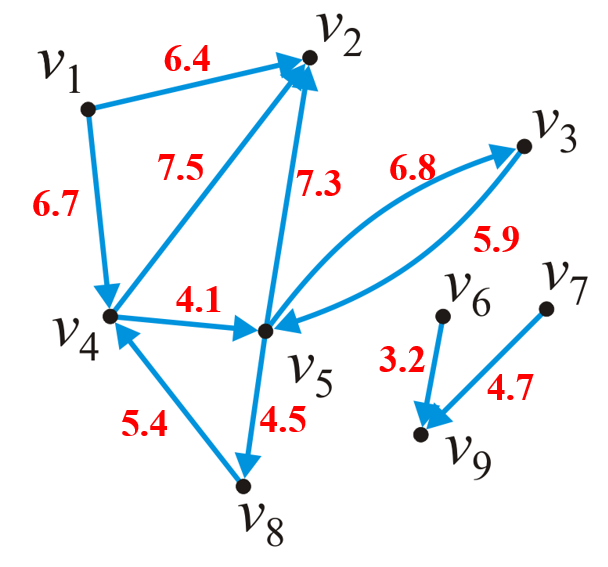
1.2.5 权重

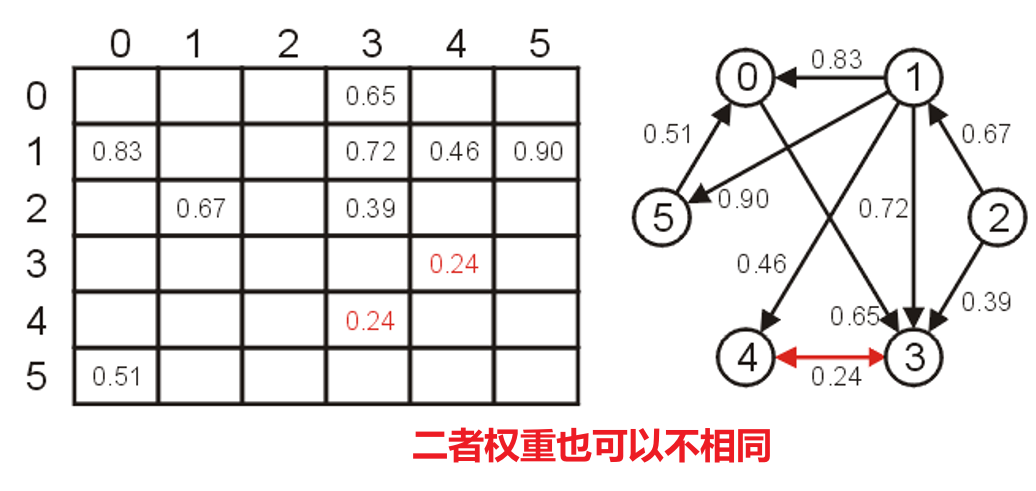
• 有向图中的权重与无向图中的概念基本一致，但前者中$(v_m,v_n)$的权重能和$(v_n,v_m)$的不同

二、图的存储

问题在于如何存储图中的边这样的邻接关系（Adjacency Relations）

2.1 二元关系列表

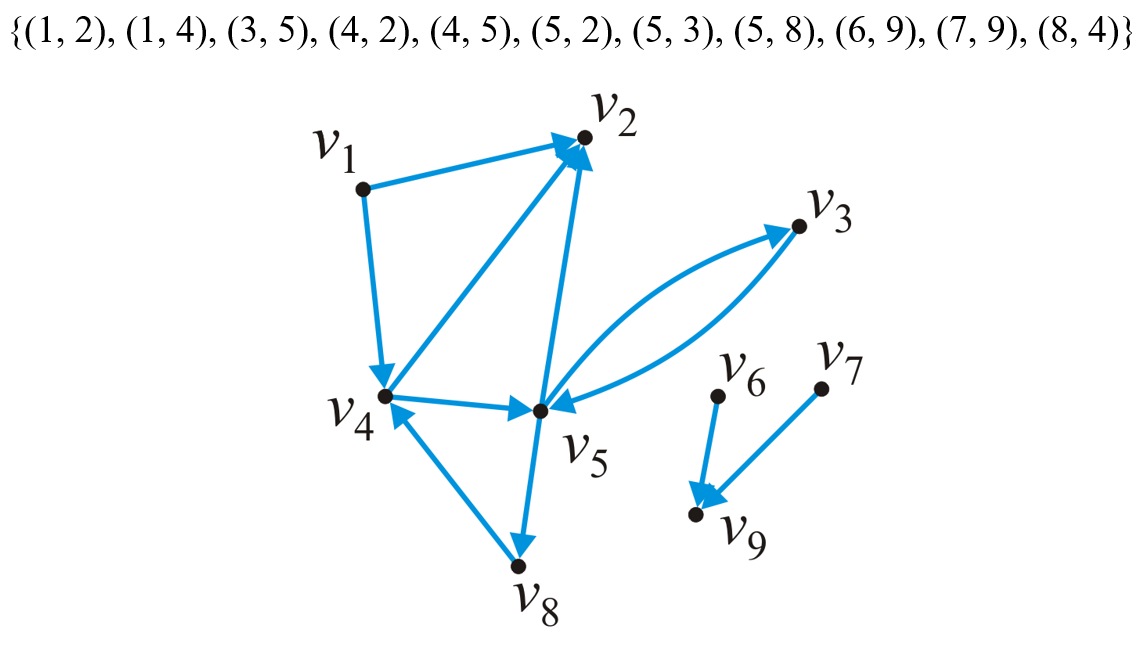
• 二元关系列表（Binary-Relation List）结构以有序二元组作为元素来存储有向图的所有有向边

• 这种方式需要使用$O(|E|)$的空间复杂度来存储列表，遍历该列表找到某个顶点的所有临界顶点的时间复杂度为$O(|E|)$，确定两个顶点是否相邻也需要遍历列表的$O(|E|)$的时间复杂度

2.2 邻接矩阵

2.2.1 实现逻辑

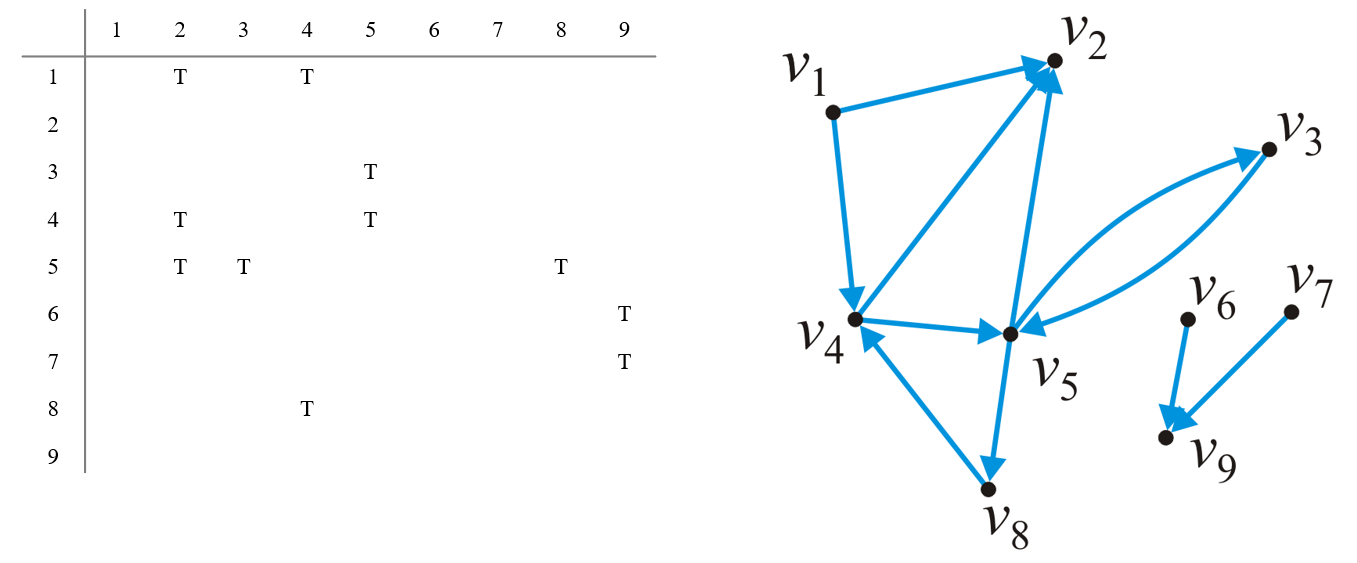
• 可以采用邻接矩阵（Adjacency Matrix）的方式表示一个有向图的所有有向边，矩阵的行和列都指代图中的顶点，$(i,j)$位置上用$1$和$0$表示该关系是否存在
• 这种方式需要更大的$O(|V|^2)$内存空间，查找一个顶点的所有邻接关系需要遍历行列的$O(|V|)$时间复杂度，但查找两个顶点间是否存在邻接关系则仅需$O(1)$的时间复杂度

• 若是加权有向图，则可将矩阵中的对应关系处的$1$改为权重值

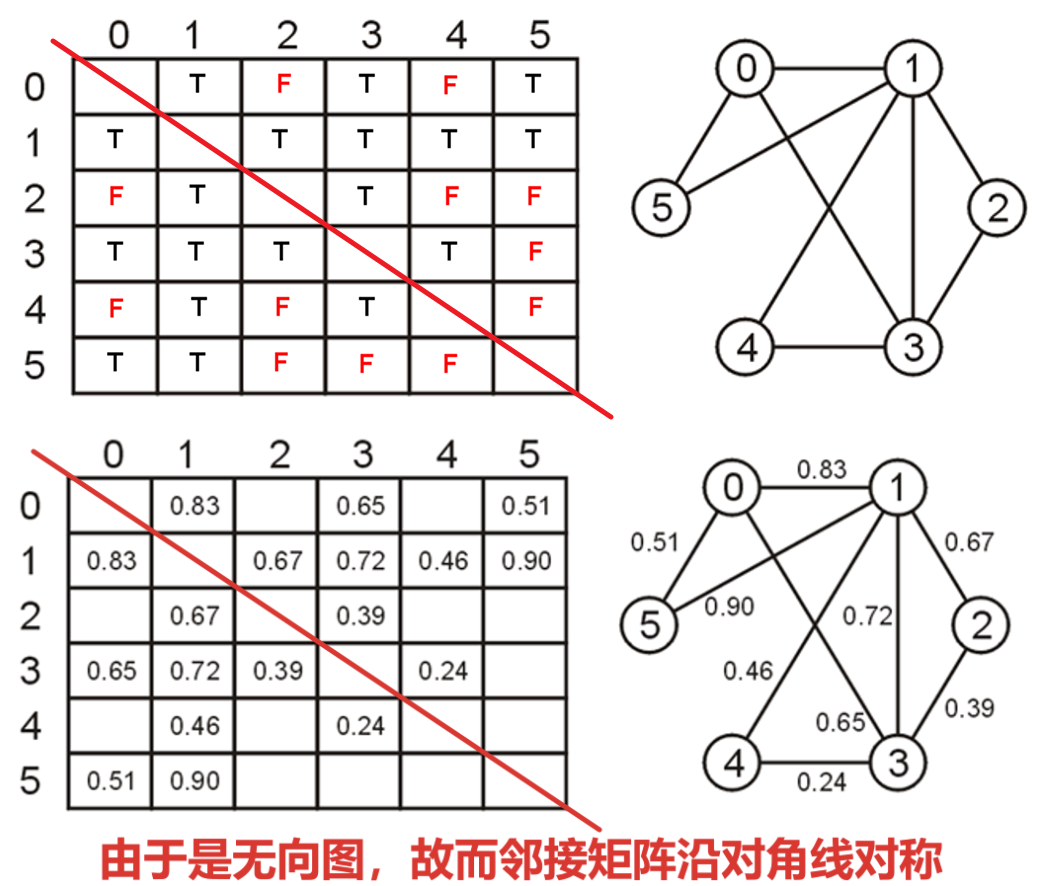
• 不论加权与否，无向图都同样能用邻接矩阵表示，但这样会造成空间的浪费，因为有一半的矩阵空间是重复的信息

• 使用邻接矩阵时，除非顶点与顶点间全部都存在关系，那么矩阵中就一定存在空间的浪费（为解决此问题，可采用邻接列表的实现方式）
  • 如果邻接矩阵中非初始值的项占所有项的不到$5$%，则称该矩阵是稀疏的（Sparse）
  • 如果邻接矩阵中非初始值的项占所有项的超过$25$%，则称该矩阵是密集的（Dense）

2.2.2 代码实现

• 可使用double**维护一组double*数组作为矩阵，或使用std::vector<std::vector<T>>也可

//比如图中有16个顶点，则需要一个16*16的邻接矩阵
size_t N = 16;

//声明矩阵的N个行
double** matrix = new double*[N]

//声明每行矩阵的的N个列
for (size_t i = 0; i < N; ++i)
	matrix[i] = new double[16];

//销毁时先循环delete[]每行matrix[i]的每列，再delete[] matrix

• 对于加权图，其邻接矩阵中不存在关系的位置，我们可以用$0$、负数、无穷大来占位，具体使用什么需要具体问题具体分析（一般使用无穷），而对于不加权的图直接使用false即可

2.3 邻接列表

2.3.1 实现逻辑

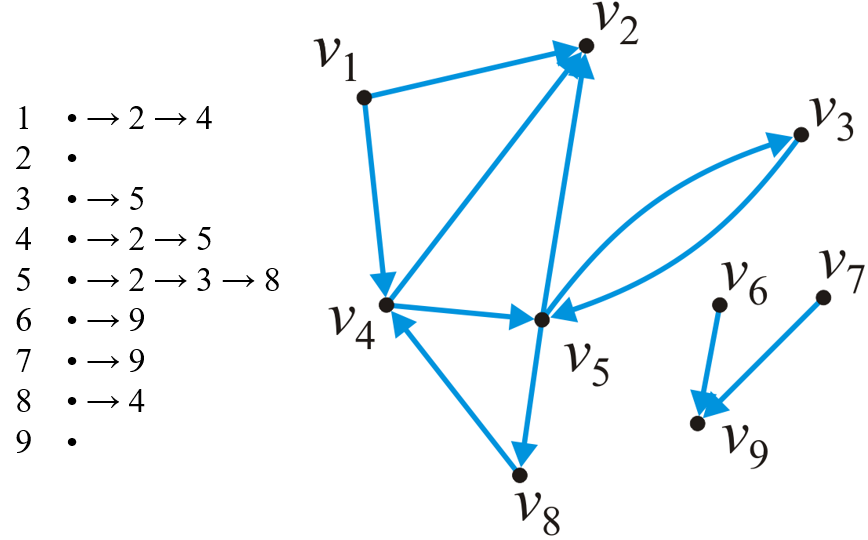
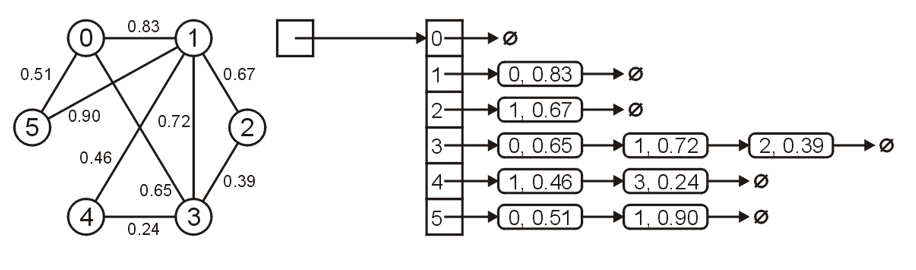
• 邻接列表（Adjacency List），即在存储所有顶点的时使用链表将其指向（在有向图中此处的指向就是顺序关系，在无向图中则仅仅是相邻）的顶点记录下来，如下图所示
• 这种实现需要$O(|V|+|E|)$的空间复杂度，确定两顶点间是否存在邻接关系以及确定一个顶点的所有邻接顶点的时间复杂度平均都为$O(\frac{|E|}{|V|})$

• 对于加权的图来说，则需要改换链表节点为存储(size_t idx, double weight)的数对，其中正整数表示指向特定顶点的索引，浮点数则代表权重，如下图的加权无向图所示

• 无向图的邻接列表中对于相同两个顶点间的关系无需存储像邻接矩阵那样存储两次

2.3.2 代码实现

• 待补充

三、图的搜索

3.1 关于搜索

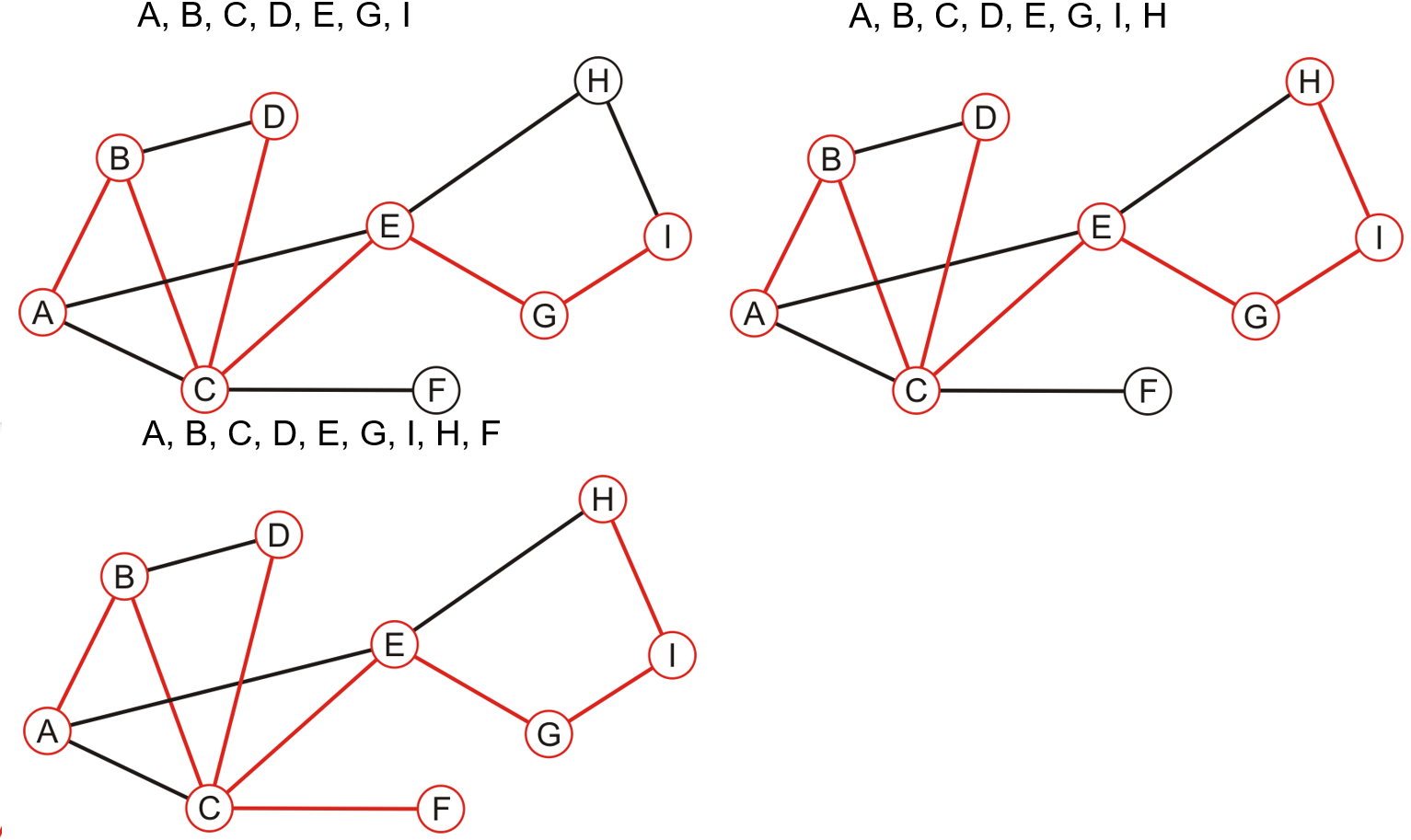
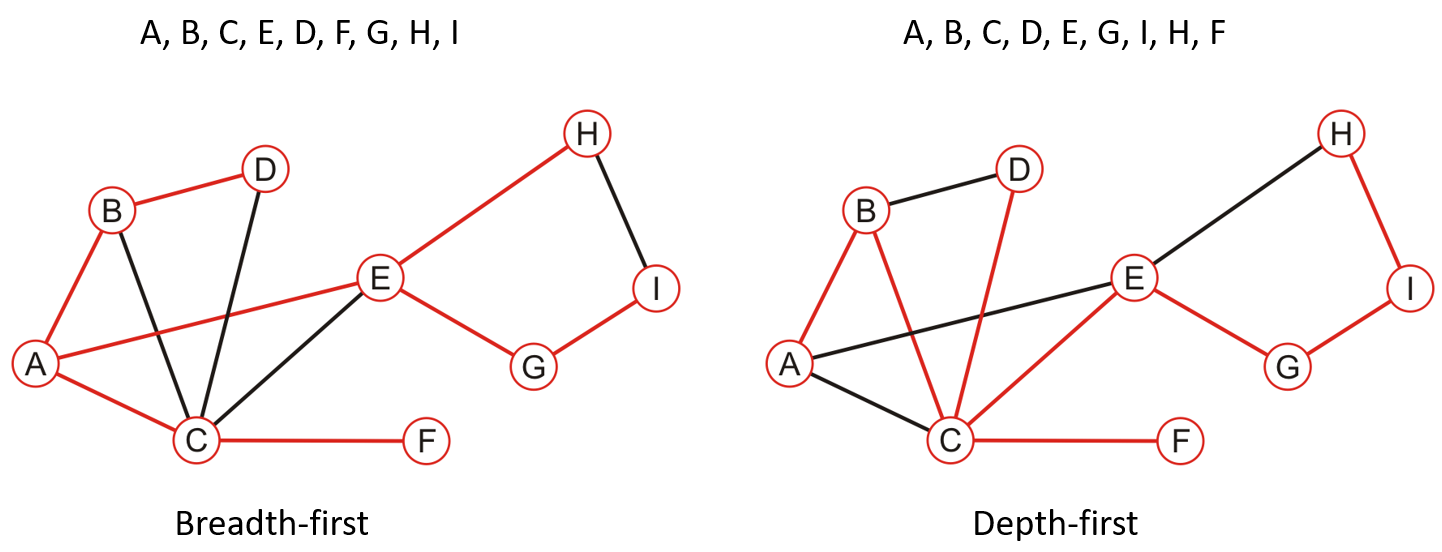
• 图的遍历（Traversal）一般称为搜索（Search），和遍历一般树一样，可以使用广度优先（BFS, Breadth-First Search）或优先搜索（DFS, Depth-First Search）对图进行搜索遍历，BFS需要队列结构，而DFS则需要栈结构
  • 搜索过程中需要一个$\Theta(|V|)$空间的布尔数组或哈希表，以记录哪些顶点已经被搜索过
  • 搜索的最优时间复杂度为$O(|V|+|E|)$，最坏的情况则需$O(|V|^2)$复杂度

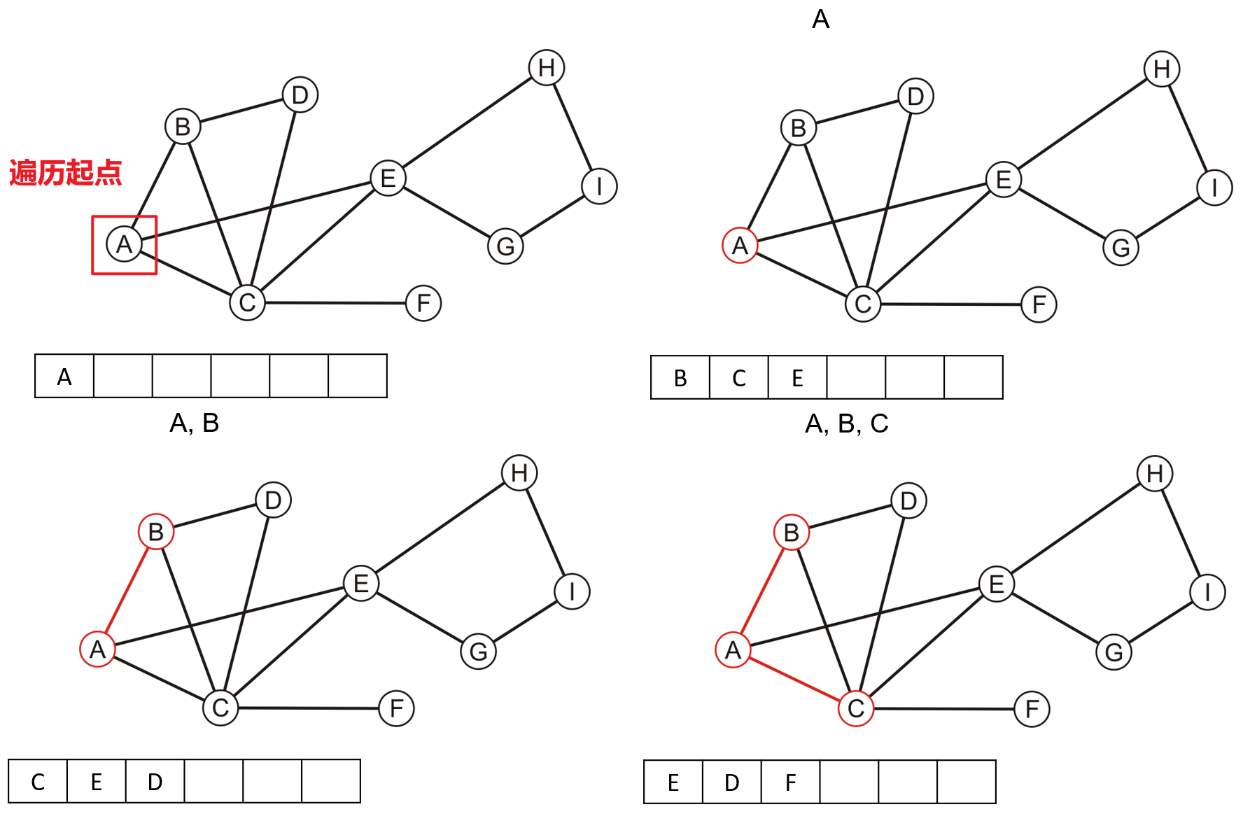
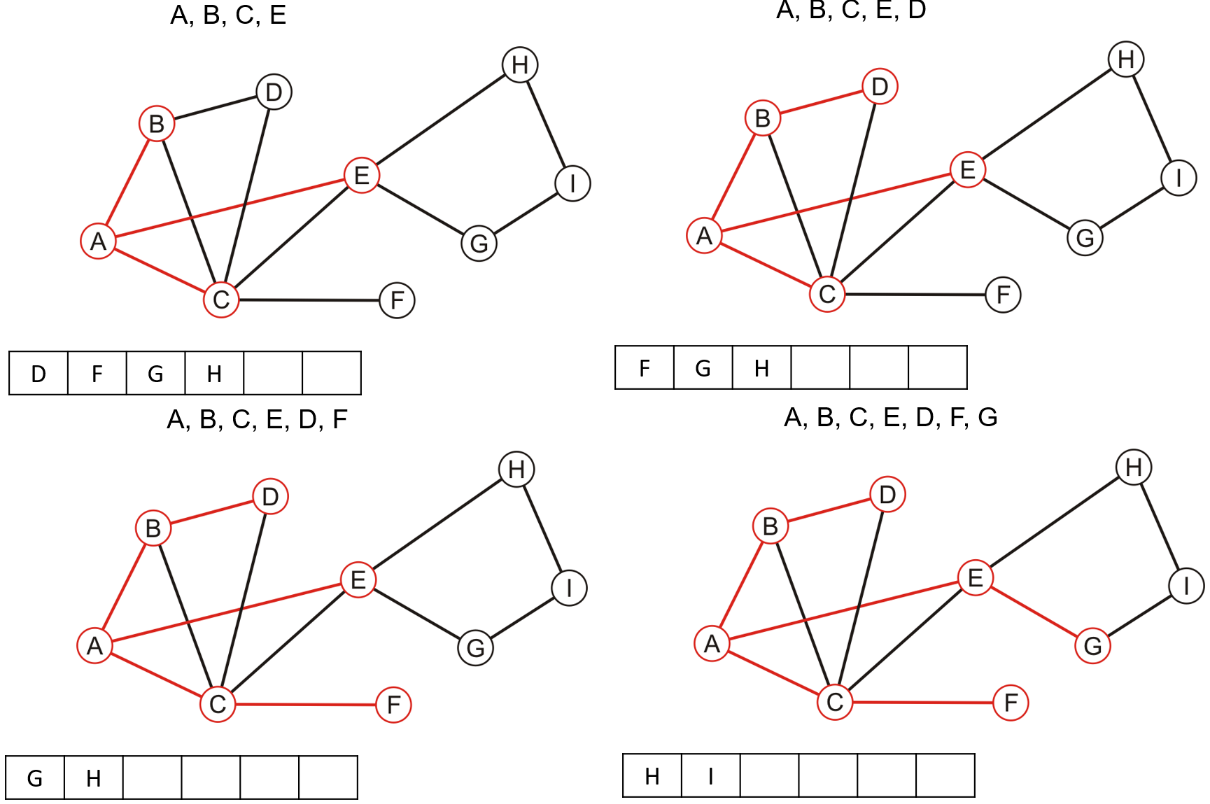
3.2 广度优先搜索

3.2.1 原理解析

• 首先选取任意一个顶点，在布尔数组中将其标记为已搜索过，并将其推送入BFS的队列中
  • 如果队列不为空，则取出队首顶点，将其所有的邻接顶点标记为已搜索，并推送到队列尾
  • 重复上述操作，直到队列为空
  • 若结束后布尔数组中的全部顶点均被标记为搜索过，则说明该图是连通的

3.2.2 代码实现

//Vertex是顶点的数据结构
void Graph::BFSTraversal(Vertex* _first) const
{
    //声明一个哈希表，存储已访问的顶点
    unordered_map<Vertex*, bool> _visited;
    _visited[_first] = true;

    //创建队列，初始化时将起始顶点加入队列
    std::queue<Vertex*> _queue;
    _queue.push(_first);

    //广度优先遍历
    while (!_queue.empty())
    {
        //取出队列中的第一个顶点
        Vertex* _v = _queue.front();
        _queue.pop();

		//实际应用场景中，此处可以对_v做某些检查操作来满足特定需求
		//...

        //遍历_v的所有相邻顶点
        for (Vertex* _i : _v->adjacentVertices())
        {
            //如果_i没有被访问过，则标记为访问过后将其加入队列
            if (_visited.find(_i) == _visited.end())
            {
                _visited[_i] = true;
                _queue.push(_i);
            }
        }
    }
}

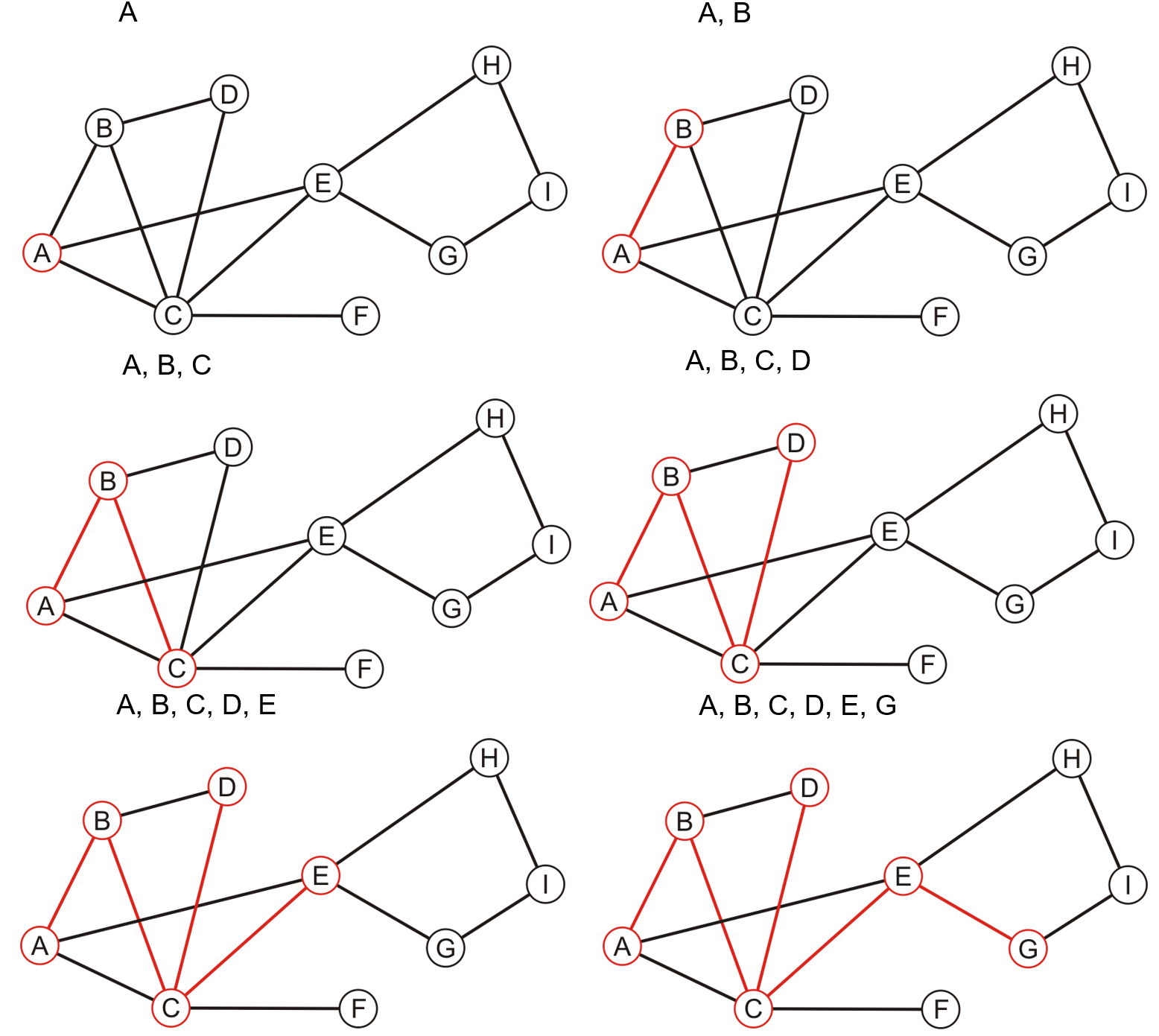
3.3 深度优先搜索

3.3.1 原理解析

• 首先任意选取一个顶点，标记其为已访问，然后从这个顶点开始
  • 依次遍历其邻接顶点，如果其有一个未被访问过的邻接顶点，则直接选中这个顶点继续搜索，这意味着可能前一个顶点的若干邻接顶点中可能有未被遍历到的
  • 如果选中的顶点的所有邻接顶点都已被访问过，则返回到最近被访问的某个顶点处，该顶点需要拥有未被检视过的邻接顶点，检视这些邻接顶点，若有未被访问的邻接顶点则选中之继续搜索，若无则继续回溯
  • 重复上述操作，直到没有任何一个已访问过的顶点拥有未被检视过的邻接顶点

• 对比BFS和BFS遍历，两种方法中所有顶点被遍历到的顺序不同

3.3.2 代码实现

• 以下是非递归版本的代码实现

void Graph::DFSTraversal(Vertex* _first) const
{
    unordered_map<Vertex *, bool> _visited;
    _visited[_first] = true;

    std::stack<Vertex *> _stack;
    _stack.push(_first);

    while (!_stack.empty())
    {
        Vertex *_v = _stack.top();
        _stack.pop();

		//实际应用场景中，此处可以对_v做某些检查操作来满足特定需求
		//...

        for (Vertex* _i : _v->adjacentVertices())
        {
            if (_visited.find(_i) == _visited.end())
            {
                _visited[_i] = true;
                _stack.push(_i);
            }
        }
    }
}

• 以下是递归版本的代码实现

//确立遍历的起点
void Graph::DFSTraversal(Vertex* _first) const
{
    std::unordered_map<Vertex *, bool> _visited;
    _visited[_first] = true;
    _first->DFSTraversal(_visited);
}

void Vertex::DFSTraversal(unordered_map<Vertex *, bool>& _visited) const
{
	//实际应用场景中，此处可以对该顶点做某些检查操作来满足特定需求
	//...

    for (Vertex* _v : this->adjacentVertices())
    {
        if (_visited.find(_v) == _visited.end())
        {
            _visited[_v] = true;
            _v->DFSTraversal(_visited);
        }
    }
}