浅析MSD与LSD优先的基数排序

一、原理解析

1.1 LSD基数排序介绍

• 设想我们要对在一定范围内的若干几十位的大数进行排序，我们仍然使用桶排序，会由于极差过大而导致所有桶开辟的总共$O(max-min+1)$的内存空间造成极大的浪费；对于这些大数，LSD基数排序（Radix Sort）的思路是：
  • 先统一所有数据的位数，即向位数最长的数对齐，缺位则在高位补$0$
  • 从最低位（如十进制的个位）开始，依照每位数字的大小对整个列表进行某种稳定的排序（一般使用桶排序中的计数排序），直到遍历完所有位，此时就完成了排序

• 若按照从第$1$位（最高位）数字到第$k$位（最低位）数字的顺序进行按位比较与排序，则该基数排序称为MSD（Most Significant Digit First）基数排序；反之则称为LSD（Least Significant Digit First）基数排序

1.2 LSD具体实现（十进制为例）

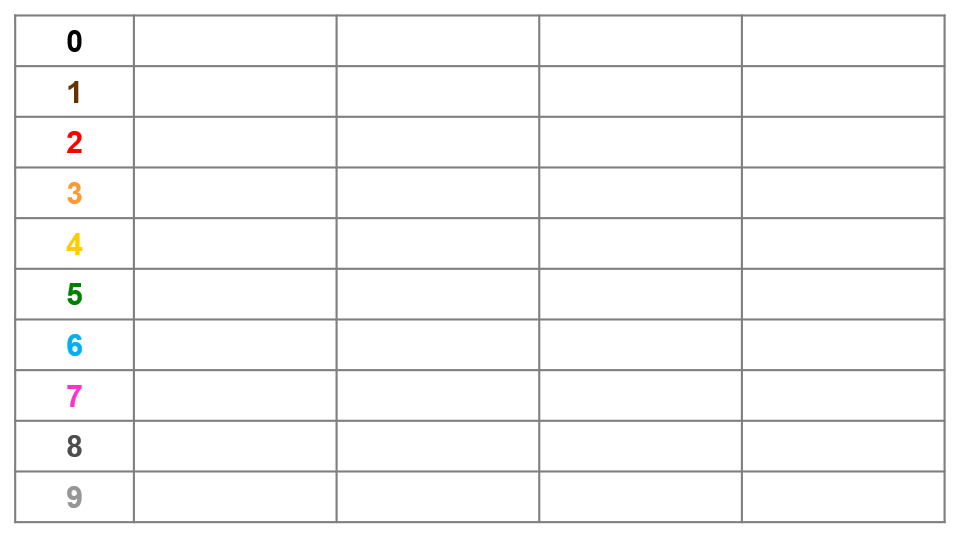
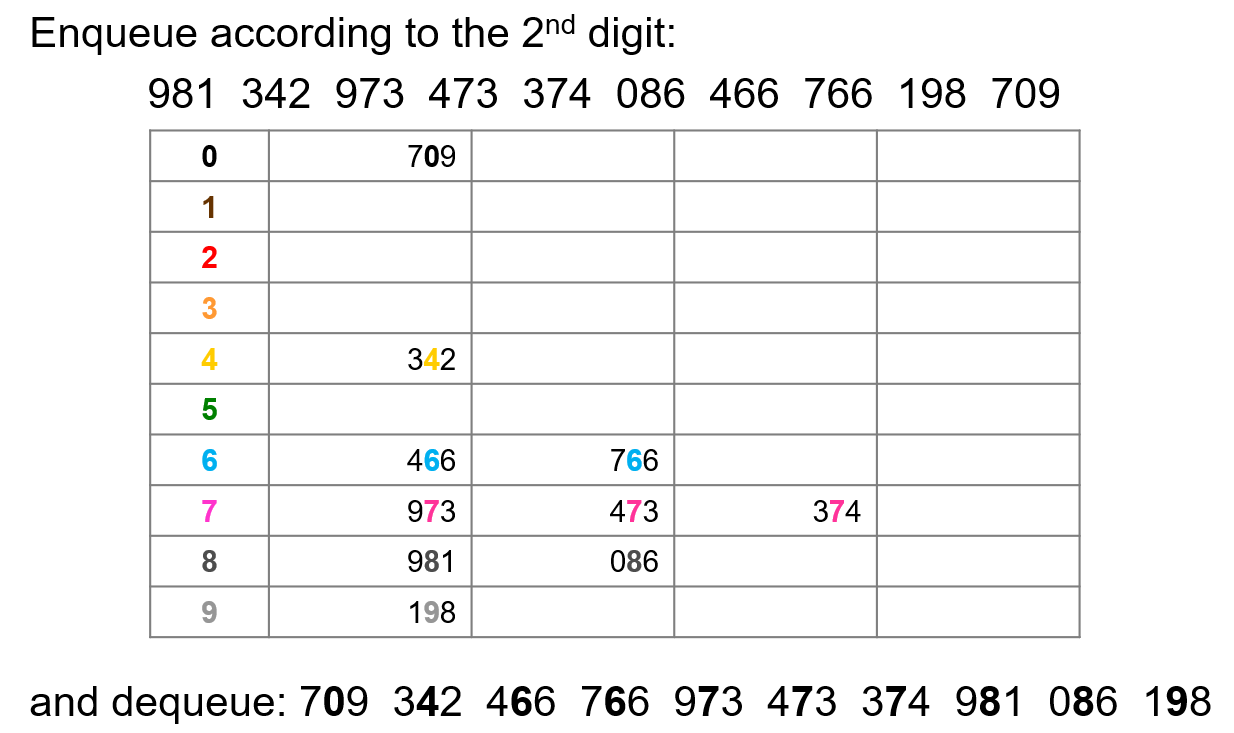
• 假设要对比$n$个位数为$m$的$k$进制数，我们就需要开辟$k$个队列（桶），我们先以十进制为例，此处相当于对每位数使用（基于链表而非计数器形式的）桶排序进行实现

• 从最低位（此处就是第3位）开始，按照该位的数字将其放入对应的桶（队列）中，然后再将桶中元素按序取出即可得到下一轮桶排序的输入

• 此轮对第$2$位数进行排序，将上一轮的位排序的结果作为此轮的输入，然后按序取出

• 重复上述操作直到最后一轮对最高位进行排序，此轮结束后按序取出的列表即为完成排序的列表

1.3 LSD具体实现（二进制为例）

• 对二进制进行基数排序（此处仍然是按位桶排序）同理，开辟两个队列

• 然后进行共五轮的入队、出队操作即可

1.4 LSD二进制实现的优化

下面这种方法只使用到了一个列表，相比十进制的需要维护十个队列的实现更加简单，所以我们也可以将十进制（或其它进制）数化为二进制数后使用下面的方法进行基数排序，这样只需要实现一个基数排序而应用到所有进制的数的排序上

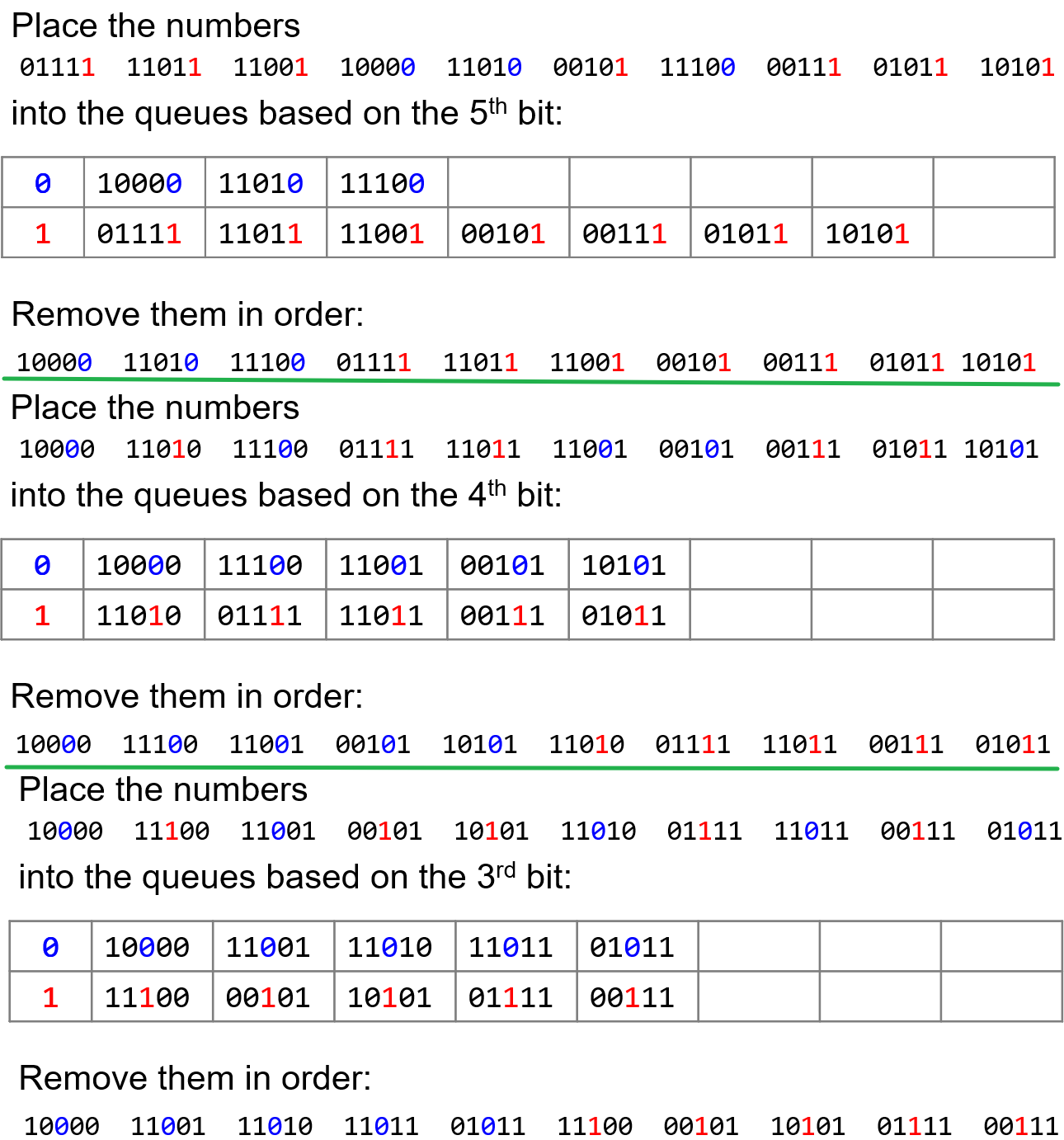
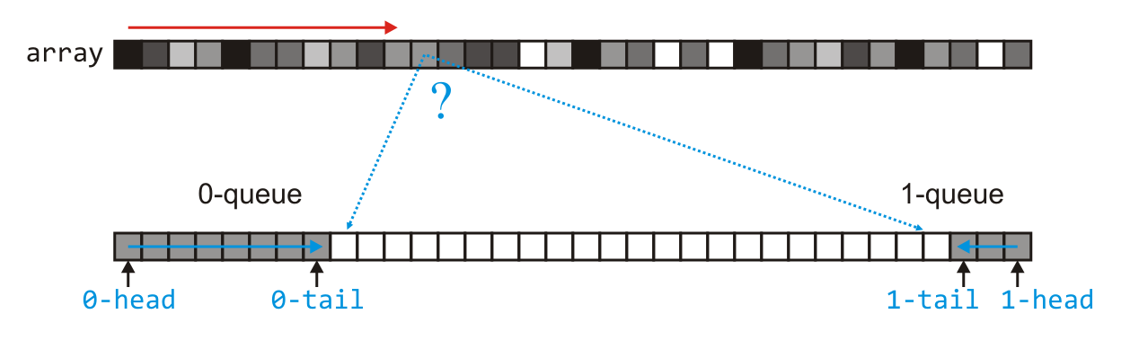
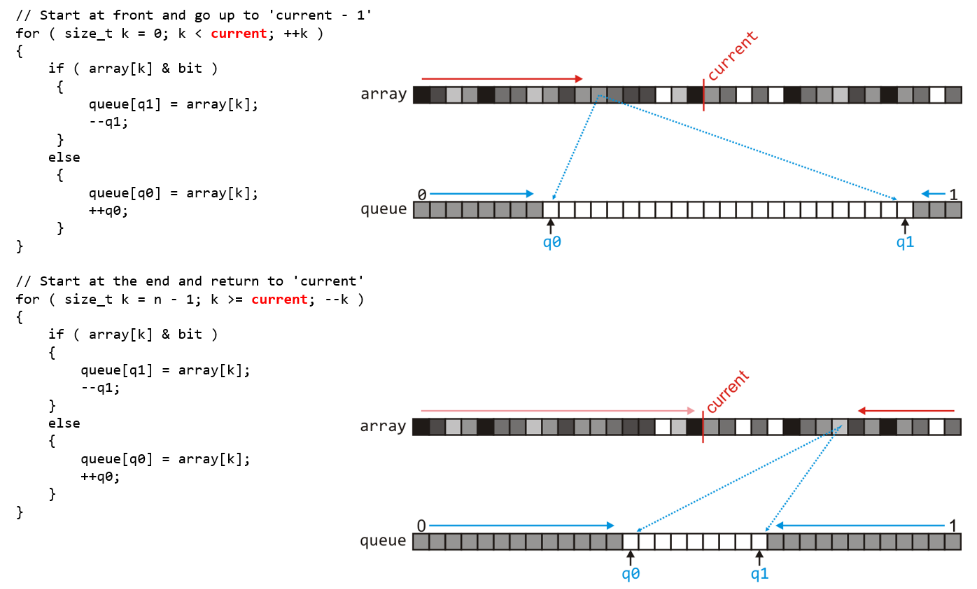
• 上述的$k$个队列的实现方法中，我们可以看到这$k$个队列中的总元素数量始终为$n$个，所以对于二进制的数我们可以只使用一个固定长度$n$的列表，按位桶排序的时候将该列表的两端当作$0$和$1$的桶来推送元素

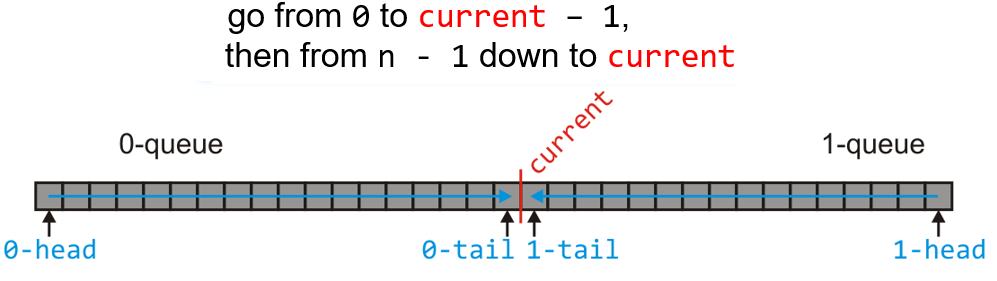
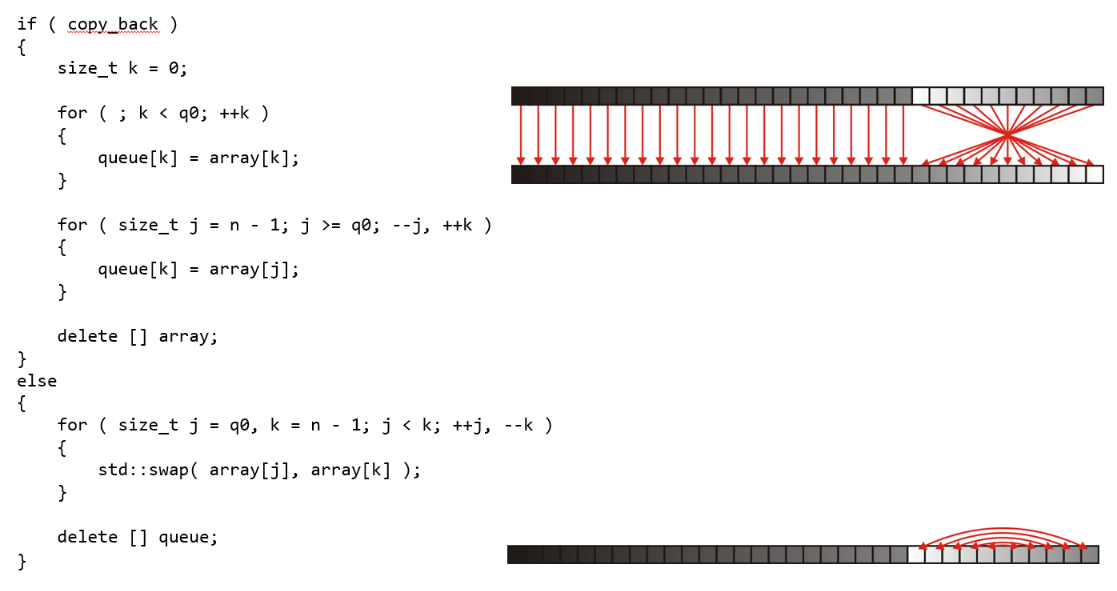
• 上图这样每次按位插入完所有待排序元素后，由于左半部分（0桶）从是从小到大排列的，右半部分（1桶）是从大到小排列的，所以我们在取出元素的时候需要以正确的顺序取出（在取出时我们就可以）

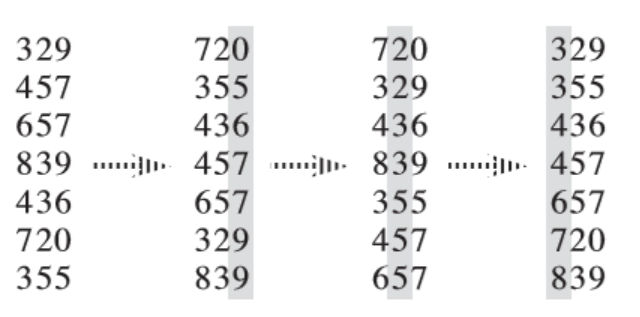
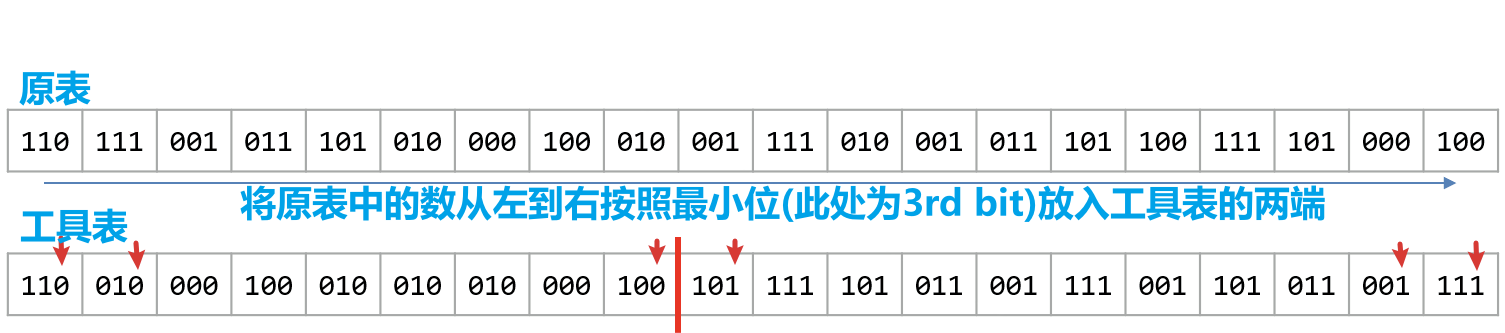
• 我们以下图的这20个十进制数的排序为例

• 然后按照上面的规则按位进行放入，下图是对3rd位的排序，将原列表的数全部按规则放入工具表中后，原列表中的数已经全部没有意义了，故而可以被当作下一轮排序的放置容器

• 进行第二轮按位排序，此处是对2nd位的排序

• 然后依此类推进行1st位的排序，完成后只需将工具表中的元素按照大小顺序取出即可

• 然后将二进制转换为十进制即可

1.5 MSD基数排序介绍

• 不同于LSD从最低位开始逐位比较，MSD基数排序的思路是：
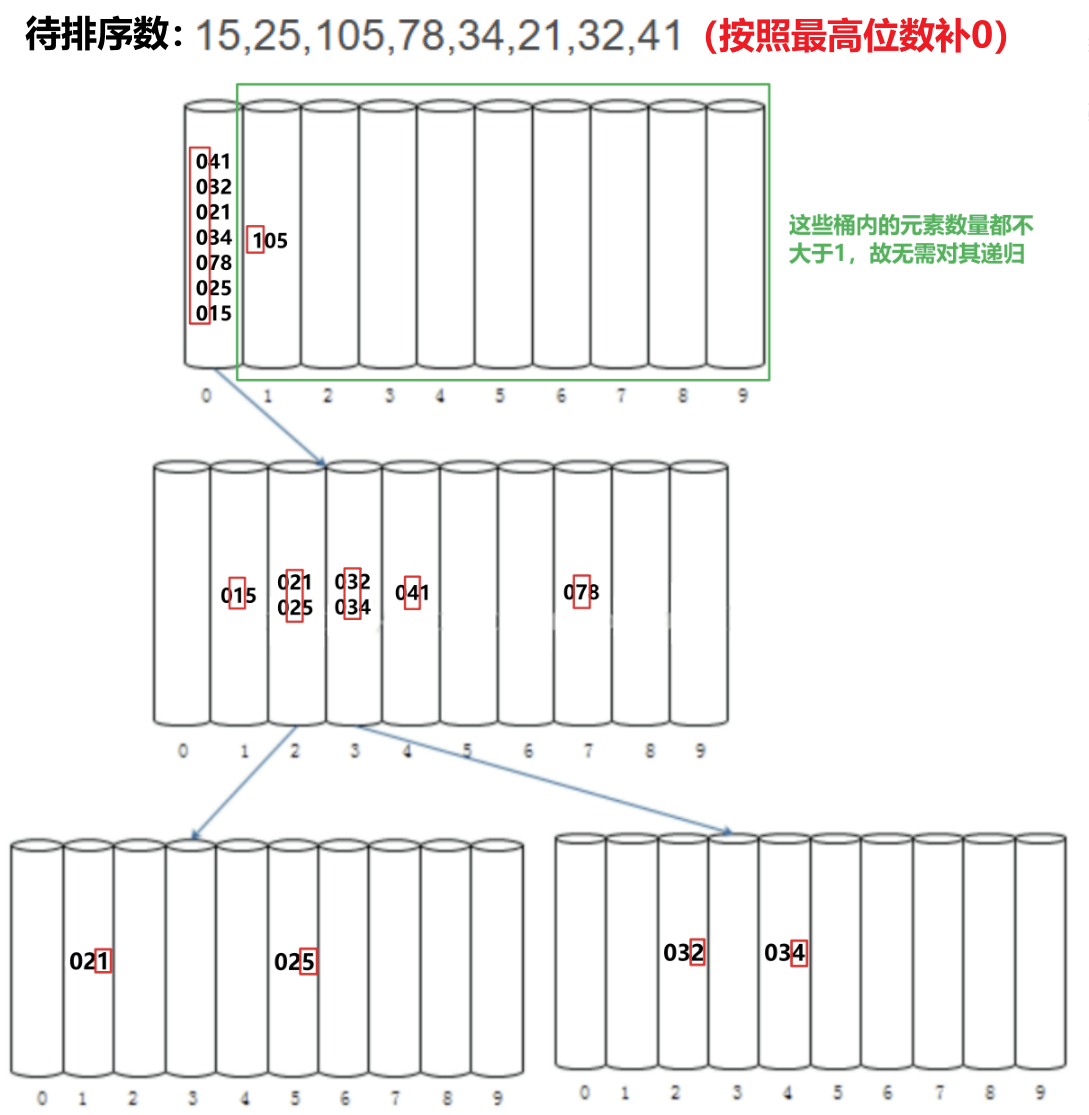
  • 先将所有的数据按照最高位放入桶中（以十进制数为例，有十个桶），然后对每个桶内元素数量进行检测，数量大于$1$的桶需要被递归地从次高位开始调用MSD基数排序
  • 递归到最低位完成后，将排好序的元素按序塞回上一层递归的桶内，直到返回最外层（依据最高位大小入桶的那层）的对应桶中，则该桶便完成了排序
  • 直到最外层所有桶都递归地排完序，再从其中将元素按序取出，MSD基数排序就完成了

• 这种方式下由于是从最高位开始，在此过程中只要同位上的数大小有差异，那么数据的大小便已经分出来了（放在桶中而无需再动，如上图递归第一层的105、第二层的078等），所以每层桶进入下一层递归时只需对仍未分出大小的那些数据（即数据量大于$1$的桶中的数据）按照次高位大小进行再排序即可

二、复杂度分析

2.1 LSD的时间复杂度

• 对总共$n$个位数为$m$的$k$进制数进行LSD基数排序，如果按照每位数字的基数$k$（如十进制数的每位数字取值范围最大是$[0,9]$）开辟$k$个桶进行桶排序，最开始的建桶需要$O(k)$的复杂度
• 每轮排序中，遍历所有$n$个数据分配到对应桶中需要$O(n)$的时间复杂度，将各桶中的元素按序取出的时候就无需逐一取出，而是将各桶首位相连即可，需要$O(k)$的复杂度，故单轮排序共需

\[O(n+k)\]

• 总共需要进行$m$轮的上述排序操作，如果我们最开始建的桶可以复用，则总共的时间复杂度为

\[O(k+m(n+k))=O(mn+(m+1)k)\]

• 实际情况中，需要被排序的数据的数量$n$通常是远大于数据本身的进制$k$的，而数据的位数$m$就是一个常数而已，所以上述复杂度在这种情况下就近似为

\[O(n)\]

• 若想减小LSD的空间复杂度，则需要尝试减少桶数，而由于$k$进制数的每位数字并不一定需要$k$个桶（如对十进制的$13,11,21,44$这四个数的个位数进行计数排序，只需$3$个桶即可，若也$10$个桶会造成空间的浪费），为此我们需要对每位数字进行严格的计数排序
• 这样的话每轮都需要动态地建$k_i$个桶（$i$代表轮数），每轮需要的时间复杂度就为

\[O(k_i)_{建桶}+O(n)_{分配数据入桶}+O(k_i)_{合并桶中元素}=O(n+2k_i)\]

• 同样需要进行$m$轮，总时间复杂度就为

\[O(mn+2\sum_{i=1}^m{k_i})\]

• 在$n»k_i$条件下我们同样可以得到近似的$O(n)$的时间效率

2.2 MSD的时间复杂度

• MSD基数排序是递归的实现思路，在理想情况下（被排序数的相似率很高，仅有若干位数字存在不同）是十分快速的，并且在数位$m$很多的情况下在时间效率上一般是优于LSD的（LSD无论位数多少都要从最低位开始遍历完$m$轮，而MSD可能递归个几轮就完事儿了）
• 由于实际情况复杂多变，MSD产生的递归子问题的规模难以衡量，所以MSD的时间复杂度的大小是需要依据被排序数据的性质来具体分析的，在此处我没办法给出很General的分析

三、代码实现

• 由于有点忙，暂时懒得自己写，后面有空补上