浅析桶排序与计数排序

一、原理解析

1.1 计数排序

计数排序是一种特殊的桶排序，当桶的数量取最大的$(max-min+1)$时就变成了计数排序

• 计数排序针对一组特定范围内的数，使用该组元素的极差$+1$的大小（$\geq$该组元素的个数$n$）开辟一个对应长度的布尔值表，然后将该组元素依次放入与表索引下标相等的位置，全部放入后就完成了排序，我们只需取出该表中值为1的项的索引，就得到了一个有序的列表

• 当需要被排序的那组数中有重复的项（哈希表中发生冲突/碰撞）时，我们可以用链表（把重复的对象链在哈希表中的同一位置）或者计数器的方式（表的元素不再使用bool而是使用无符号整数来记录该位置上对应大小的项出现的次数）来解决
  • 链表的方式：适用于某些对象在需要被排序的属性上相同，但在其它属性上仍有差异，不能单纯使用数量的累加来解决的场景下
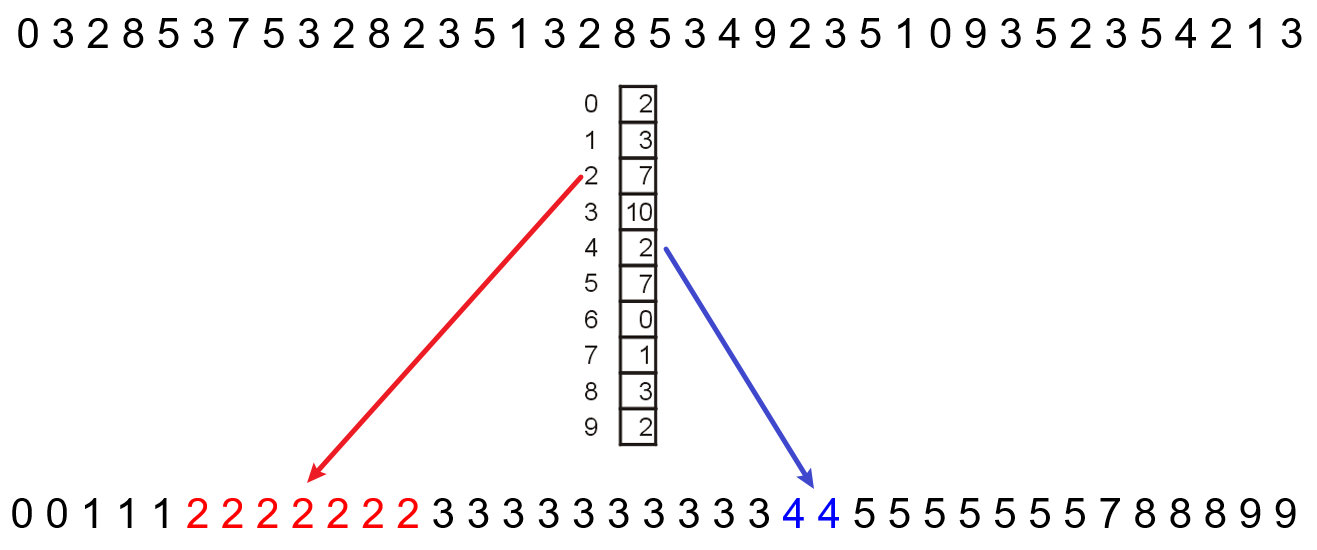
  • 计数器的方式：适用于多个对象完全相等而可以被累加的情况下，如下图所示

• 上述例子中的被排序数都是从0开始的，若不从0开始，使用同一个索引从0开始的表时，就需要在放入和取出的时候考虑一个偏移量min（被排序的那组数中的最小值），如下例所示
  • nums=[1,6,7,1,5]，先遍历列表获取最小值min=1和最大值max=7，开辟一个长度为7-1+1=7的计数器数组counter，统计每个元素出现的频率得counter=[2,0,0,0,1,1,1]
  • 收集：counter[0]=2表示0+min=1出现了2次，向nums覆写入2个1，counter[1]=0表示1+min=2出现0次，无需覆写，依次类推得到nums=[1,1,5,6,7]，排序完成

1.2 桶排序思路

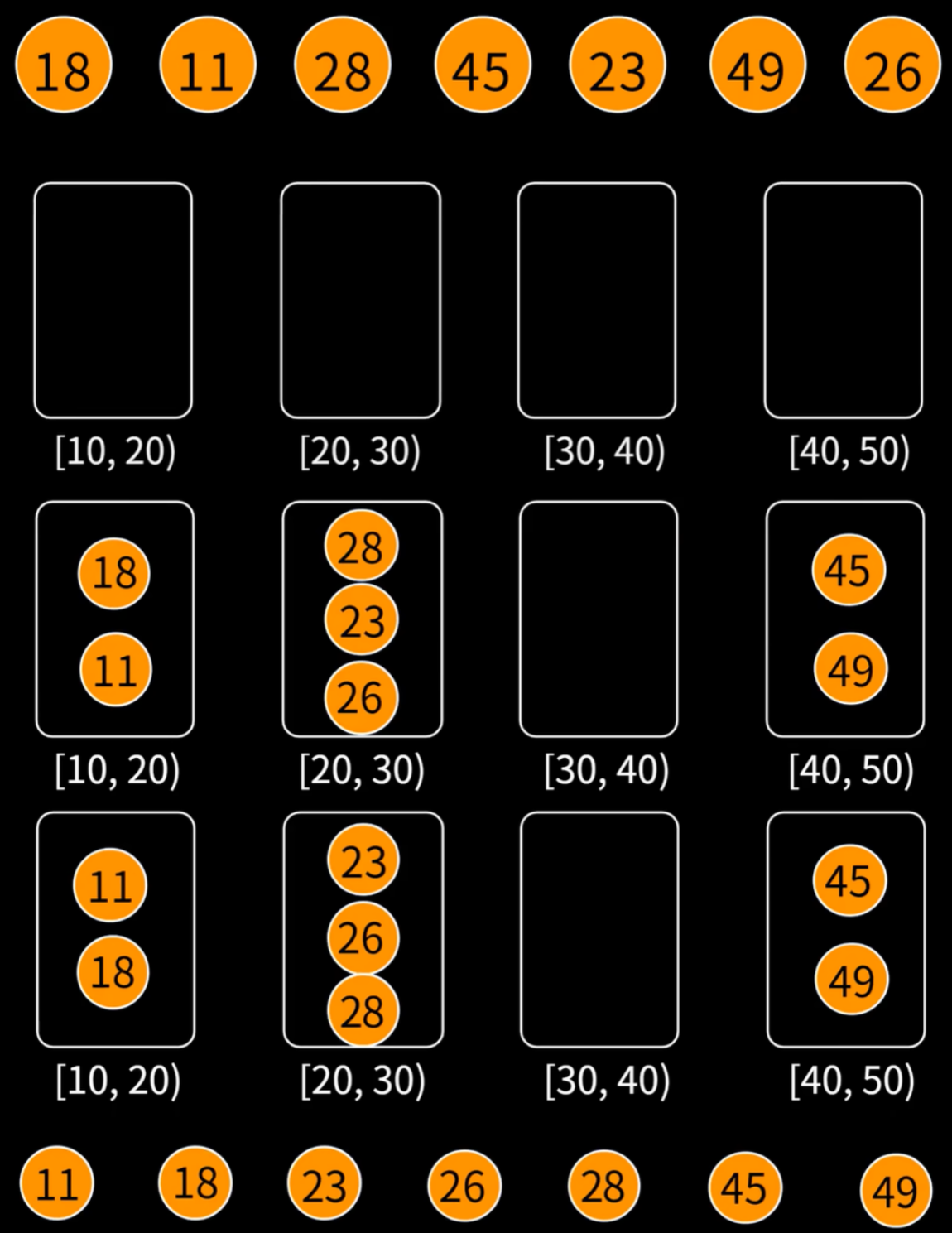
• 我们将要排序的一组$n$个数按照取值范围，设置最多$(max-min+1)\geq n$个桶（一般设置$n$个桶来最大化时间效率，详见复杂度分析）来装填对应范围内的数，将所有数填入后再分别将非空桶内排序（可以按照对时间或空间效率等需求来选择快速排序或插入排序等），然后把非空桶合并成整体即完成排序

二、复杂度分析

桶排序的高时间效率建立在”被排序的数是均匀分布在一定范围内（且范围可以很大，但数据一定要较为均匀地分布）”的前提假设之上

2.1 时间复杂度

• 假设被排序的数据是均匀分布的，我们采用$k$个桶，则每个桶的元素平均个数为$\frac{n}{k}$，假设选择用快速排序对每个桶内元素进行排序，那么每次排序的时间复杂度为$O(\frac{n}{k}\ln\frac{n}{k})$，总时间复杂度如下所示（遍历$n$个数据并放入桶中+对$k$个桶分别进行快速排序+将$k$个桶内的元素进行合并）

\[O(n)+k\cdot O(\frac{n}{k}\ln\frac{n}{k})+O(k) = O(n+n\ln\frac{n}{k}+k)\]

• 若在相同条件下使用插入排序，则时间复杂度为

\[O(n)+k\cdot O(\frac{n^2}{k^2})+O(k) = O(n+\frac{n^2}{k}+k)\]

• 当$k$接近于$n$时，桶排序的时间复杂度就近似是$O(n)$
  • 这个结论建立在我们能使用$\frac{n}{k}$来表示每个桶内的数据数量的前提上，即数据分布要均匀
  • 在此基础上$k\approx n$也即每个数据都能落在一个桶的范围内，若不均匀则会出现若干空桶
  • 数据分布的范围$(max-min+1)$可以很大，这不会影响效率，但一定要有范围才行

2.2 空间复杂度

• 所有桶所需占用的总空间为数据总数$n$，故空间复杂度为$O(n)$

三、代码实现

//待完成