浅析并查集的实现与应用

一、关于并查集

1.1 不相交集合

• 回忆离散数学中的关系（Relation）章节中的等价关系（Equivalence Relation）相关概念
  • 等价关系即同时满足自反性、对称性、传递性的关系
  • 一个等价关系会将一个集合$A$分区为多个互不相交的等价类（Equivalence Class）
  • 等价类内的元素称为该等价类的代表（Representative），它们互为等价元素
• 这些等价类由于其不相交性，也被称为不相交集合（Disjoint Set），而被分区为若干个不相交集合的集合$A$被称为并查集（DSU, Disjoint Set Union）

1.2 并查集操作

• 关于并查集，我们常需要对其做以下两种操作
  • Find：查询$A$的并查集中的某个元素属于哪个不相交集合
  • Union：合并两个不相交集合集为一个新的集合

二、并查集的实现

2.1 逻辑上以树结构理解

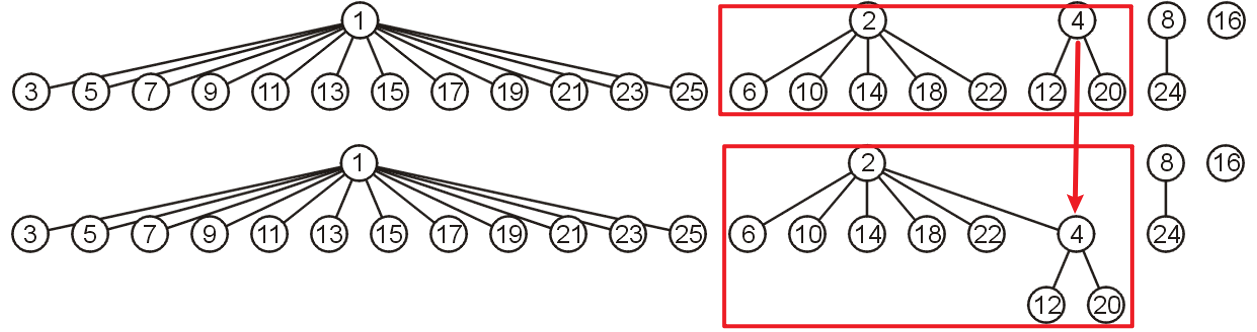
• 通常我们会采用一系列一般树来实现并查集，如下图所示是某个集合$A$中的所有不相交集合树
  • 这种实现方法中，集合$A$中的元素以节点的形式存在
  • 每个树的所有节点都同属一个不相交集合，根节点可以是其中的任意代表

• 暂不讨论其Find操作，其Union操作需将其中一棵树的根节点附加到另一棵树的根节点上

2.2 代码中借助数组实现

2.2.1 实现思路

除了下面的方法外，也可以将根节点对应在数组arr中的元素维护为一个负数，其绝对值表示其所在不相交集合的元素数，而非根节点对应arr中的元素值则使用正数，作为索引指向其父节点

• 我们声明一个长度和元素总数$n$相等的数组arr（虽然实际存储并查集结构的是数组，但我们可以通过上文讲到的树的结构来进行理解）
  • 如果索引i处的元素值等于i的话（即arr[i] == i）则说明该索引处的元素节点是树的根节点，该实现下的并查集中的不相交集合的个数，就等于数组中的arr[i] == i的根节点元素个数，每个根节点唯一确定一个不相交集合
  • 如果arr[i] != i，则arr[i]表示该节点的父节点的索引值，父节点不一定是根节点

2.2.2 查找操作

• 其Find操作的实现如下，时间复杂度等于$O(h)$，其中$h$指的是树高

//非递归写法
size_t DisjointSetUnion::Find(size_t _idx) const
{
	//从数组的_idx处的节点不断向上回溯其父节点，知道回溯到根节点
	while(arr[_idx] != _idx)
	{
		_idx = arr[_idx];
	}
	//返回找到的根节点的索引，这样我们就算是找到了传入节点所处的等价类了
	return _idx;
}

//递归写法（函数调用堆栈使用额外O(h)的空间复杂度）
size_t DisjointSetUnion::Find(size_t _idx) const
{
	return arr[x] == x ? x : Find(arr[x]);
}

2.2.3 合并操作

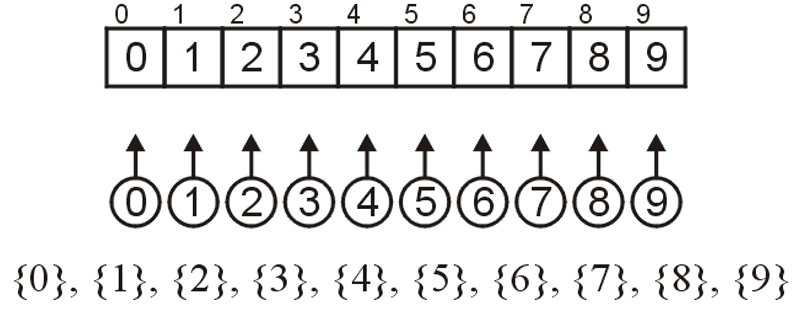
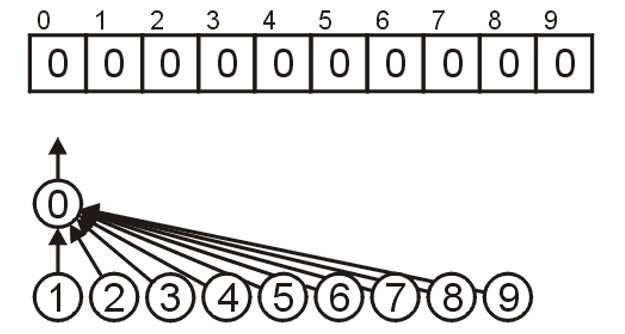
• 我们将数组初始化为离散的$n$个元素（即$n$个不相交集合），如下图所示

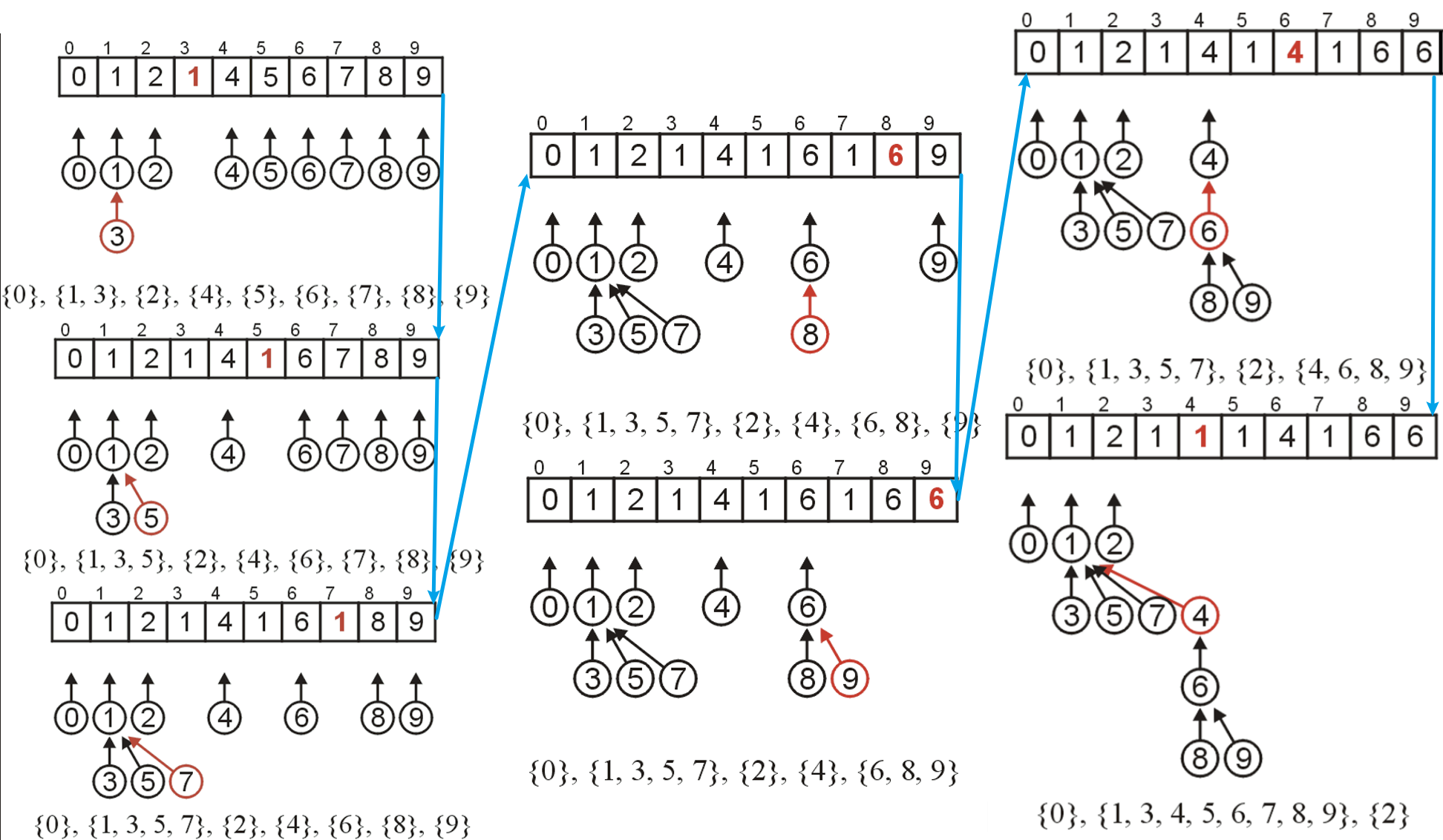
• 然后我们若想将合并两个集合，则需知道这两个集合的根节点在数组中的索引，比如i和j，如果想将前者对应集合合并到后者集合内，则我们只需要将arr[i]的值改为j即可，这 样i节点下的所有子节点在使用Find回溯根节点时就会回溯到j处，这样就完成了合并

• 合并的代码实现如下所示，该函数接收两个索引参数，为了提高鲁棒性我们需要确保二者均为根节点索引，所以时间复杂度为$2\cdot O(h) + O(1) = O(h)$

void DisjointSetUnion::Union(size_t _idx1, size_t _idx2)
{
	//确保两个索引处的元素是根节点
	_idx1 = Find[_idx1];
	_idx2 = Find[_idx2];
	//将_idx1所属集合合并到_idx2所属集合上
	if (_idx1 != _idx2)
		arr[_idx1] = _idx2;
}

2.3 优化时间复杂度

2.3.1 矮树接高树

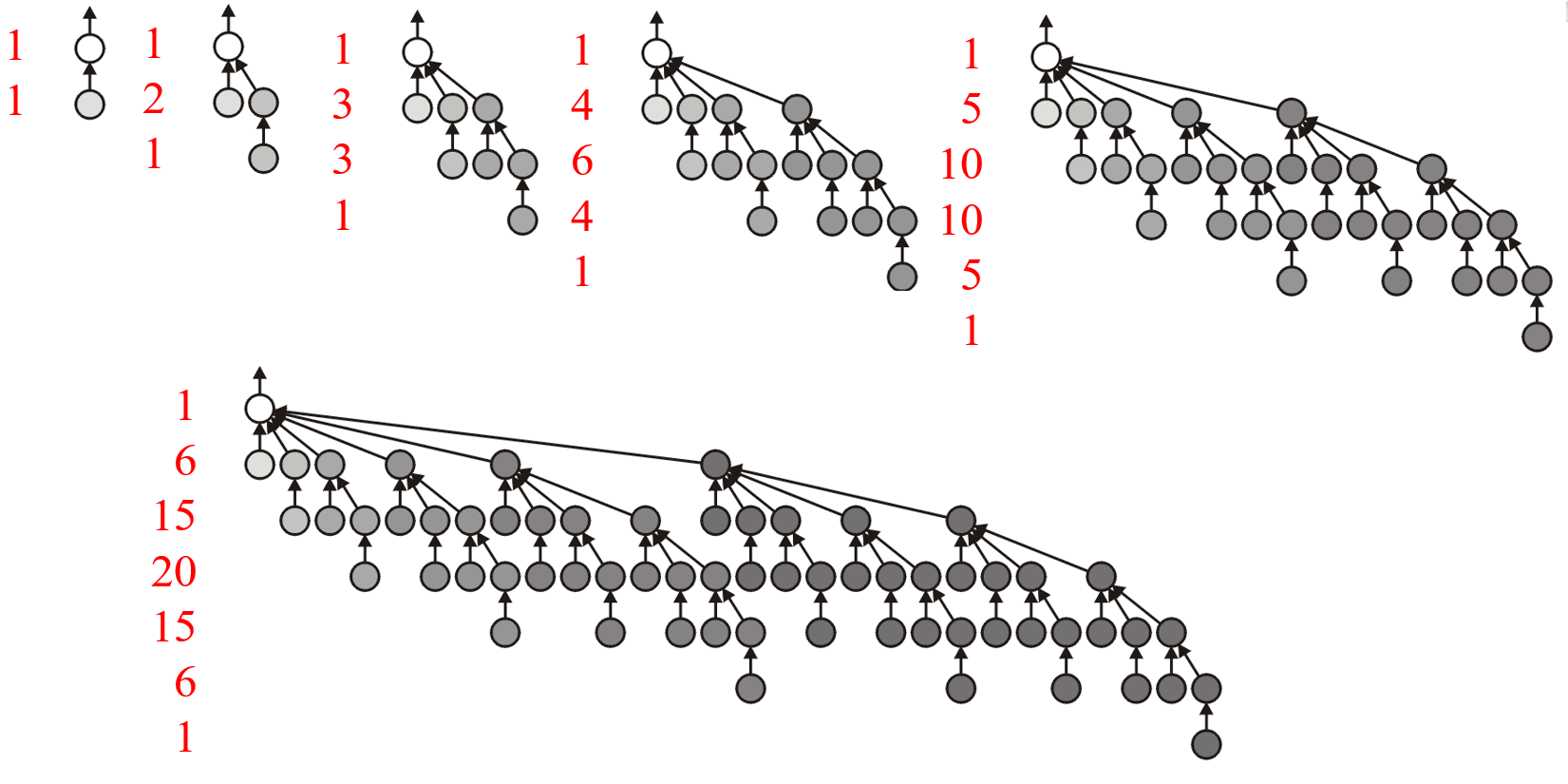
• 我们从代码实现中可以看出，为了使得Find和Union时间复杂度最小，则需降低树高h，其中一种思路是将树高较小的树合并到较高树的根节点上
• 该方法最坏情况就是每次合并两个树的高度都相同，这样合并后的树高总会比原先的增高$1$个节点，下图的红色数字表示对应深度的节点数，由此可计算出最坏情况的节点的平均深度为$O(\ln{n})$

• 最好情况则是如下图，其节点平均深度为$O(1)$

• 平均情况较为复杂，参考此处的解析，平均深度为$\Theta(1)$

2.3.2 路径压缩

• 可以对Find函数进行路径压缩优化，使得每次调用Find(_i)时，都将_i对应节点（及其与根节点之间路径上的所有节点全部都）改接到其所在不相交集合的根节点上，以确保并查集中的所有树高度维持在$1$
• 我们也可以在每次调用Union时就将路径压缩，但是Union函数本身就是要调用Find函数的，所以二者并无根本上的区别
• 下面是递归的实现方法，使得下一次Find(_i)时的时间复杂度降为$O(1)$，但是需要耗费$O(h)$的空间复杂度，因为递归算法会使用函数调用堆栈从而造成空间的开销

//递归的路径压缩优化Find函数
size_t DisjointSetUnion::Find(size_t _i)
{
	if (arr[_i] == _i)
		return _i;
	else
	{
		//将_i向上寻根的路径上全部的节点都接到根节点上
		arr[_i] = Find(arr[_i])
		return arr[_i];
	}
}

• 当然也可以使用非递归的方式实现，如下所示

size_t DisjointSetUnion::Find(size_t _i)
{
	//先找到根节点索引
    size_t _root = _i;
    while (arr[_root] != _root)
        _root = arr[_root];
	//将路径上所有节点改接到根节点上
    while(_i != _root)
    {
        size_t _temp = arr[_i];
        arr[_i] = _root;
        _i = _temp;
    }
    return _root;
}

三、并查集的应用

• 此课件内介绍了DSU被用于图像处理、迷宫生成的两个例子