浅析并查集的实现与优化方法

一、关于并查集

1.1 不相交集合

• 回忆离散数学中的关系（Relation）章节中的等价关系（Equivalence Relation）相关概念
  • 等价关系即同时满足自反性、对称性、传递性的关系
  • 一个等价关系会将一个集合$A$分区为多个互不相交的等价类（Equivalence Class）
  • 等价类内的元素称为该等价类的代表（Representative），它们互为等价元素
• 这些等价类由于其不相交性，也被称为不相交集合（Disjoint Set），而被分区为若干个不相交集合的集合$A$被称为并查集（DSU, Disjoint Set Union）

1.2 并查集操作

• 关于并查集，我们常需要对其做以下两种操作
  • Find：查询$A$的并查集中的某个元素属于哪个不相交集合
  • Union：合并两个不相交集合集为一个新的集合

1.3 并查集应用

• 此课件内介绍了DSU用于图像处理、迷宫生成的示例，建议先看完后文原理再回来阅读，然后可尝试用并查集解决力扣上的岛屿数量问题（下方给出题解，其中并查集的实现参考后文）

class DisjointSetUnion
{
private:
    //对于元素值等于索引值的元素，其为所在不相交集合的根节点
    //对于元素值等于索引值的元素，其元素值是其父节点的索引值
    std::vector<size_t> parent;

    //用于按秩合并优化，合并时将矮树挂到高树下以降低树的高度
    //只有当某节点为根节点时，其秩值才有意义，用于衡量其树高度
    std::vector<size_t> rank;

    //缓存不相交集合的数量
    size_t setNum;

public:
    DisjointSetUnion(size_t);        //并查集中元素的个数
    
    size_t Find(size_t);             //查询某个元素所处不相交集合的根节点
    void Union(size_t, size_t);      //合并两个不相交集合集为一个新的集合

    size_t GetSetNum() const;        //获取并查集中不相交集合的数量
};

DisjointSetUnion::DisjointSetUnion(size_t _size)
{
    //每个元素初始时都作为一个独立的不相交集合
    parent.resize(_size);
    for (size_t i = 0; i < _size; i++)
        parent[i] = i;

    //不相交集合数量
    setNum = _size;

    //所有的秩初始为0
    rank.resize(_size, 0);
}

size_t DisjointSetUnion::Find(size_t _idx)
{
    //迭代法，先获取根节点索引
    size_t _root = _idx;
    while (_root != parent[_root])
        _root = parent[_root];
    //然后再压缩路径
    while (_idx != _root)
    {
        size_t _backup = parent[_idx];
        parent[_idx] = _root;
        _idx = _backup;
    }
    //最后返回根节点索引
    return _root;
}

void DisjointSetUnion::Union(size_t _idx1, size_t _idx2)
{
    _idx1 = Find(_idx1);
    _idx2 = Find(_idx2);
    //若归属集合相同，则无需进行后续检查
    if (_idx1 == _idx2) return;
    
    //按秩合并决策树，若树1较矮则挂到树2，若树2较矮则挂到树1
    if (rank[_idx1] < rank[_idx2])
        parent[_idx1] = _idx2;
    else if(rank[_idx1] > rank[_idx2])
        parent[_idx2] = _idx1;
    else
    {
        //秩相等时任意挂接
        parent[_idx2] = _idx1;
        //被挂载根节点对应的秩值递增
        rank[_idx1]++;
    }

    //不相交集合数量递减
    setNum--;
}

size_t DisjointSetUnion::GetSetNum() const
{
    // size_t _num = 0;
    // for (size_t i = 0; i < parent.size(); i++)
    // {
    //     if (i == parent[i])
    //         _num++;
    // }
    // return _num;

    return setNum;
}

class Solution
{
public:
    int numIslands(vector<vector<char>>& grid)
    {
        size_t rowNum = grid.size();
        size_t colNum = grid[0].size();
        
        //初始化并查集，最终会将所有0放到一个集合，其余各岛屿分别为一个集合
        DisjointSetUnion dsu(rowNum * colNum);
        
        //记录上一个水格子的dsu索引
        int dsuIdxWater = -1;
        //逐行遍历
        for (size_t y = 0; y < rowNum; y++)
        {
            //逐列遍历
            for (size_t x = 0; x < colNum; x++)
            {
                //计算当前格子对应并查集dsu中的索引
                size_t dsuIdx = y * colNum + x;
                
                //遇到水格子就将其统一合并
                if (grid[y][x] == '0')
                {
                    if (dsuIdxWater == -1)
                        dsuIdxWater = dsuIdx;
                    else
                        dsu.Union(dsuIdxWater, dsuIdx);
                }
                //否则进行岛屿合并判断
                else
                {                    
                    //若上方存在毗邻岛屿，则将当前格所代表的不相交集合和毗邻岛屿进行合并
                    //注意由于y和x是size_t，要避免出现类似(y-1>=0)这种东西，会越界UB
                    if (y >= 1 && grid[y - 1][x] == '1')
                        dsu.Union(dsuIdx, (y - 1) * colNum + x);
                    //上方和左侧都得并入，因为当前节点可能作为连接上方岛屿和左侧岛屿的桥梁
                    if (x >= 1 && grid[y][x - 1] == '1')
                        dsu.Union(dsuIdx, y * colNum + (x - 1));
                }
            }
        }
        //若存在水域，则除去水域代表的集合剩下的就是岛屿数量；否则不存在水域则直接返回
        return (dsuIdxWater != -1) ? dsu.GetSetNum() - 1 : dsu.GetSetNum();
    }
};

二、并查集实现

2.1 逻辑上以树结构理解

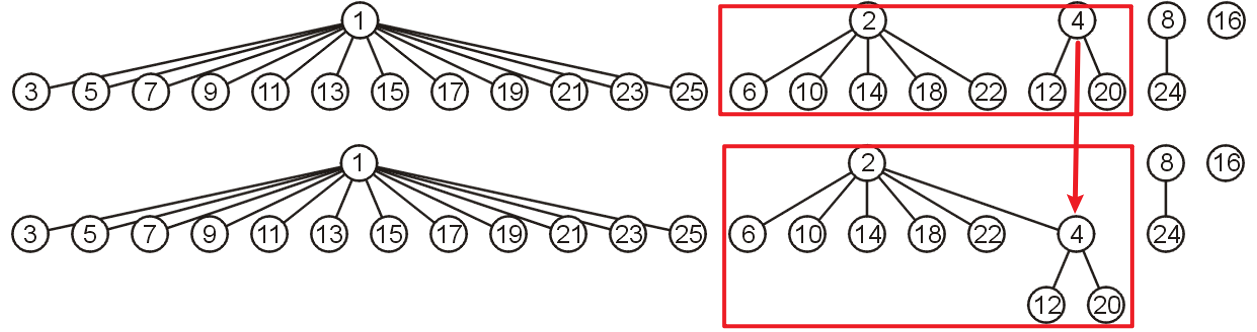
• 通常我们会采用一系列一般树来实现并查集，如下图所示是某个集合$A$中的所有不相交集合树
  • 这种实现方法中，集合$A$中的元素以节点的形式存在
  • 每个树的所有节点都同属一个不相交集合，根节点可以是其中的任意代表

• 暂不讨论其Find操作，其Union操作需将其中一棵树的根节点附加到另一棵树的根节点上

2.2 代码上借助数组实现

除了下文中的方法（根节点的索引值等于元素值）外，也可将根节点对应在数组parent中的元素维护为一个负数，其绝对值表示其所在不相交集合的元素数，非根节点对应parent中的元素值则使用非负数作为索引指向其父节点

2.2.1 实现思路

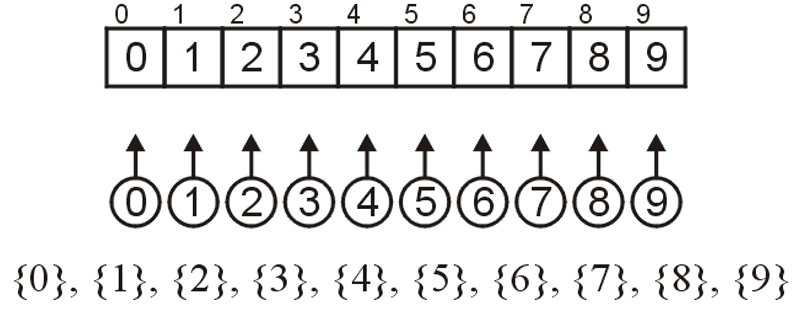
• 声明一个长度和元素总数$n$相等的数组parent（虽然实际存储并查集结构的是数组，但我们可以通过上文讲到的树的结构来进行理解）
  • 若索引idx处元素值parent[idx] == idx，则说明该索引处元素是树根节点，由于每个根节点唯一确定一个不相交集合
  • 若parent[i] != idx，则parent[idx]表示该节点的父节点的索引值，父节点不一定是根节点
• 该实现下，并查集中不相交集合的个数等于数组中parent[idx] == idx的元素数

2.2.2 查找操作

• 其Find操作的实现如下，时间复杂度等于$O(h)$，其中$h$指的是树高

size_t DisjointSetUnion::Find(size_t _idx) const
{
    //递归写法，函数调用堆栈使用额外O(h)的空间复杂度
    // return parent[x] == x ? x : Find(parent[x]);

    //迭代写法，从数组的_idx处的节点不断向上回溯其父节点，知道回溯到根节点
    while(parent[_idx] != _idx)
        _idx = parent[_idx];
    //返回找到的根节点的索引，这样我们就算是找到了传入节点所处的等价类了
    return _idx;
}

2.2.3 合并操作

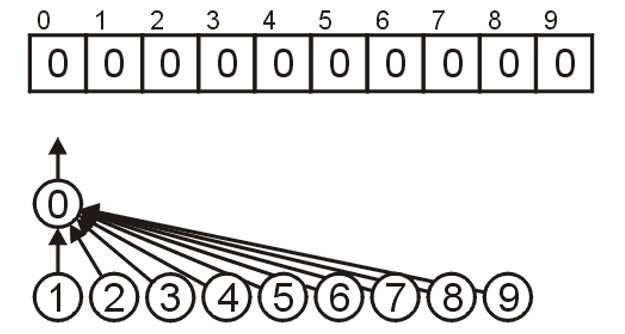
• 将数组初始化为如下图所示的$n$个离散的元素，即$n$个不相交集合

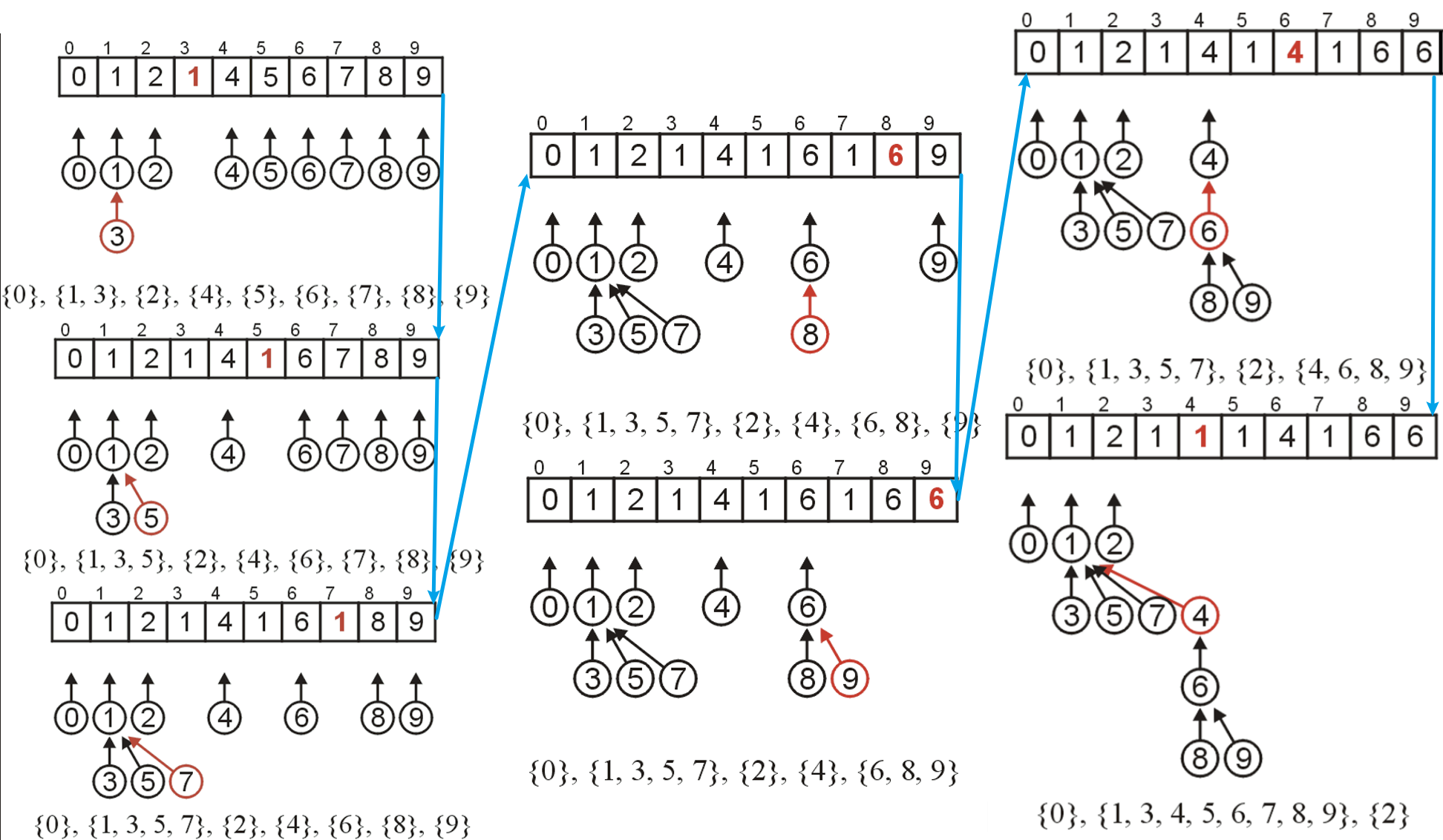
• 若想合并两个集合，则需知道这两个集合的根节点的位置，比如i和j，若想将前者后应集合合并到前者集合内，则只需将parent[j]的值改为i即可，这样j节点下的所有子节点在使用Find回溯根节点时就会回溯到i处，即就完成了合并

• 代码实现如下，该函数时间复杂度为$2\cdot O(h) = O(h)$，和Find一样

void DisjointSetUnion::Union(size_t _idx1, size_t _idx2)
{
    //将第二个索引节点所属集合并入第一个索引节点所属集合
    parent[Find(_idx2)] = Find(_idx1);

    // //确保两个索引处的元素是根节点
    // _idx1 = Find(_idx1);
    // _idx2 = Find(_idx2);
    // //将_idx2所属集合合并到_idx1所属集合上
    // if (_idx1 != _idx2)
    //     parent[_idx2] = _idx1;
}

2.3 时间复杂度分析优化

2.3.1 按秩合并

• 从代码不难看出影响Find和Union时间复杂度的主要因素就是每个不相交集合对应的树的高度，故我们应当设法降低每个不相交集合对应树的高度
  • 对于Find，可以使用路径压缩优化方法（详见后文）
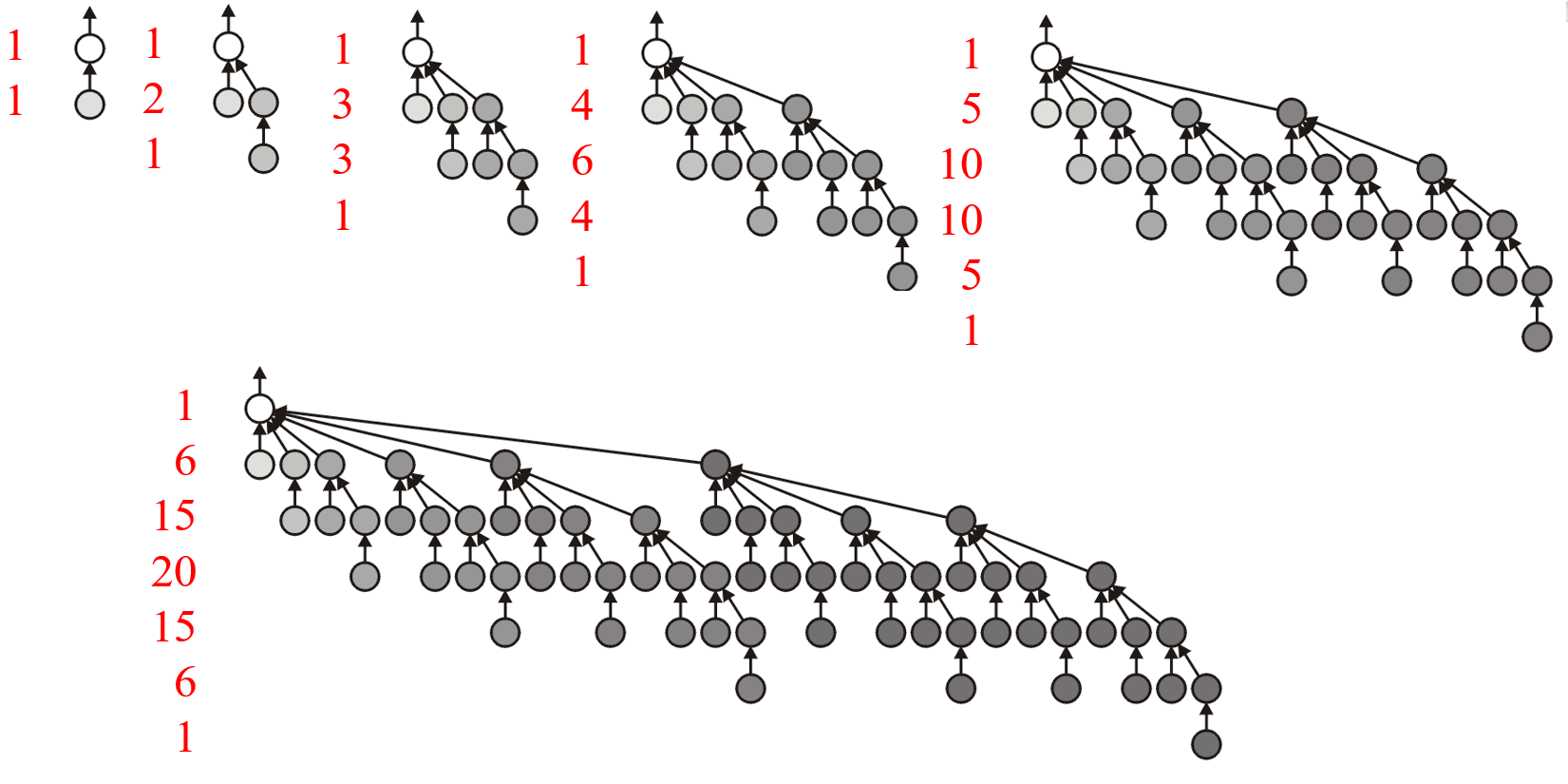
  • 对于Union，可以将较矮的树合并到较高的树的根节点上
    • 该方法最坏情况就是每次合并两个树的高度都相同，这样合并后的树高总会比原先的增高$1$个节点
    • 下图的红色数字表示对应深度的节点数，由此可计算出最坏情况的节点的平均深度为$O(\ln{n})$

• 如下图是节点平均深度为$O(1)$的最好情况；而平均深度为$\Theta(1)$的平均情况较为复杂，可参考此处的解析

• 所谓按秩合并优化就是利用上述思路，由于只有当两树高度相同时，才会在合并时导致树高增加（而一高一低时将矮树挂到高树根节点上并不会增加高度）
• 所以我们可以使用额外一个数组来记录每个节点的秩（Rank），其初始值为$0$，每当某节点遇到被合并挂载了另一个相同高度的树时，就将该值递增，经思考可发现根节点的秩值并不等于其树的高度，但二者间有对应关系，所以秩可被用于比较高度（只有当某节点为根节点时，其秩值才有该意义）

\[\begin{aligned} rank&=0\Rightarrow h = 1 - 1 = 0 \\ rank&=1\Rightarrow h = 2 - 1 = 1 \\ rank&=2\Rightarrow h = 4 - 1 = 3 \\ rank&=3\Rightarrow h = 8 - 1 = 7 \\ rank&=4\Rightarrow h = 16 - 1 = 15 \\ &... \\ rank&=n\Rightarrow h = 2^n - 1 \\ \end{aligned}\]

• 引入了按秩合并的Union代码实现如下

void DisjointSetUnion::Union(size_t _idx1, size_t _idx2)
{
    _idx1 = Find(_idx1);
    _idx2 = Find(_idx2);
    //若归属集合相同，则无需进行后续检查
    if (_idx1 == _idx2) return;
    
    //按秩合并决策树，若树1较矮则挂到树2，若树2较矮则挂到树1
    if (rank[_idx1] < rank[_idx2])
        parent[_idx1] = _idx2;
    else if(rank[_idx1] > rank[_idx2])
        parent[_idx2] = _idx1;
    else
    {
        //秩相等时任意挂接
        parent[_idx2] = _idx1;
        //被挂载根节点对应的秩值递增
        rank[_idx1]++;
    }
}

2.3.2 路径压缩

• 此外也可对Find函数进行路径压缩优化，使得每次调用Find(_idx)时，都将_idx对应元素节点（及其与根节点之间路径上的所有节点）改接到其所在不相交集合的根节点上，而函数Union本身依赖于调用Find函数，每次调用合并也会触发路径压缩
• 路径压缩能使得下次对相同的_idx调用Find的时间复杂度降为$O(1)$，以下是递归实现

//递归的路径压缩优化Find函数
size_t DisjointSetUnion::Find(size_t _idx)
{
    //递归法，集合链极长时可能导致栈溢出，最好采用迭代法
    if (_idx != parent[_idx])
    {
        parent[_idx] = Find(parent[_idx]);
        return parent[_idx];
    }
    else
        return _idx;
}

• 递归法需耗费$O(h)$的函数调用堆栈空间复杂度，因此在遇到较长的集合链时，容易由于递归深度较大而导致栈溢出，所以最好使用如下的迭代法实现

size_t DisjointSetUnion::Find(size_t _idx)
{
    //迭代法，先获取根节点索引
    size_t _root = _idx;
    while (_root != parent[_root])
        _root = parent[_root];
    //然后再压缩路径
    while (_idx != _root)
    {
        size_t _backup = parent[_idx];
        parent[_idx] = _root;
        _idx = _backup;
    }
    //最后返回根节点索引
    return _root;
}

• 路径压缩优化并不能保证所有树的高度都保持为最小的$1$，只能尽量降低每个树的高度，因为将一个根节点并到其它节点上时，其原先的子节点并不会被Find或Union访问到，也就不会触发路径压缩

2.4 综合实现与用例测试

• 以下是并查集类的声明，具体实现上文已给出，也可参考我的代码仓库处

class DisjointSetUnion
{
private:
    //对于元素值等于索引值的元素，其为所在不相交集合的根节点
    //对于元素值等于索引值的元素，其元素值是其父节点的索引值
    std::vector<size_t> parent;

    //用于按秩合并优化，合并时将矮树挂到高树下以降低树的高度
    //只有当某节点为根节点时，其秩值才有意义，用于衡量其树高度
    std::vector<size_t> rank;

    //缓存不相交集合的数量
    size_t setNum;

public:
    DisjointSetUnion(size_t);        //并查集中元素的个数
    
    size_t Find(size_t);             //路径压缩优化，查询某个元素所处不相交集合的根节点
    void Union(size_t, size_t);      //按秩合并优化，合并两个不相交集合集为一个新的集合

    size_t GetSetNum() const;        //获取并查集中不相交集合的数量
    void Print() const;              //打印内核数组用于测试，特别标注根节点
};

• 我们对该类进行测试，请留意下述代码中对程序输出的多行注释标记（被{}包裹的是不相交集合树的根节点），第一行是实现了路径压缩但未实现秩合并优化的输出，第二行则是前者基础上实现了按秩合并的输出，自行体会二者的差异

void MainTest()
{
    //开辟一个包含10个元素的并查集
    DisjointSetUnion dsu(10); dsu.Print();
    //{0} {1} {2} {3} {4} {5} {6} {7} {8} {9}
    //测试下Find函数
    std::cout << "**dsu.Find(2)\n"; std::cout << dsu.Find(2) << "\n";
    //2

    //测试下Union函数
    std::cout << "**dsu.Union(0, 1)\n"; dsu.Union(0, 1); dsu.Print();
    //按秩合并优化前：{0}  0  {2} {3} {4} {5} {6} {7} {8} {9}
    //按秩合并优化后：{0}  0  {2} {3} {4} {5} {6} {7} {8} {9}
    std::cout << "**dsu.Union(1, 2)\n"; dsu.Union(1, 2); dsu.Print();
    //按秩合并优化前：{0}  0   0  {3} {4} {5} {6} {7} {8} {9}
    //按秩合并优化后：{0}  0   0  {3} {4} {5} {6} {7} {8} {9}
    std::cout << "**dsu.Union(9, 8)\n"; dsu.Union(9, 8); dsu.Print();
    //按秩合并优化前：{0}  0   0  {3} {4} {5} {6} {7}  9  {9}
    //按秩合并优化后：{0}  0   0  {3} {4} {5} {6} {7}  9  {9}
    std::cout << "**dsu.Union(8, 7)\n"; dsu.Union(8, 7); dsu.Print();
    //按秩合并优化前：{0}  0   0  {3} {4} {5} {6}  9   9  {9}
    //按秩合并优化后：{0}  0   0  {3} {4} {5} {6}  9   9  {9}
    std::cout << "**dsu.Union(7, 0)\n"; dsu.Union(7, 0); dsu.Print();
    //按秩合并优化前： 9   0   0  {3} {4} {5} {6}  9   9  {9}
    //按秩合并优化后： 9   0   0  {3} {4} {5} {6}  9   9  {9}
    std::cout << "**dsu.Union(1, 3)\n"; dsu.Union(1, 3); dsu.Print();
    //按秩合并优化前： 9   9   0   9  {4} {5} {6}  9   9  {9}
    //按秩合并优化后： 9   9   0   9  {4} {5} {6}  9   9  {9}
    std::cout << "**dsu.Union(2, 9)\n"; dsu.Union(2, 9); dsu.Print();
    //按秩合并优化前： 9   9   9   9  {4} {5} {6}  9   9  {9}
    //按秩合并优化后： 9   9   9   9  {4} {5} {6}  9   9  {9}
    std::cout << "**dsu.Union(4, 9)\n"; dsu.Union(4, 9); dsu.Print();
    //按秩合并优化前： 9   9   9   9  {4} {5} {6}  9   9   4
    //按秩合并优化后： 9   9   9   9   9  {5} {6}  9   9  {9}
    std::cout << "**dsu.Union(1, 5)\n"; dsu.Union(1, 5); dsu.Print();
    //按秩合并优化前： 9   4   9   9  {4}  4  {6}  9   9   4
    //按秩合并优化后： 9   9   9   9   9   9  {6}  9   9  {9}
    std::cout << "**dsu.Union(6, 0)\n"; dsu.Union(6, 0); dsu.Print();
    //按秩合并优化前： 4   4   9   9   6   4  {6}  9   9   4
    //按秩合并优化后： 9   9   9   9   9   9   9   9   9  {9}

    //测试下Find函数
    std::cout << "**dsu.Find(0)\n"; std::cout << dsu.Find(0) << "\n";
    //按秩合并优化前：6
    //按秩合并优化后：9
    dsu.Print();
    //按秩合并优化前： 6   4   9   9   6   4  {6}  9   9   4
    //按秩合并优化后： 9   9   9   9   9   9   9   9   9  {9}
}