浅析多路搜索树与B+树

一、多路搜索树

1.1 基本定义

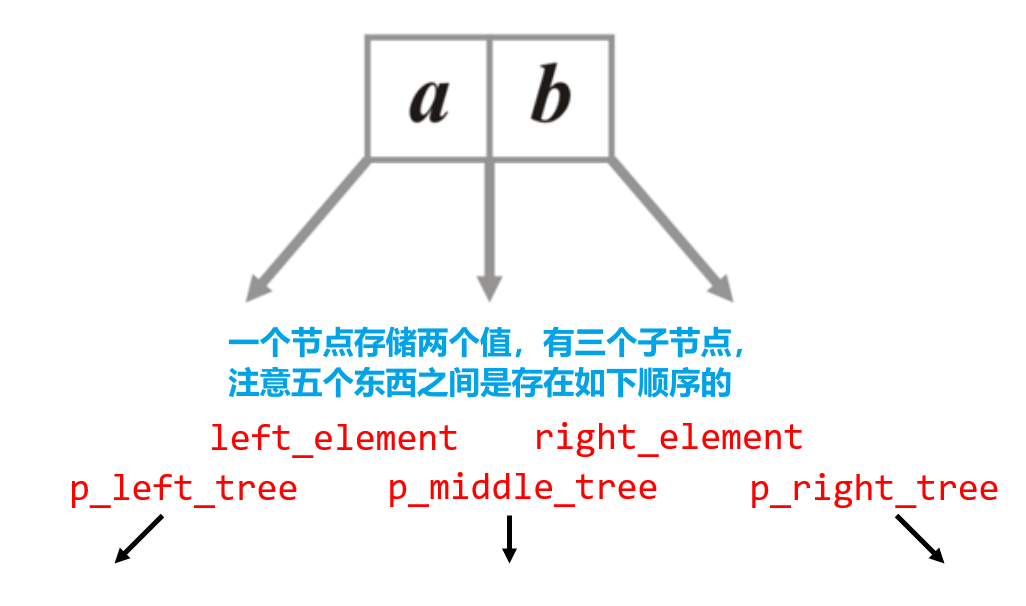
• 以3-Way Tree为例，其每个节点存储两个值，拥有三个子节点，并且满足以下性质
  • 节点存储的第一个值小于第二个值，即$a<b$
  • 每个三路搜索树节点的子树都应该是三路搜索树
  • 左子树内的任意值小于$a$的值，中子树内的任意值在$[a,b]$范围内，右子树内的任意值大于$b$
  • 节点若只存在单个值，则认为该节点为空，新插入的值将被存储在该节中，至于是第一值位置还是第二值位置，则需要比较大小（一般不添加相等的重复值）

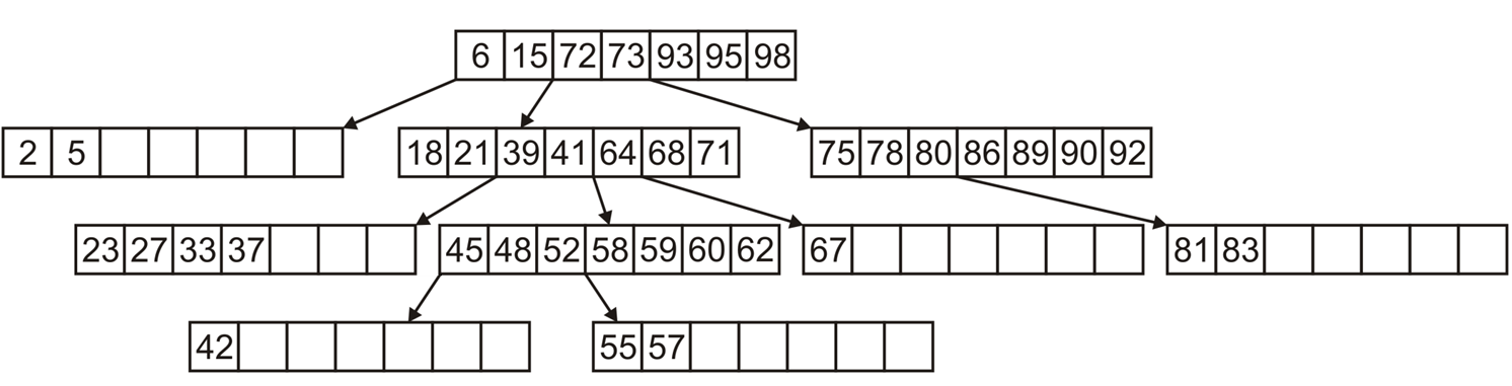
• 推广到8-Way Tree如下所示

1.2 基本操作

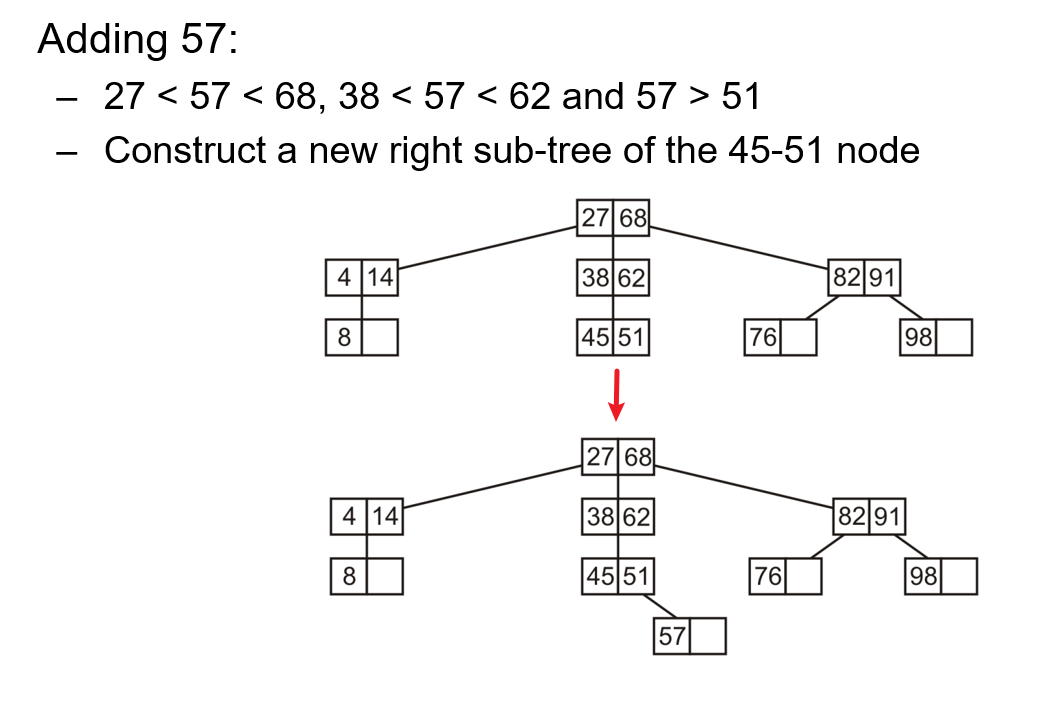
• 其插入值和删除值相较二叉搜索树更为复杂

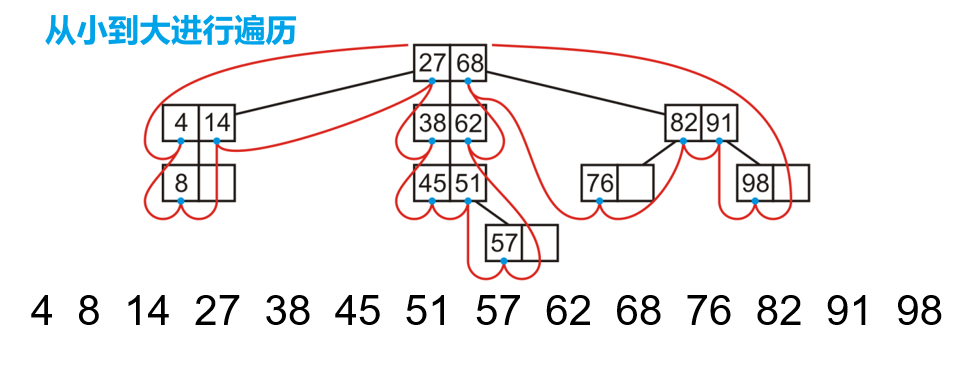
• 其从小到大进行遍历的顺序如下图所示

1.3 存储容量

1.3.1 数据存储总量

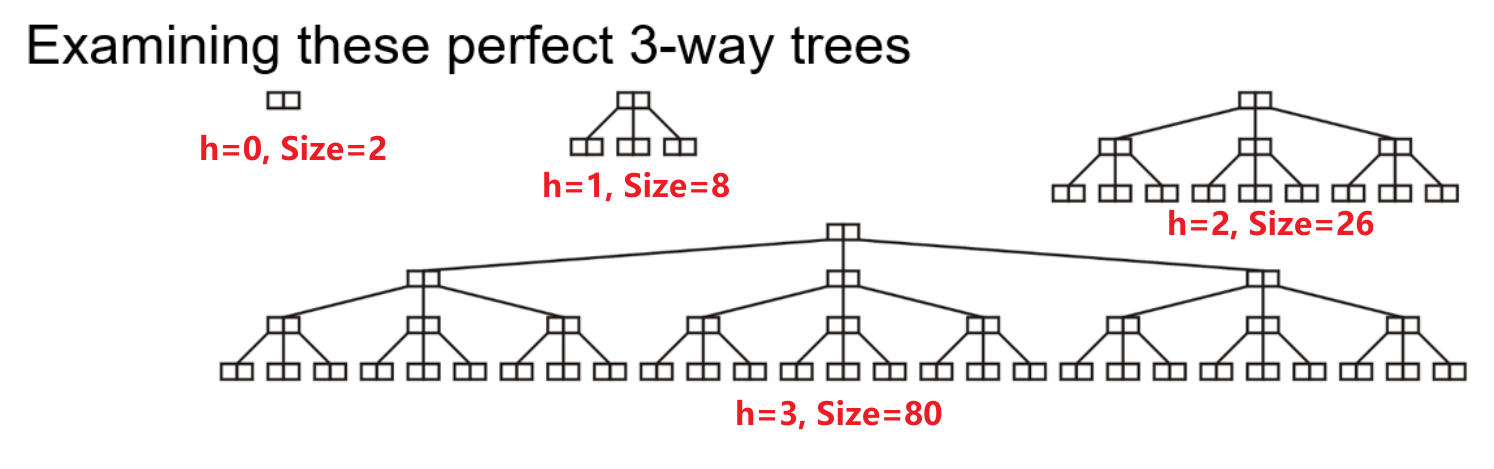
• 完美三叉搜索树的节点总数为$n=\frac{3^{h+1}-1}{2}$，其可存储的值的总数为$n’=3^{h+1}-1$

• 高度为$h$的完美N叉搜索树的叶节点个数为$N^h$个，等比数列求和即可得到高度为$h$的完美N叉树的节点总数为$n=\frac{N^{h+1}-1}{N-1}$，由于N路搜索树的每个节点可存储$(N-1)$个值，所以其存储容量为

\[n'=N^{h+1}-1\]

1.3.2 叶节点的数据存储量占比

• 多路搜索树的叶节点总数为$N^h$，所有叶节点存储的数据总量为$N^h(N-1)$，这些数据占总数据存储量的比例为

\[\frac{N^h(N-1)}{N^{h+1}-1}=\frac{N-1}{N-\frac{1}{N^h}}\approx\frac{N-1}{N}\]

1.3.3 分支路数的选择

• 分支数$N$越大，从根节点搜索到目标结点的路径就越短，但是节点的复杂度就会提高，只有当节点之间的跳跃成本十分高的时候（比如硬盘的Block间的跳跃就很耗时），才值得我们去牺牲复杂度来换取更低的搜索路径

二、B+树

2.1 背景引入

2.1.1 硬盘与内存的对比

• 对比内外存的容量大小与读写速度，差异巨大
  • Cache：内存，KiB-MiB，速度$1$GHz
  • 主存：内存，MiB-GiB，速度$100$MHz
  • 硬盘：外存，GiB-TiB，速度$100$Hz（搜索每个Block耗时$10$ms）

• 造成容量和速度不可兼得的底层原因是
  • 主存处于存储器层次结构的上层，一般是以字节为单位进行寻址的，要找到某bit的数据就得先找到其所在字节，而暂未被利用的剩余七bit数据并不会占用太多性能与空间
  • 硬盘处于存储器层次结构的下层，是以Block为单位进行寻址的，每查找一个Word的数据就得加载整个Block的数据，暂未被利用的数据耗费的性能与空间会更大，导致读写速度更慢
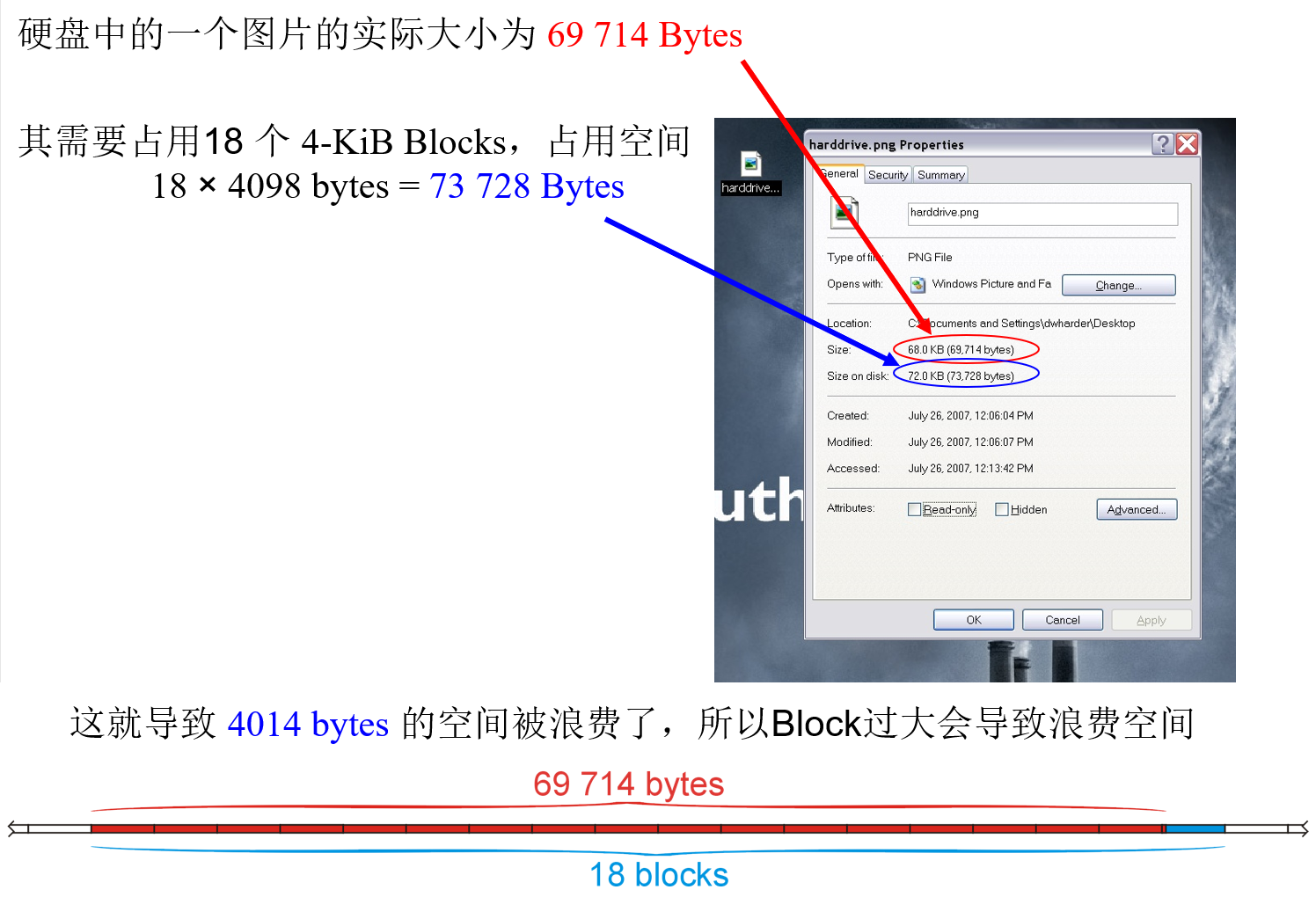
• 电脑硬盘中的文件会占用整数个Block的空间用于存储自身，即文件占用的空间大小实际上是大于自身的实际大小的（从而导致空间的浪费），如下图示例所示

2.1.2 二叉搜索树存储巨量数据

• 试想一种场景：我们需要在硬盘中长久存储$10^9$个数据，每个数据的键的大小为$4$字节（假设先不考虑存储键对应的值），每个数据还需保存一个指向子节点的的$4$字节的指针（即 $32$bit的编码，其可被解码出$2^{32}$个不同的地址）

• 如果我们用二叉搜索树对其进行存储的话，树高就为$[\log_{2}{(10^9)}]=[29.89]=29$，若我们想要寻找一个在叶节点处（即最坏时间复杂度的情况）的数据，并且路径上的每个节点都在不同的Block内的话，我们就需要遍历$29$个Block，而硬盘搜索每个Block的耗时是$10$ms，时间成本巨大

2.1.3 多路搜索树存储巨量数据

假设我们的硬盘的Block大小为$4$KiB

• 因为在Block之间跳跃的成本太高，而二叉搜索树会导致树高过大，所以那我们就尝试实用多路搜索树进行存储，以通过增大节点复杂度来降低树高
• 我们将多个数据（包括其指针）打包放入多路搜索树的单个节点内，每个数据键大小为$4$字节，每个指向子节点的指针大小为$4$字节，粗略计算每个Block可以存放数据的个数为

\[\frac{4Ki}{4+4}=\frac{4\cdot2^{10}}{8}=512\]

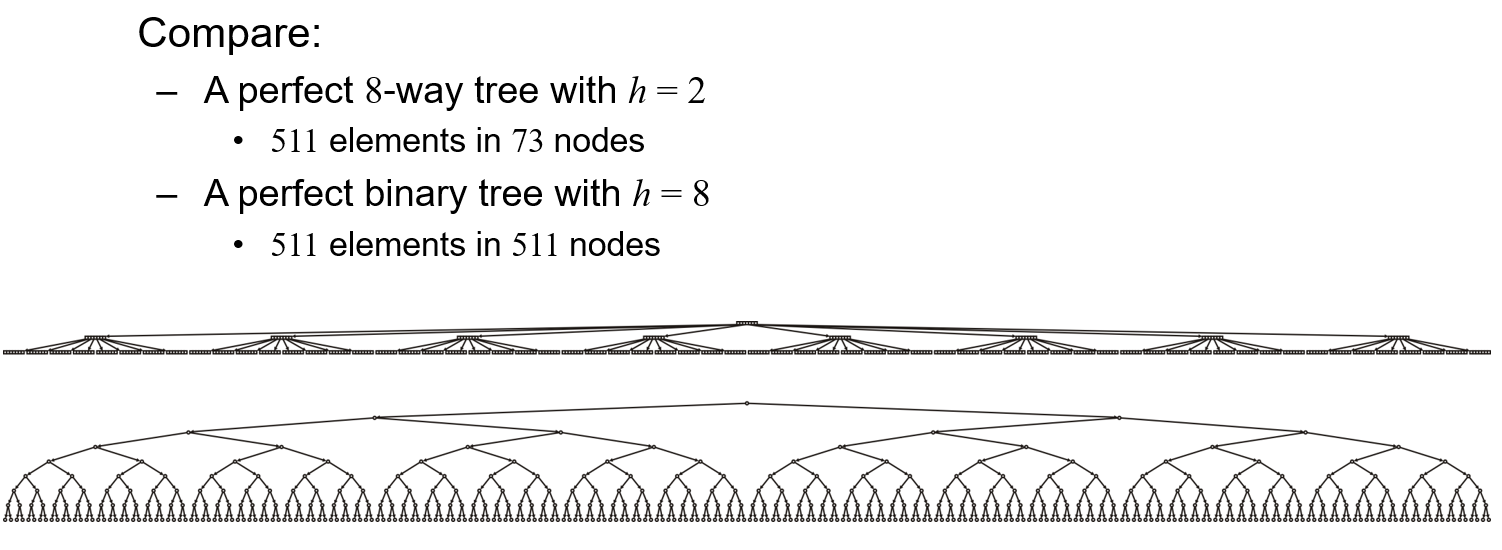
• 由于$M$路搜索树的单个节点只能存放$M-1$个数据，但需要存储$M$个指向子节点的指针，所以上述用$4+4$作分母是少算了一些指针进去的，所以我们只在单个Block内塞入一个含$511$个数据元素的$512$路搜索树的节点，此时的树高可算得为$3$，是二叉搜索树高度$29$的近乎十分之一，其搜索效率自然也就快了近乎十倍

\[[\log_{512}{(10^9)}]=3\]

• 但是此时我们存储的只有数据的键与指针，实际场景中还需要存储键对应的值，假设值大小为$100$比特的话，单个数据的键值就占用共$100+4=104$比特，单个Block可以存放的数据量就约为

\[\frac{4Ki}{104+4}\approx37\]

• 此时我们就可以用$38$路搜索树的单个节点填充一个Block，此时的树高就是$5$了，相比$512$路搜索树的$3$的高度增多了$67\%$的搜索时间，这是我们不想看到的

\[[\log_{38}{(10^9)}]=5\]

• 我们还注意到存在着一些空间的浪费

2.1.4 转移数据至叶节点

• 上述的$38$路搜索树的叶节点存储的数据总量（注意不是叶节点总量）占总存储量的比例为

\[\frac{N^h(N-1)}{N^{h+1}-1}\approx\frac{N-1}{N}=\frac{37}{38}\approx97\%\]

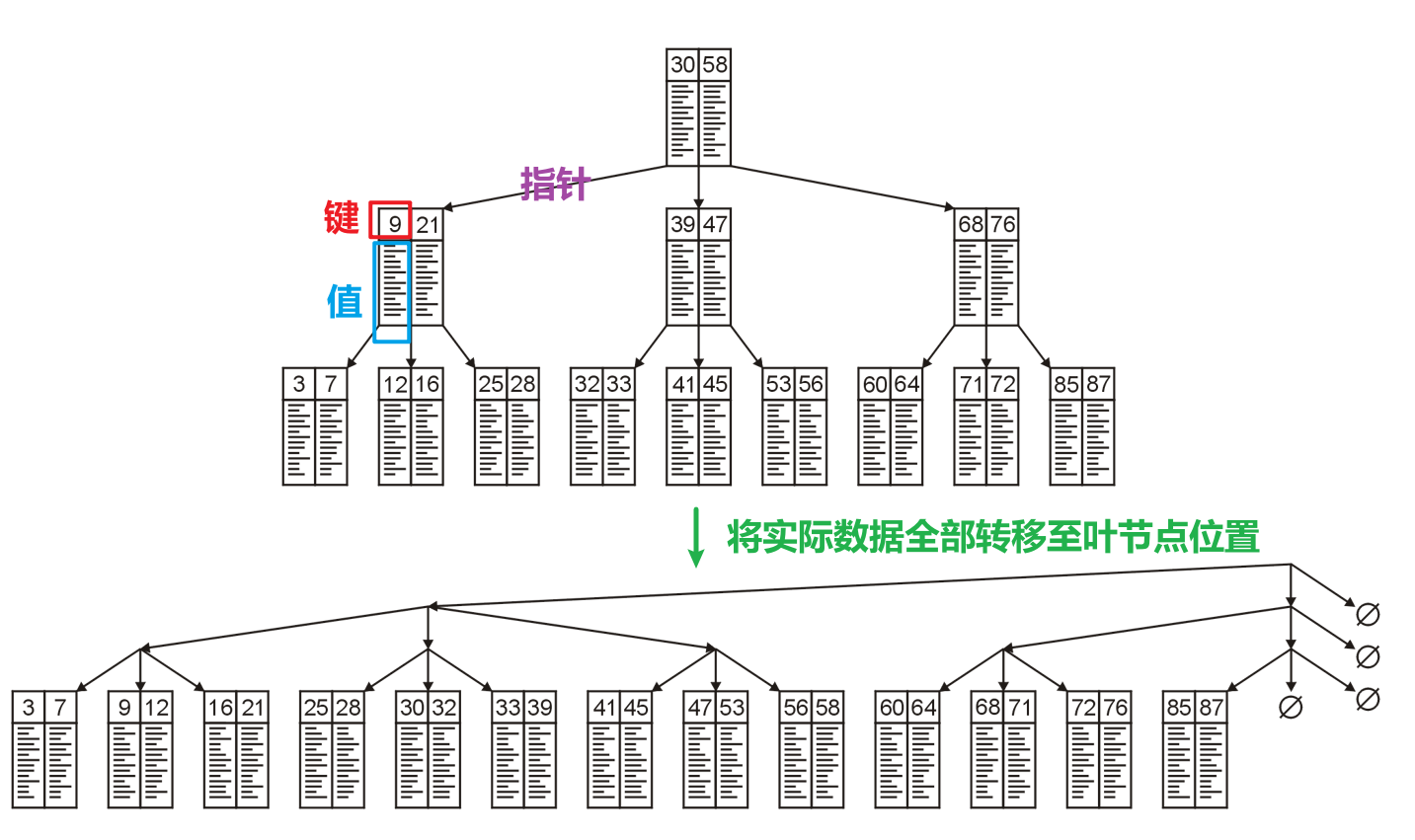
• 所以我们倒不如直接将所有的数据（键值对部分的$104$比特）转移到叶节点上去，如下图我们以$3$路搜索树为例

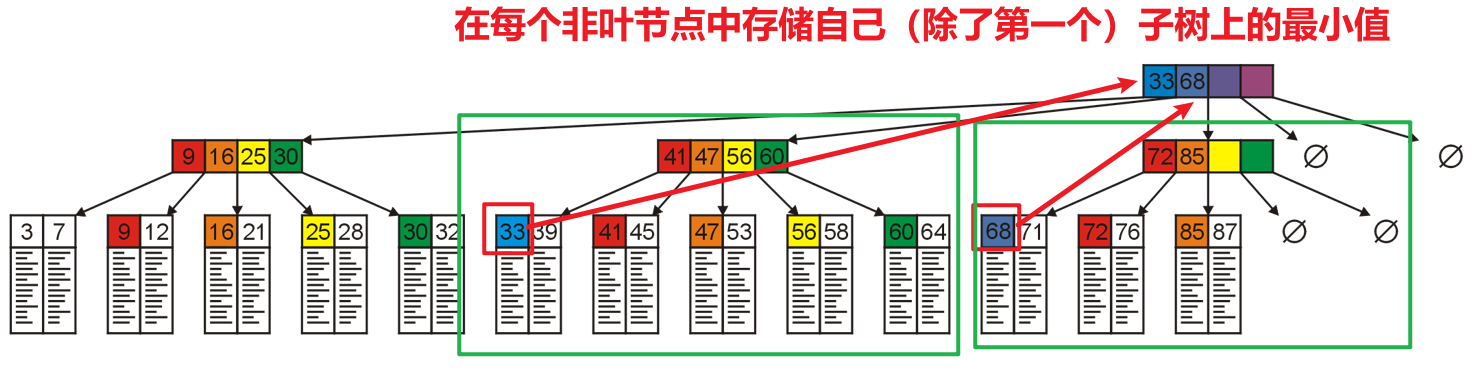
• 可是我们仍然需要让每一个节点占一个Block，如果非叶节点不存储键、值、指针三者中最占空间的值的话，那就可以存储更多的键与指针了
• 我们选择用$N$路搜索树的每个非叶节点中的$N-1$个空间，来存储除了第一个子树（因为共$N$个子树，装不下了）外的$N-1$个子树中的最小键

• 这就是B+树的雏形，但是B+树增加了一些别的限制

2.2 定义与形式

B+树是针对存储在硬盘中的数据的，而AVL树、红黑树等都是假定数据存储在主存中的

2.2.1 过渡信息

• B+树并非严格的多路搜索树，而是依据Block的容量大小，分别采用了两种多路搜索树的节点分别作为叶节点和其它节点（内部节点与根节点）
  • 叶节点都只用于存储数据的键与值，采用$N$路搜索树的节点来存储
  • 内部或根节点都只用于存储指向各子树的指针（可能是叶节点即$N$路搜索树节点，也可能是其它内部节点即$M$路搜索树节点）、各子树上的最小键，采用$M$路搜索树的节点来存储
  • 由于值很大，而叶节点或其它节点都存储在同样大小的单个Block内，所以显然$M>N$
• 为了能继续推进，我们限定下文中讨论的Block的容量大小为固定$4$KiB，此时我们需要分别确定$N$与$M$的大小，以保证在单个Block中塞入最多的数据个数

2.2.2 叶节点

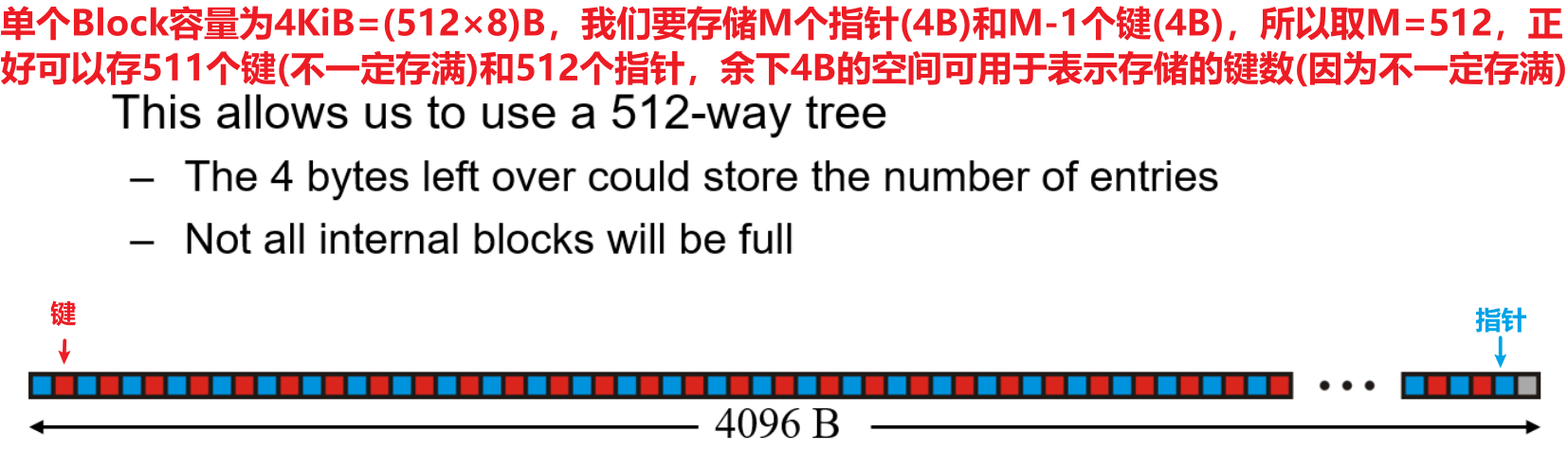
• 假设单个数据由$4$比特的键和$100$比特的值组成，则我们用总容量除以$104$（叶节点无需存储指针，所以不需考虑指针大小）并向下取整得

\[[\frac{4\cdot2^{10}}{104}]=39\]

• 所以$N=40$，即单个Block最多可以使用$40$路搜索树存储$39$个数据的键与值，由于不是整除，所以会有一些剩余的空间（如下图所示，深红色是键，粉色是值，灰色是未利用空间）

2.2.3 内部节点与根节点

• 由于键值对数据的所有值均存在叶节点中，所以B+树的内部节点或根节点只需存储
  • 指向各子树（可能是叶节点也可能是其它内部节点）的指针共$M$个
  • 除了第一个子树外的子树的共$M-1$个最小键（用于快速定位）
• 下面我们分析单个Block用于存储内部节点或根节点而非也节点时，最多可以存多少键与指针

2.2.4 整体形式示意

• 对于不同大小的文件的存储需求，B+树的高度有所改变，假设我们要存储$10^9$个键值对数据
  • 需要$N=40$路搜索树节点即叶节点$\frac{10^9}{39}=25,641,026$个（除法结果已向上取整）
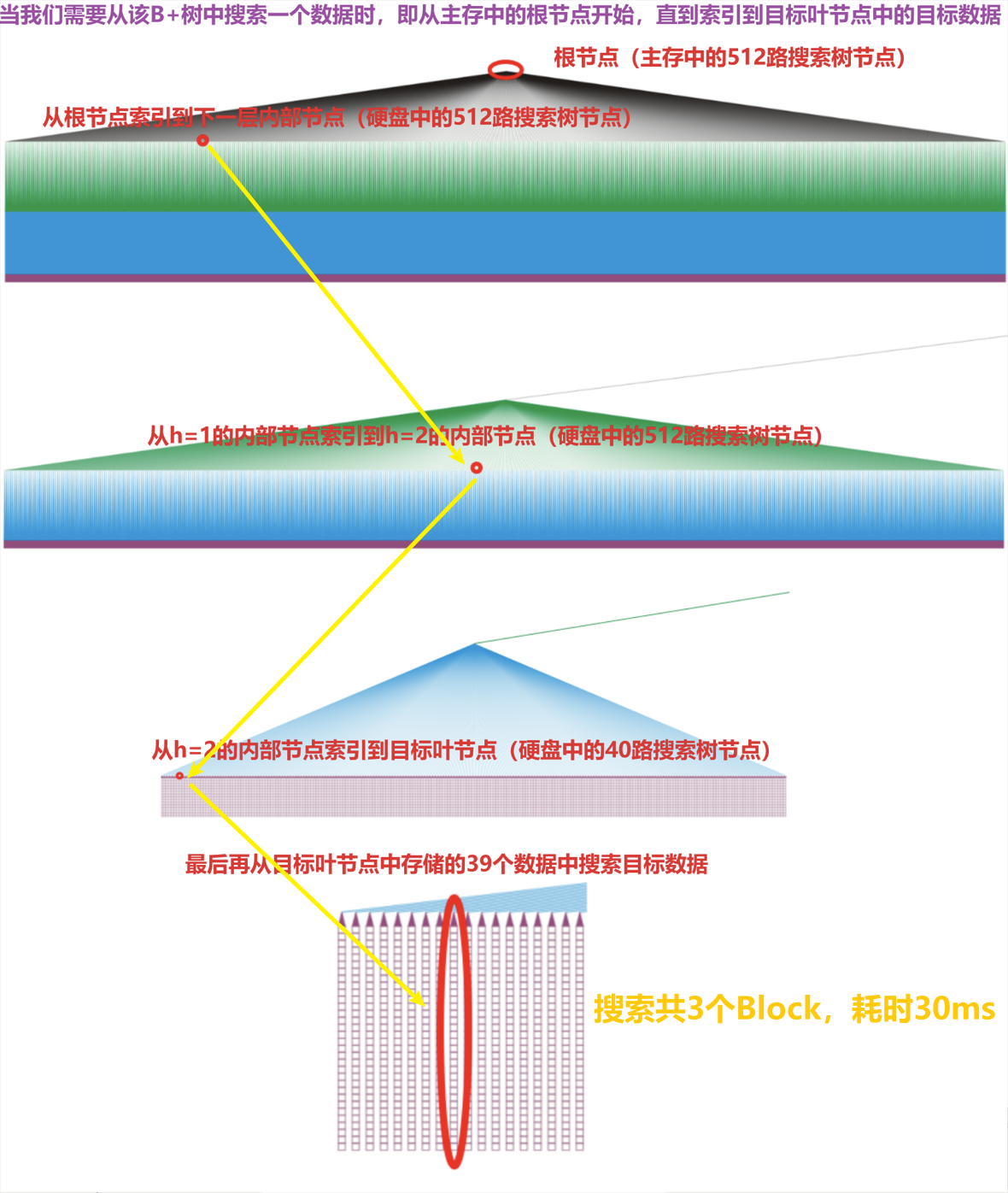
  • 高度为$h$的$M=512$路搜索树下端可以指向$512^{(h+1)}$个叶节点，所以该B+树的上层是个高度为$h=[\log_{512}{25,641,026}]-1=2$的$M$路搜索树，该树下端指向的全部是$N$路搜索树节点
• 算上叶节点，该B+树的高度就为$3$，所有的搜索操作（所有可能的目标都存在叶节点内）都固定需要我们跳跃$3$个Block（B+树的根节点是存储在主存中的，其它Block都在硬盘中），即每次搜索都需要固定$30$ms的延迟

• 为保证每个数据的搜索时间相同，应确保所有叶节点处于同一高度上

2.2.5 一般性定义

• 一个B+树满足以下性质（假设$L=N-1$，其大小取决于Block的容量与键值对数据的尺寸）
  • 若存储的数据总条数不大于$L$
    • 根节点是一个$N$路搜索树节点
  • 否则所有数据都存储在叶节点的$N$路搜索树节点中
    • 根节点是一个$M$路搜索树节点（存储$[2,M]$范围内个指向子树的指针、以及最多$M-1$个除了第一个子树外的子树中的最小键）
    • 其它内部节点是$M$路搜索树节点（存储$[\frac{M}{2},M]$范围内个指向子树的指针、以及最多$M-1$个除了第一个子树外的子树中的最小键）
    • 叶节点至少半满，即叶节点存储的数据条数在$[\frac{L}{2},L]$范围内
    • 所有叶节点处于同一深度
• 对于内部节点和叶节点，如果不填满的话就可能导致树高增大，但某些情况下最坏的填充率（填一半）与全填满得到的树的高度是一样的，此时就无需全部填满

2.2.6 与B树的区别

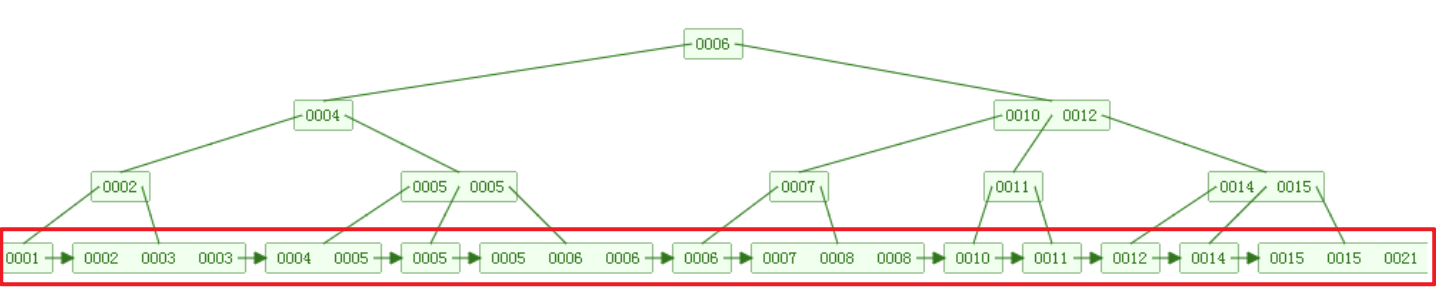
• B+树的实际数据仅存储在叶节点中，其余节点中仅存放用于搜索的键和指向子节点的指针，在我们推导出B+树这样的结构之前，数据是可以被被完整地存储在任意（多路搜索树）节点上的，这就是B树（或称B-树，注意-不是减号，只是一个连接符而已）
• B+树是B树的优化变种，在B树中，键大小相邻的数据之间可能并不是物理意义上相邻的；而在B+树中，由于数据都存储在叶节点中，并且我们会将所有叶节点的数据键链接成一个线性的结构以方便查找相邻的元素（在后面对B+树的各种操作中会详细讲），如下图所示

2.3 查找操作

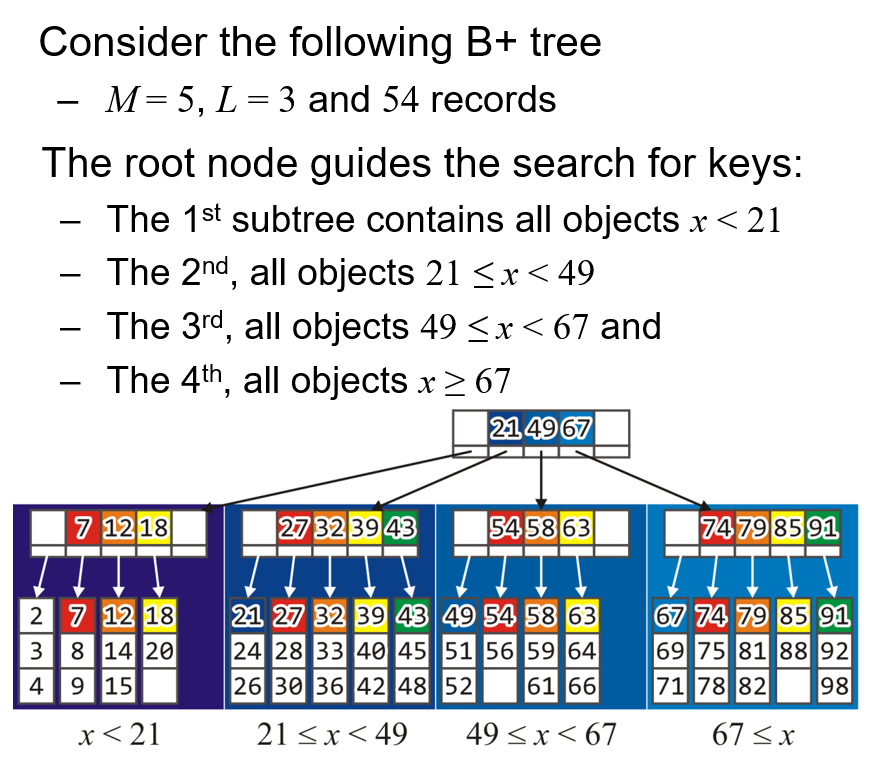
• 为了简化展示，我们选取的演示对象为一个$h=2,M=5,N=4$的未完全填满的B+树

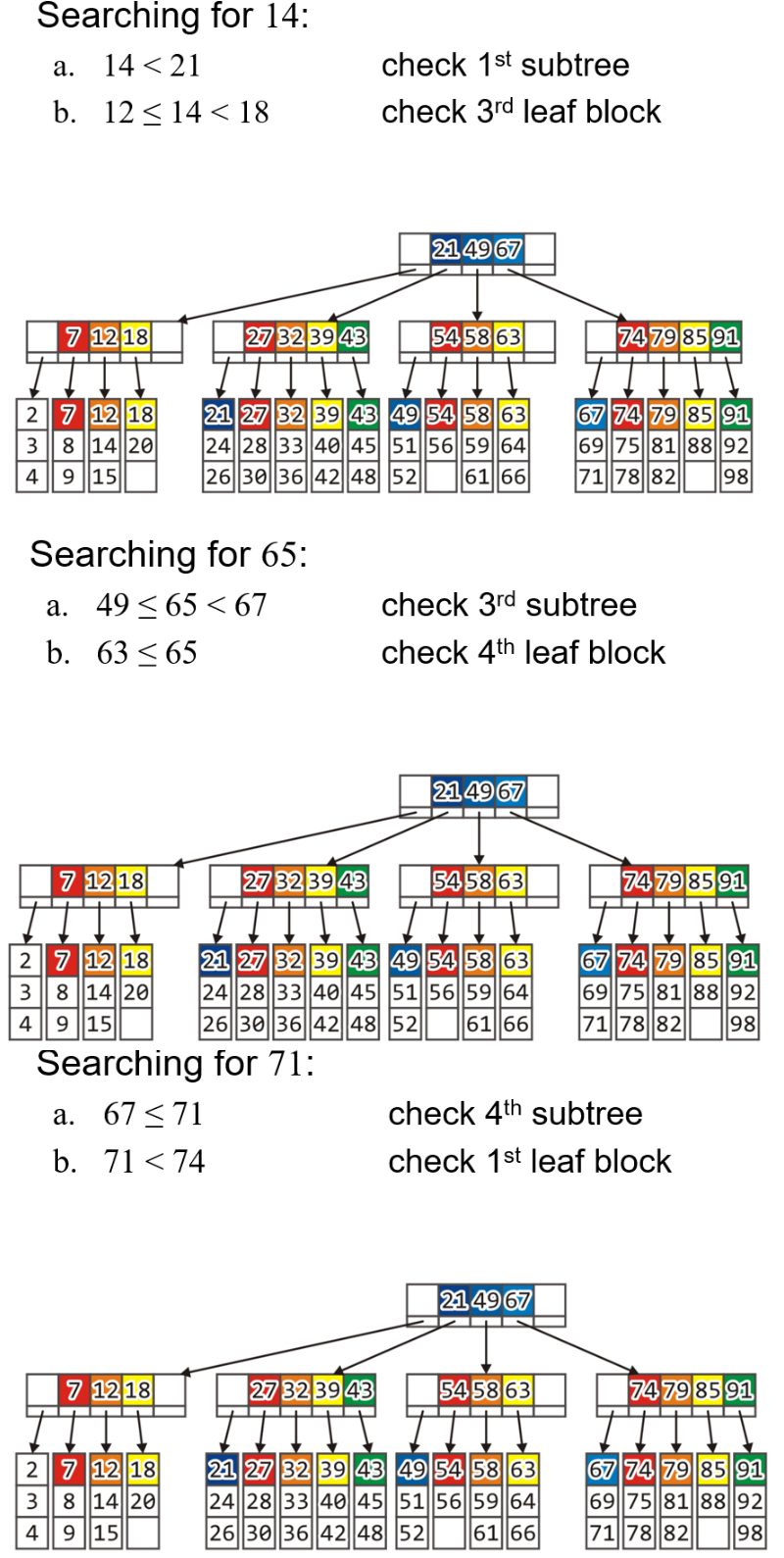
• 我们查找该B+树中的某一节点，从主存中的根节点开始，按照多路搜索树的搜索方法搜索即可

2.4 插入操作

2.4.1 叶节点有空位

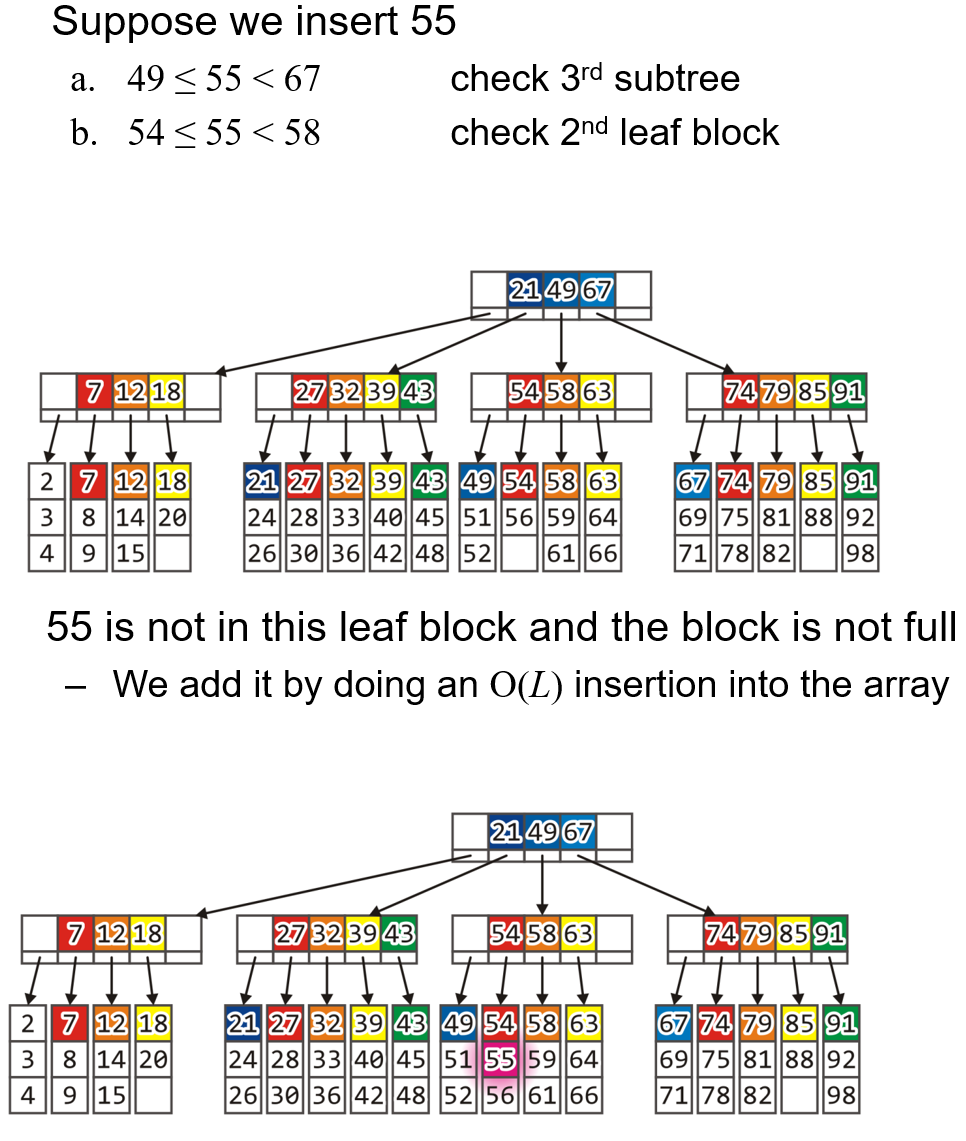
• 按照和查找操作一样的方法找到被插入对象应当被插入的位置，若有空位则直接插入并保存

• 上述操作耗时：$20$ms（历经两个Block搜索到目标叶节点）+$10$ms（遍历叶节点Block）=$30$ms

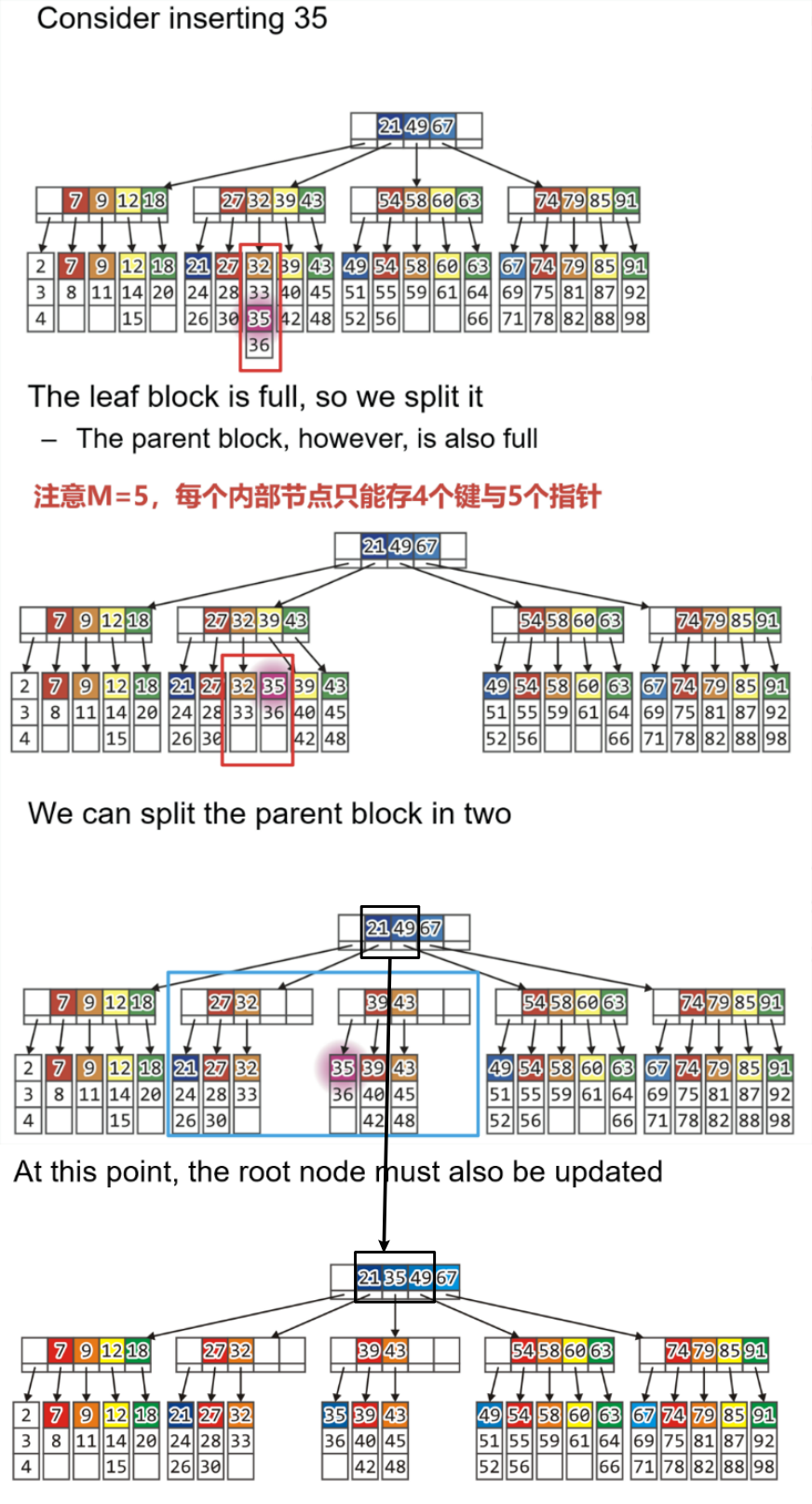
2.4.2 叶节点无空位

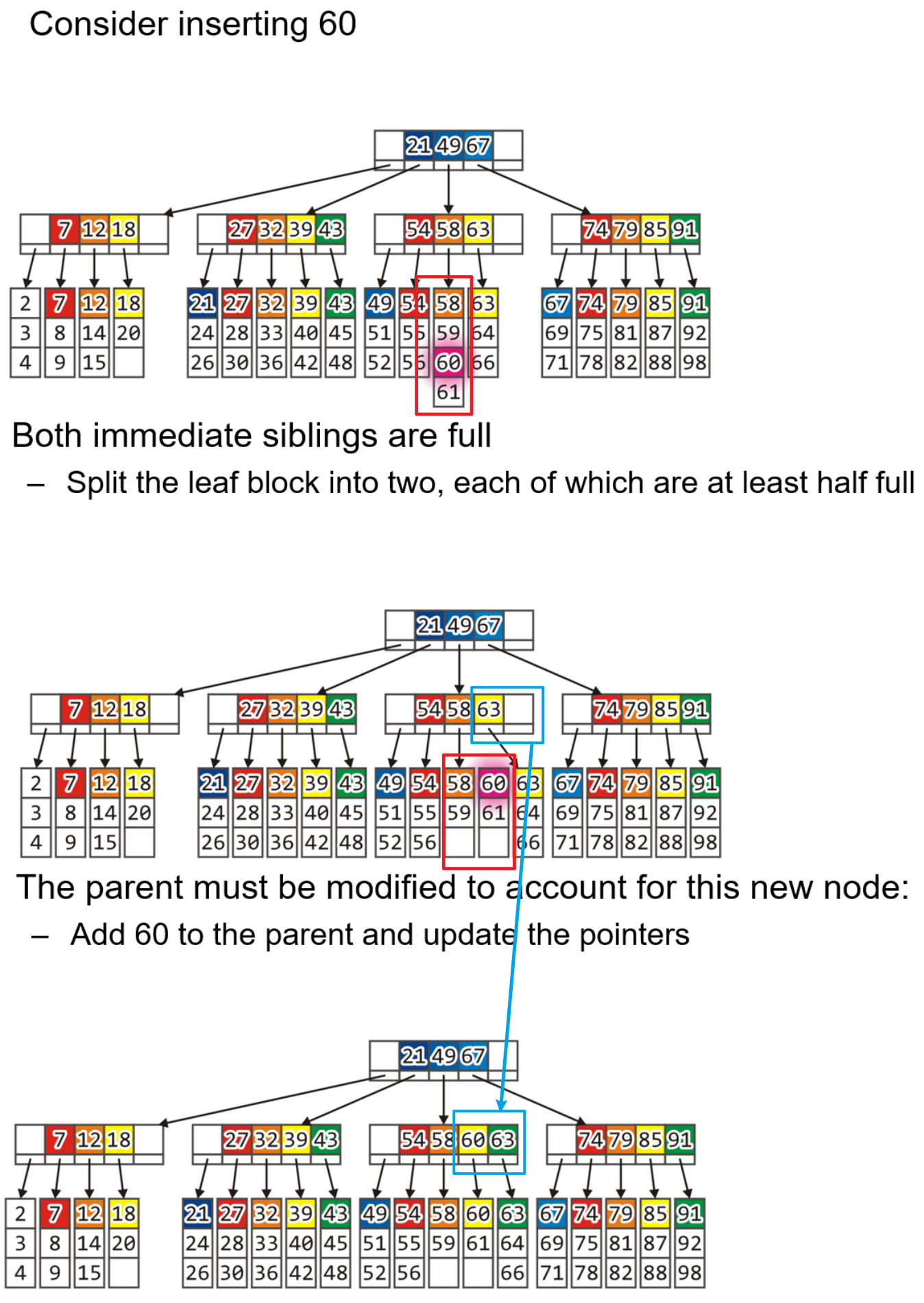
• 若目标的叶节点Block已满，则将该叶节点连同其内数据对半分为两个叶节点，这样这俩叶结点存储的数据就是$\frac{L}{2}$了（我们应当保证每个叶节点都至少是半满的）
• 插入完后还应当对目标叶节点的父节点储存的键进行更新保存

• 上述操作耗时：$20$ms（搜索到目标叶节点）+$20$ms（处理分裂的两个叶节点Block）+$10$ms（更新父节点）=$50$ms

2.4.3 父节点也无空位

• 若目标叶节点的父节点也满了，则需先将叶节点对半分，然后再递归至父节点的父节点，将父节点也进行对半拆分复制

• 上述操作耗时：$20$ms（搜索到目标叶节点）+$20$ms（分裂叶节点）+$20$ms（分裂父节点）+$10$ms（更新祖父节点）=$70$ms

2.4.4 直到根节点也满了

• 如果像之前那样一直递归下去，直到根节点也满了，那就需要增加树的高度了

• 上述操作的耗时：$70$ms+$20$ms（拆分根节点为两个Block，放入硬盘中，新的根节点在主存中所以此处加上的不是$30$而是$20$ms）=$90$ms

2.5 删除操作

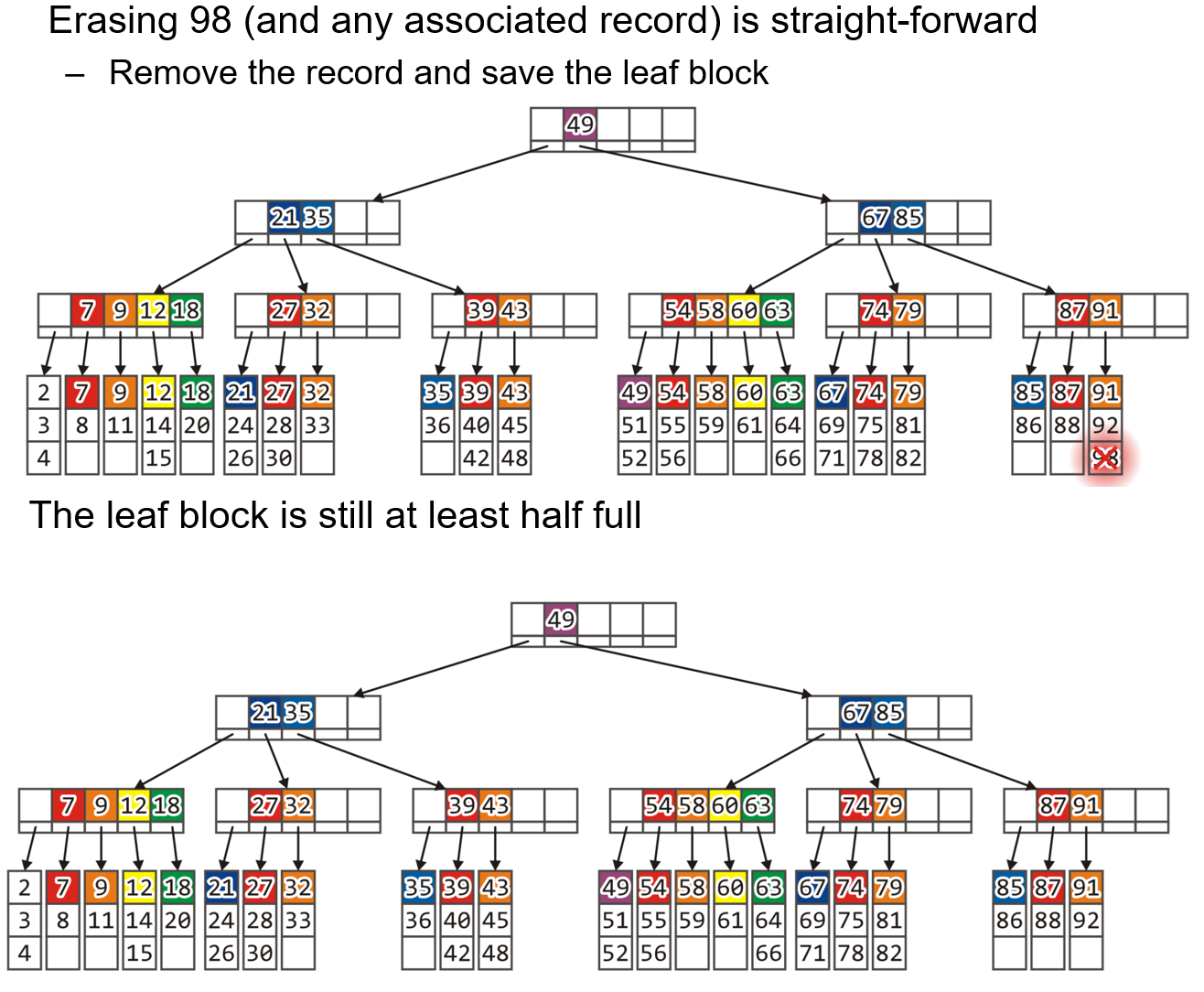
2.5.1 普通情况

• 删除叶节点中的一个数据后，若该叶节点内的数据条数仍然大于等于半满，且该叶节点中的最小键没有改变，则啥也不用干

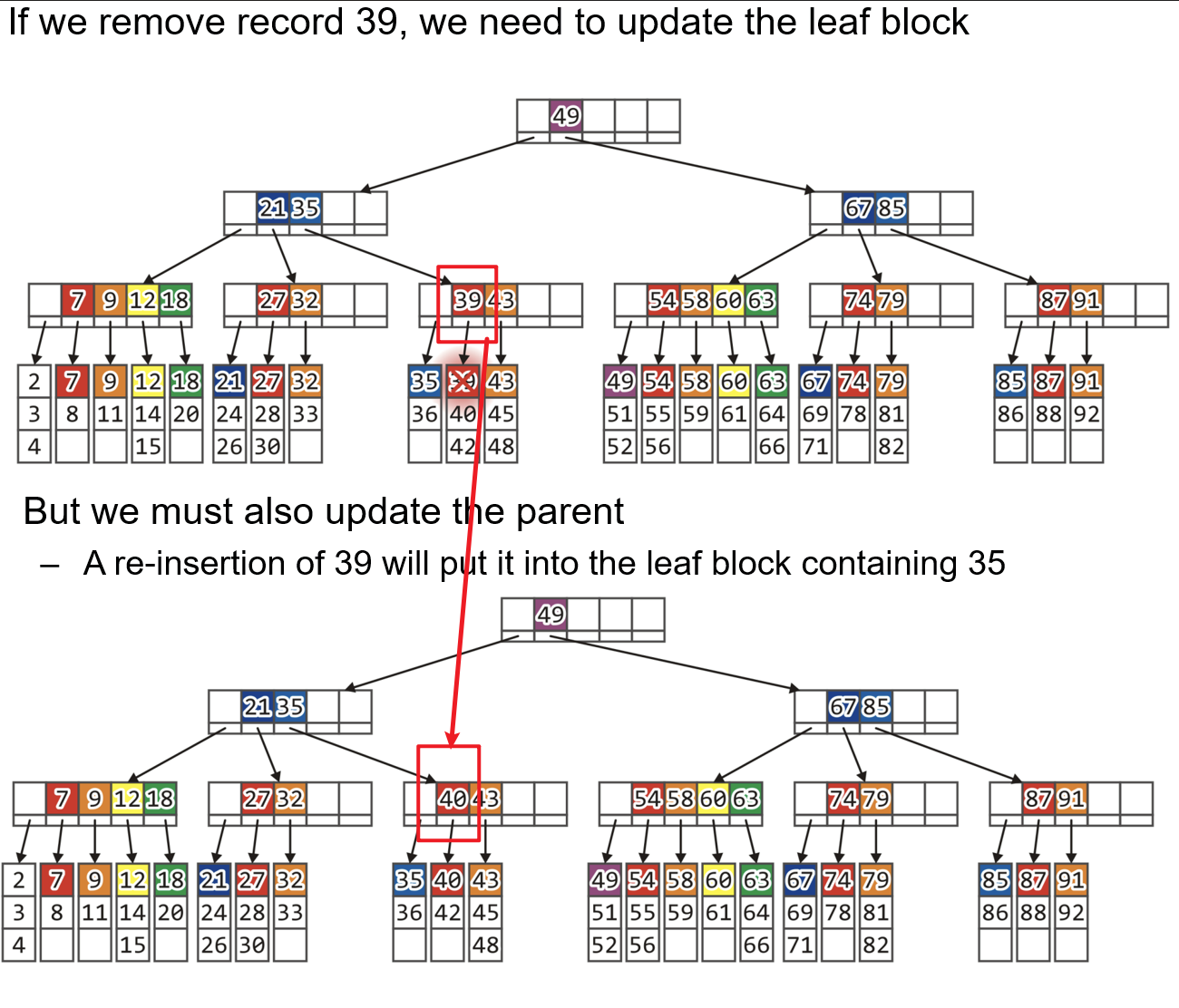
• 若最小键发生了变化，则需要更新父节点

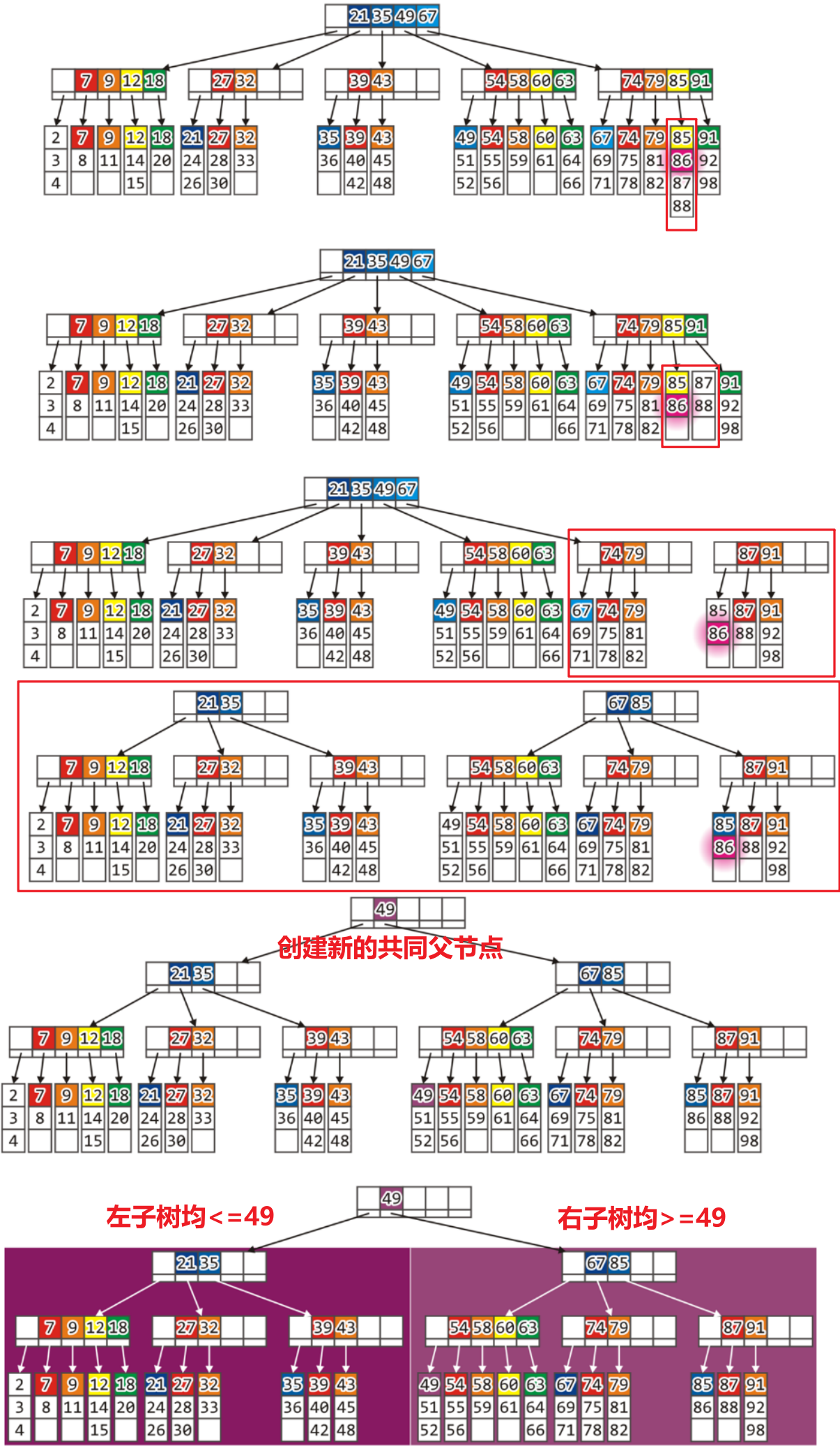
2.5.2 叶节点需合并的情况

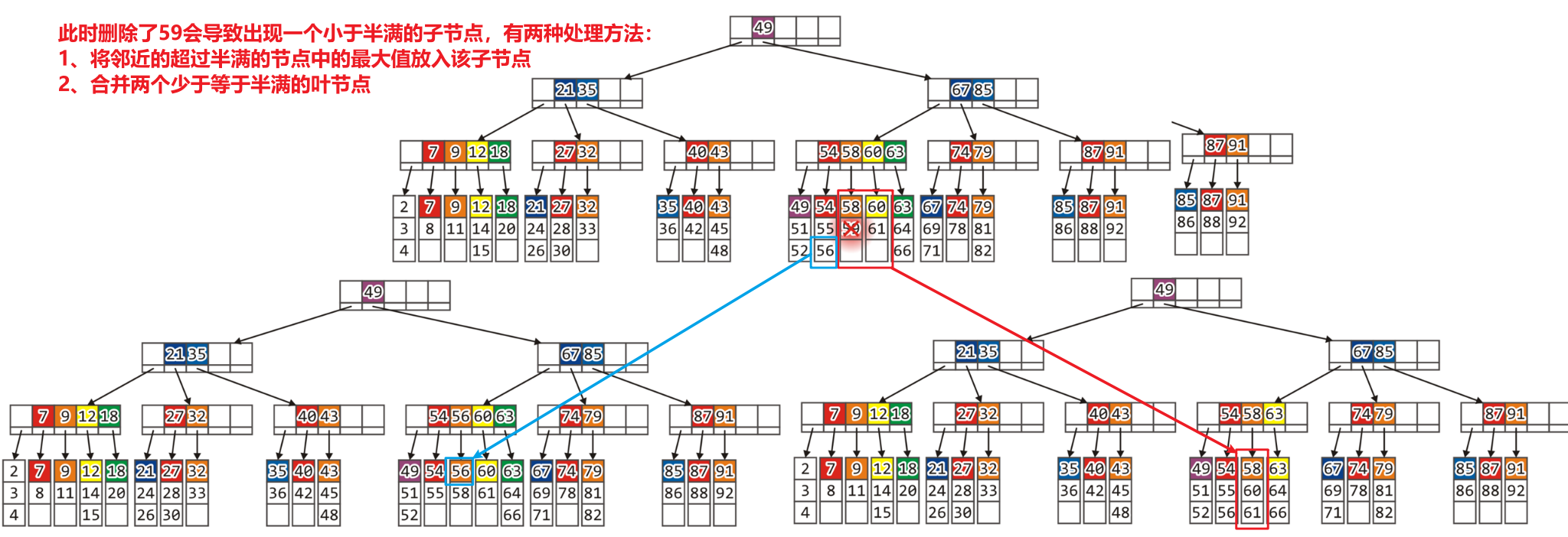
• 当我们删除了叶节点中的若干数据后，若此时树中出现了储存数据数$<=\frac{L}{2}$的叶节点
  • 若只有单个叶节点如此，则可用稍满的左侧某叶节点的最大值（或右侧某叶节点的最小值）到自己身上
  • 若有两个叶节点如此，则可以将二者合并，以保证二者储存的数据条数均在$[\frac{L}{2},L]$范围内

• 合并的话，最好选取处于同一父节点下的两个小于半满的叶节点，这样可以降低操作的耗时；我们之前讲过，B+树的叶节点存储的数据都会被从左到右（即键从小到大）串成一个线性结构（一般是单向链表或双向链表），这样我们就可以很方便地找到相邻的非半满叶节点进行合并了

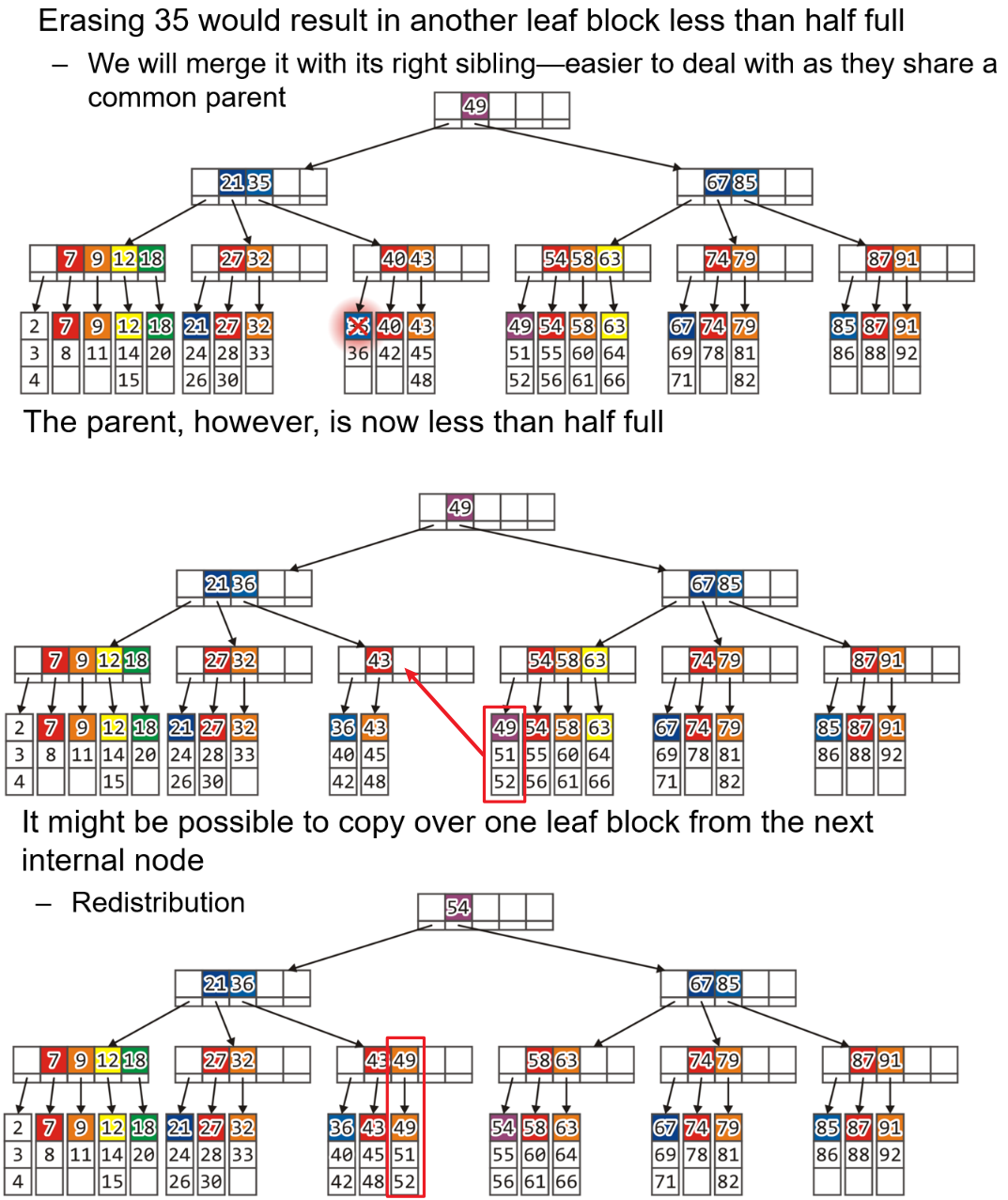
2.5.3 父节点需合并的情况

• 若多个内部节点的子节点数$<=\frac{M}{2}$，那么同理也需要进行转移同深度的较满的内部节点的子节点到自己身上，或者合并父节点的操作
• 下图是转移子节点的方式示意，这样得到的结果不如合并那样能带来高度的降低

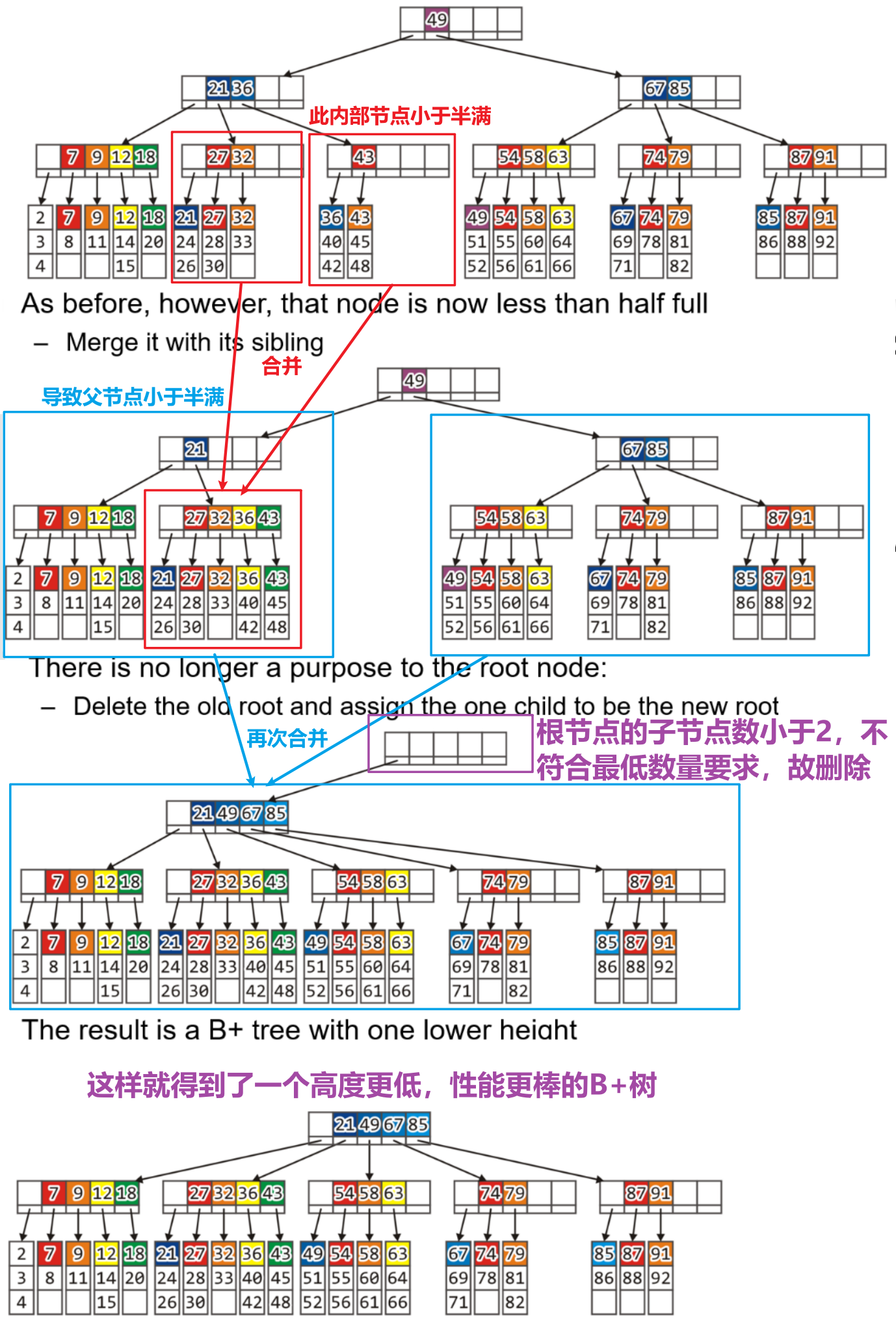
• 对于上述情况，我们还可以进行非半满内部节点的合并，此情况下我们得到了高度更低的树