最短路径之Dijkstra算法

一、关于最短路径

• 最短路径问题就是关于加权图中的两个顶点间的最小总权路径的寻找的问题

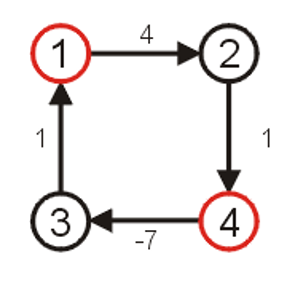
• 一般来说最短路径问题中的图中的边应当全部为非负，否则可能出现可以在某个环上不断寻来减少总路径权重的情况，如下图的环，每绕一圈总权减少$1$

• 通常应用于游戏AI寻路、电路设计、导航等一系列类似问题中

二、Dijkstra算法

图示算法参考此视频

2.1 算法思路

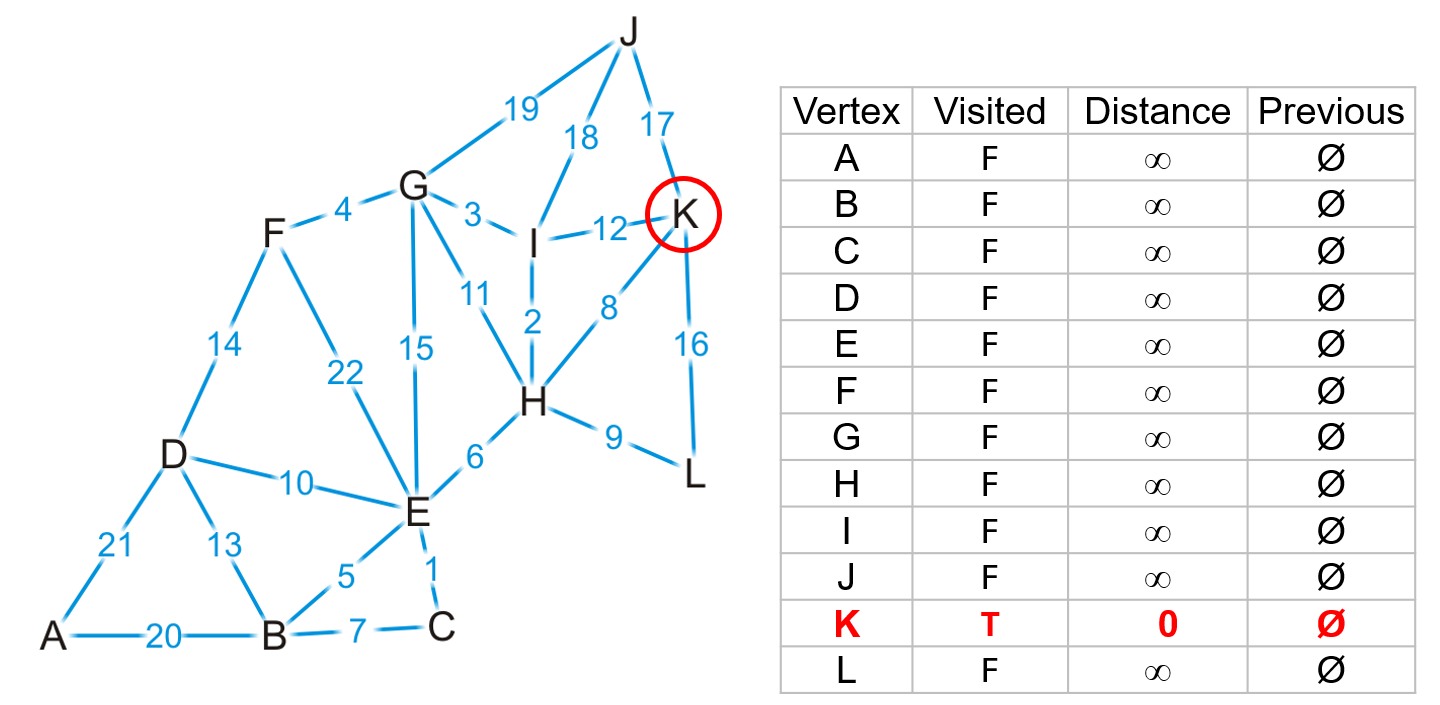
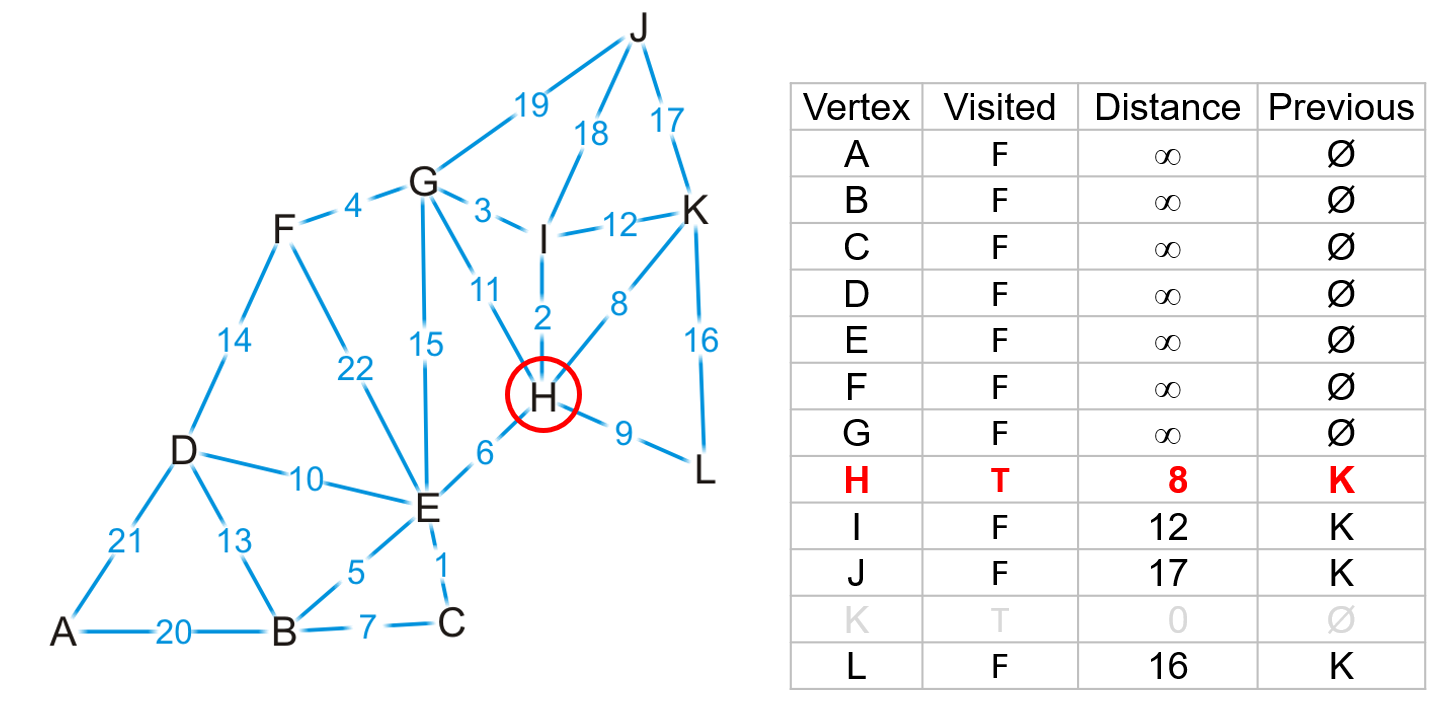
• 对于下图中的加权图，我们需要寻找$K$顶点到其它任意顶点的最短路径，可以使用一个类似Prim算法中的列表，存储元素为std::tuple<bool,float,Vertex*>元组，Dijkstra算法需要遍历所有顶点（共$|V|$次）进行检查，每检查一个顶点都会更新其所有邻接顶点的最短路径和前驱顶点
  • 布尔值用于记录该顶点当前是否已找到了最短路径
  • 浮点值表示从$K$到该顶点的最短路径的长度
  • 顶点指针表示从$K$到该顶点的最短路径中，该顶点的前驱顶点是谁
• 从起始顶点$K$开始，$K$到自身的最短路径长度为$0$，初始化为(true,0,nullptr)即可

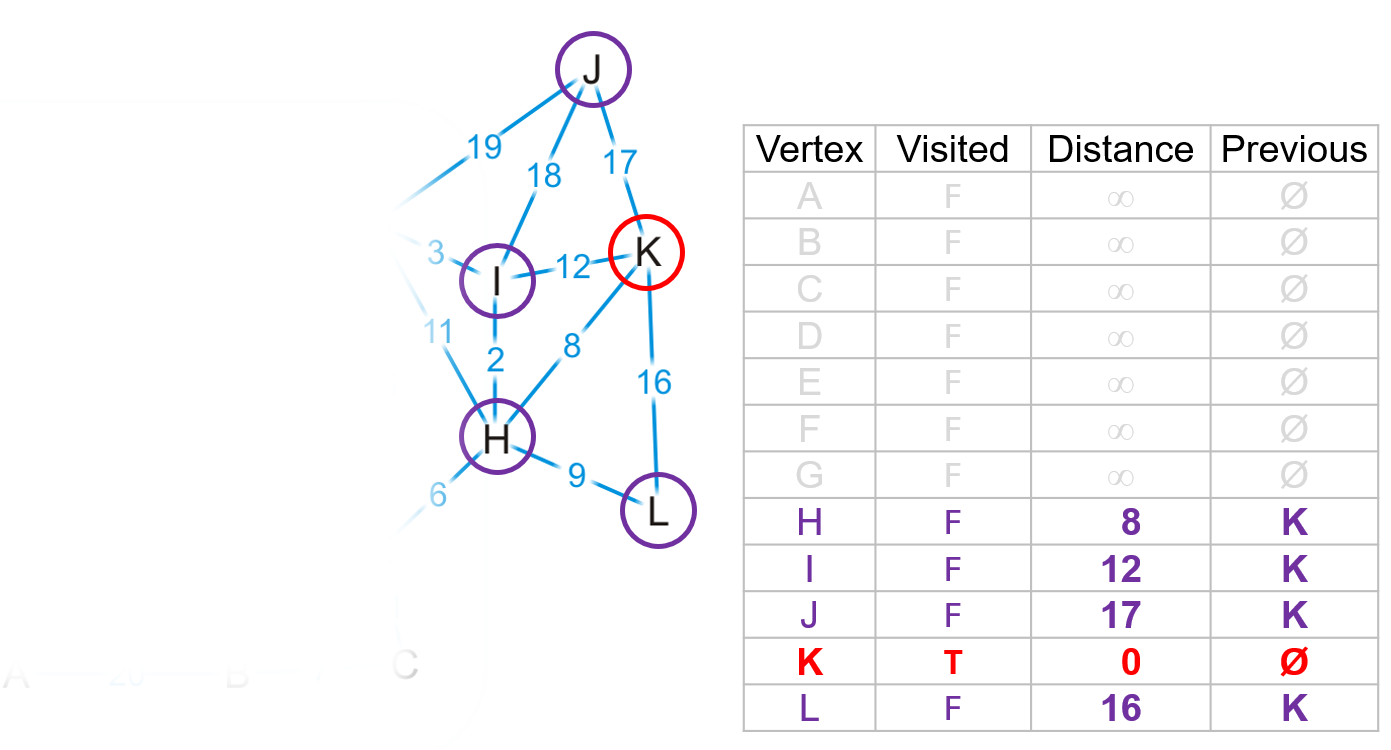
• 然后遍历$K$的所有邻接顶点，更新最短路径距离与前驱顶点指针
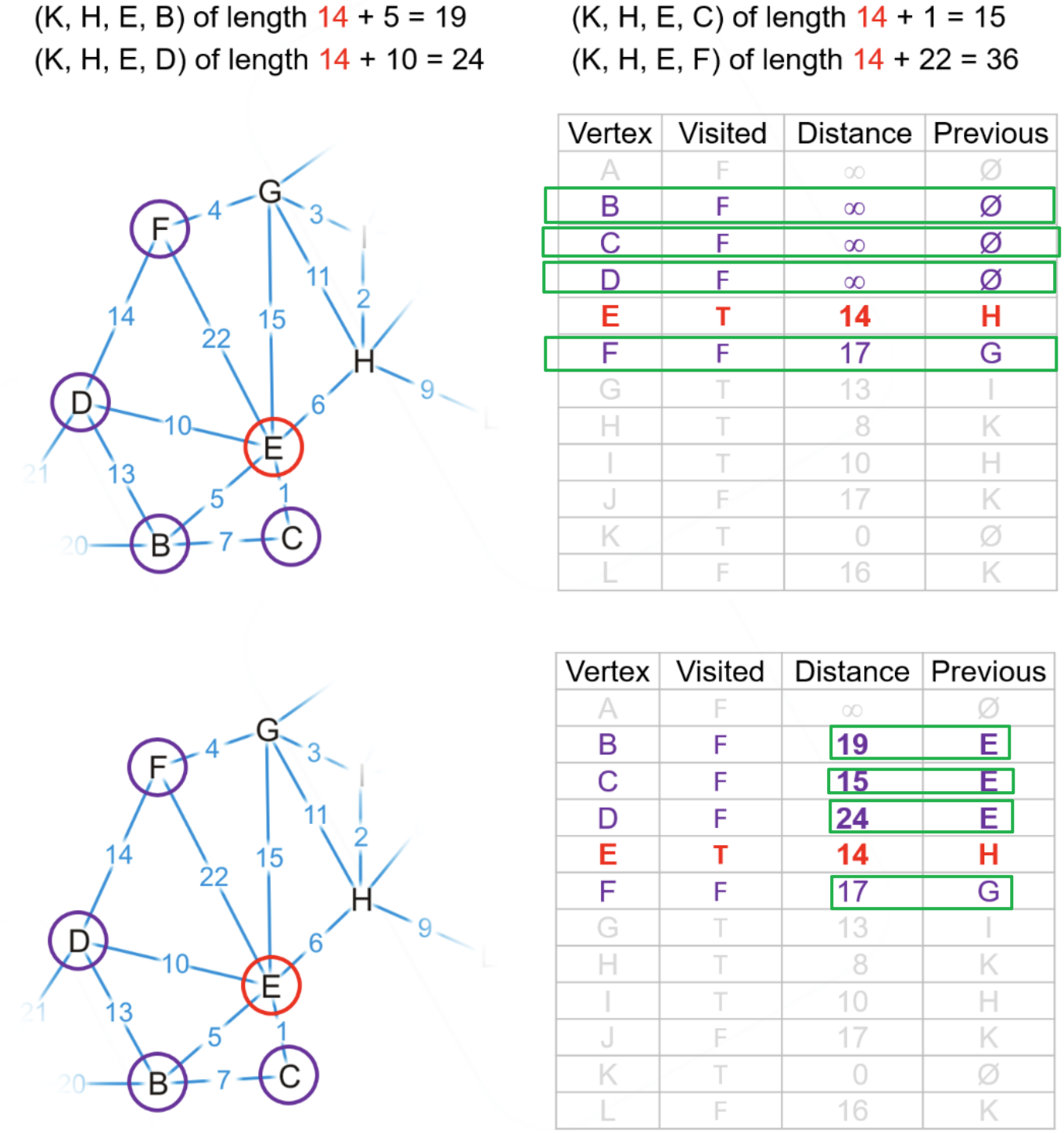
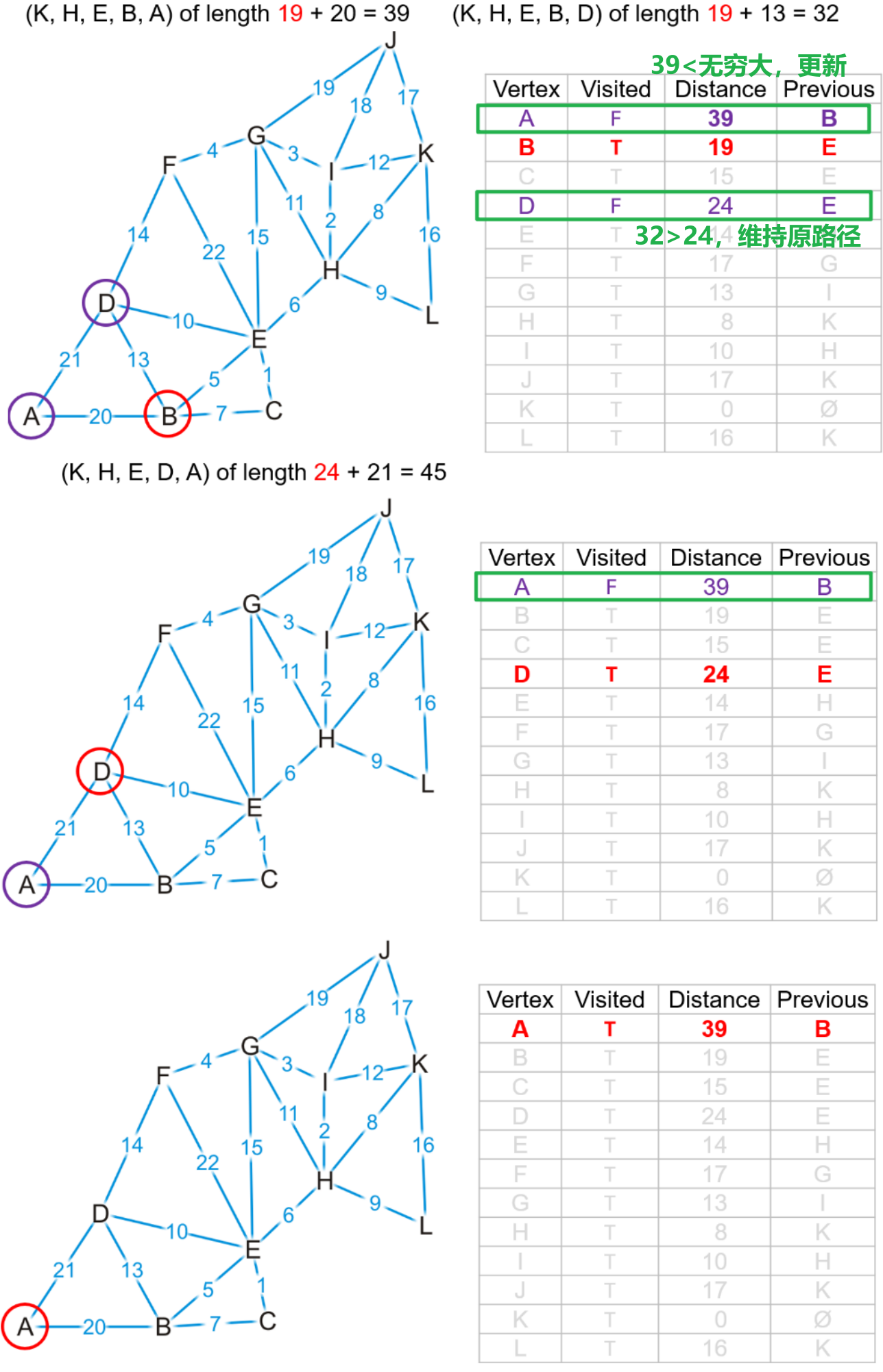
  • 此时我们可以确定到$H$顶点的最短路径必定是$(K,H)$，因为$H$点是$K$的所有邻接顶点中与$K$距离最小的一个，从$K$出发走任何其他路径的总长度必然大于走$(K,H)$
  • 反之对于其余的邻接顶点，例如$J$，我们暂时无法确定整个图中是否存在像$(K,H,…,J)$的一条路径，使得其总长度小于$(K,J)$的边长度
  • 所以对于$K$的所有邻接顶点，只有$H$的bool能被更新为true，其余都只需更新距离和前驱

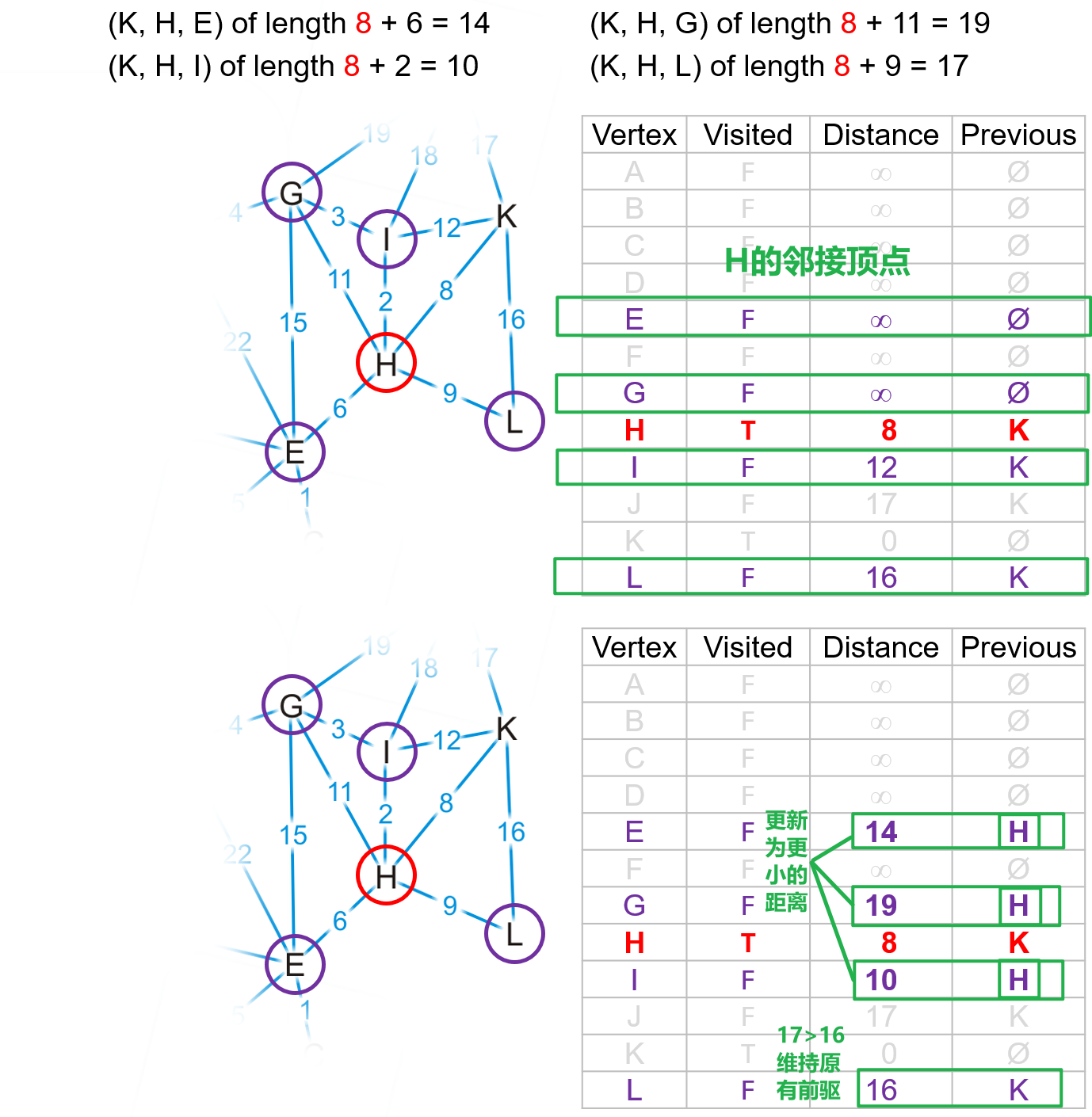
• 我们以$(K,H)$作为从$K$到其余顶点的最短路径中的起始部分，然后继续从$H$点开始找到$H$的共四个邻接顶点，我们发现对于列表中bool为false的顶点
  • $(K,H,E)$路径的长度$14<\infty$（列表距离项的初始值），所以需要更新$E$点的距离为$14$以及其前驱顶点为$H$，路径$(K,H,G)$和$(K,H,I)$同理，更新$G$和$I$点
  • 而$(K,H,L)$路径的长度$17>16$，所以维持原有的路径$(K,L)$即可

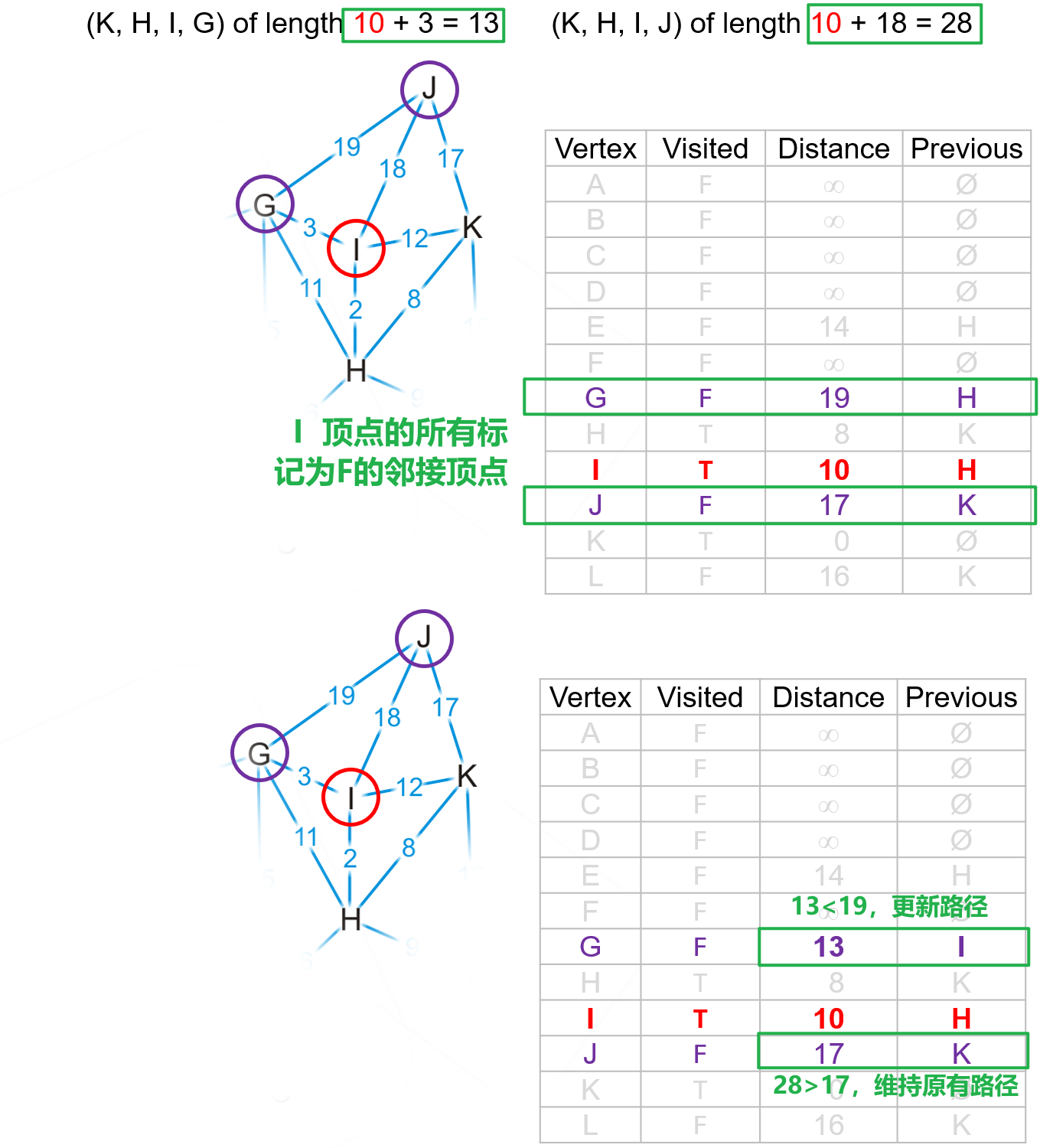
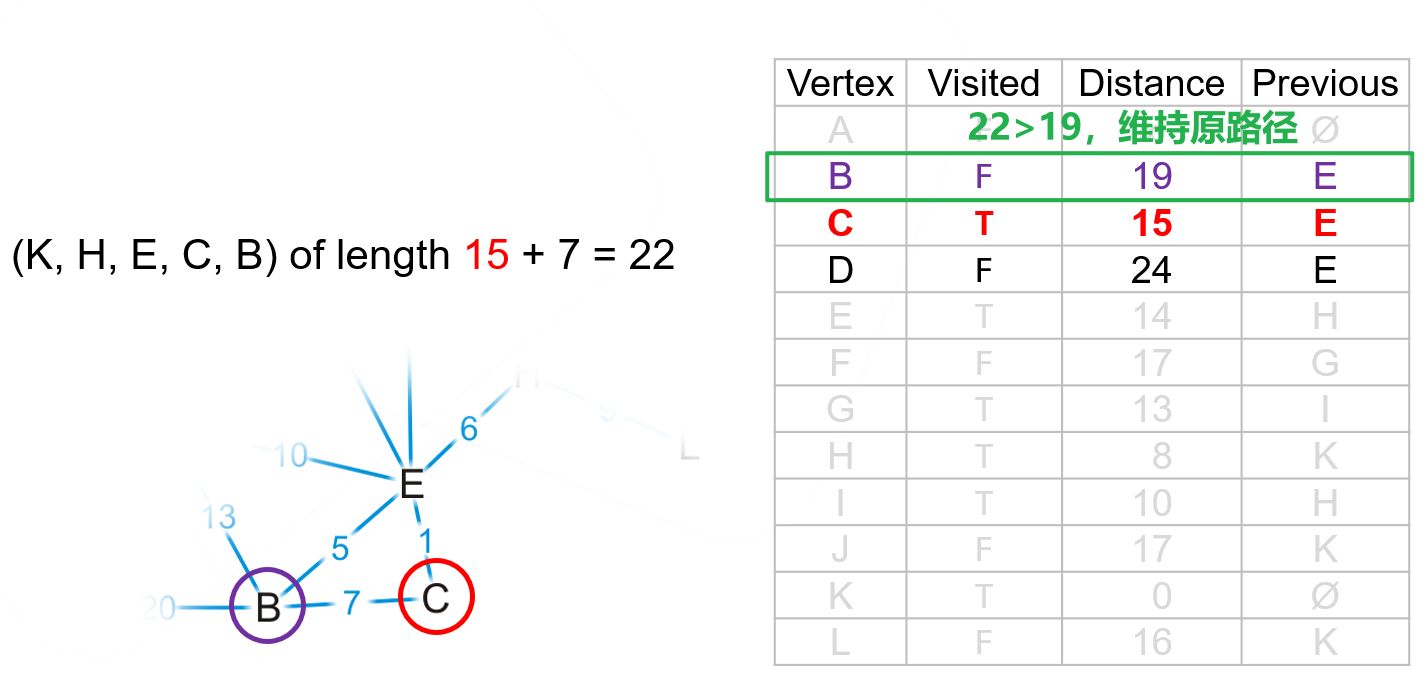
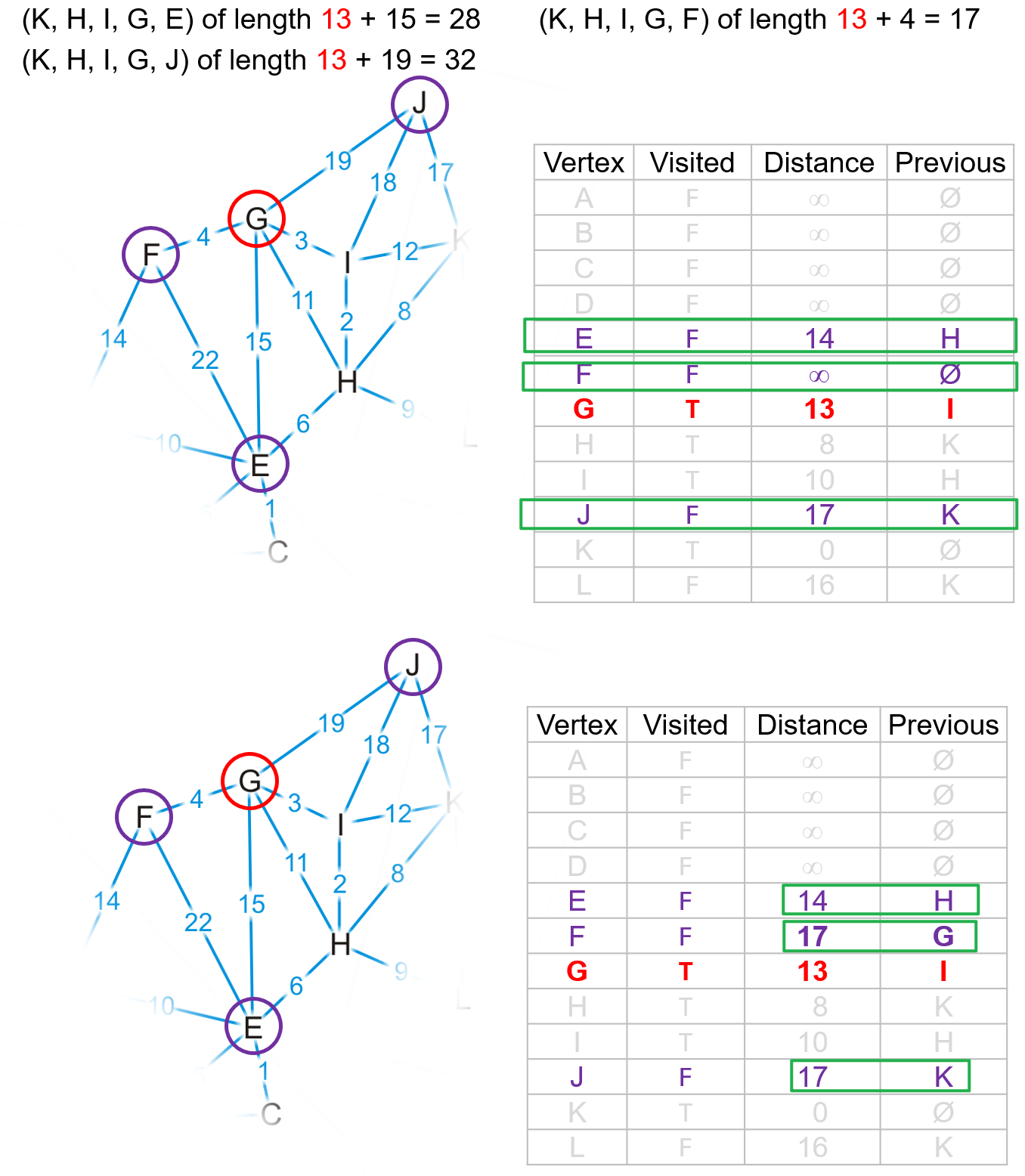
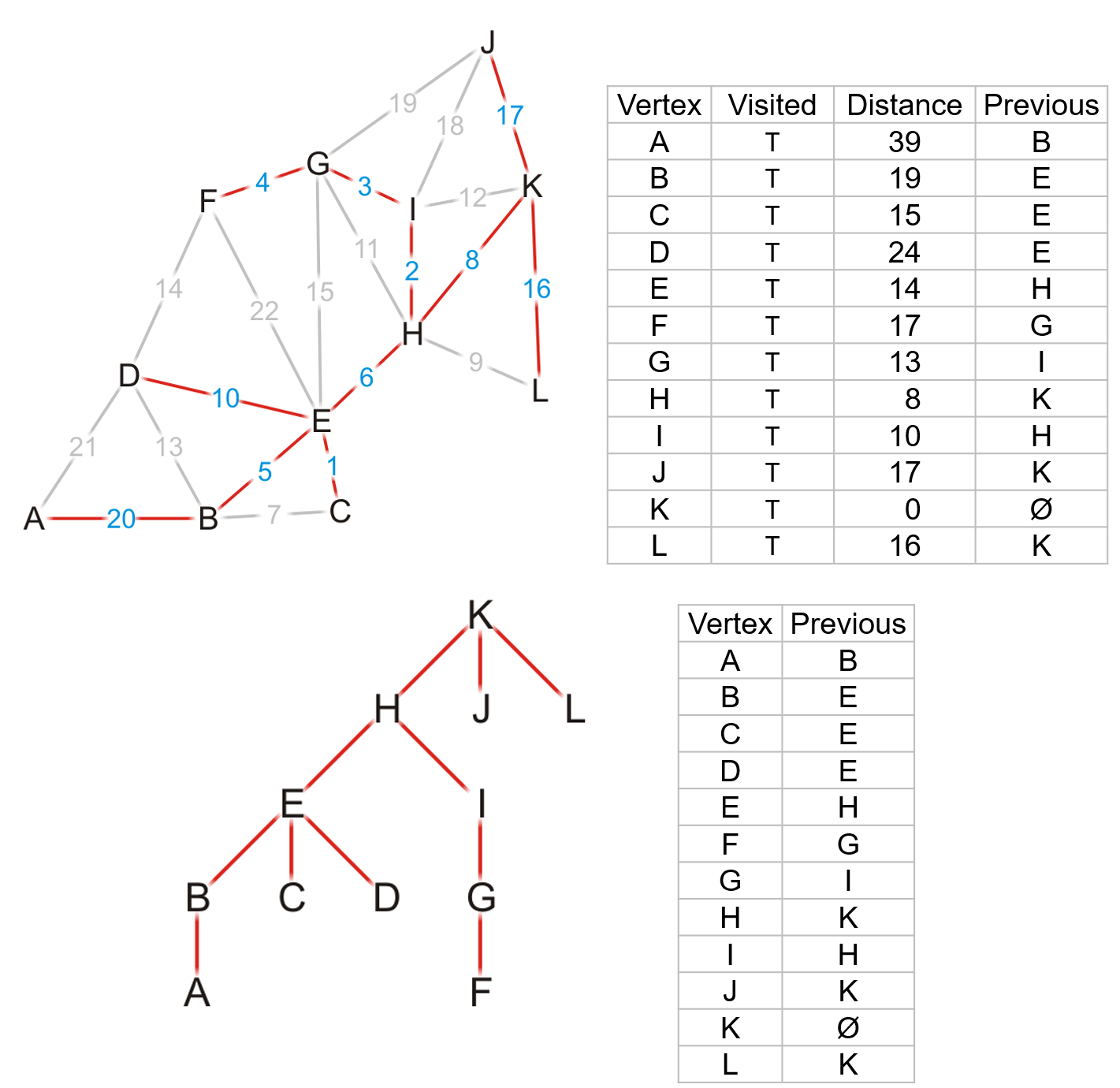
• 更新完$H$的所有邻接顶点后，我们并未产生新的true的顶点，故遍历整个列表中的false顶点并找出距离项最小的顶点作为下一个被检查的顶点，此处为$I$点，将其标记为true然后找到其邻接顶点（只需找到false的顶点，无需关心true的）进行更新即可

• 然后重复上述步骤，找到false的顶点中现有路径长度最小的，标记为true继续更新

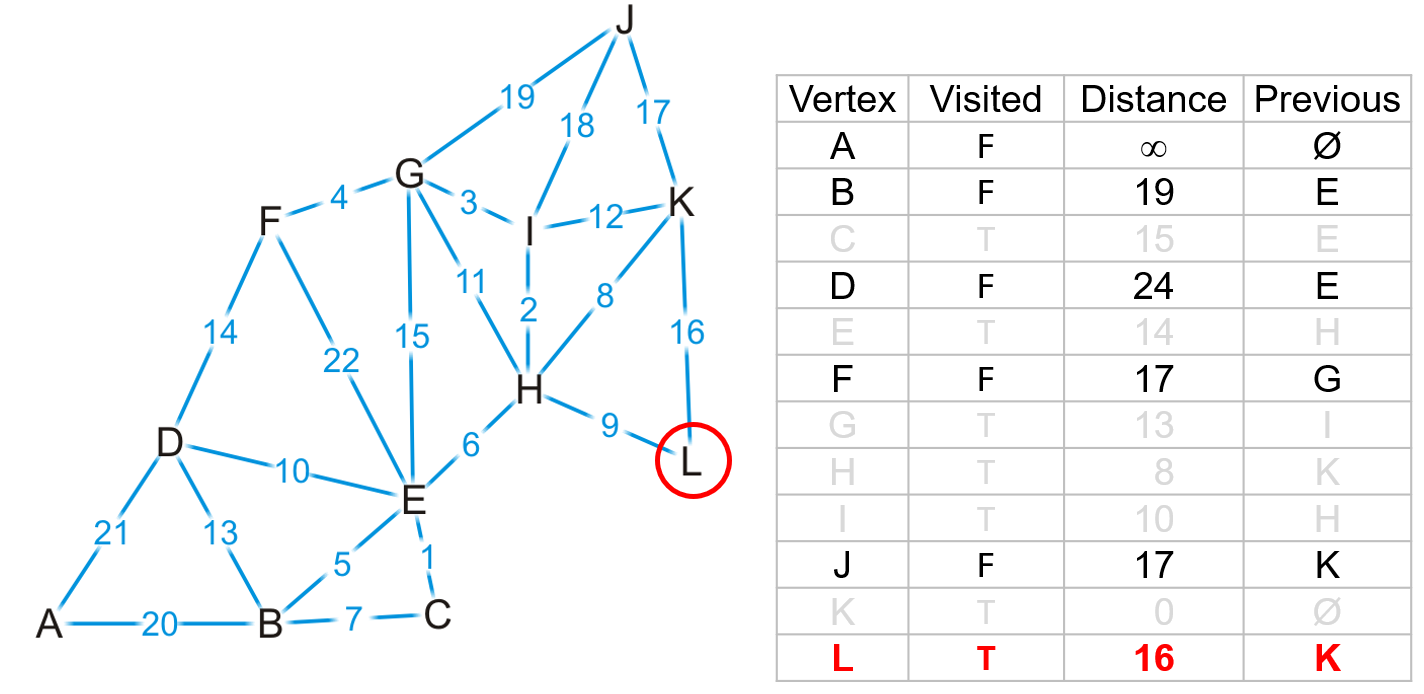
• 在这个过程中，我们遇到了邻接顶点全为true的顶点$L$，说明该顶点此时的路径已经是最短的

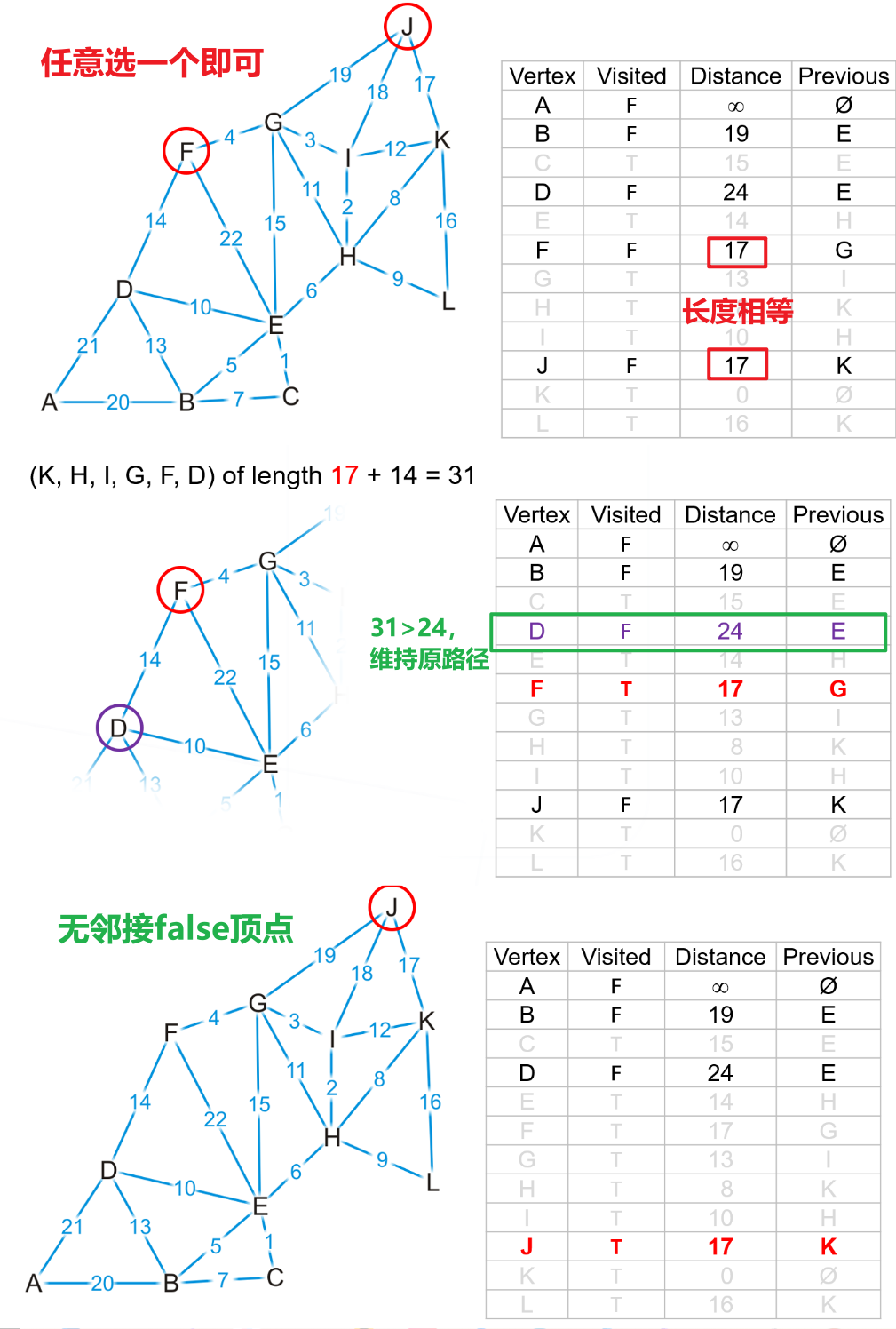
• 我们又遇到了已有false顶点中路径最小且相等的两个顶点，任意选一个作为下一个即可

• 然后继续检查，直到所有顶点都是true为止

• 最后我们就找到了这个加权图中，从$K$作为起点，到所有其它顶点的最短路径

• 如果在算法执行过程中发现所有false的顶点的已有路径距离均为$\infty$且前驱顶点为nullptr，则说明该图不是连通的，此时我们只找到了包含初始顶点在内的子图中所有顶点（即列表中被标记为true的所有顶点）到起始顶点的最小路径
• 如果我们只需要找到$v_i$和$v_j$之间的最小路径，那么我们只需选取其中一个作为起点，执行该算法直到检查到另一个顶点被标记为true即可停止

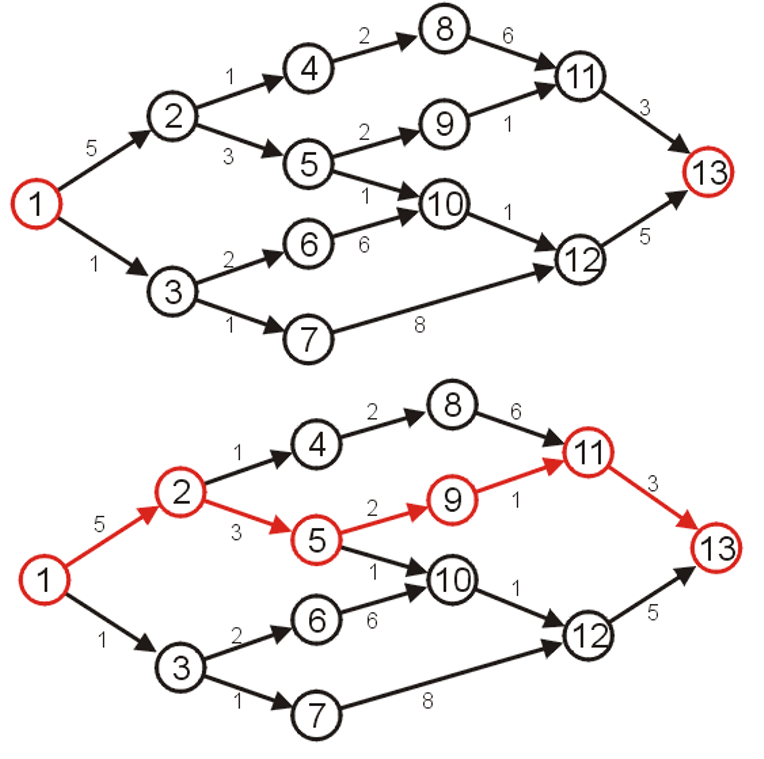
2.2 对比Prim算法

• Prim算法是寻找MST的算法，参考我的这篇博客：最小生成树之Prim与Kruskal算法
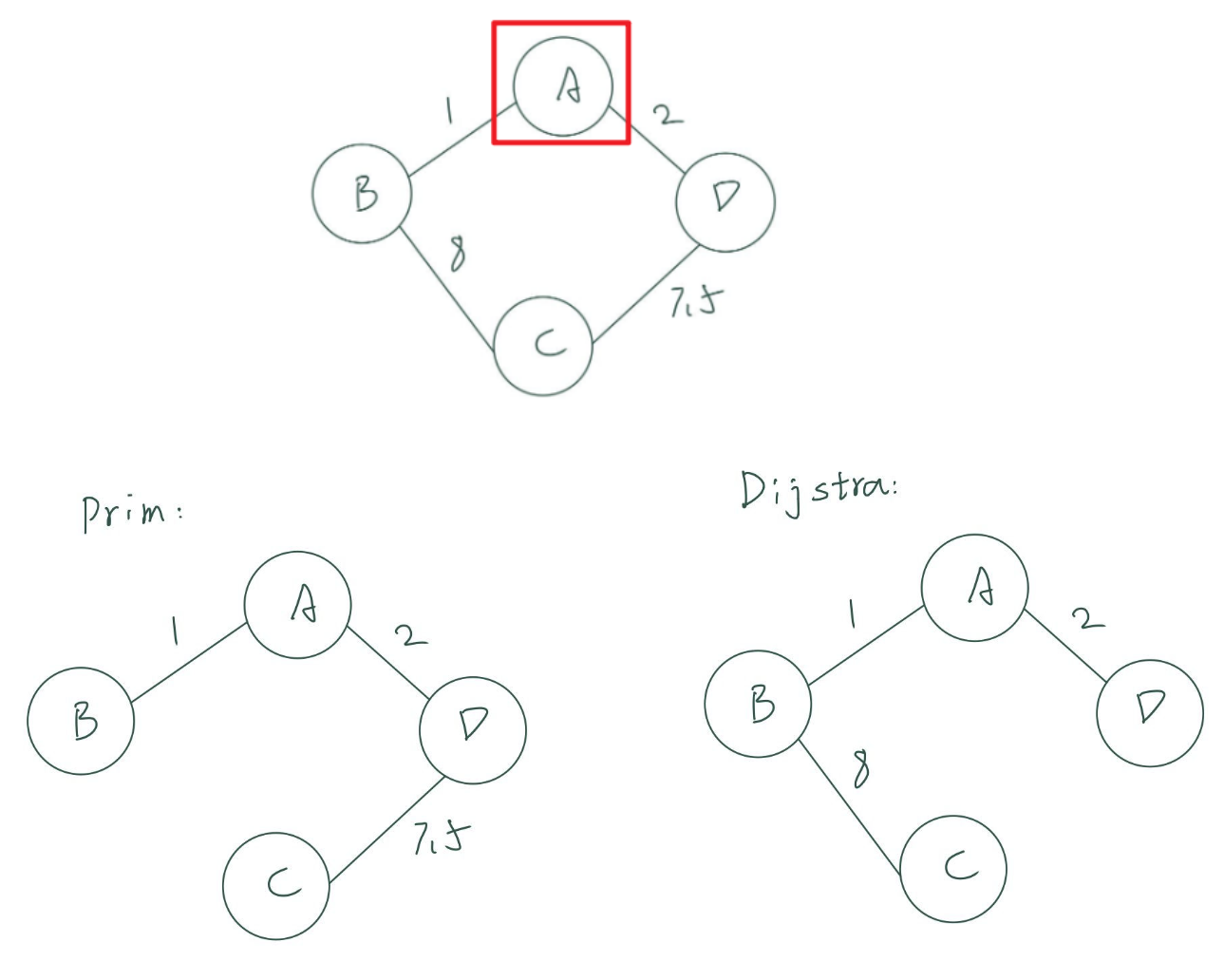
• 我们发现Dijkstra算法的实现过程和Prim很相似，但二者并非等价
  • Dijkstra算法并不能保证其找到的所有最小路径组成的生成树是最小权的，因为其在遍历过程中只关注从起点到终点的路径权，而没有关注整体的权，这是不同于Prim算法的
  • 反之Prim算法也并不能保证MST中的任意两个点之间的路径一定是原图中最小的
• 如下所示以$A$顶点作为起始点，经两种算法遍历后得到的生成树并不相同

2.3 算法分析与堆优化

• 选取起点后，初始化算法列表需要$O(|V|)$的空间和时间，然后算法需要进行共$(|V|-1)$轮，计算时渐进复杂度时直接使用$|V|$无妨，对于每轮算法：
  • 选目标：每轮需要先从false的顶点中找到其路径距离最小的那个，以确定此轮算法中被检查的顶点，这需要$O(|V|)$的时间复杂度（注意找出最小值并不是排序），所以算法整体用于该操作共需要$O(|V|^2)$的时间复杂度
  • 寻邻居：每轮算法都遍历所有的$(|V|-1)$个false的顶点，以找出当前被检查顶点的所有邻接顶点，这对于邻接矩阵需要$O(|V|^2)$时间，对于邻接列表需要$O(|E|)$的时间
  • 所以该算法的总时间复杂度为
    • 对于邻接矩阵实现：$O(|V|^2+|V|^2)=O(|V|^2)$
    • 对于邻接列表实现：$O(|V|^2+|E|)=O(|V|^2)$
• 由于该算法和Prim算法相似，所以我们可以采取同样的堆优化思路来优化算法过程中寻找路径最小的顶点这一步骤的时间复杂度，同时最好使用邻接列表实现的图以实现最优时间效率，下面我们以二叉最小堆为例，其插入、查找、删除节点的时间复杂度均为$O(\ln{n})$
  • 插入：初始化堆或优先队列需要将起点的邻接顶点推送（$O(\ln{|V|})$）入堆中，后续每轮都可能需要新增节点（$O(\ln{|V|})$）到堆中，新增的操作必然是总共$|V|$次，共需时间$O(|V|\cdot\ln{|V|})$
  • 取出：每轮操作需要取出堆顶顶点，共需要取$O(|V|)$次，总时间复杂度为$O(|V|\cdot\ln{|V|})$
  • 更新：每一轮中我们都需要遍历（$O(\ln{|V|})$）所有原有节点的距离值，并弹出（$O(\ln{|V|})$）被更新的节点，然后将其重新存入（$O(\ln{|V|})$）堆中，该操作需要重复边数$|E|$次
  • 所以二叉最小堆优化所需时间复杂度共$O((2|V|+|E|)\cdot\ln{|V|})=O((|V|+|E|)\cdot\ln{|V|})$
• 如果使用斐波那契堆进行优化，其插入操作的时间复杂度为$O(1)$，虽然其删除操作的时间复杂度仍为$O(\ln{n})$，但是我们只需将被更新了的节点移动到正确的位置，斐波那契堆执行该操作仅需时间复杂度$O(1)$
  • 插入：插入（$O(1)$）新节点共$|V|$次，所需时间复杂度共$O(|V|)$
  • 取出：共需取出$|V|$次，取出即删除（$O(\ln{|V|})$）堆顶节点，故共需$O(|V|\cdot\ln{|V|})$时间
  • 更新：更新（$O(1)$）原有节点共$|E|$次，所需时间复杂度共$O(|E|)$
  • 所以斐波那契堆优化所需时间复杂度共$O(|V|\cdot\ln{|V|}+|E|+|V|)=O(|V|\cdot\ln{|V|}+|E|)$