最小生成树之Prim与Kruskal算法

一、关于生成树

1.1 生成树的定义

• 对于一个$|V|=n$的连通的图，生成树（Spanning Tree）被定义为连通这所有$n$个顶点的$(n-1)$个边的集合，这$(n-1)$个边和$n$个顶点构成了原图的一个连通的子图
• 由于连通$n$个顶点的方式不一定唯一，所以一个连通图的生成树不一定唯一

• 由生成树的定义（连通所有顶点的$(n-1)$个边）可知，其对应的子图是满足$|E|=|V|-1$的，故而该子图应当是无环的，且可以被整理为树的结构形式（也可能是链表）

• 对于加权图的生成树，其权重等于其包含的边的总权重

1.2 生成森林的定义

• 对于那些不连通的图，其必然由$N$个连通的导出子图所构成，每个导出子图内包含的共$N$个生成树就一同构成了这个原图的生成森林（Spanning Forest）

1.3 二者的应用

• 对于一个需要被供电的电路、建筑群等，可以将所有需求电的单元看作是顶点，其间的有长有短的通路就是带权边，二者构成的加权无向图的最小权重的生成树就可以给出最低耗费的供电方案
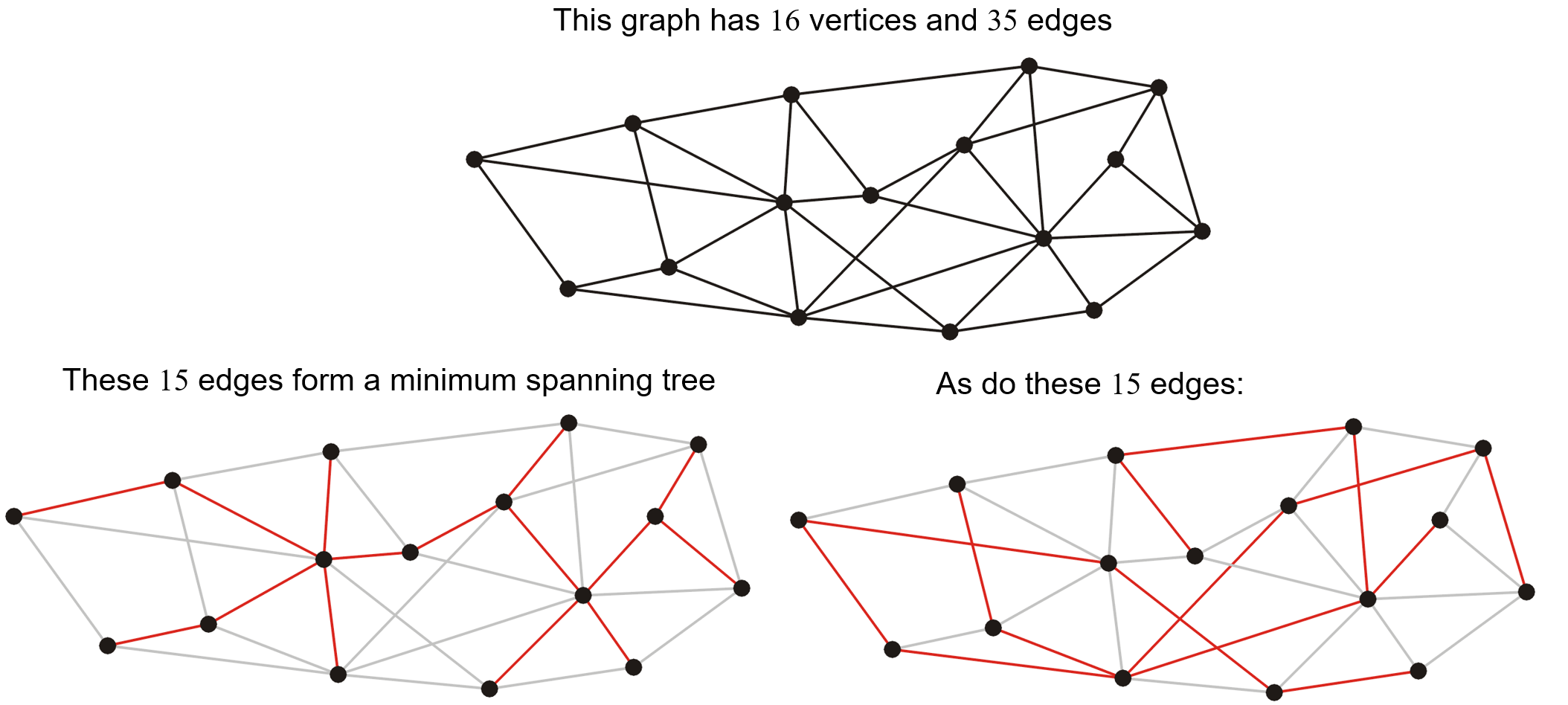
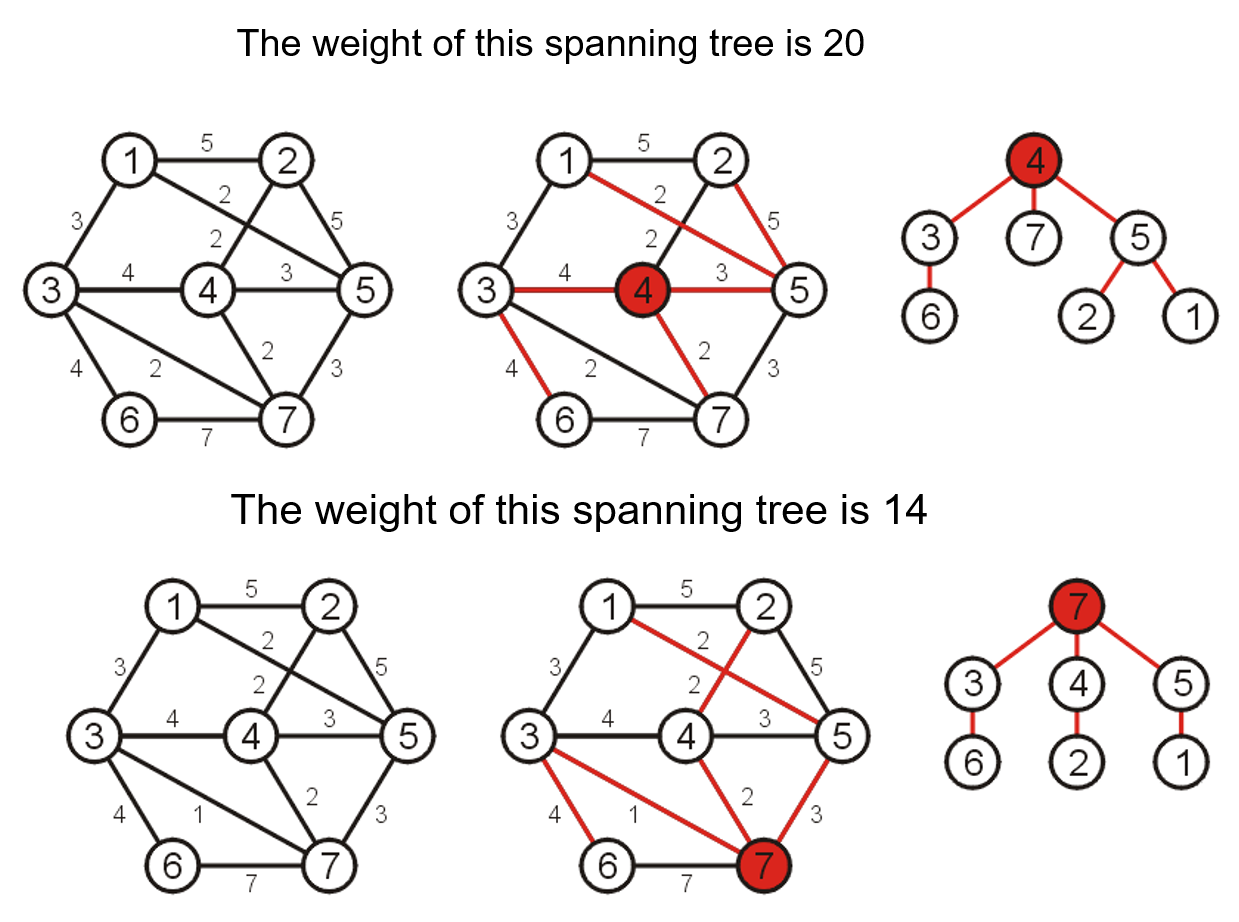
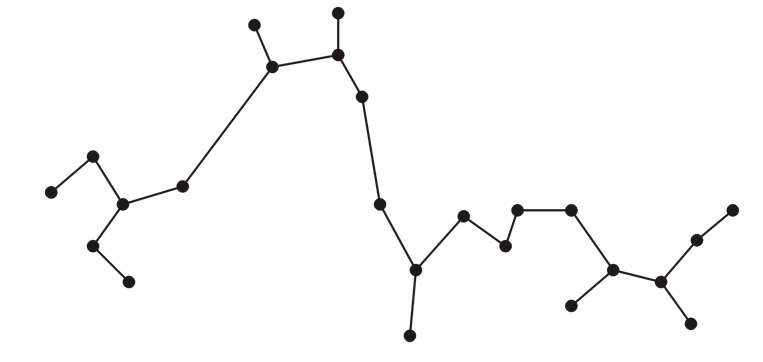
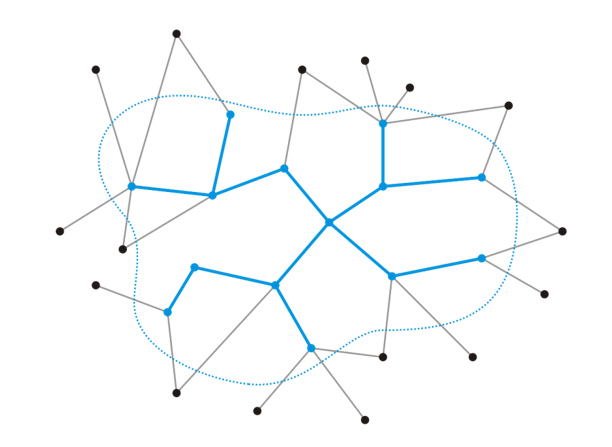
• 例如对于下图中的顶点（可以想象为信号基站、供电单位等具有实际意义的东西），假设任意两点间都可以连通，顶点间的距离就是权重

• 那么对于这个整体我们就能找到一个最小权重的生成树，如下图所示

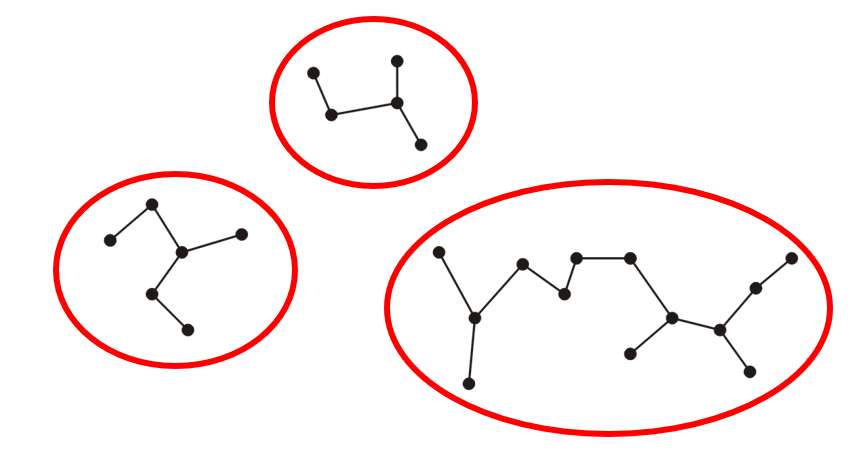
• 其中过长的边（权重过大）我们将其去掉，整体便被分为了三个更小更易于管理的子图，如此整体就变为了一个生成森林

• 如此我们便知晓了加权图中的最小权生成树（MST）的重要性，常用以下两个算法进行寻找
  • Prim’s Algorithm
  • Kruskal’s Algorithm

二、Prim算法

普立姆算法（Prim’s Algorithm）又称加点法

2.1 思路引入

• 试想我们已经知道了图中$n$个顶点中的一个包含$k\geq1$个顶点的MST，如何延伸这个MST到整个图上呢？我们需要将以外的$(n-k)$个顶点全部设法并到已有的MST上

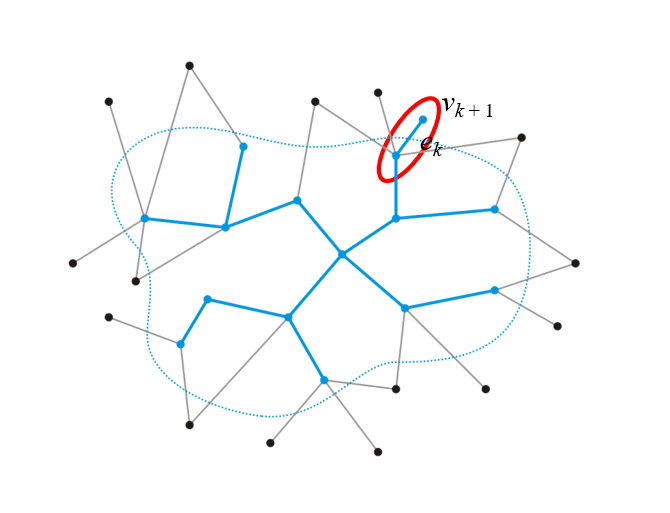
• 遍历还未被并入MST上的另外$(n-k)$个顶点，找到一个顶点（如下图的$v_{k+1}$），使得这个顶点与MST内的某个顶点间的边是所有能找到的连接MST内外的边中最短的一条，我们将这个边并入已有MST中即可，然后重复上述操作直到MST内的边数等于$(n-1)$即可
• 如果找不到任何一个连通MST内外点的边，那么整个图就不是连通的，无法化为单个生成树

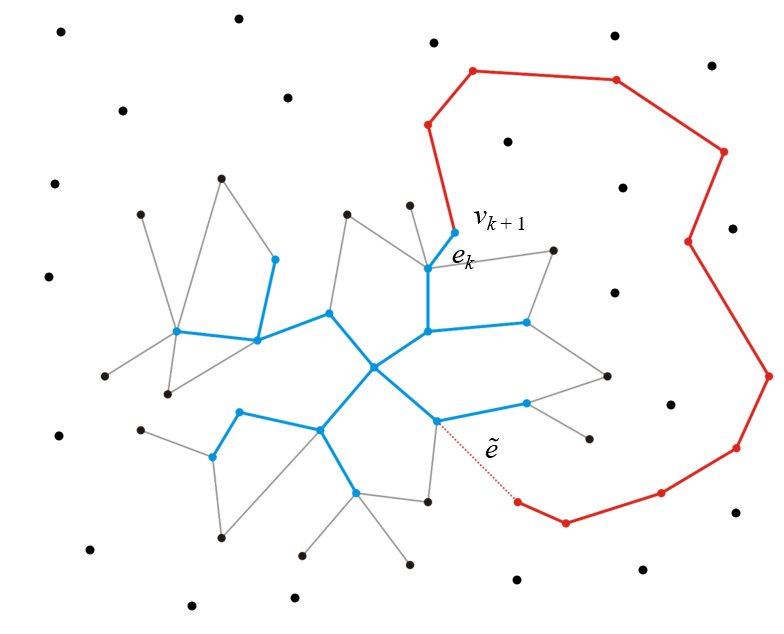
• 为何必然是找到单个边而不是多个边的路径？因为其他的任意一条包含多个树外$(n-k)$内顶点的路径都必然在路径末尾包含一条连通MST外某顶点与MST内某顶点的边（如下图的$\widetilde{e}$），而这个边的权重必然是大于我们已经找到的最短的边（如下图的$e_k$）的权重的（请回顾我们是如何找出这个最短边$e_k$的），更别说这整个路径还需要加上如下图红色部分的权重，路径总权重必然是大于已找到的边$e_k$的权重的

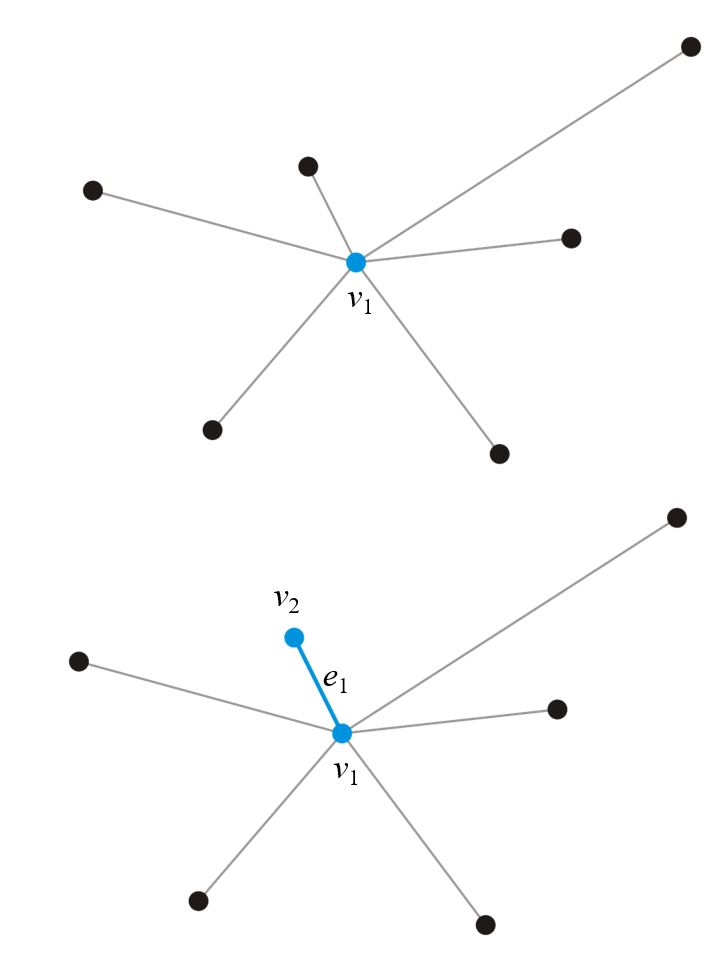
• 理解上述内容后，若想寻找一个连通的图的MST，则先任意选取一个顶点作为开始，将这个顶点视为$k=1$的初始MST，遍历树外其它点找出最短的边，应用上述思路即可

2.2 具体实现

• 为了实现该算法，我们需要维护以下三个长度均为$|V|$的数组（对应图中每个顶点）
  • 布尔值数组arr1：记录顶点是否被放入MST中
  • 浮点数数组arr2：记录该位置顶点距离MST内所有顶点的边中的最小边权
  • 整型数数组arr3：记录树内的距离该位置顶点的边权最小的顶点的索引
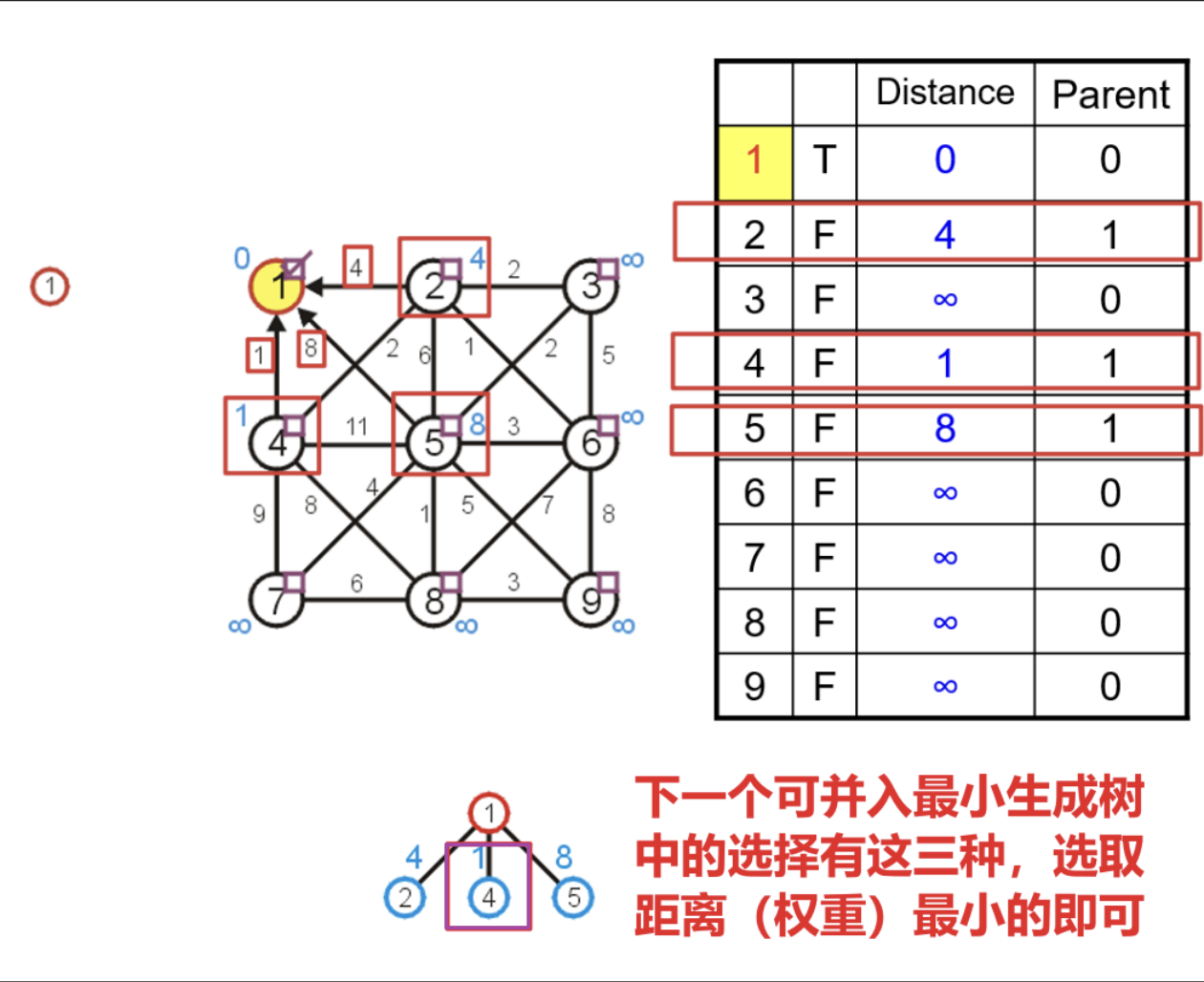
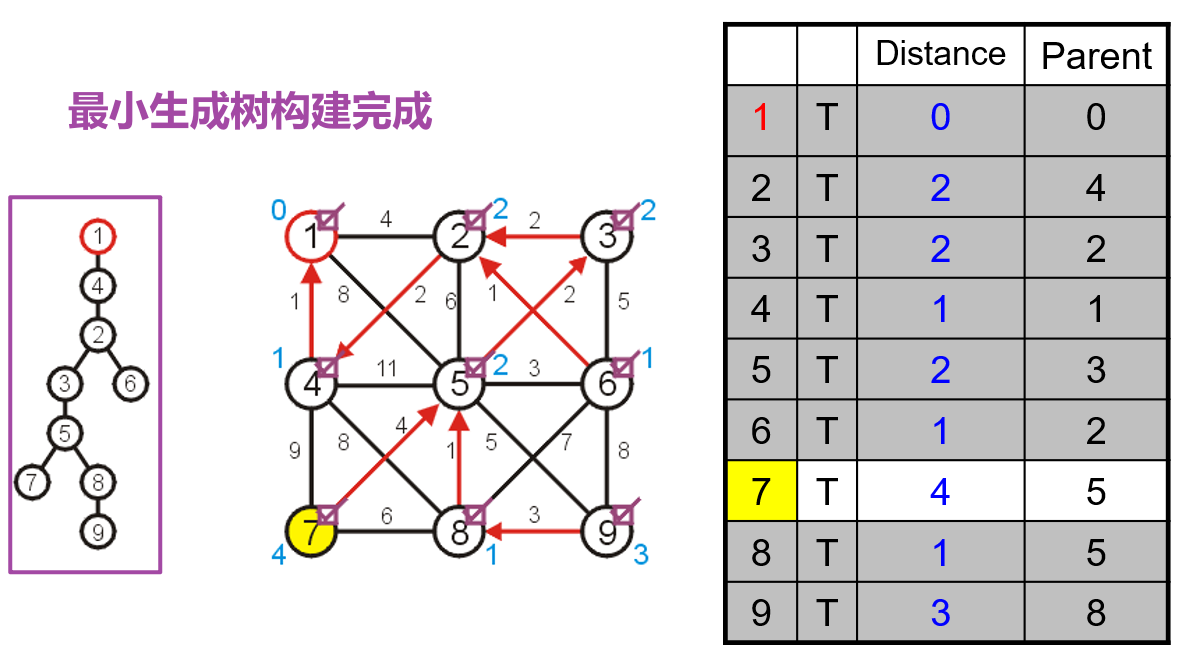
• 在最开始时，需要进行如下操作
  • 任意选取一个顶点将其arr1中的对应位置设置为true，将其arr2中的对应位置设为0，将arr3中的对应位置设为无意义的某个索引（下图中的列表大概是空出了0索引处）
  • 除了选中顶点外的所有顶点也需要被初始化，如下图中将距离设为无穷

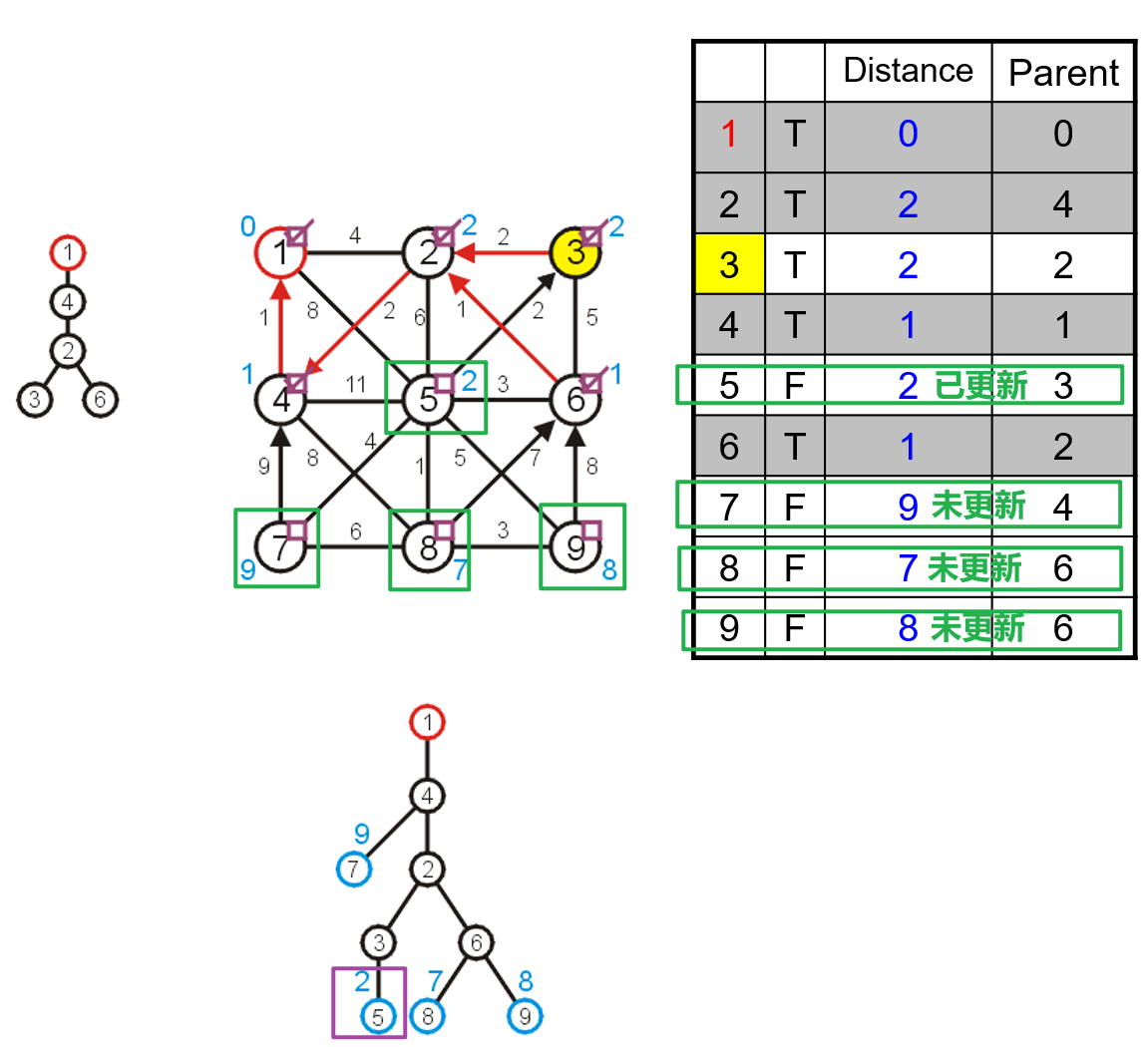
• 然后遍历与被选中顶点的所有邻接顶点，更新这些顶点在三个数组中的对应数据，找到这些临界顶点中距离最小生成树中唯一一个顶点间边长距离最短的一个，将其并入最小生成树中，并更新该顶点的布尔数组位置为true，并将其父节点索引更新

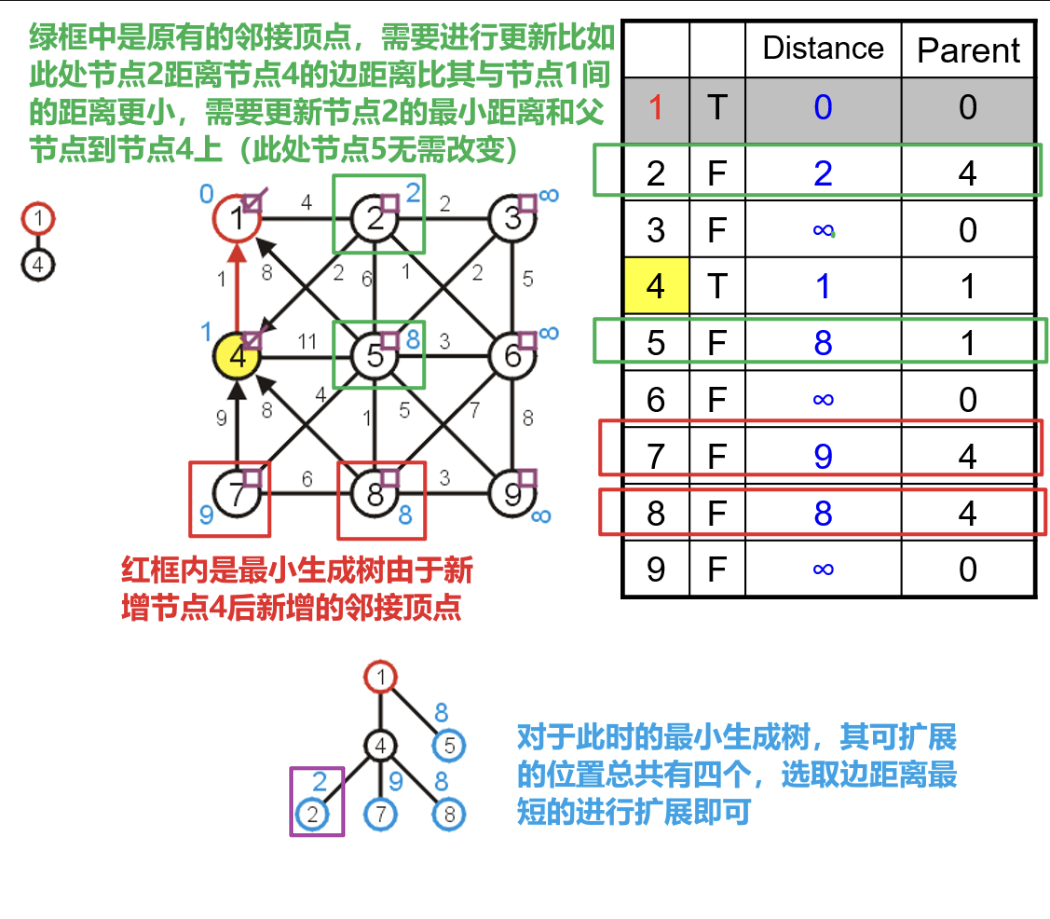
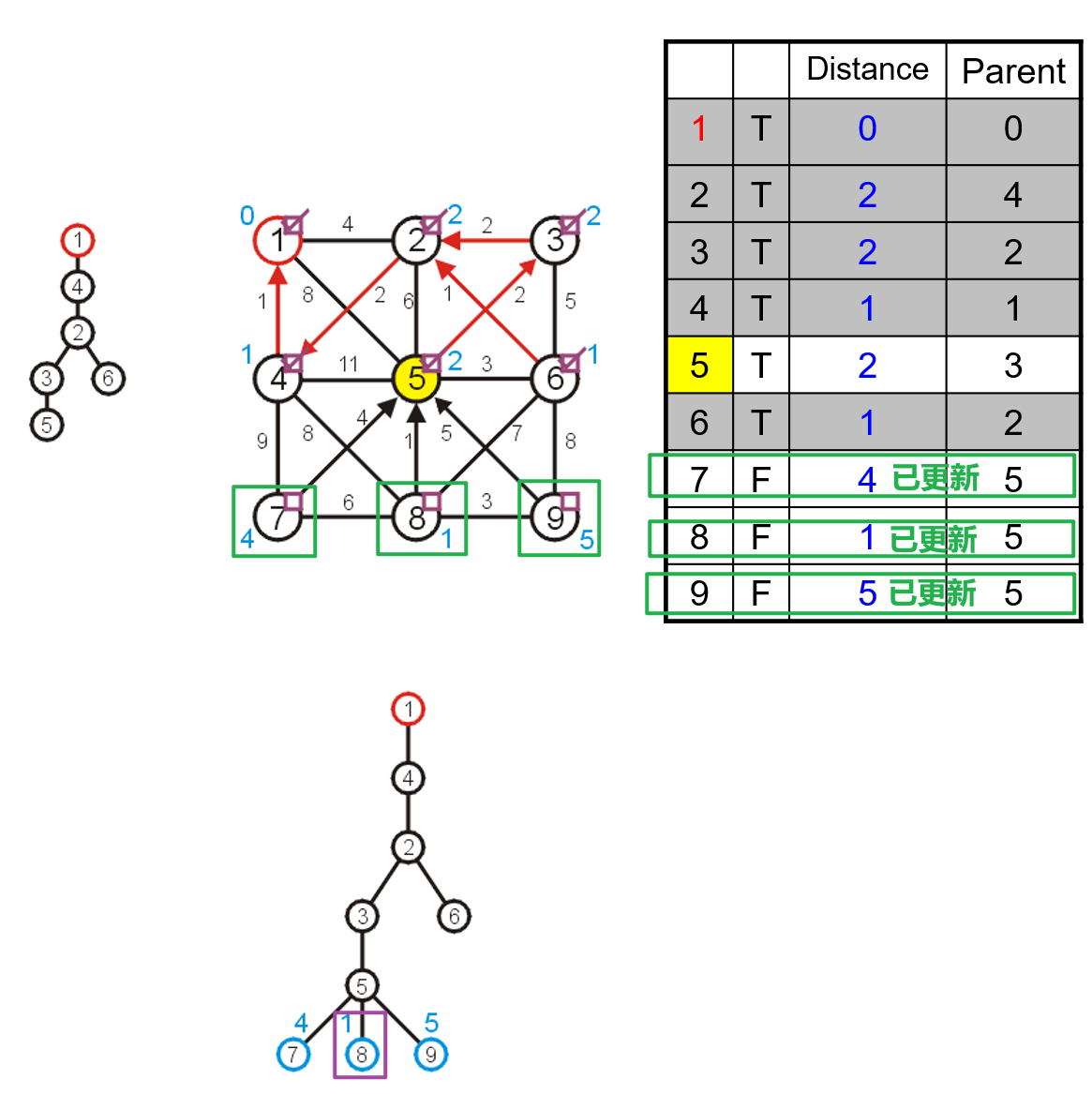
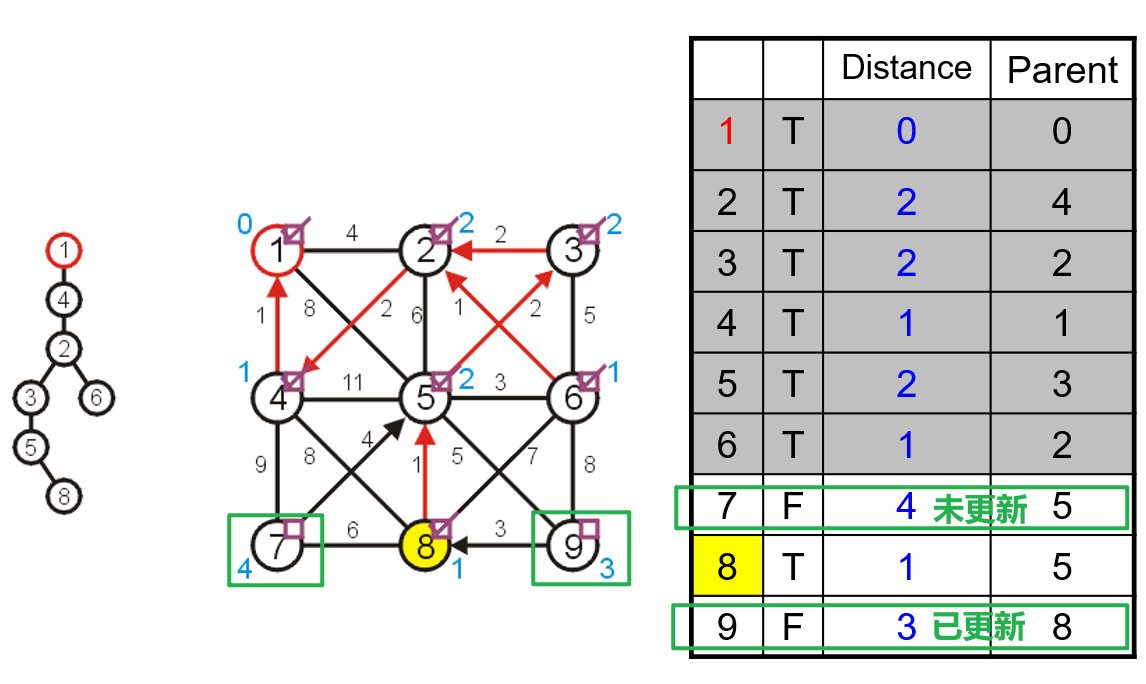
• 由于最小生成树中并入了新的顶点，所以首先需要找到新增的邻接顶点将其对应在三个数组中的数据更新，然后对于原有的几个邻接顶点，也需要依据其与新顶点间的距离而更新数据

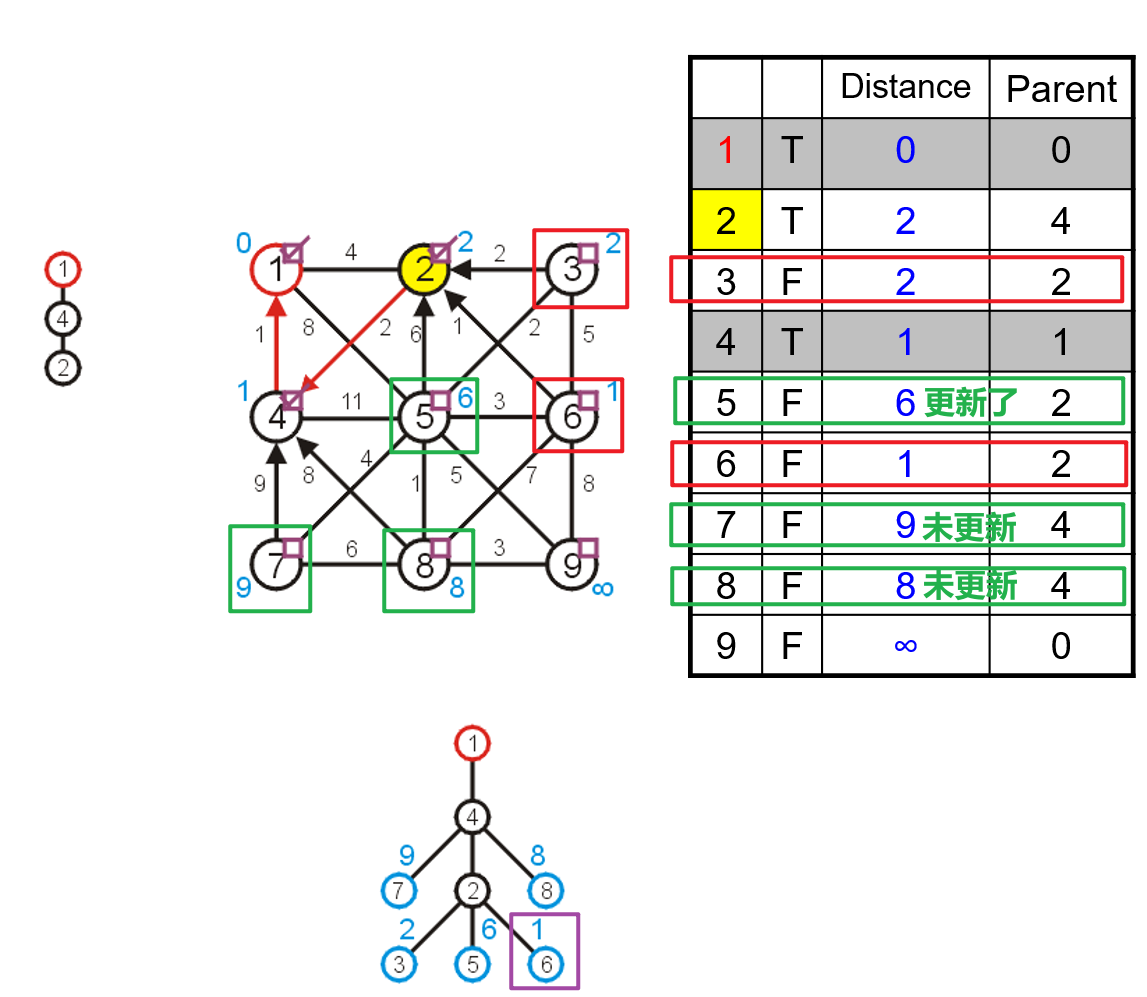
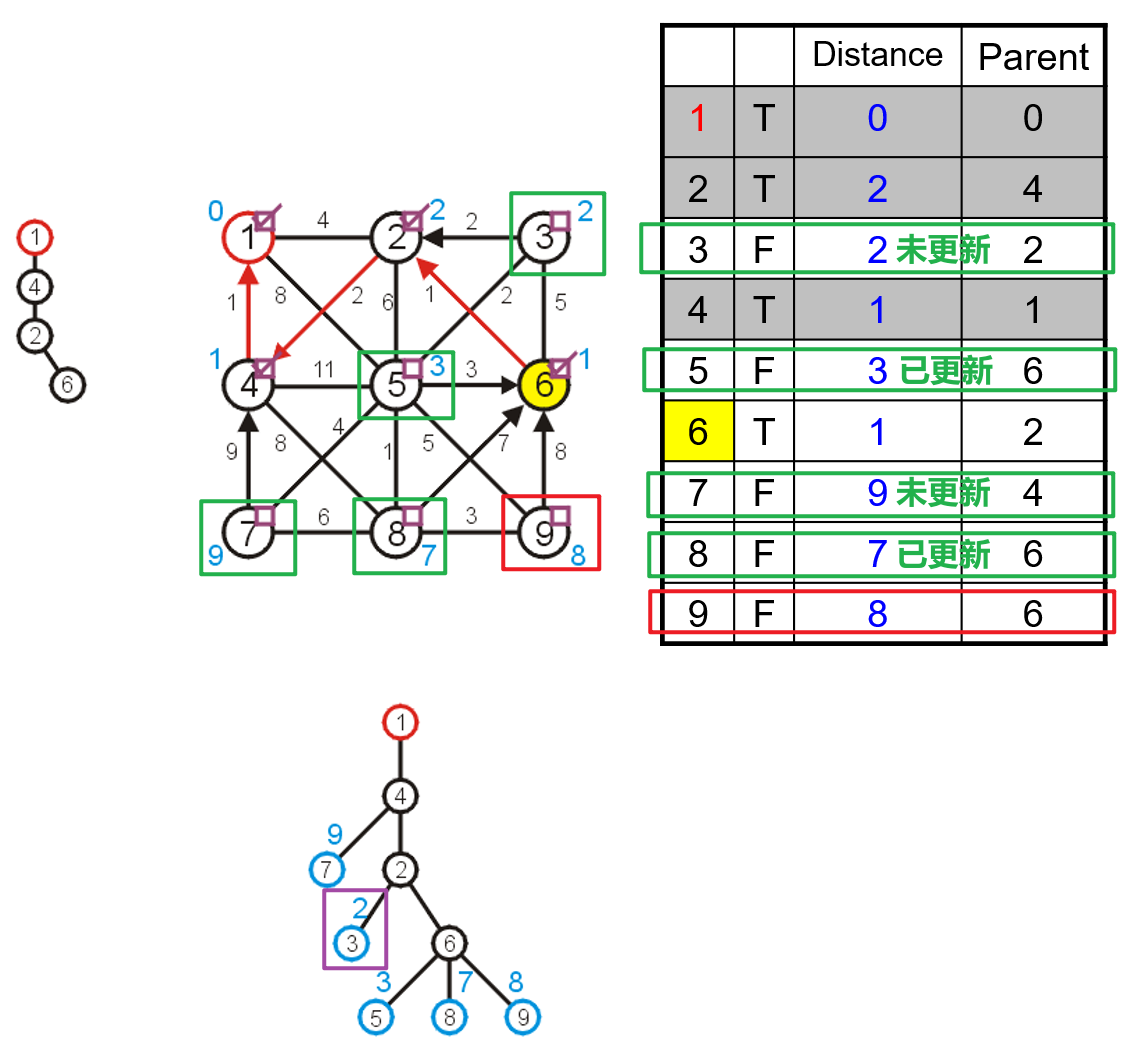
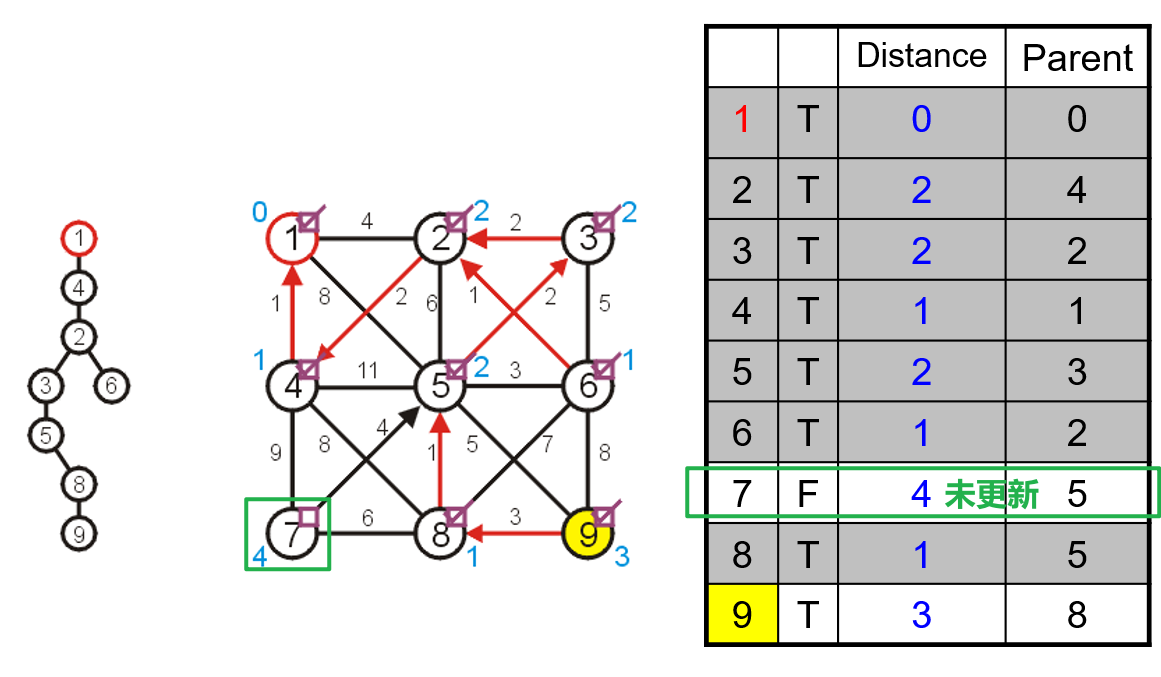
• 然后重复上述思路直到布尔值数组中的所有元素均为true即可，此时说明所有顶点均被纳入了最小生成树中

• 在上述过程中如果出现了所有false的顶点的距离均为$\infty$的情况，说明这个图并非连通的，此时所有true的顶点和边构成了原图的一个导出子图的最小生成树

2.3 算法分析

• 上述朴素算法实现需要$O(|V|)$的空间复杂度来存放三个数组
• 总体上我们需要遍历$(|V|-1)$轮，每一轮的任务就是找到距离最小生成树最短的边，每一轮中都需要遍历三个数组中false的顶点的信息以更新其距离和父节点状态，对于邻接列表实现，时间复杂度为$O(|V|^2+|E|)$，对于稠密图来说$|E|=O(|V|^2)$，此时$O(|V|^2+|E|)=O(|V|^2)$

2.4 堆优化

• 上述的朴素实现可以看作是使用了长度为$|V|$的std::vector<std::tuple<bool,float,size_t>>列表，其中最重要的其实是三元组中的float元素，因为每轮寻找仅需找到最小权的边即可，而无需暴力遍历所有的顶点，可以使用堆结构来优化该过程，此处以二叉堆中的最小堆为例
  • 插入：MST每轮需要将新的邻接顶点存入起始为空的堆中（按边权进行大小比较），由于堆的最大顶点数为$|V|$，故单个顶点的渗流时间复杂度视为$O(\ln|V|)$，由于所有顶点都必然要被加入进该堆中至少一次，所以时间复杂度总共为$O(|V|\cdot\ln|V|)$
  • 取出：每轮都需要取出堆顶的最小值节点，共需取$|V|$次，由于二叉堆的节点删除的复杂度尾$O(\ln{n})$，故时间复杂度共$O(|V|\cdot\ln{|V|})$
  • 更新：由于每次新增邻接顶点时，堆中原有的顶点若是与新增到MST中的顶点存在单条边的路径连通关系，则需要将该顶点从堆中弹出并重新以新的边权放入堆中，这需$O(\ln|V|)$的时间复杂度，该操作最多发生图中的总边数$|E|$次，故时间复杂度共$O(|E|\cdot\ln|V|)$
  • 所以二叉最小堆优化后的算法时间复杂度共为$O((2|V|+|E|)\cdot\ln|V|)$，由于$|E|\leq|V|^2$，而在稠密图中$|E|$十分接近于$|V|^2$，所以此情况下的时间复杂度为$O(|E|\cdot\ln|V|)$
• 此外还可以使用斐波那契堆进行优化，但斐波那契堆的空间占用实际上来说会相对更大
  • 插入：$O(|V|)$
  • 取出：$O(|V|\cdot\ln{|V|})$
  • 更新：$O(|E|)$
  • 所以二叉最小堆优化后的算法时间复杂度共为$O(|V|\cdot\ln|V| + |E|)$

2.5 代码实现

• 待补充

三、Kruskal算法

克鲁斯卡尔算法（Kruskal’s Algorithm）又称加边法

3.1 思路引入

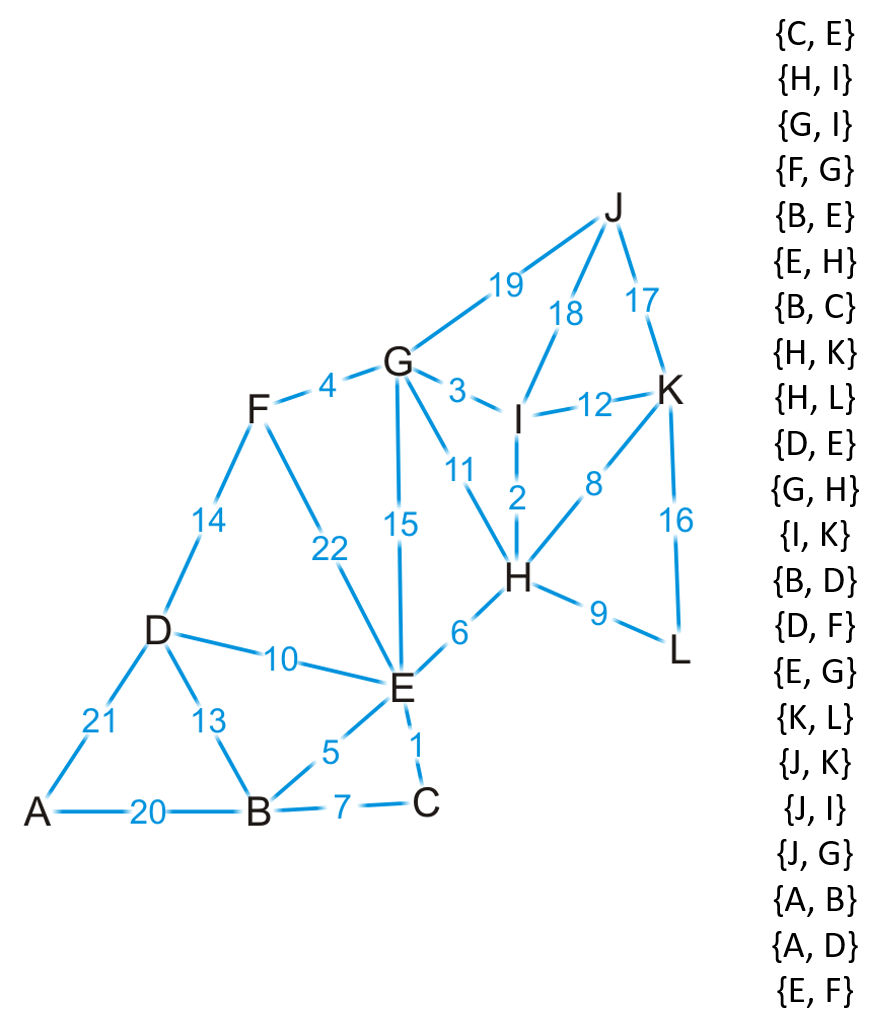
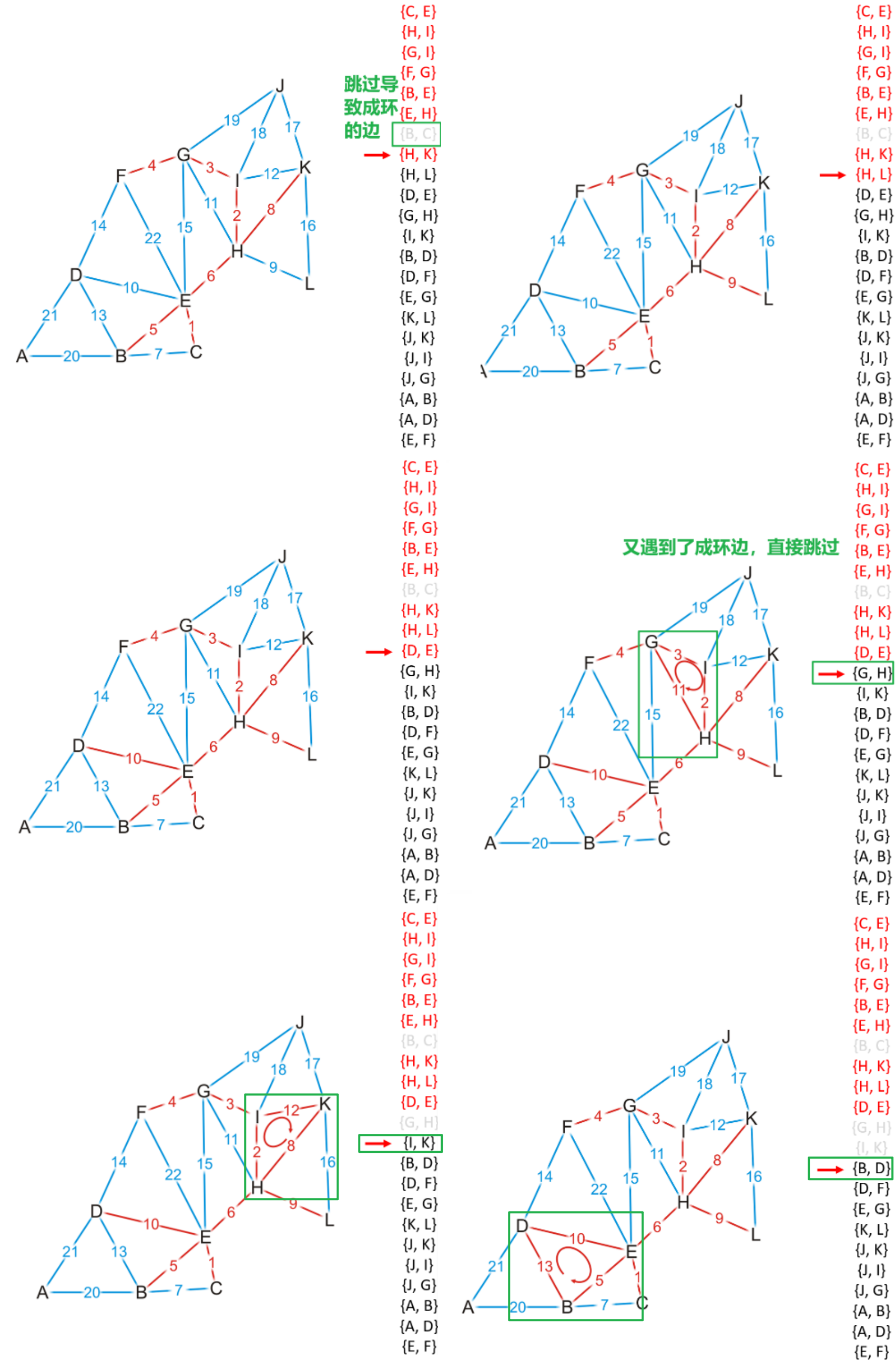
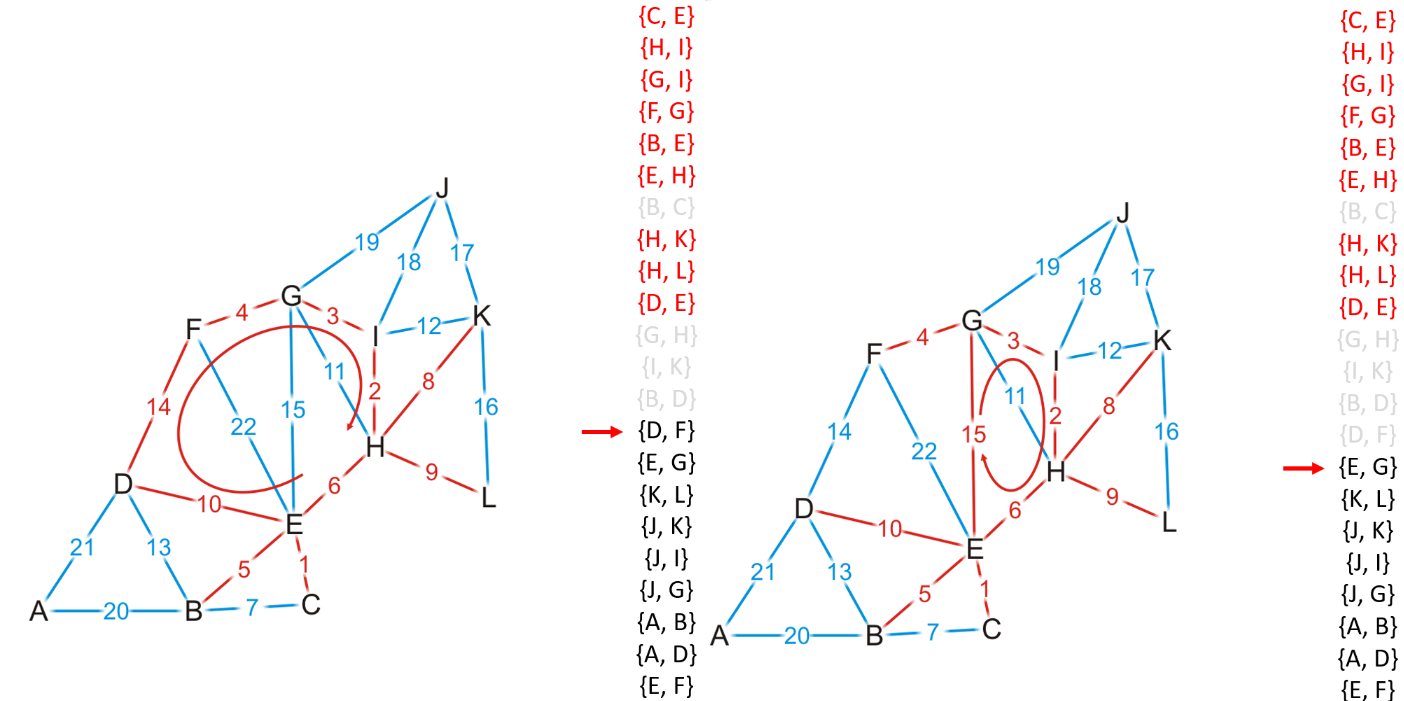
• Kruskal算法在开始时将图中的所有边按权重从小到大进行排序，如下图

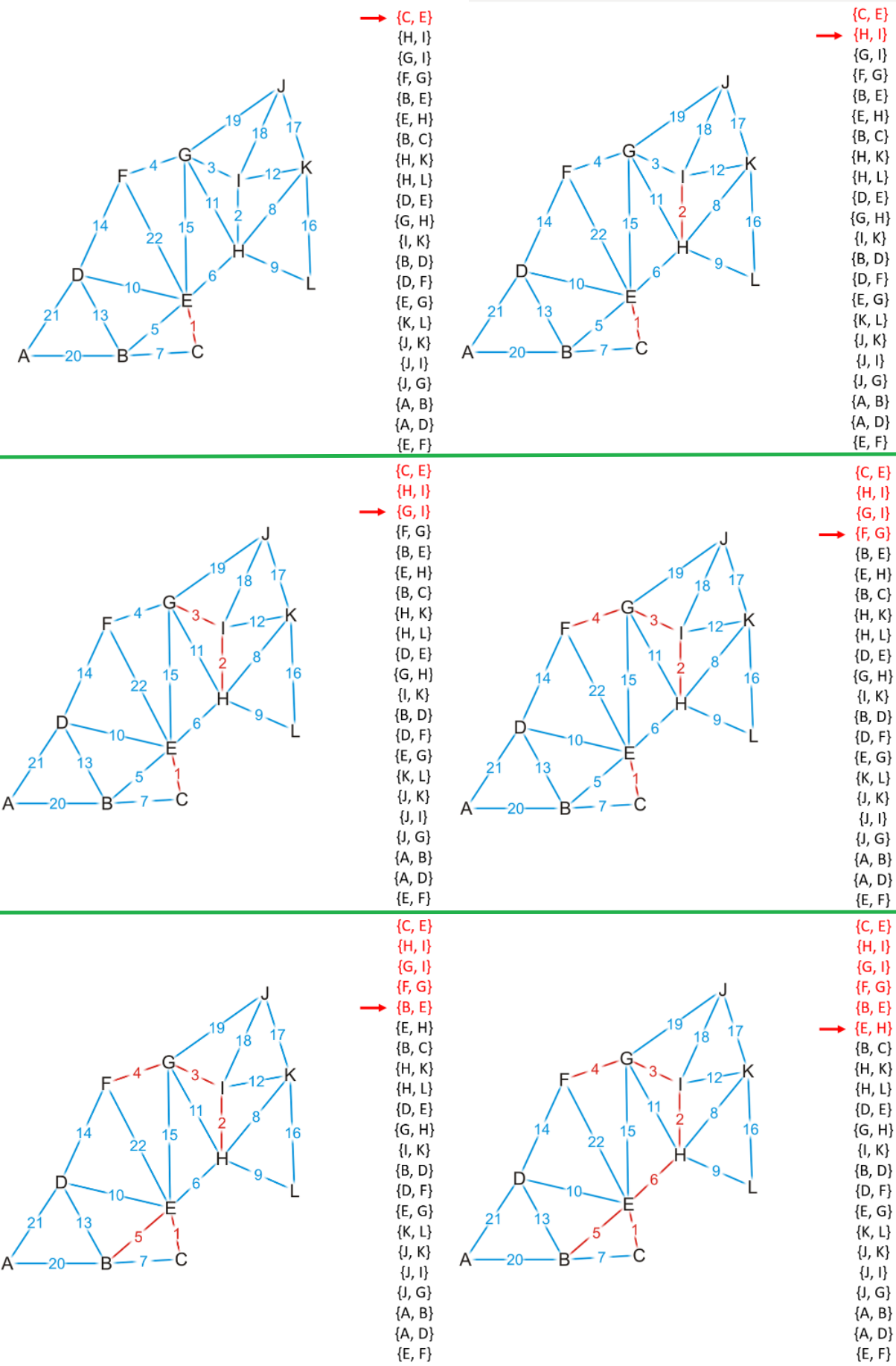
• 然后从最小的边开始将不会导致MST成环的边放入MST中

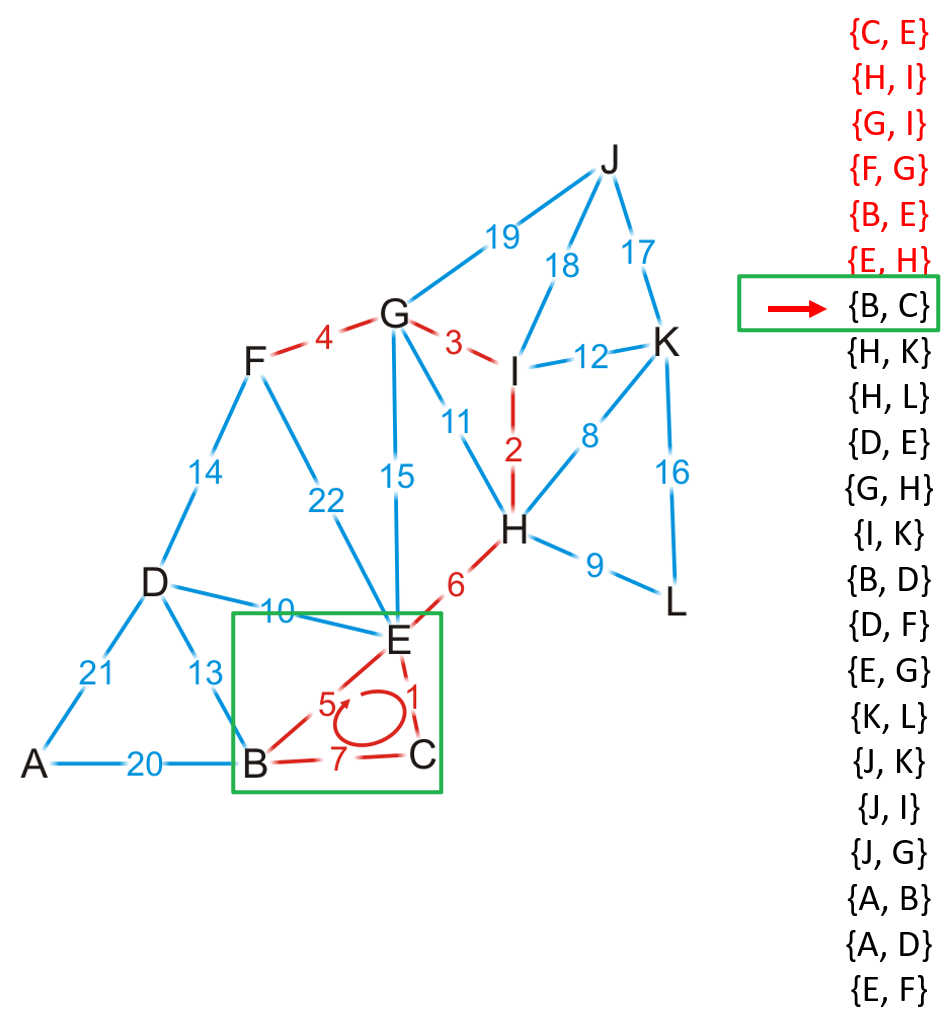
• 如下图的情况中，我们遇到了导致MST成环的边

• 需要跳过这种边，然后继续重复操作

• 注意下面这种大圈也需要能被检测到并跳过

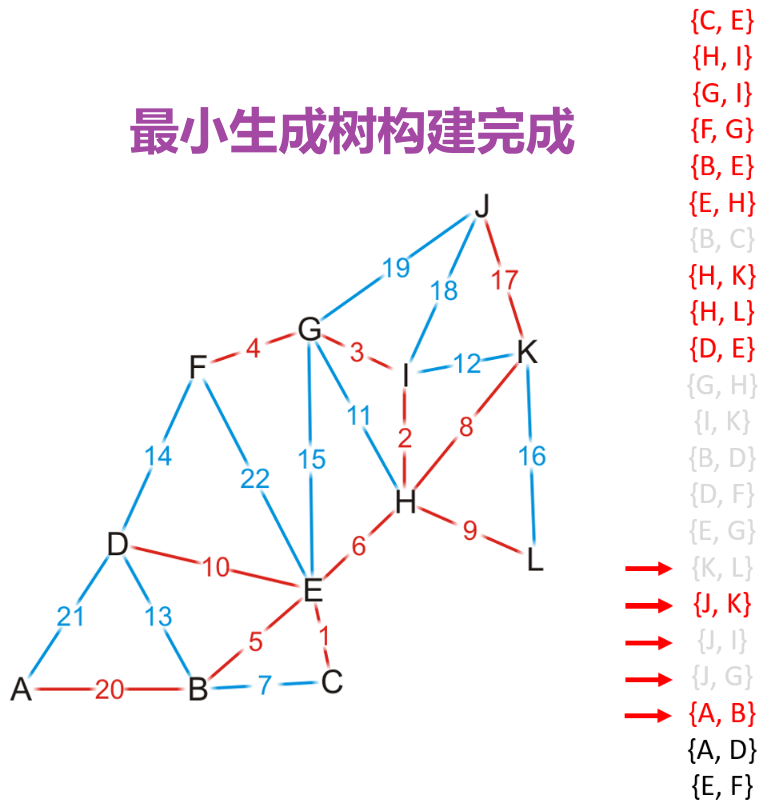
• 重复操作直到MST中有$(|V|-1)$个边时结束，若遍历完了所有边都未能使得MST中有$(|V|-1)$个边，则说明该图是非连通的

3.2 并查集加边

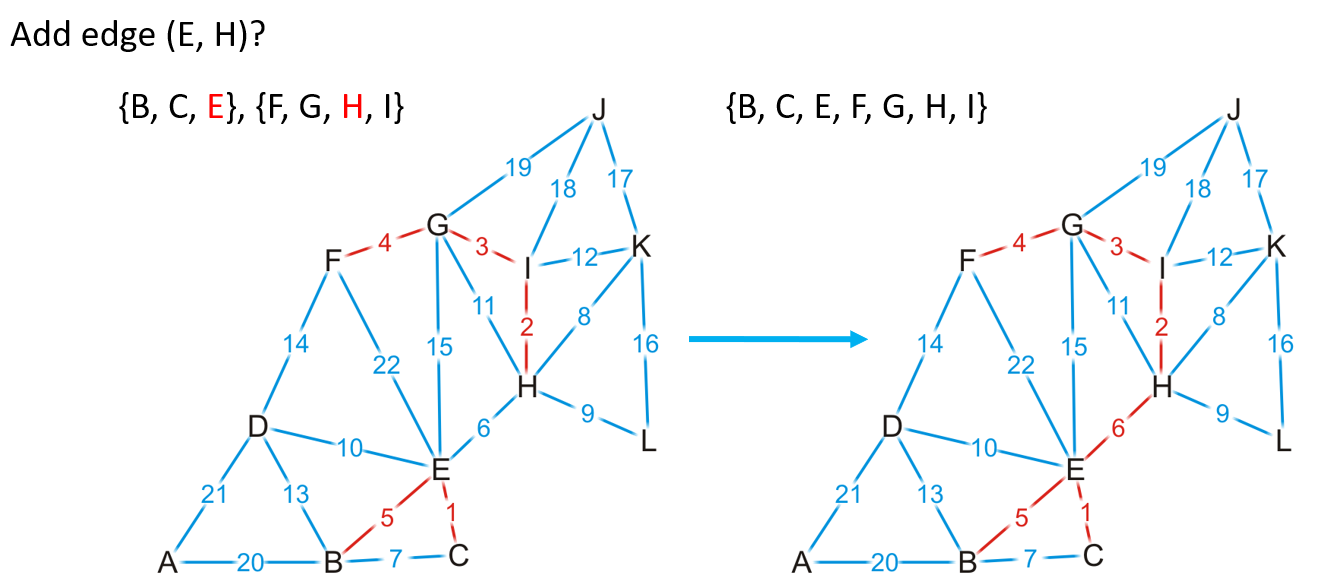
• 在加边过程中，我们将存在于同一个子图中的边所连接的顶点视为一个等价类，整个Kruskal算法过程中使用并查集对MST中的顶点进行存储
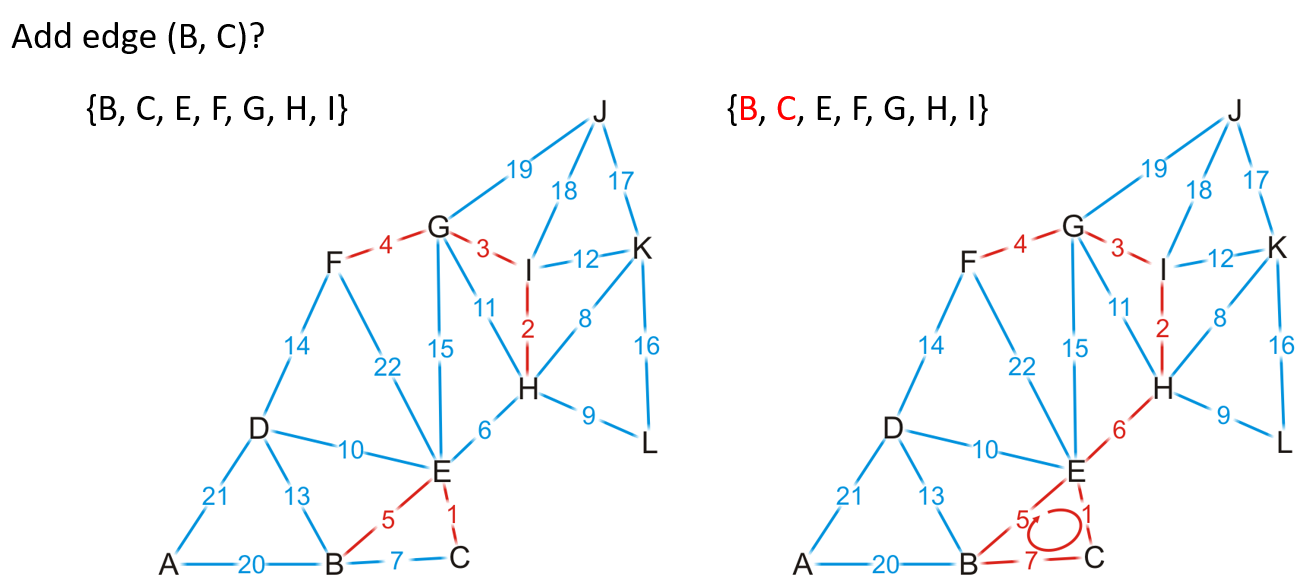
• 如下图所示是加边的过程，如果新增的边连接的两顶点存在于不同的不相交集合中，那么该边的加入就不会导致MST成环

• 如下图中新增的边的两顶点存在于同一个不相交集合中，则会导致成环，需要跳过该边

3.3 算法分析

• 若不使用并查集，而是使用暴力遍历的方式检测成环与否，则此时算法的时间复杂度分析如下
  • 排序：若使用$O(n\ln n)$的排序算法，则对所有边进行排序需时间$O(|E|\cdot\ln|E|)$
  • 加边：每加一条边都需要遍历所有顶点来检测是否成环，时间复杂度为$O(|V|)$，所以检测所有的边需要$O(|E|\cdot|V|)$的复杂度
  • 总共：总的时间复杂度为$O(|E|\cdot\ln|E|+|E|\cdot|V|)$，由于$|E|\leq|V|^2$，所以$\ln|E|\leq2\ln|V|$，故而$O(|E|\cdot\ln|E|)=O(|E|\cdot\ln|V|)$，由于$\ln|V|<|V|$，所以时间复杂度为$O(|E|\cdot|V|)$
• 若使用并查集（并与查操作复杂度均为$O(\alpha(|V|))=O(1)$）来检测已有MST加入新边后是否成环
  • 加边：则每检测一条边，都需要Find该边的两个顶点是否在同一个等价类内，若是则跳过，否则将新建不相交集合或将已有的包含该两个顶点的不相交集合Union，所需时间均为$O(1)$，故而检测所有的$|E|$条边所需的时间复杂度为$O(|E|)$
  • 总共：若存在$O(n)$的排序，则总的时间复杂度就是$O(|E|)$，一般来说还是只能使用$O(n\ln n)$的排序，此时总时间复杂度为$O(|E|\cdot\ln|E|+|E|)=O(|E|\cdot\ln|E|)=O(|E|\cdot\ln|V|)$

3.4 代码实现

• 待补充

四、对比P和K算法

• Prim算法堆优化后的时间复杂度为$O((|V|+|E|)\cdot\ln|V|)$，而Kruskal算法并查集优化后的时间复杂度为$O(|E|\cdot\ln|E|+|E|)$，下面的对比分析引用自OI Wiki
  • Prim的堆优化如果使用二叉堆等不支持$O(1)$复杂度进行堆中顶点边权更新的堆，其复杂度就不优于Kruskal，常数也比Kruskal大
  • 在稠密图中$|E|\approx|V|^2$，尤其是完全图$|E|=|V|^2$的分析中，暴力Prim的复杂度比Kruskal优，但不一定实际跑得更快，所以一般都使用Kruskal算法