最大最小堆与堆排序

从优先队列引入优先级的概念，继而引出最小堆结构，然后顺带介绍堆排序算法

发表于 2024/11/01 更新于 2025/01/06

作者 WhythZ

28 分钟阅读

最大最小堆与堆排序

一、优先队列

1.1 优先级

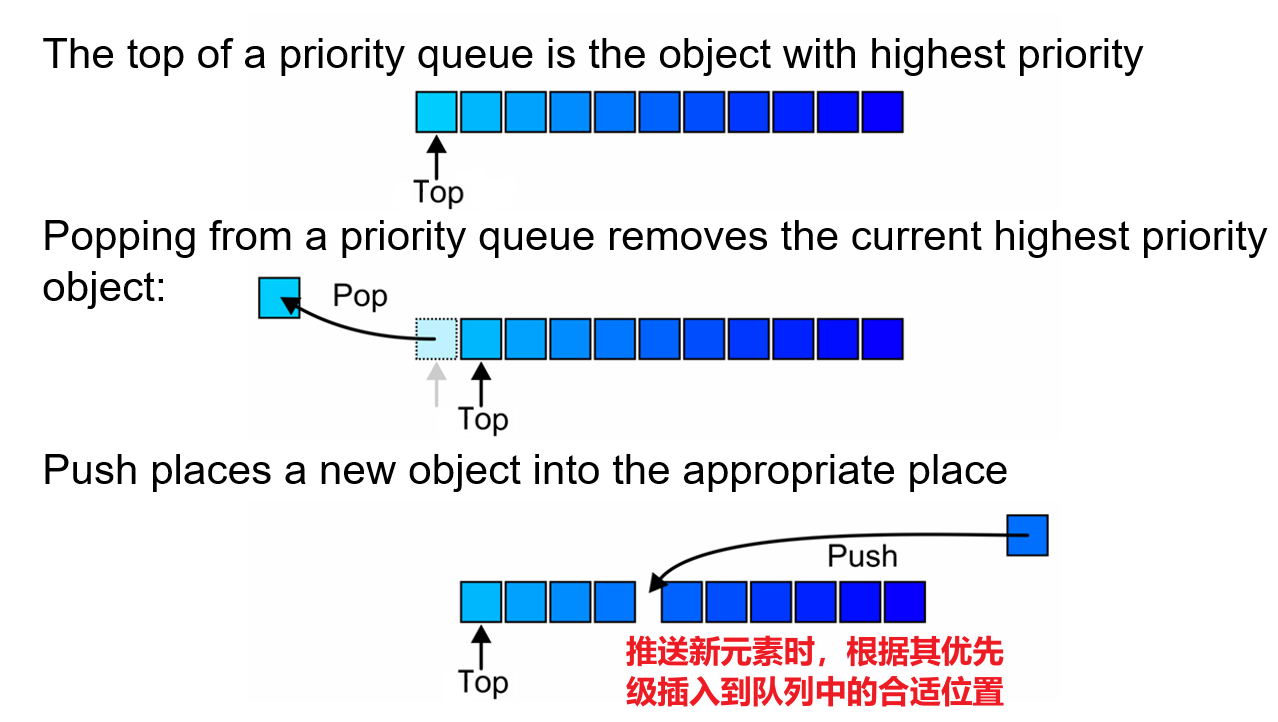
普通的队列是先进先出的，而优先队列（Priority Queue）内的每一个元素均带有优先级属性，优先级高的会被最先取出（队列按优先级排列，最高优先级的在队伍头部）
当我们往队列中添加一个新元素时，会为其附着一个表示优先级的变量，比如一个非负整数，数字越大优先级越低，0是最高优先级，新的元素会按照其优先级被插入到队列中的合适位置

我们也可以通过其他形式表示优先级，比如一个容量为二的元组如下所示

1.2 多队列

如果只采用一个队列，每次插入一个带优先级的新元素的时间复杂度并不是稳定的$O(1)$
假设我们要实现一个优先级总数固定为$M$的优先队列，我们拿$M$个普通队列分别对应各级优先级，将其包装成一个多队列（Multiple Queue）的数据结构
- 每次插入新的元素就依照其优先级将其放入对应的内部队列中，时间复杂度为$O(1)$
- 每次Pop和GetTop的操作复杂度就为$O(M)$
- 缺点就是空间占用更大，且需要限制优先级总数在一个固定的值上

1.3 思考

我们还可以用AVL树来存储一串带有优先级的线性数据，将节点按照优先级进行大小的比较放入树中，但AVL树的各操作（假设我们提供了类似队列的读写方法）的时间复杂度均为$O(\ln(n))$，并且维持树的平衡还会产生额外的开销
有没有一种办法可以让所有的操作的时间复杂度都降为$O(1)$？

二、最小堆

最大堆（Max-Heap）和最小堆只有从上至下的大小排布顺序不同而已，其所有操作和实现及其相关分析均可类比最小堆

2.1 定义与形式

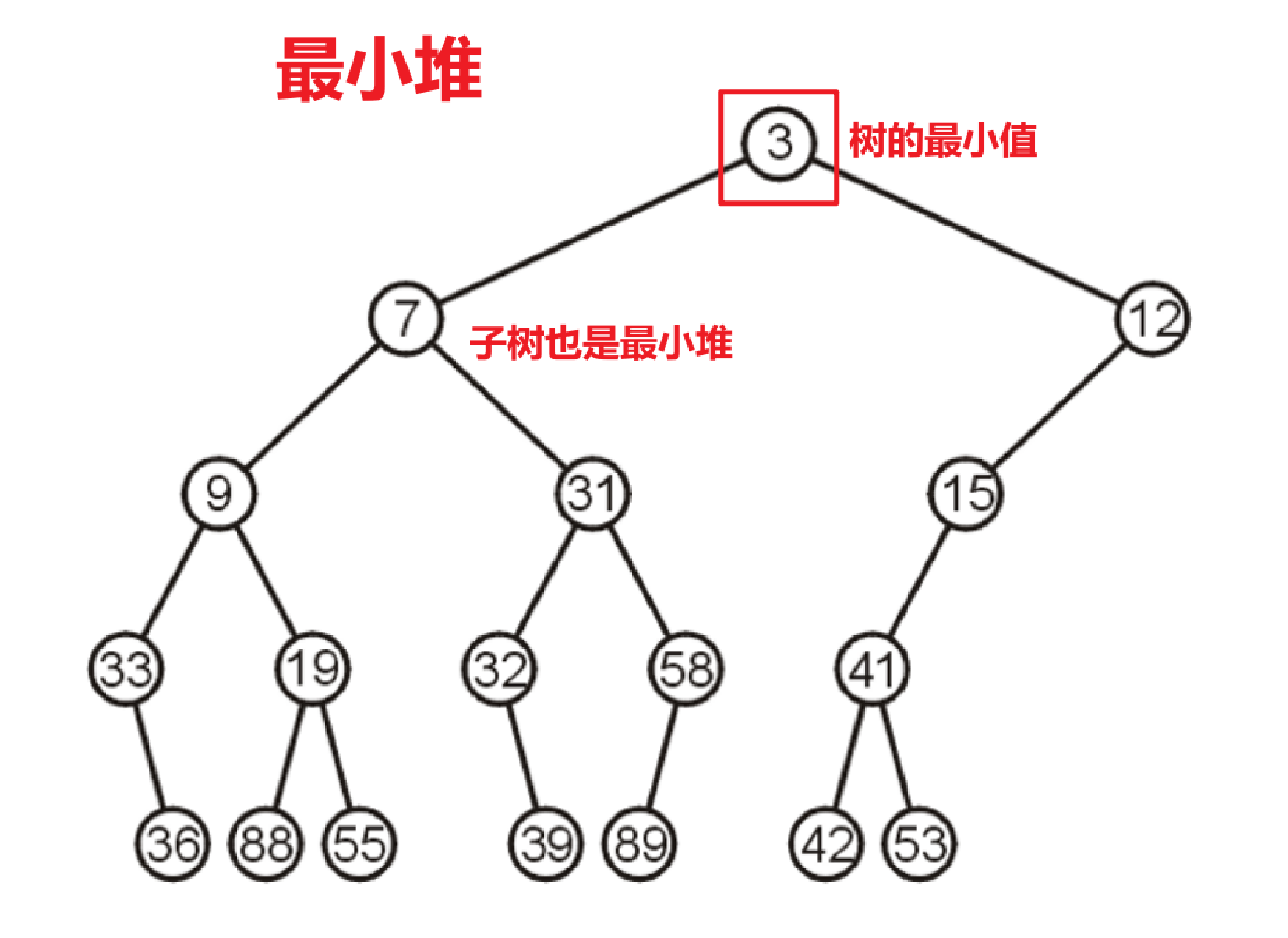
堆（Heap）是一种完全二叉树，在此基础上，最小堆（Min-Heap）满足以下性质
- 根节点的值是整个二叉树中最小的
- 每个节点的两个子树都是最小堆（单个节点也算最小堆）
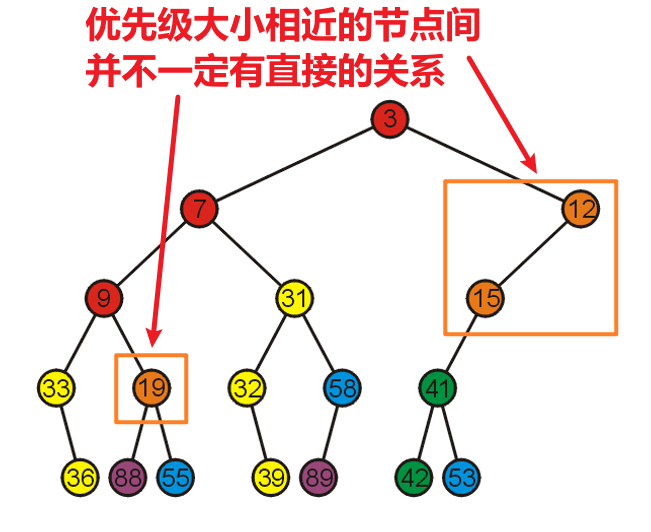
请注意和二叉搜索树不一样，搜索树要求左子树的任意值<根节点值<右子树的任意值；而最小堆要求两个子树的任意值均大于根节点，至于左右子树的值之间的大小关系是无所谓的

2.2 优先级的概念

我们先前讨论了优先队列相关内容，其可以通过多队列或AVL树实现，但操作的时间复杂度均不理想，此处我们将最小堆中的值的大小视为其优先级
我们观察一下在最小堆中优先级从小到大的分布

2.3 增删查操作

2.3.1 `GetTop`操作

最小堆中的GetTop操作（获取最小值）直接获取根节点即可，时间复杂度为$O(1)$

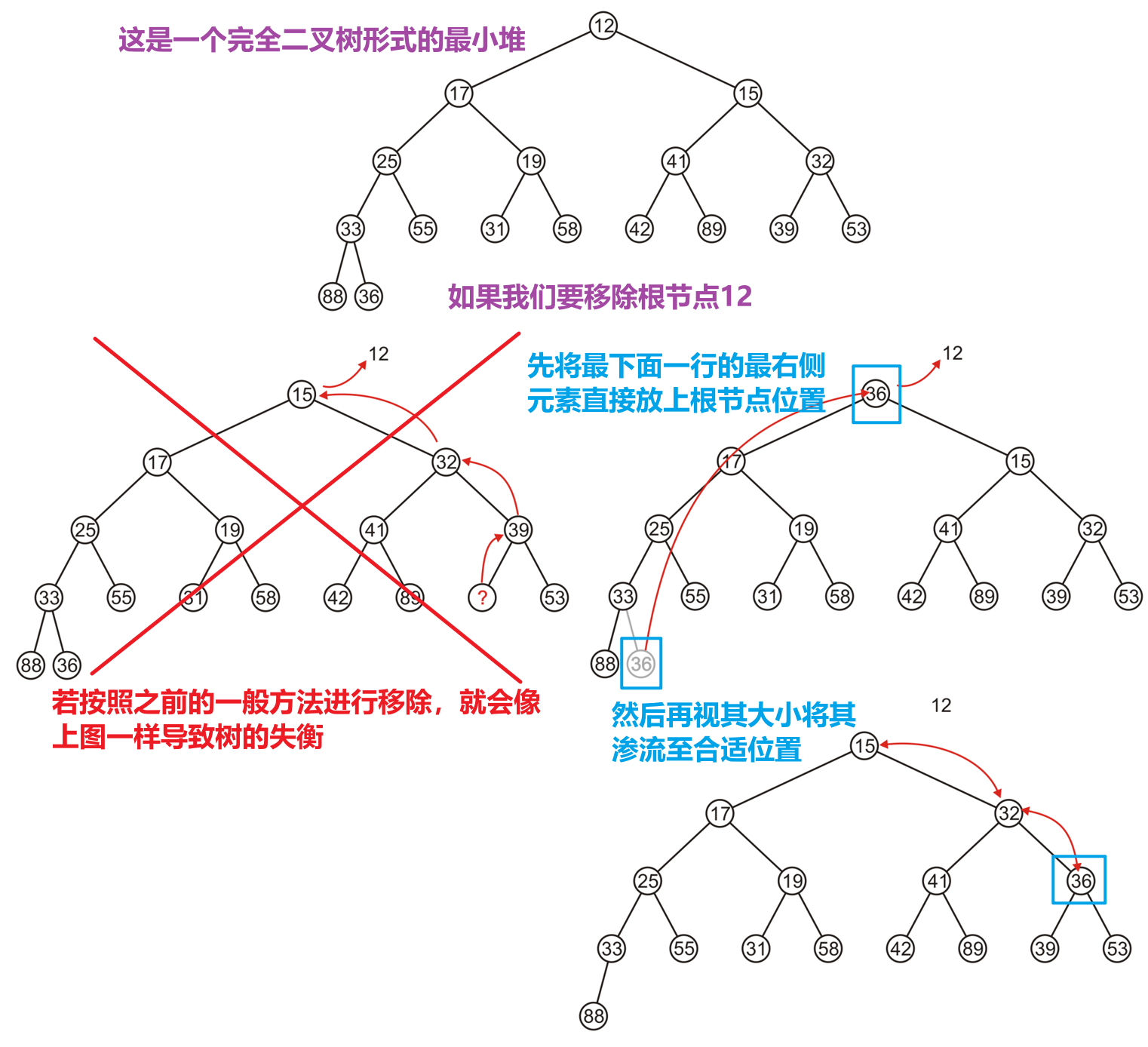
2.3.2 `Pop`操作

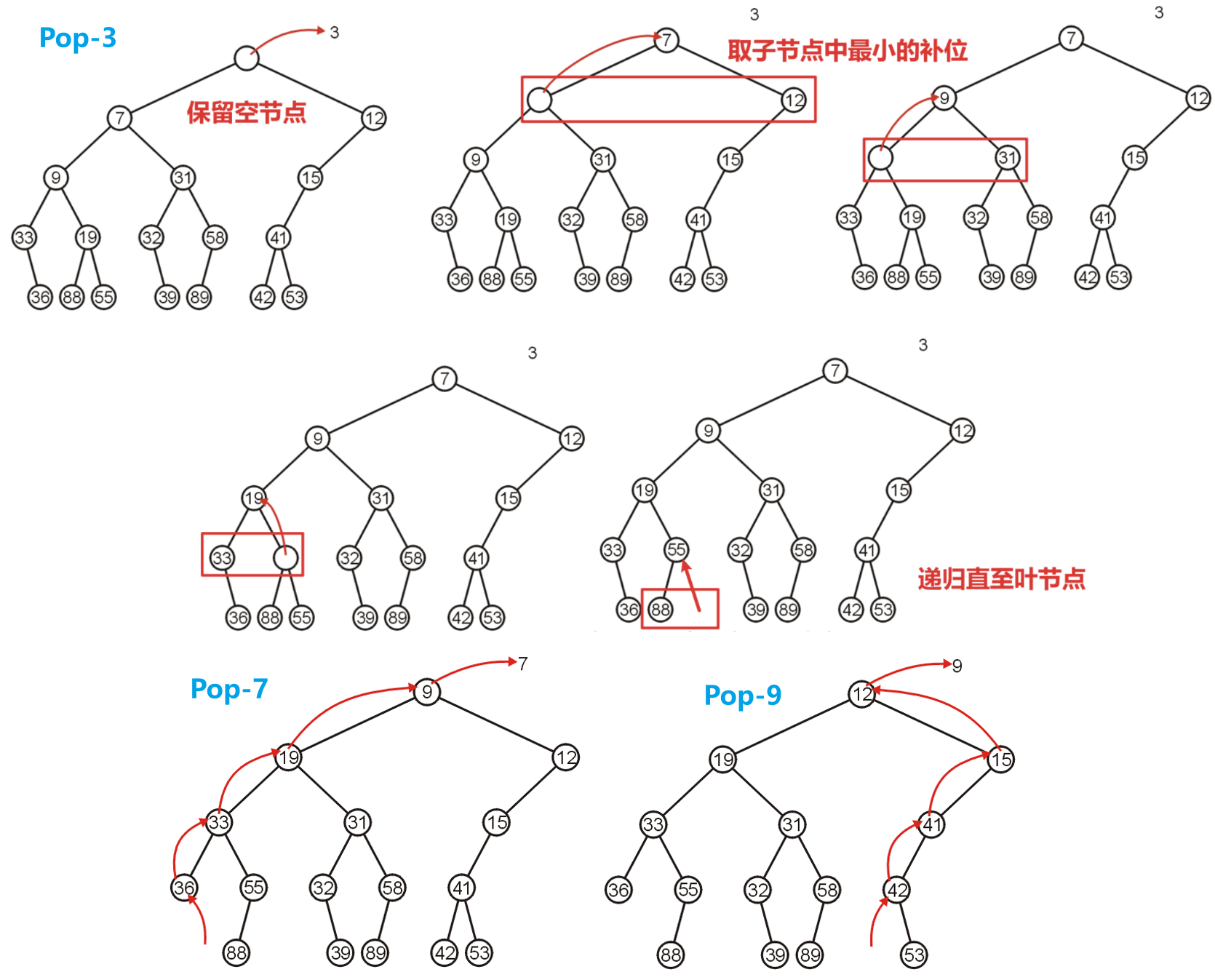
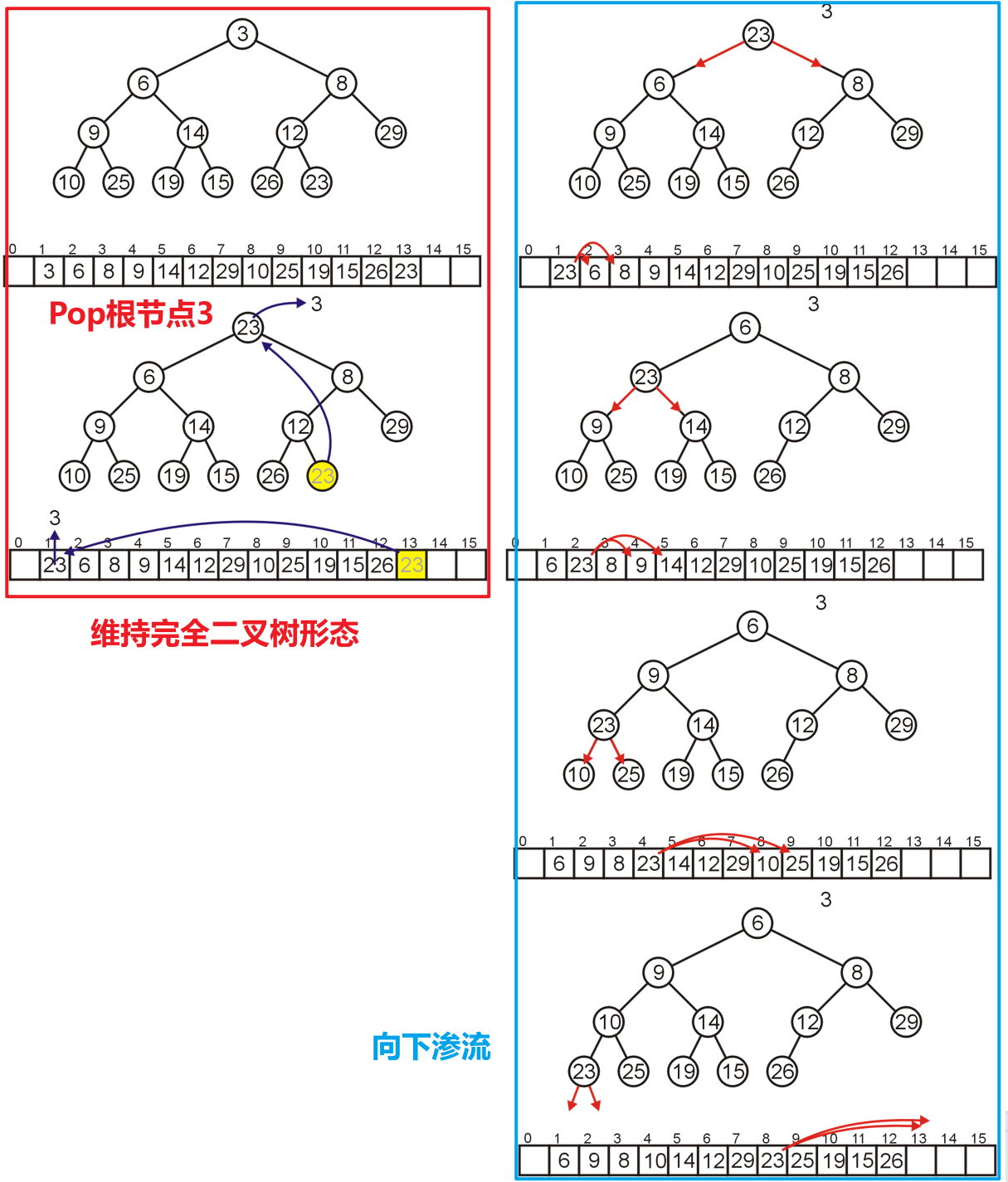
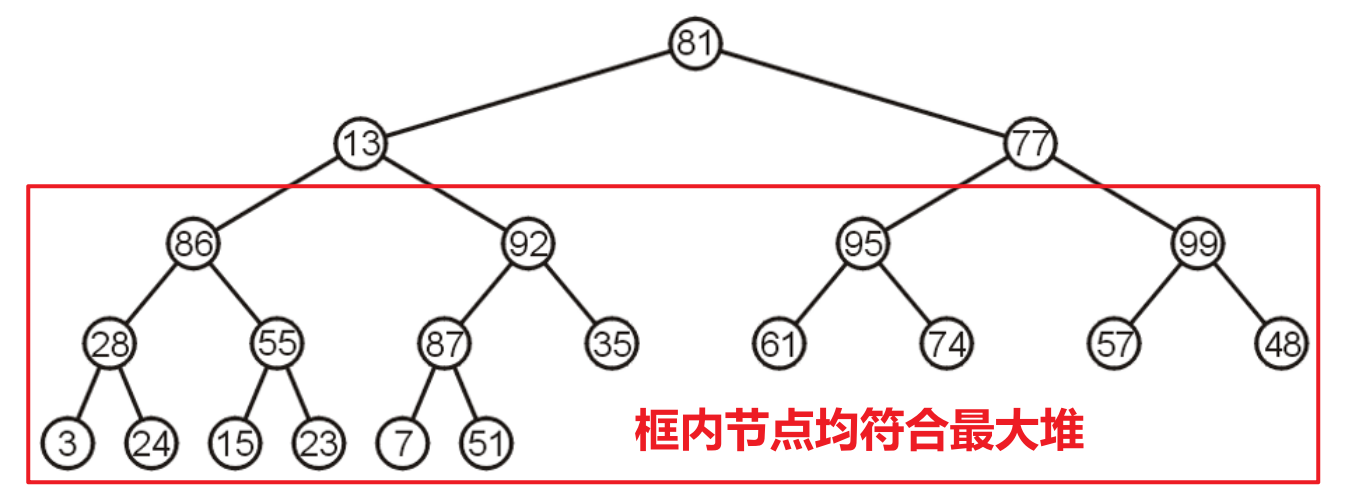
Pop操作就是移除最小值即根节点的值，我们会保留此时的值为空的根节点，从其子结点中选取一个最小的进行补位，然后其原位变空，我们递归进行处理即可，直到抵达某个叶节点
下图对最小堆进行了三次连续的Pop操作演示

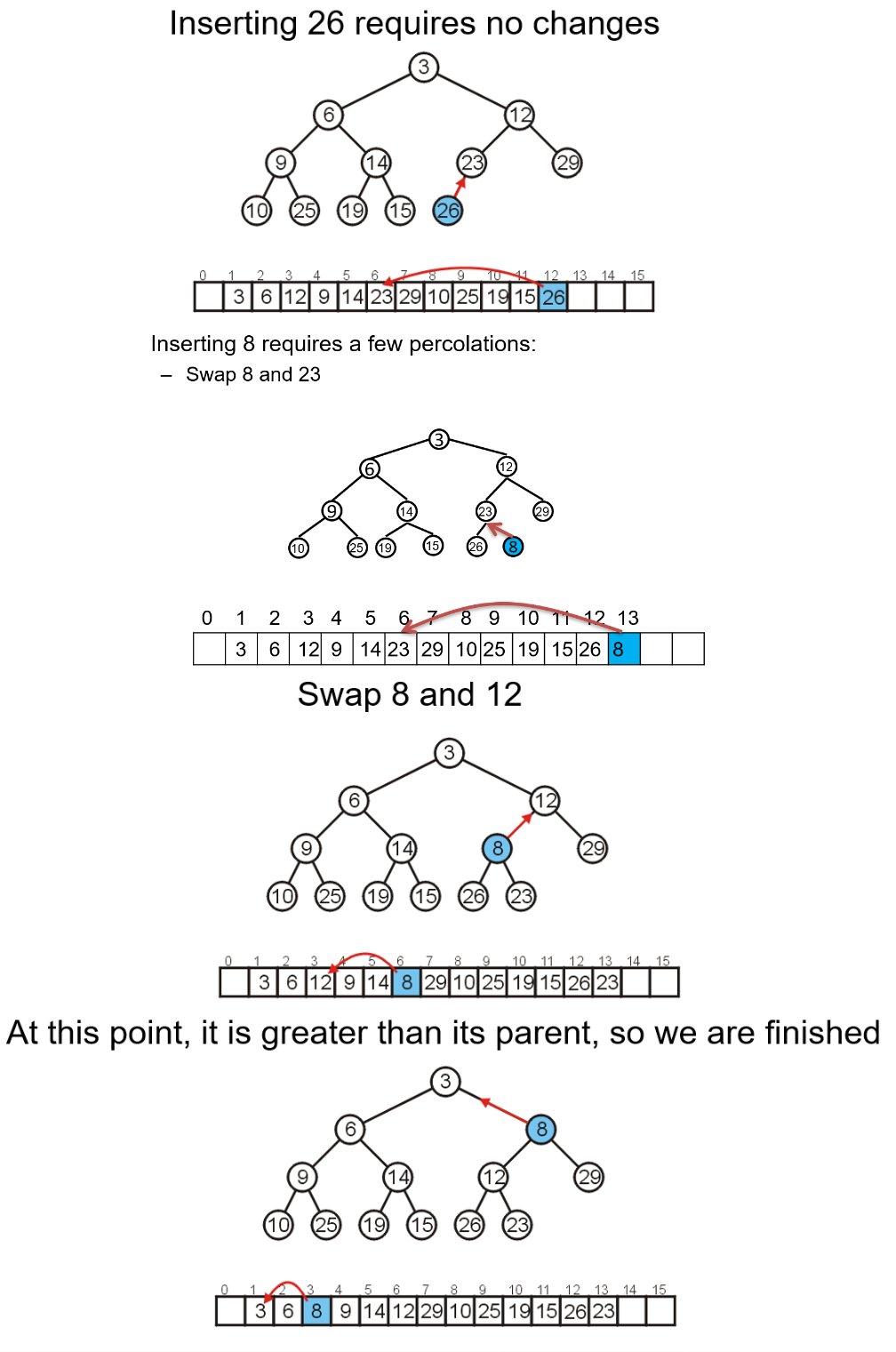
2.3.3 `Push`操作

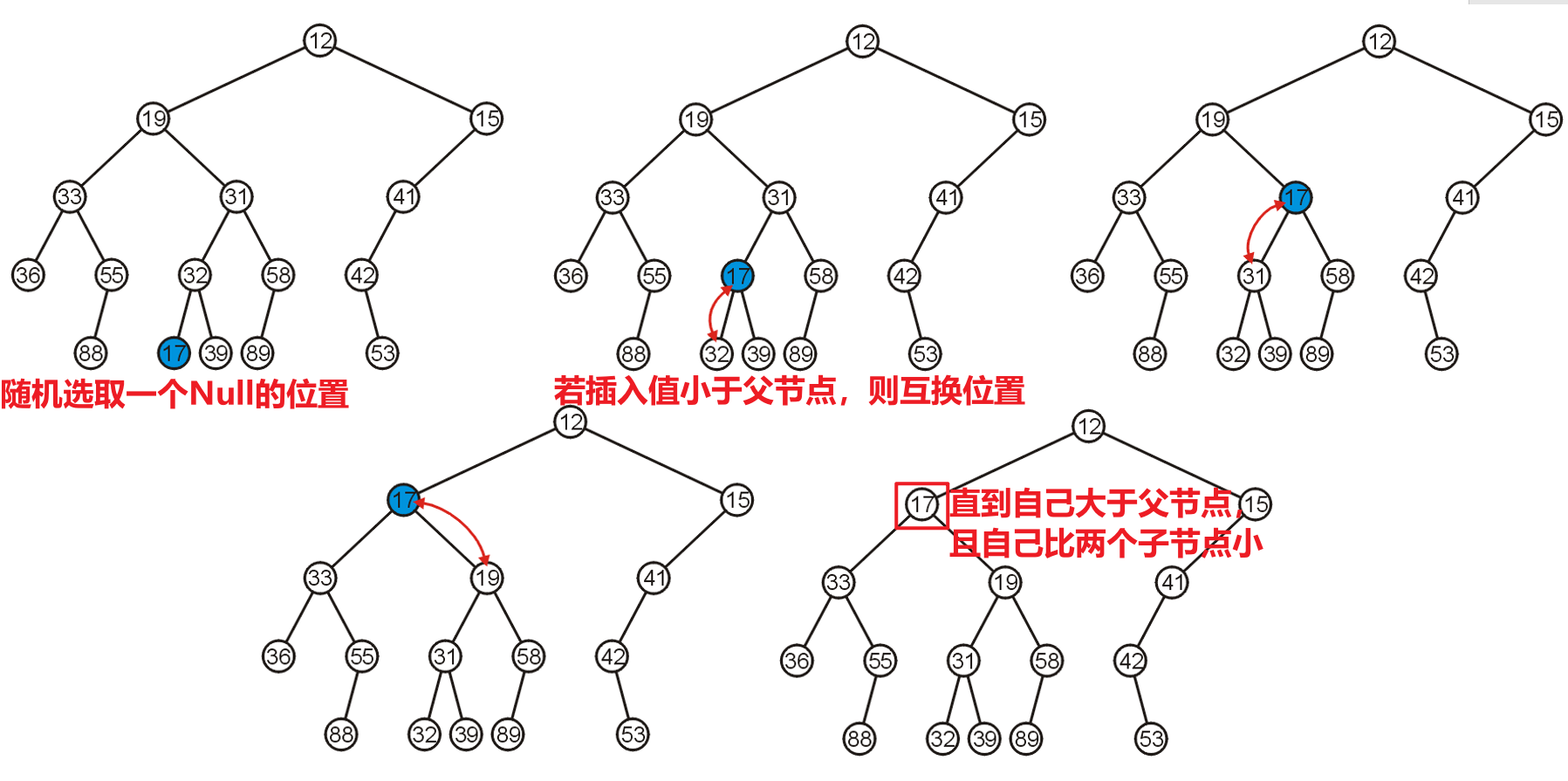
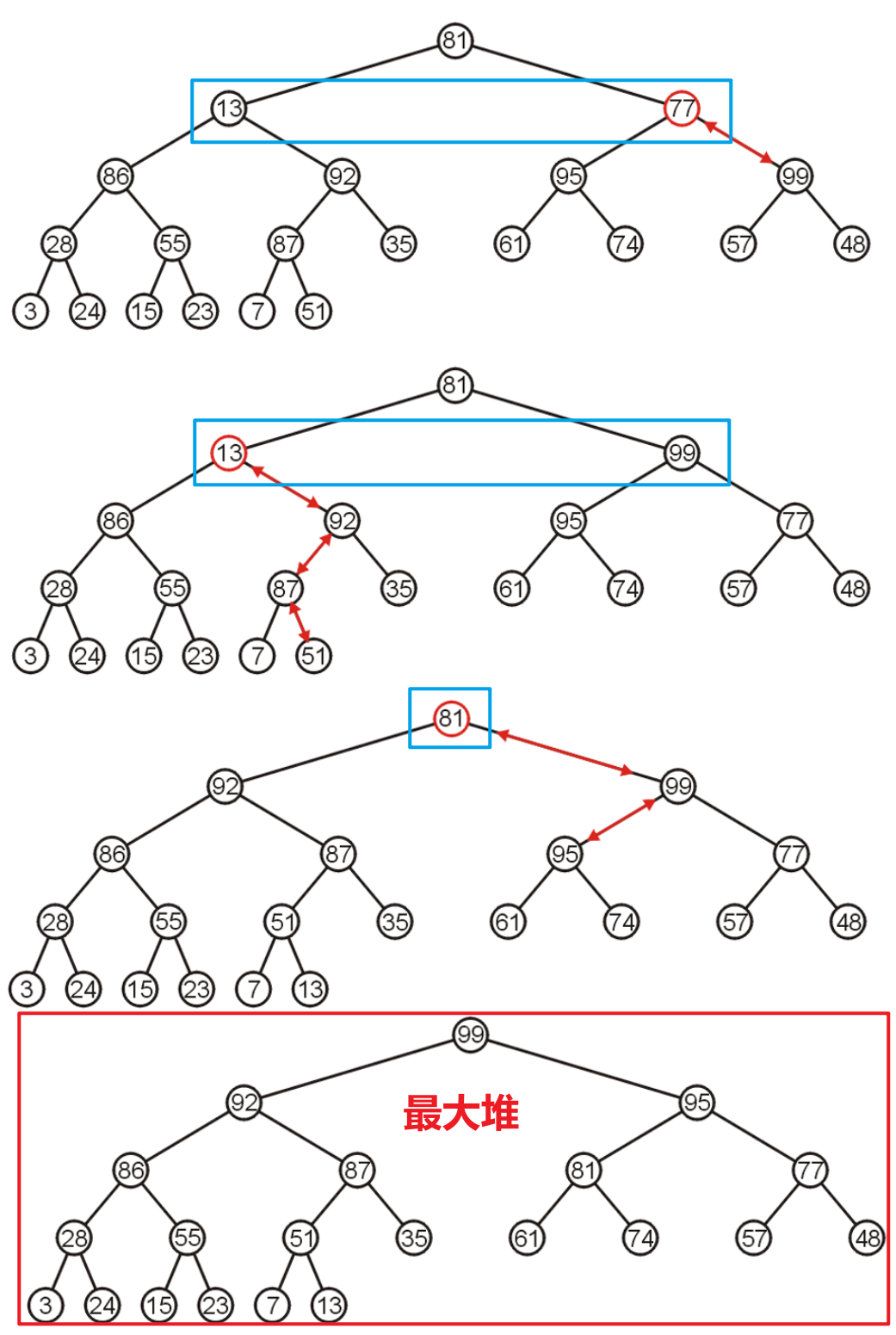
Push操作的其中一种实现方式称是渗流（Percolation），即从任意一个叶节点处插入，然后向上进行交换，直到整个树满足最小堆（即自身比父节点大，且比两个子节点小）
下图是渗流方法的图示，节点$17$一直向上浮动直到自身比父节点大后，检查自己的两个子节点，都比自己大，所以此次Push就完成了（若向上浮动到最后发现自己比某个子节点大，则需要从该分支进行下沉，直到自己比所有子节点小为止）

问题是我们该选取哪个位置进行插入呢？回想最小堆的设计目的就是完成优先队列的类似功能实现，也就是说我们最终是要从最小堆中取出某优先级的节点的，所以我们要保证时间复杂度的最小化，也就是说我们需要让最小堆在Push后保持平衡

2.4 平衡性与数组实现

2.4.1 维持完全二叉树

完全二叉树是平衡的，我们可以将最小堆维持为完全二叉树，以保证搜索效率
为此，我们需要在Push和Pop的时候注意维持树的完全性
- Push在树的末尾叶节点的子节点位置时，只需靠左插入，然后向上渗流（不会导致形变）
- Pop移除根节点时，需要将最右侧的叶节点直接拿来代替根节点，然后向下渗流

2.4.2 数组形式实现

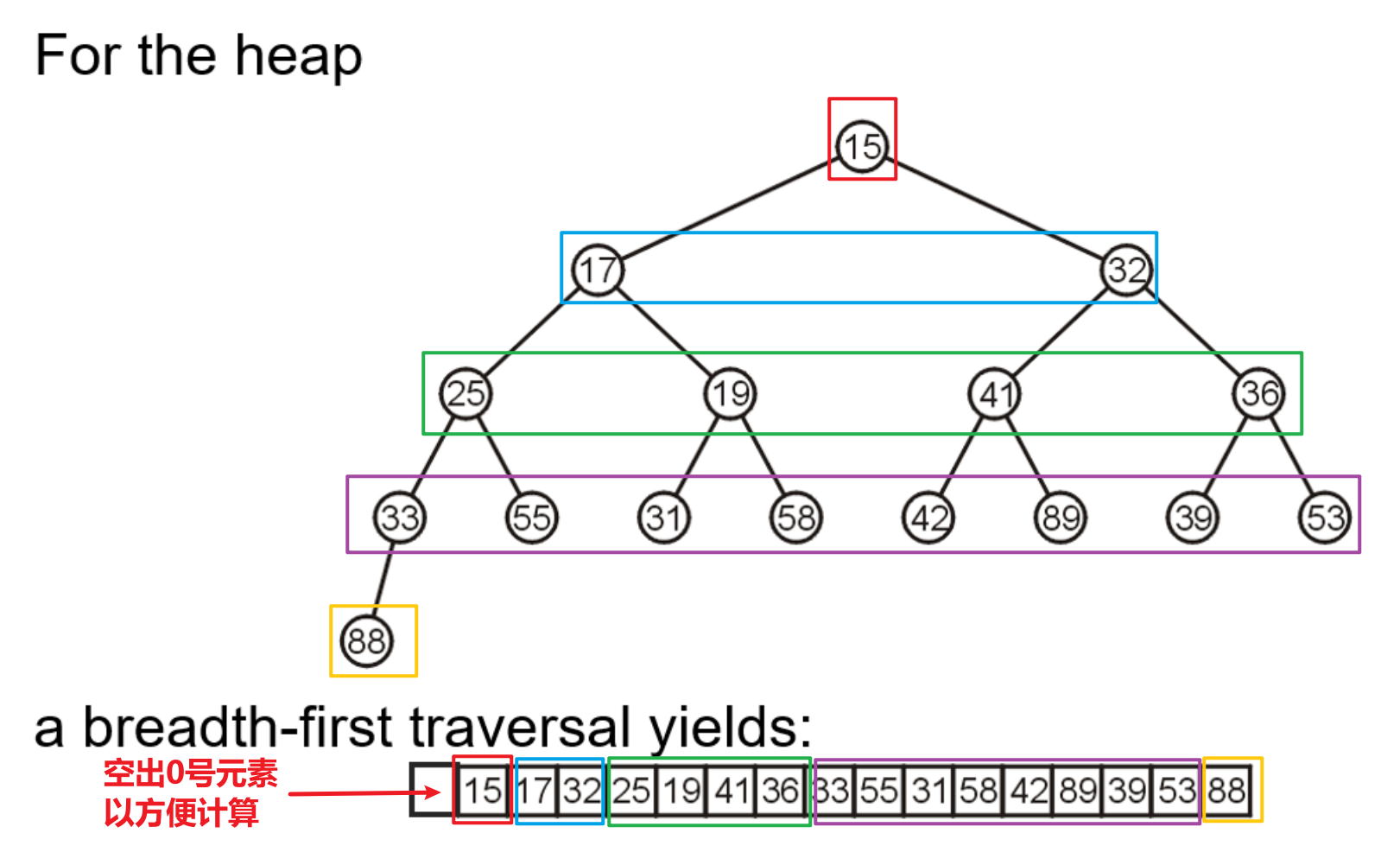
之前的笔记中我们知道完全二叉树可以直接用线性结构进行存储，即通过广度优先遍历整个完全二叉树，将节点值存储在线性表中，比如数组

Push新元素到该最小堆上时，我们将其插入能插入的空节点的最左侧，然后向上渗流

Pop根节点时，我们将最右侧叶节点放到根节点处，然后向下渗流

2.5 时间复杂度分析

最小堆
- GetTop操作：直接获取根节点，$O(1)$
- Push操作：可能需要将新节点向上渗流，复杂度与树高相关，平均$O(\ln(n))$
- Pop操作：剪切到根节点处的叶节点可能需要向下渗流，复杂度与树高相关，平均$O(\ln(n))$
斐波那契堆（本文未介绍，仅作对比）
- 插入节点：$O(1)$
- 移动节点（更新节点值并更新位置）：$O(1)$
- 删除节点（并将其余节点复位）：$O(\ln{n})$

2.6 代码实现

最小堆我们已经很清楚了，以下给出了一个最大堆的实现（详细实现参考我的代码仓库），该实现的内核数组并未空出0索引处的位置，没别的原因，我就是不想空出

  
//最大堆的数组形式实现
template <typename T>
class MaxHeap
{
private:
    std::vector<T> array;           //以数组形式存储完全二叉树形状的堆
    size_t height = 0;              //维护一个表示二叉树高度的值

public:
    void PrintTree() const;         //以最大堆的形式可视化打印该数组
    T GetTop() const;               //获取堆顶元素的值

    void Push(T);                   //将新元素推送到堆中并维持平衡
    void Pop();                     //弹出堆顶元素并维持平衡
    
private:
    void PrintLayer(size_t) const;  //打印对应深度的二叉树层

    //获取迭代器对应元素的索引值
    size_t GetIdxFromItr(typename std::vector<T>::iterator);
    //以迭代器获取其指代元素的父节点、左右子节点的迭代器
    typename std::vector<T>::iterator GetParentItr(typename std::vector<T>::iterator);
    typename std::vector<T>::iterator GetLChildItr(typename std::vector<T>::iterator);
    typename std::vector<T>::iterator GetRChildItr(typename std::vector<T>::iterator);
    
    //以迭代器锁定堆中元素，对其进行向上或向下的渗流操作
    void PercolateUp(typename std::vector<T>::iterator);
    void PercolateDown(typename std::vector<T>::iterator);
};

三、堆排序

3.1 原理解析

3.1.1 算法原型及其时间复杂度

我们可以将整个乱序列表放入一个最小或最大堆中，然后进行$n$次的根节点Pop即可得到从小到大或从大到小排列的元素（思考：为什么不用二叉搜索树？因为仅仅排个序，只用最大堆就能完成的任务没必要用搜索树，其为了在Push和Pop后维持其平衡会浪费很多性能）
我们在堆的相关章节笔记中已知，最小和最大堆的Pop与Push操作的复杂度都平均为$O(\ln{n})$，所以长度为$n$的列表的堆排序平均耗费的渐进时间复杂度为

\[O(\Sigma_{k=1}^{n}{\ln{k}})=O(\ln{n!})=O(n\ln{n})\]

3.1.2 设法降低空间复杂度

如果只是简单地构建一个额外的堆，将被排序的列表元素逐一Push进去并按序取出的话，这会耗费$n\cdot sizeof(T)$的内存空间，这并是不我们想要的In-Place（空间复杂度为$O(1)$）的算法
我们可以将乱序列表本身理解为完全（Complete）二叉树形式
- 因为最大最小堆是完全二叉树，而完全二叉树是可以用数组形式存储的（一般来说该实现会空出索引0的位置，而反过来将数组理解为完全二叉树的话就并无此空，这会导致父子节点的关联计算公式有所不同）
- 此时以$O(1)$空间复杂度将乱序列表代表的完全二叉树变形为堆（In-place Heapification）后就可以通过将其变形为最大堆然后通过Pop根节点完成排序

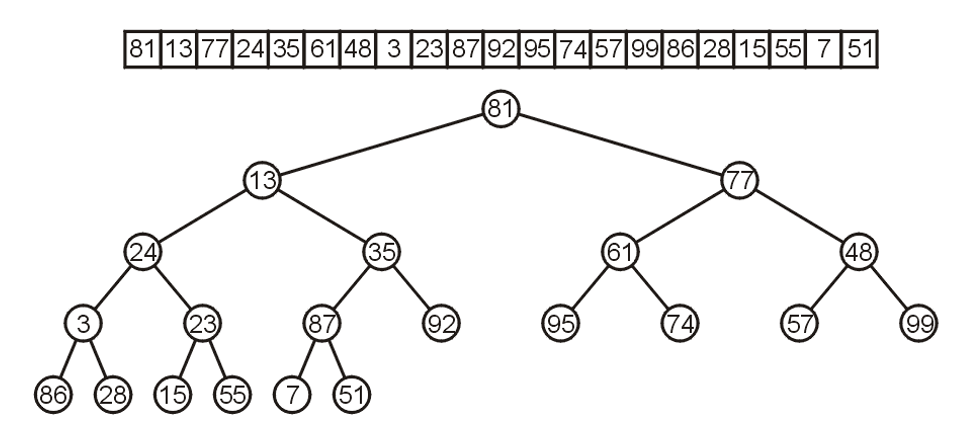
3.1.3 将乱序列表化为最大堆

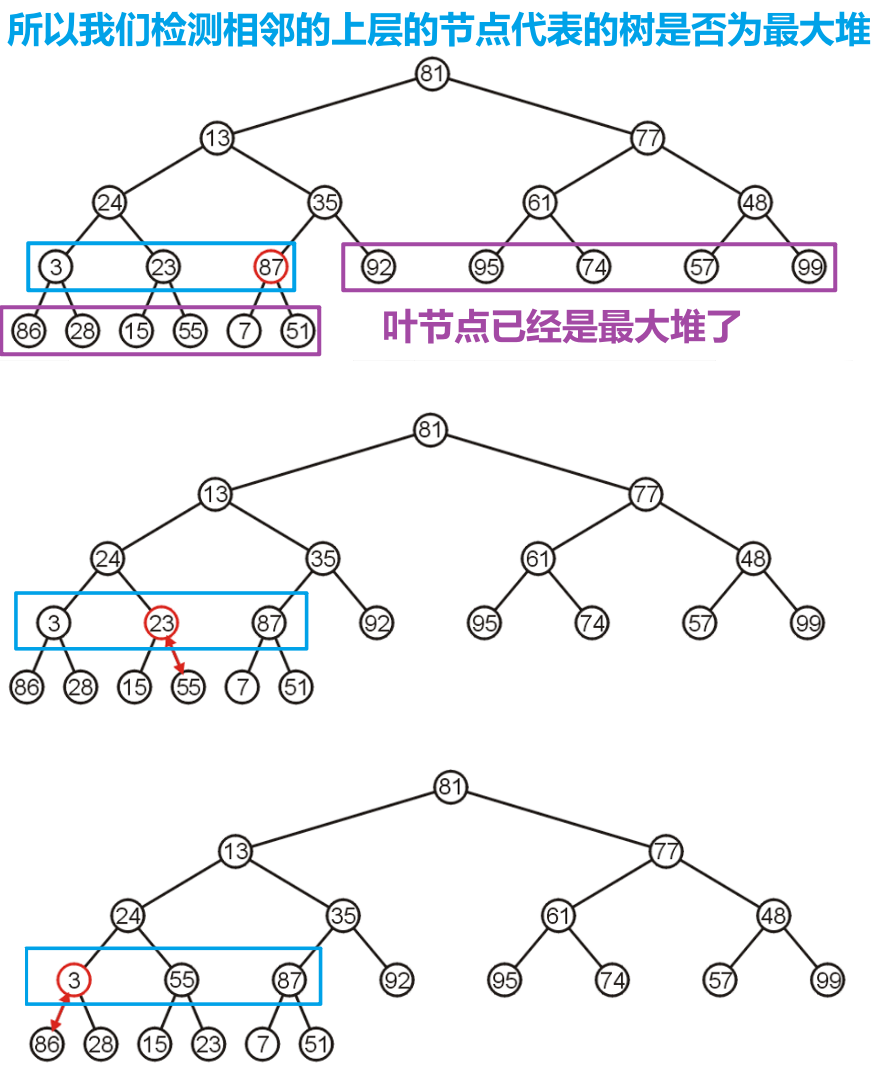
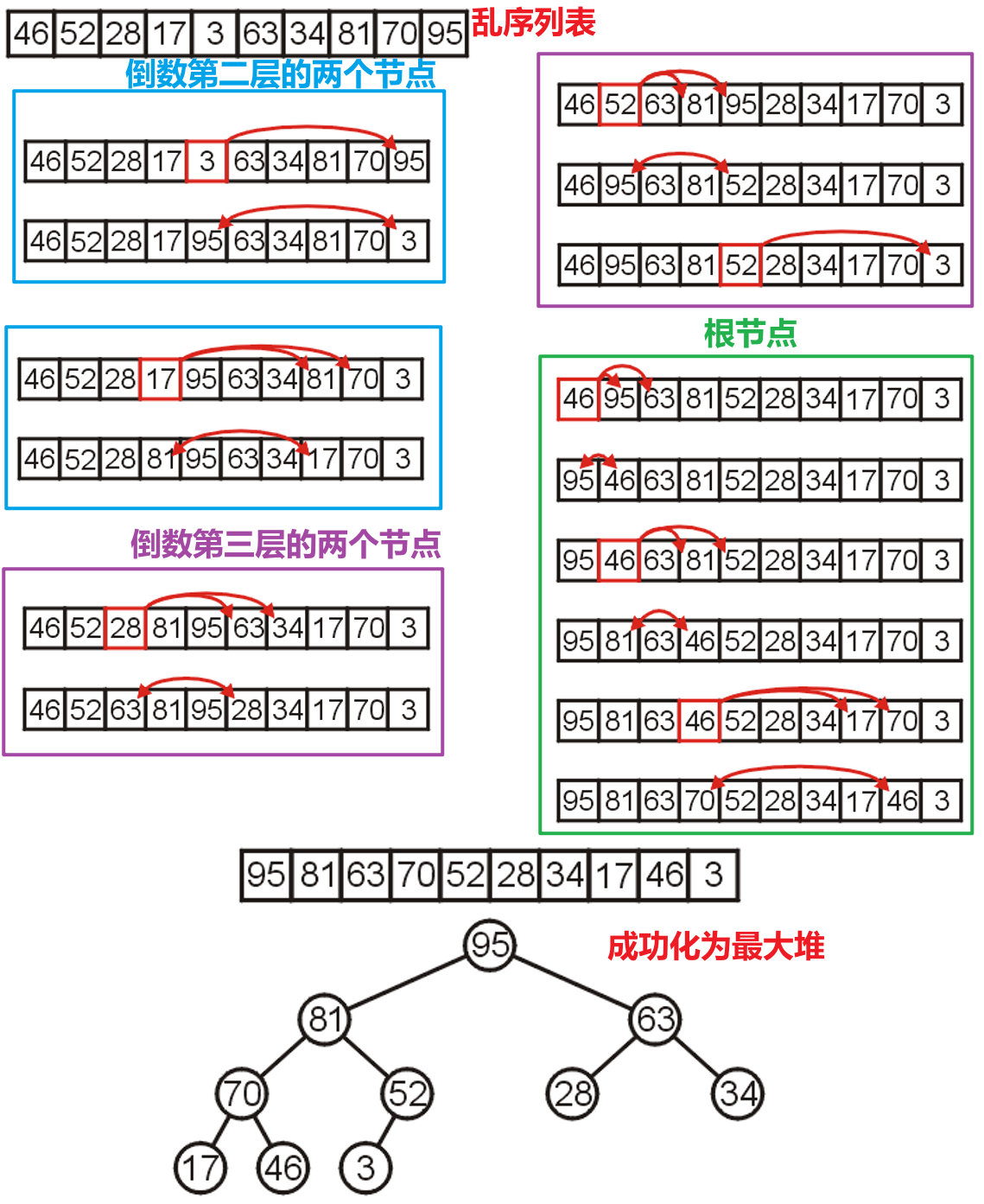
我们对乱序列表代表的完全二叉树自下而上逐层检测是否符合最大堆的定义，若不符合则采取向下或向上渗流的方式使其符合，这样从树的底层遍历到顶层后，该树便成为了最大堆
由于底层的叶节点本身就是一个最大堆，所以直接检测倒数第二层的节点，对于每个节点，需要与两个子节点进行比较，确保三者中最大的处于父节点位置

然后检测到数第三层的节点

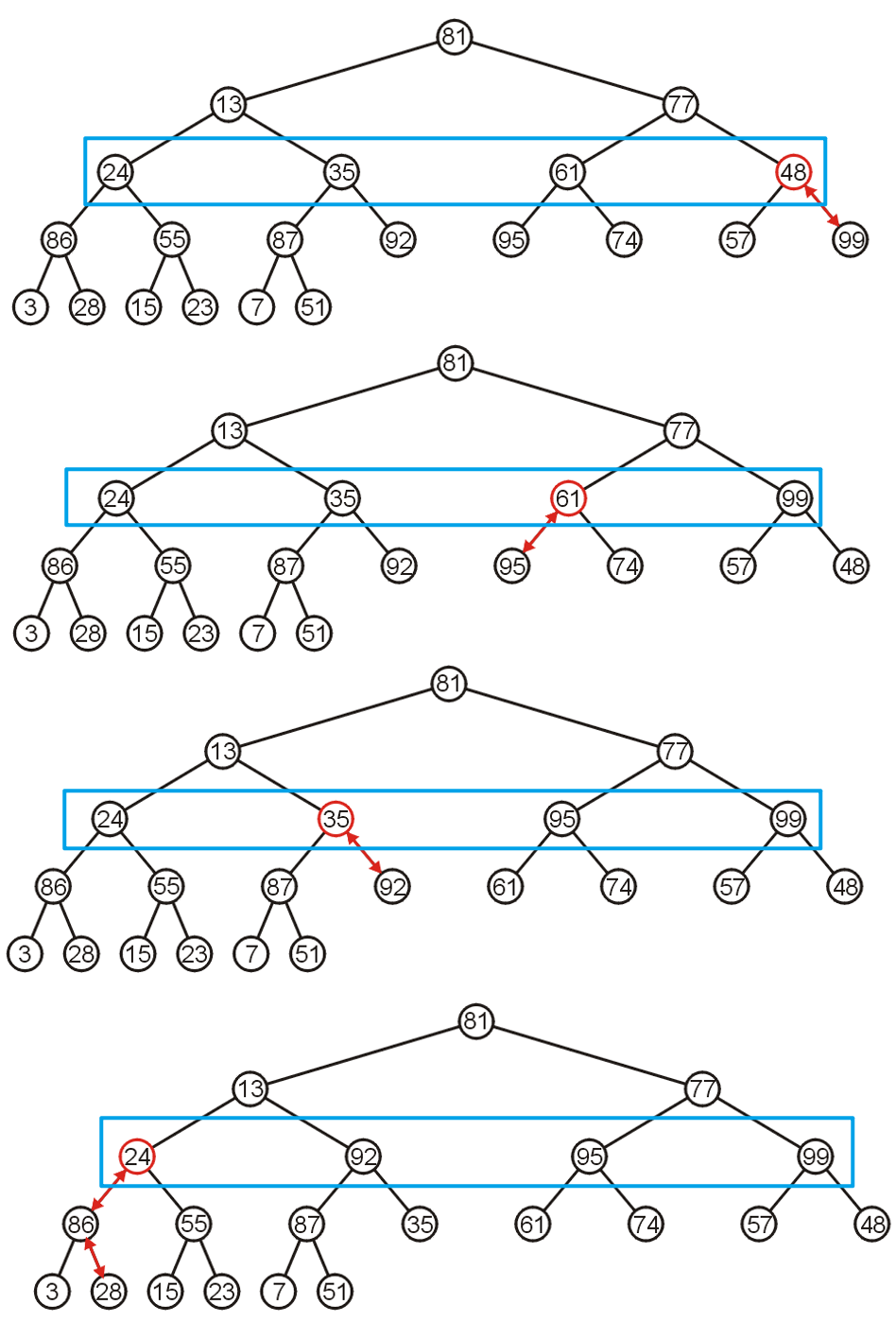
此时我们可以注意到，我们经过上述步骤检测过的三层，节点均符合最大堆的要求

然后我们检测剩下的最上层的两层，即可将整体变为最大堆

上述过程均可以在数组中进行（掌握父子节点的索引大小映射关系即可），下面是另一个例子

3.2 复杂度分析

3.2.1 空间复杂度

空间复杂度我们通过上面的分析已经降为了常数级的$O(1)$

3.2.2 从列表化为最大堆的时间复杂度

时间复杂度则与渗流过程中发生的std::swap操作次数相关，对于检测的每一层的每个节点，其最坏情况（需要最多的std::swap操作）需要渗流到最底层

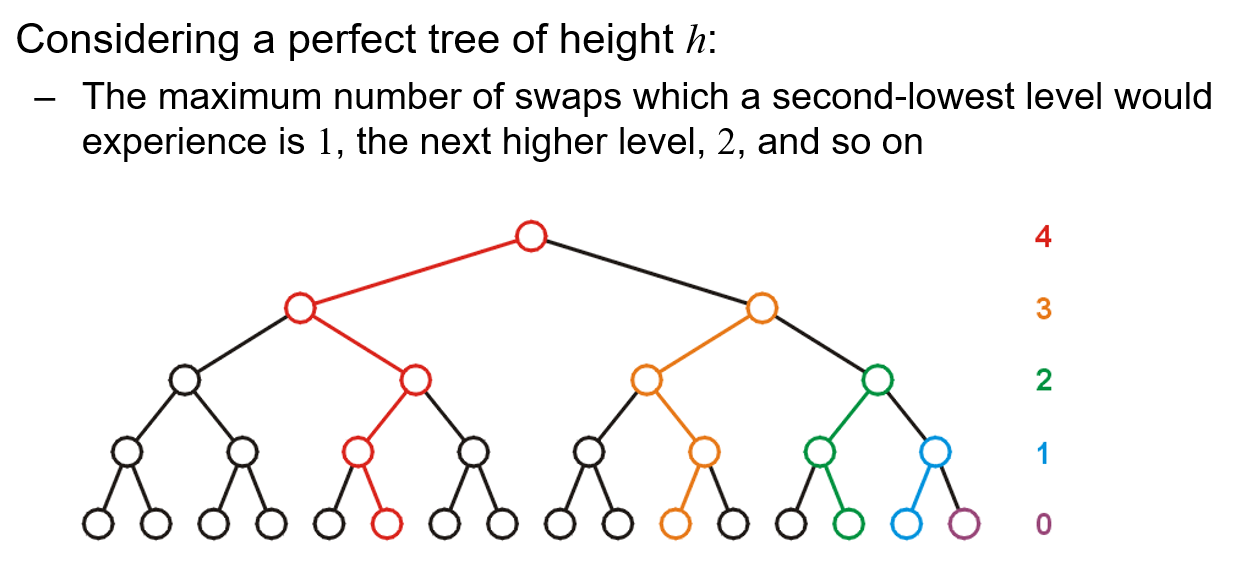
对于高度为$h$的二叉树，其深度为$k$的层共有$2^k$个节点，最坏需要向下渗流$(h-k)$层，即发生$(h-k)$次std::swap，结合完美二叉树的总节点数$n=2^{h+1}-1$，我们就可以得出最坏需要进行的交换次数为

\[\begin{aligned} \Sigma_{k=0}^{h}{2^k(h-k)}&=2^{h+1}-h-2 \\ &=n-\log_2(n+1) \end{aligned}\]

因为每次std::swap需要进行两次比较操作（因为不是二叉搜索树，堆中的两子节点间的相对大小是不确定的，所以需与两个子节点分别进行比较后确定谁是最大的），所以可得堆排序中的比较操作最坏的时间复杂度为

\[O(2(n-\log_2(n+1)))=O(n)\]

3.2.3 从最大堆化为有序列表的时间复杂度

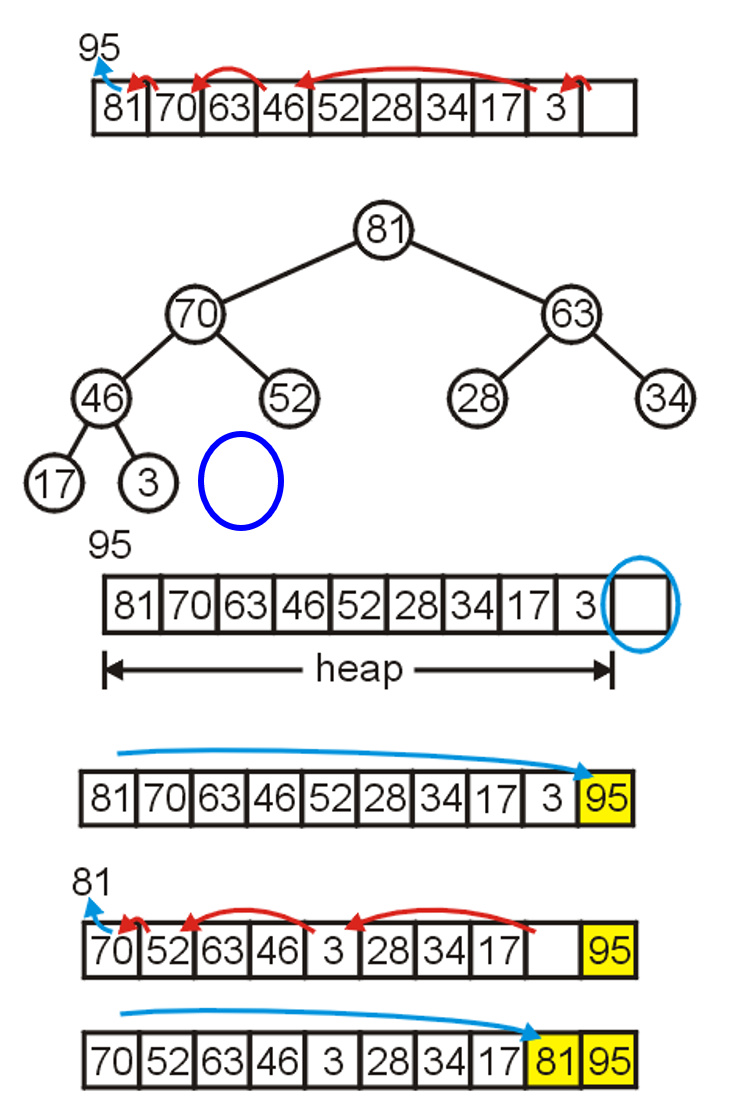
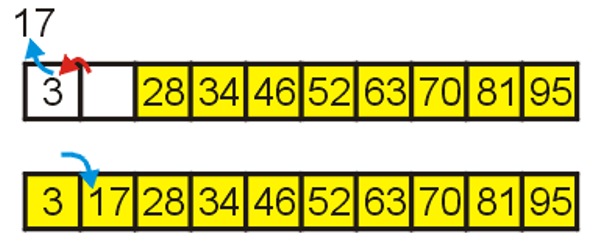
我们从最大堆中将根节点，即列表的最大值Pop出来，该操作的具体流程参考我关于堆的相关笔记，此时会发现列表末端空了出来，正好用于存放刚Pop出的最大值

进行$(n-1)$次该操作后，列表即变为有序

由相关笔记已知，每次Pop操作耗费的时间复杂度与树的高度相关，平均为$O(\ln{n})$，所以进行$(n-1)$次Pop后的时间复杂度为$O(n\ln{n})$

3.2.4 综合分析时间复杂度

结合前两个部分的分析，堆排序的总时间复杂度平均为为

\[O(n)+O(n\ln{n}) = O(n\ln{n})\]

堆排序没有最坏的情况，最优的情况即大部分元素都相等时，复杂度为$O(n)$

3.3 代码实现

  
//向下渗流，传入一个尺寸而不是直接使用_list.size()的原因是我们在最后将最大堆变为有序列表的过程中，需要利用到列表末尾的空位来存放每轮Pop出来的堆顶值x
//在Pop之后我们会将列表末尾的y放到堆顶让其向下渗流，此时我们若不手动限制_size的话，刚刚被我们Pop出来放到列表尾部的值x又会被渗流下来的y所取代
template <typename T>
void PercolateDown(std::vector<T>& _list, size_t _size, typename std::vector<T>::iterator& _itr)
{
    //用于存储指向_itr的两个子节点的迭代器
    typename std::vector<T>::iterator _l, _r;

    //获取_itr在列表中的索引
    size_t _idxItr = std::distance(_list.begin(), _itr);
    //获取左右子节点的索引值，若超出范围则说明没有，直接置空
    size_t _idxR = 2 * _idxItr + 2;
    _r = (_idxR >= _size) ? _list.end() : _list.begin() + _idxR;
    size_t _idxL = 2 * _idxItr + 1;
    _l = (_idxL >= _size) ? _list.end() : _list.begin() + _idxL;

    //若到达叶节点，则直接返回（此处_list.end()是作为类似nullptr的存在）
    if (_l == _list.end() && _r == _list.end())
        return;

    //获取左右子节点中值最大的那个
    typename std::vector<T>::iterator _maxChild = (*_l > *_r) ? _l : _r;
    if (*_itr < *_maxChild)
    {
        //交换二者位置确保大的在上面（std::iter_swap并未交换两个迭代器指向的位置，交换的是两个位置上的值）
        std::iter_swap(_itr, _maxChild);
        //递归调用向下渗流
        PercolateDown(_list, _size, _maxChild);
    }
}

//堆排序：
template <typename T>
void HeapSort(std::vector<T>& _list)
{
    //传入列表的底层开始，向上逐层遍历，让每个节点向下渗流，经历此循环n次后列表便变形为了最大堆
    for (typename std::vector<T>::iterator _itr = _list.end() - 1; _itr >= _list.begin(); _itr--)
    {
        PercolateDown(_list, _list.size(), _itr, _states);
    }
    
    //取出最大堆的堆顶元素，放到列表未排序部分的末尾，重复此操作(n-1)次便完成了排序
    for (size_t i = 1; i < _list.size(); i++)
    {
        //将列表首项即最大值与未排序部分的末尾元素交换，注意此处是减去i
        std::iter_swap(_list.begin(), _list.end() - i);
        //让此时的堆顶向下渗流恢复，注意此处我们让渗流考虑的_size减去了i，这是防止列表末尾已经排序好的元素收到破坏
        typename std::vector<T>::iterator _top = _list.begin();
        PercolateDown(_list, _list.size() - i, _top);
    }
}

该算法的简单可视化如下，其中前半部分是将乱序列表化为最大堆的过程，后半部分则是将最大堆化为有序列表的过程

##LengthOfUnorderedList=15
##HeapSort
[0]:     14 , 2 , 5 , 12 , 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[1]:     14 , 2 , 5 , 12 ,<15>, 9 , 13 , 1 , 10 ,<3>, 8 , 6 , 7 , 4 , 11
[2]:     14 , 2 ,<13>, 12 , 15 , 9 ,<5>, 1 , 10 , 3 , 8 , 6 , 7 , 4 , 11
[3]:     14 , 2 , 13 , 12 , 15 , 9 ,<11>, 1 , 10 , 3 , 8 , 6 , 7 , 4 ,<5>
[4]:     14 ,<15>, 13 , 12 ,<2>, 9 , 11 , 1 , 10 , 3 , 8 , 6 , 7 , 4 , 5
[5]:     14 , 15 , 13 , 12 ,<8>, 9 , 11 , 1 , 10 , 3 ,<2>, 6 , 7 , 4 , 5
[6]:    <15>,<14>, 13 , 12 , 8 , 9 , 11 , 1 , 10 , 3 , 2 , 6 , 7 , 4 , 5

[7]:    <5>, 14 , 13 , 12 , 8 , 9 , 11 , 1 , 10 , 3 , 2 , 6 , 7 , 4 ,<15>
[8]:    <14>,<5>, 13 , 12 , 8 , 9 , 11 , 1 , 10 , 3 , 2 , 6 , 7 , 4 , 15
[9]:     14 ,<12>, 13 ,<5>, 8 , 9 , 11 , 1 , 10 , 3 , 2 , 6 , 7 , 4 , 15
[10]:    14 , 12 , 13 ,<10>, 8 , 9 , 11 , 1 ,<5>, 3 , 2 , 6 , 7 , 4 , 15
[11]:   <4>, 12 , 13 , 10 , 8 , 9 , 11 , 1 , 5 , 3 , 2 , 6 , 7 ,<14>, 15
[12]:   <13>, 12 ,<4>, 10 , 8 , 9 , 11 , 1 , 5 , 3 , 2 , 6 , 7 , 14 , 15
[13]:    13 , 12 ,<11>, 10 , 8 , 9 ,<4>, 1 , 5 , 3 , 2 , 6 , 7 , 14 , 15
[14]:   <7>, 12 , 11 , 10 , 8 , 9 , 4 , 1 , 5 , 3 , 2 , 6 ,<13>, 14 , 15
[15]:   <12>,<7>, 11 , 10 , 8 , 9 , 4 , 1 , 5 , 3 , 2 , 6 , 13 , 14 , 15
[16]:    12 ,<10>, 11 ,<7>, 8 , 9 , 4 , 1 , 5 , 3 , 2 , 6 , 13 , 14 , 15
[17]:   <6>, 10 , 11 , 7 , 8 , 9 , 4 , 1 , 5 , 3 , 2 ,<12>, 13 , 14 , 15
[18]:   <11>, 10 ,<6>, 7 , 8 , 9 , 4 , 1 , 5 , 3 , 2 , 12 , 13 , 14 , 15
[19]:    11 , 10 ,<9>, 7 , 8 ,<6>, 4 , 1 , 5 , 3 , 2 , 12 , 13 , 14 , 15
[20]:   <2>, 10 , 9 , 7 , 8 , 6 , 4 , 1 , 5 , 3 ,<11>, 12 , 13 , 14 , 15
[21]:   <10>,<2>, 9 , 7 , 8 , 6 , 4 , 1 , 5 , 3 , 11 , 12 , 13 , 14 , 15
[22]:    10 ,<8>, 9 , 7 ,<2>, 6 , 4 , 1 , 5 , 3 , 11 , 12 , 13 , 14 , 15
[23]:    10 , 8 , 9 , 7 ,<3>, 6 , 4 , 1 , 5 ,<2>, 11 , 12 , 13 , 14 , 15
[24]:   <2>, 8 , 9 , 7 , 3 , 6 , 4 , 1 , 5 ,<10>, 11 , 12 , 13 , 14 , 15
[25]:   <9>, 8 ,<2>, 7 , 3 , 6 , 4 , 1 , 5 , 10 , 11 , 12 , 13 , 14 , 15
[26]:    9 , 8 ,<6>, 7 , 3 ,<2>, 4 , 1 , 5 , 10 , 11 , 12 , 13 , 14 , 15
[27]:   <5>, 8 , 6 , 7 , 3 , 2 , 4 , 1 ,<9>, 10 , 11 , 12 , 13 , 14 , 15
[28]:   <8>,<5>, 6 , 7 , 3 , 2 , 4 , 1 , 9 , 10 , 11 , 12 , 13 , 14 , 15
[29]:    8 ,<7>, 6 ,<5>, 3 , 2 , 4 , 1 , 9 , 10 , 11 , 12 , 13 , 14 , 15
[30]:   <1>, 7 , 6 , 5 , 3 , 2 , 4 ,<8>, 9 , 10 , 11 , 12 , 13 , 14 , 15
[31]:   <7>,<1>, 6 , 5 , 3 , 2 , 4 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
[32]:    7 ,<5>, 6 ,<1>, 3 , 2 , 4 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
[33]:   <4>, 5 , 6 , 1 , 3 , 2 ,<7>, 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
[34]:   <6>, 5 ,<4>, 1 , 3 , 2 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
[35]:   <2>, 5 , 4 , 1 , 3 ,<6>, 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
[36]:   <5>,<2>, 4 , 1 , 3 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
[37]:    5 ,<3>, 4 , 1 ,<2>, 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
[38]:   <2>, 3 , 4 , 1 ,<5>, 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
[39]:   <4>, 3 ,<2>, 1 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
[40]:   <1>, 3 , 2 ,<4>, 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
[41]:   <3>,<1>, 2 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
[42]:   <2>, 1 ,<3>, 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
[43]:   <1>,<2>, 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15

学科笔记, 数据结构

数据结构 C++

本文由作者按照 CC BY-NC-SA 4.0 进行授权