文章

数组相关算法的浅浅刷题笔记

继续练下算法，此处是关于数组结构的一些算法题，类型涵盖双指针、哈希表、字符串、滑动窗口等

发表于 更新于
作者 WhythZ
78 分钟阅读
数组相关算法的浅浅刷题笔记

杂项

简单

只出现一次的数字

  • 数组中的全部元素的异或（同为$0$，异为$1$）运算结果即为数组中只出现一次的数字
1
2
3
4
5
6
7

int singleNumber(vector<int>& nums)
{
    int x = nums[0];
    for (int i = 1; i < nums.size(); i++)
        x ^= nums[i];
    return x;
}

多数元素

  • 排序后取中间
1
2
3
4
5

int majorityElement(vector<int>& nums)
{
    sort(nums.begin(), nums.end());
    return nums[nums.size() / 2];
}

中等

最大子数组和

  • 子数组问题通常会想到前缀和的方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

int maxSubArray(vector<int>& nums)
{
    int n = nums.size();
    if (n == 0) return 0;
    //题目规定子数组不包括空数组
    if (n == 1) return nums[0];

    //记录前缀和
    int prefix = 0;
    //记录历史最小前缀和
    int hismin = 0;
    int ans = INT_MIN;
    for (int i = 0; i < n; i++)
    {
        prefix += nums[i];
        //计算以当前前缀和减去先前的历史最小前缀和，取最大值作为答案
        ans = max(ans, prefix - hismin);
        //更新历史最小前缀和
        hismin = min(hismin, prefix);
    }
    return ans;
}
  • 动态规划的思路是，计算出的以每个元素结尾的子数组中的最大值，以新数组记录，然后遍历该新数组得出最大值即答案，问题就转化为如何找到以第$i$个元素结尾的连续子串的最值$f(i)$，动态规划转移方程如下
\[f(i) = max\{f(i - 1) + nums[i], nums[i]\}\]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

int maxSubArray(vector<int>& nums)
{
    int n = nums.size();
    if (n == 0) return 0;
    //题目规定子数组不包括空数组
    if (n == 1) return nums[0];

    //记录以nums[i]结尾的子串的最大值
    vector<int> suffix;
    suffix.resize(n);
    //特判第一个元素
    suffix[0] = nums[0];
    //在遍历过程中同时维护一个答案，这样就只需遍历一次
    int ans = suffix[0];
    for (int i = 1; i < n; i++)
    {
        suffix[i] = max(suffix[i - 1] + nums[i], nums[i]);
        ans = max(ans, suffix[i]);
    }
    return ans;
}

合并区间

  • 使用排序的思路
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

static bool CompareMin(vector<int>& _l, vector<int>& _r)
{
    return (_l[0] < _r[0]);
}

vector<vector<int>> merge(vector<vector<int>>& intervals)
{
    int n = intervals.size();
    if (n <= 1)
        return intervals;
    vector<vector<int>> ans;
    
    //按照区间左侧值大小排序，方便合并
    sort(intervals.begin(), intervals.end(), CompareMin);
    
    //一旦遇到区间左侧大于历史最大右侧值的，说明该新起一个范围了
    int lmin = intervals[0][0]; //维护区间右侧局部最小值
    int rmax = intervals[0][1]; //维护区间右侧历史最大值
    vector<int> vec;
    for (int i = 1; i < n; i++)
    {
        vec = intervals[i];

        if (vec[0] > rmax)
        {
            ans.emplace_back(vector<int>{lmin, rmax});
            //赋予新的局部左侧最小值，以及右侧历史最大值
            lmin = vec[0];
            rmax = vec[1];
        }
        else
        {
            //更新历史最大值
            if (vec[1] > rmax)
                rmax = vec[1];
        }

        //处理孤立的尾巴
        if (i == n - 1)
            ans.emplace_back(vector<int>{lmin, rmax});
    }
    return ans;
}

轮转数组

  • 借助额外的数组空间就可以轻易地解决
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

void rotate(vector<int>& nums, int k)
{
    k %= nums.size();

    std::vector<int> _temp;
    _temp.resize(k);

    for (int _j = 0; _j < k; _j++)
        _temp[_j] = nums[nums.size() - k + _j];

    for (int _i = nums.size() - k - 1; _i >= 0; _i--)
        std::swap(nums[_i], nums[k + _i]);
    
    for (int _m = 0; _m < k; _m++)
        nums[_m] = _temp[_m];
}
  • 我们还可以通过三次翻转（先整体翻转一次，再分部各翻转一次）巧妙地原地解决该问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

void rotate(vector<int>& nums, int l, int r)
{
    int mid = (r + l) / 2;
    for (int i = l; i <= mid; i++)
        swap(nums[i], nums[r - (i - l)]);
}

void rotate(vector<int>& nums, int k)
{
    int n = nums.size();
    k = k % n;
    if (k == 0) return;

    rotate(nums, 0, n - 1);
    rotate(nums, 0, k - 1);
    rotate(nums, k, n - 1);
}

除自身以外数组的乘积

  • 使用额外空间记录两组前缀积
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

vector<int> productExceptSelf(vector<int>& nums)
{
    int n = nums.size();
    vector<int> ans; ans.resize(n);

    //记录两组前缀积，特殊处理lprod头和rprod尾
    vector<int> lprod; lprod.resize(n); lprod[0] = 1;
    vector<int> rprod; rprod.resize(n); rprod[n - 1] = 1;

    int temp = 1;
    for (int i = 1; i < n; i++)
    {
        temp *= nums[i - 1];
        lprod[i] = temp;
    }
    temp = 1;
    for (int i = n - 2; i >= 0; i--)
    {
        temp *= nums[i + 1];
        rprod[i] = temp;
    }

    //计算答案
    for (int i = 0; i < n; i++)
        ans[i] = lprod[i] * rprod[i];
    return ans;
}
  • 思路依然是第i位的答案等于左右两侧乘积之积，由于乘积可以在原有数字上直接*=累积，所以可以优化掉上一个方法中的数组，只需使用双指针分别从头尾开始（同时使用两个整型分别记录历史乘积）在单次遍历中即可得出答案
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

vector<int> productExceptSelf(vector<int>& nums)
{
    int n = nums.size();
    //注意此处，以1初始化ans中的每个值，这很重要
    vector<int> ans; ans.resize(n, 1);

    int lp = 1, rp = 1, right;        
    for (int left = 0; left < n; left++)
    {
        right = (n - 1) - left;
        
        ans[left] *= lp;
        lp *= nums[left];

        ans[right] *= rp;
        rp *= nums[right];
    }
    return ans;
}

和为K的子数组

  • 暴力枚举法，高时间复杂度，低空间复杂度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

int subarraySum(vector<int>& nums, int k)
{
    int n = nums.size();

    int count = 0;
    for (int start = 0; start < n; start++)
    {
        int sum = 0;
        for (int end = start; end < n; end++)
        {
            sum += nums[end];
            if (sum == k)
                count++;
        }
    }
    return count;
}
  • 前缀和解法，该解法可类比参考路径总和III的前缀和解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

int subarraySum(vector<int>& nums, int k)
{
    int n = nums.size();
    
    //键为前缀和，值为个数
    unordered_map<int, int> hmap;
    //默认存在
    hmap[0] = 1;

    int count = 0, prefix = 0;
    for (int i = 0; i < n; i++)
    {
        prefix += nums[i];

        //检查是否存在匹配的历史前缀和，使得当前前缀和与其之差为目标值k
        //也可以直接count += hmap[prefix - k];
        if (hmap.count(prefix - k))
            count += hmap[prefix - k];
        
        //添加本轮前缀和
        //也可以直接hmap[prefix] += 1;
        if (hmap.count(prefix))
            hmap[prefix] += 1;
        else
            hmap[prefix] = 1;
    }
    return count;
}

颜色分类

  • 但是sort是快速排序，时间复杂度$O(n\ln n)$且空间复杂度$O(\ln n)$太高了
1
2
3
4

void sortColors(vector<int>& nums)
{
    sort(nums.begin(), nums.end());
}
  • 需要遍历两次，时间复杂度$O(n)$，空间复杂度$O(1)$，需锚点记录已排好的长度，类似选择排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

void sortColors(vector<int>& nums)
{
    int hook = 0;

    //将0放到左侧
    for (int i = 0; i < nums.size(); i++)
    {
        if (nums[i] == 0)
        {
            swap(nums[hook], nums[i]);
            hook++;
        }
    }

    //将1放到中间
    for (int i = hook; i < nums.size(); i++)
    {
        if (nums[i] == 1)
        {
            swap(nums[hook], nums[i]);
            hook++;
        }
    }
}
  • 双指针只需遍历一次，逻辑较为复杂，参考官方题解

下一个排列

  • 在离散数学上学过全排列，这就是其Next Permutation问题，本质上是把数组从头到尾连起来看作一个整数，找到下一个比当前数字大的最小数字
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

//把数组从头到尾连起来看作一个整数，找到下一个比当前数字大的最小数字
void nextPermutation(vector<int>& nums)
{
    //找出当前排列情况中，最靠后的一对满足的nums[i] < nums[i + 1]的相邻元素对，记录这个i
    int x = -1;
    for (int i = 0; i < nums.size() - 1; i++)
    {
        if (nums[i] < nums[i + 1])
            x = i;
    }
    //若全部降序，则不存在下一个更大的排列
    if (x == -1)
    {
        sort(nums.begin(), nums.end());
        return;
    }

    //找出nums[x]后方比它大的元素中，最小的那个
    int y = x + 1;
    for (int j = x + 1; j < nums.size(); j++)
    {
        if (nums[j] > nums[x])
            y = (nums[j] < nums[y]) ? j : y;
    }

    //将nums[x]与nums[y]互换位置，此时将nums[y]位置（即x索引位置）后方的元素排序
    swap(nums[x], nums[y]);
    sort(nums.begin() + x + 1, nums.end());
}

寻找重复数

  • 使用排序即可轻松解决，但sort修改了原数组，且快排需$O(\ln n)$空间复杂度，不符题目要求
1
2
3
4
5
6
7
8
9
10
11

int findDuplicate(vector<int>& nums)
{
    sort(nums.begin(), nums.end());
    int ans;
    for (int i = 1; i < nums.size(); i++)
    {
        if (nums[i] == nums[i - 1])
            ans = nums[i];
    }
    return ans;
}
  • 参考环形链表II中的龟兔赛跑法（判断链表是否成环并找出环入口），由于数组总共有$(n+1)$个元素，而元素值的范围$[1,n]$正好能表示除了起点$0$外的所有数组索引
    • 那么我们可以将该数组理解成一个具有元素间映射关系的一个链表，每个元素指向其元素值索引位置（类似数组实现并查集的数据结构设计）
    • 假如一个指针从$0$索引处开始沿着链表逐节点移动，必然会先后遇到重复的元素值，从最先遇到的那个元素值开始移动，最终会遇到第二个相同的元素值，相同的元素值代表与最先遇到的元素值相同的索引，即其next都是一样的，相当于这两个相同元素值指向的的next节点就是链表成环的入口，即可套用龟兔赛跑法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

int findDuplicate(vector<int>& nums)
{
    //直到相遇，说明成环
    int slow = 0, fast = 0;
    //由于一开始相等，故使用dowhile语句
    do
    {
        slow = nums[slow];
        //两倍移动速度
        //fast = nums[nums[fast]];
        fast = nums[fast];
        fast = nums[fast];
    } while (slow != fast);

    //此时相遇的点位不一定是入口，再跑一圈记录环的长度
    int length = 0;
    //由于一开始相等，故使用dowhile语句
    do
    {
        length++;
        slow = nums[slow];
    } while(slow != fast);

    //重新从起点出发，其中一个先走环的长度，让二者同速，二者必然在环入口相遇
    slow = 0; fast = 0;
    for (int i = 0; i < length; i++)
        fast = nums[fast];
    while (slow != fast)
    {
        slow = nums[slow];
        fast = nums[fast];
    }
    return slow;
}

//更优时间复杂度的写法，但更难解释
int findDuplicate(vector<int>& nums)
{
    //直到相遇，说明成环
    int slow = 0, fast = 0;
    //由于一开始相等，故使用dowhile语句
    do
    {
        slow = nums[slow];
        //两倍移动速度
        //fast = nums[nums[fast]];
        fast = nums[fast];
        fast = nums[fast];
    } while (slow != fast);
    
    //此时相遇的点位不一定是入口，将一个指针移到开头，二者等速移动必然在入口相遇
    slow = 0;
    while(slow != fast)
    {
        slow = nums[slow];
        fast = nums[fast];
    }
    return slow;
}

困难

缺失的第一个正数

  • 数组长度若为$n$，则所有可能的答案只能是$[1,n+1]$范围内的正整数，我们想到可以使用能快速查询元素的哈希表来解答，以达到$O(n)$的时间复杂度，但是这需要额外的空间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

int firstMissingPositive(vector<int>& nums)
{
    //哈希集合
    unordered_set<int> hset;
    for (int num : nums)
        hset.insert(num);

    int n = nums.size();
    for (int i = 1; i <= n; i++)
    {
        if (!hset.count(i))
            return i;
    }
    return n + 1;
}
  • 幽默题目要求原地完成，我们可以思考如何将题目提供的数组构造为类似哈希表的结构以实现同样的$O(n)$时间复杂度，参考幽默的官方题解，这题纯脑筋急转弯没啥意义
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

int firstMissingPositive(vector<int>& nums)
{
    int n = nums.size();
    for (int& num : nums)
    {
        if (num <= 0)
            num = n + 1;
    }
    for (int i = 0; i < n; i++)
    {
        int num = abs(nums[i]);
        if (num <= n)
            nums[num - 1] = -abs(nums[num - 1]);
    }
    for (int i = 0; i < n; i++)
    {
        if (nums[i] > 0)
            return i + 1;
    }
    return n + 1;
}

滑动窗口最大值

  • 最开始的思路是：随着滑动窗口每次向右移动一格，参考前一个移动窗口的最大值、队列左侧被删除的元素、队列右侧新增的元素，更新当前窗口最大值，如果左侧被丢弃的元素是原先的最大值则需重新遍历，该思路能得出正确答案，但是对于$k$很大的测试用例会超时
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

vector<int> maxSlidingWindow(vector<int>& nums, int k)
{
    if (k == 1)
        return nums;
    int n = nums.size();
    vector<int> ans;

    //维护一个最大值，如果左侧被丢弃的元素是最大值则重新更新
    int maxval = INT_MIN;
    //首次遍历初始化最大值
    for (int i = 0; i < k; i++)
        maxval = max(maxval, nums[i]);
    ans.emplace_back(maxval);

    //步进滑动窗口，维护最大值
    for (int left = 1; left <= n - k; left++)
    {
        int right = left + k - 1;

        //未冲突，则直接更新（注意left - 1表示被丢弃的元素）
        if (nums[left - 1] != maxval)
            maxval = max(maxval, nums[right]);
        else
        {
            //重新获取最大值
            maxval = INT_MIN;
            for (int i = left; i <= right; i++)
                maxval = max(maxval, nums[i]);
        }
        ans.emplace_back(maxval);
    }
    return ans;
}
  • 不难想到以空间换时间，可用优先队列（最大堆）来实时维护一系列元素中的最大值，优化掉上述解法中重新遍历的过程
    • 初始时将数组nums的前k个元素放入优先队列中，每当向右移动窗口时把新的元素放入优先队列，此时堆顶的元素就是堆中所有元素的最大值
      • 如果这个最大值并不在滑动窗口中，该值的在数组nums中的位置应当出现在滑动窗口左边界的左侧，应当将其从优先队列中移除
      • 我们没办法每次遍历时都恰好将左侧丢弃的元素剔除处最大堆，因为我们只能访问堆顶的元素，所以只能等待非窗口范围内元素冒头到堆顶的时候再将其剔除（也就是说最大堆存储的元素数量可能大于$k$个）
      • 不断地移除堆顶的元素，直到其确实出现在滑动窗口中，此时堆顶元素就是滑动窗口中的最大值，我们只需在滑动过程中重复该过程即可
    • 为了方便判断堆顶元素与滑动窗口的位置关系，可以在优先队列中存储pair<int,int>形式的二元组 (num,index)表示元素值以及元素的数组下标
    • 如此的空间复杂度$O(n)$，最大堆的单次操作耗费时间$O(\ln n)$，总时间复杂度$O(n\ln n)$
  • 引用一个神评
    • 队列中倾向于保留更年轻（索引靠后）同时还能力更强（数值更大）的对象
    • 队首能力虽最强，但一旦发现超过年龄范围（不在滑动窗口范围内）就直接开了（移除）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

vector<int> maxSlidingWindow(vector<int>& nums, int k)
{
    if (k == 1)
        return nums;
    int n = nums.size();
    vector<int> ans;

    //维护一个二元组(num,index)最大堆
    priority_queue<pair<int,int>> heap;
    //首次推送前(k-1)个元素
    for (int i = 0; i < k - 1; i++)
        heap.emplace(nums[i], i);

    //在窗口滑动过程中更新最大堆
    for (int l = 0; l <= n - k; l++)
    {
        //推送新节点
        heap.emplace(nums[l + k - 1], l + k - 1);
        //取出堆顶元素，若不在范围内则剔除
        while(heap.top().second < l)
            heap.pop();
        //存储当前窗口的实际最大值，推送完无需pop
        ans.emplace_back(heap.top().first);
    }
    return ans;
}
  • 在上述方法基础上还可以使用单调队列优化时空复杂度
    • 若当前窗口中有两个下标i和j满足$i<j$且$nums[i]\leq nums[j]$，由于需要找到滑动窗口最大值，那么当窗口向右滑动时，只要i还在窗口中，那么j一定在窗口中，故只要nums[j]存在，nums[j]必然同时存在，nums[i]一定不会是滑动窗口的最大值，故而将其从堆中永久移除也不会有问题
    • 使用一个队列存储所有还未被移除的下标（而不是元素），当滑动窗口向右移动时，不断地将新元素与队尾下标对应元素比较，若前者大于等于后者，那么队尾元素就可被永久移除
    • 不断重复此项操作直到队列为空，或新元素小于队尾的元素，这样就会保证该队列的元素值永远单调递减，此时队首下标0对应元素就是滑动窗口中的最大值，由于最大值在滑动窗口左边界的左侧，我们还需要不断从队首弹出元素，直到队首元素在窗口中为止
  • 为了可弹出队首和队尾的元素，需使用双端队列，满足单调性的双端队列一般称为单调队列
    • 时间复杂度$O(n)$：每个下标恰好被放入队列一次，最多被弹出一次
    • 空间复杂度$O(k)$：不断从队首队尾弹出元素保证了队列中最多不会超过$k+1$个元素（如果原始数组内的元素单调递减，就会在插入新元素到队尾时达到最多的$k+1$情况）
  • 再次引用神评
    • 如果新人（新插入的元素）比最邻近的老人强（比左侧的元素大），就将老人开了（移除）
    • 回到队首开除超出年龄范围（滑动窗口范围外）的老人，直到找到范围内最强（值最大）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

vector<int> maxSlidingWindow(vector<int>& nums, int k)
{
    if (k == 1)
        return nums;
    int n = nums.size();
    vector<int> ans;

    //单调队列，存储元素下标
    deque<int> q;
    //利用前(k-1)个元素初始化队列
    for (int i = 0; i < k - 1; i++)
    {
        //直到队列为空或nums[左]>=nums[右]才允许"右"下标入队
        while (!q.empty() && nums[i] >= nums[q.back()])
            q.pop_back();
        q.emplace_back(i);
    }

    //使用单调队列进行迭代
    for (int left = 0; left <= n - k; left++)
    {
        int right = left + k - 1;
        //新增对应元素值比左侧小的索引入队
        while (!q.empty() && nums[right] >= nums[q.back()])
            q.pop_back();
        q.emplace_back(right);

        //剔除超出窗口范围的索引
        while (q.front() < left)
            q.pop_front();
        ans.emplace_back(nums[q.front()]);
    }
    return ans;
}

双指针

简单

移动零

  • 暴力遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

void bubble(vector<int>& nums, int begin, int end)
{
    for (int i = begin; i < end; i++)
        std::swap(nums[i], nums[i+1]);
}

void moveZeroes(vector<int>& nums)
{
    int tail = nums.size() - 1;

    for (int i = 0; i < nums.size(); i++)
    {
        for (int j = 0; j < nums.size(); j++)
        {
            if (nums[i] == 0)
            {
                bubble(nums, i, tail);
                tail--;
            }
        }
    }
}
  • 以开辟新数组的思路（遍历nums将所有非$0$数复制到新数组，然后再想一想如何优化到使用原数组作为新数组即可），使用双指针
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

void moveZeroes(vector<int>& nums)
{
    int n = nums.size();
    int idx = 0;

    for (int i = 0; i < n; i++)
    {
        if (nums[i] != 0)
        {
            nums[idx] = nums[i];
            idx++;
        }
    }

    if (idx > n - 1)
        return;

    for (int j = idx; j < n; j++)
        nums[j] = 0;
}

中等

盛最多水的容器

  • 我第一次做的时候写出了以下错误解法，对于测试用例[1,2,4,3]它会得出错误的答案$3$而非$4$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

// int maxArea(vector<int>& height)
// {
//     //从两边夹逼，只有遇到比自身高的才会更新left或right，只需遍历一次
//     int left = 0;
//     int right = height.size() - 1;

//     //维护一个最大面积
//     int ans = 0;

//     //维护一个历史最大左侧值和历史最大右侧值（的索引）
//     int maxLIdx = left;
//     int maxRIdx = right;

//     while (left < right)
//     {
//         //更新历史局部最大值的节点
//         maxLIdx = (height[maxLIdx] < height[left]) ? left : maxLIdx;
//         maxRIdx = (height[maxRIdx] < height[right]) ? right : maxRIdx;

//         //更新最大面积，注意此处使用两者中最低的高度作为高
//         int comp = min(height[maxLIdx], height[maxRIdx]) * (maxRIdx - maxLIdx);
//         ans = max(ans, comp);

//         //继续扫描
//         left++;
//         right--;
//     }
//     return ans;
// }
  • 由于每回合的面积最大值由短板决定
    • 所以应当向内移动短板的索引，虽然如果遇到更短的板会导致面积变小，但只要一旦遇到更高的板，就有可能增加面积
    • 而如果移动长板，即使遇到了更高的板，由于短板不变，面积不可能增加，反而如果遇到了更短的短板还会导致面积丢失，所以移动长板没有任何收益
  • 我们应当在每回合都采取收益最大的操作，所以最终的解法为
    • 每回合仅将短板向内移动，直到遇到高板再更新短板为这个更高的板
    • 然后再从新高板和旧高板选出新的短板，继续将短板向内移动，重复该过程直到相遇
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

int maxArea(vector<int>& height)
{
    //从两边夹逼，只需遍历一次
    int left = 0;
    int right = height.size() - 1;

    //维护一个最大面积
    int ans = 0;

    while (left < right)
    {
        //使用短板计算新面积，更新最大面积
        int comp = (min(height[left], height[right]) * (right - left));
        ans = max(ans, comp);

        //向内移动短板
        if (height[left] < height[right])
            left++;
        else
            right--;
    }
    return ans;
}

三数之和

  • 该题是两数之和的推广，但无法套用其哈希表解法，这题关键在于去重，我们首先可以想到使用集合set<vector<int>>进行去重（此题无需使用哈希集合，并且标准库中没有vector<T>的默认哈希函数，需要手动实现才能使用unordered_set<vector<int>>）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

vector<vector<int>> threeSum(vector<int>& nums)
{
    //获取数组长度
    int n = nums.size();
    if (n < 3) return {};

    //使用集合进行去重
    set<vector<int>> ans;
    //将数组排序（升序），一是方便遍历，二是为了配合去重
    sort(nums.begin(), nums.end());

    //注意此处边界为(n - 2)，因为right从(n - 1)开始向左
    for(int i = 0; i < n - 2; i++)
    {
        int left = i + 1, right = n - 1;
        while(left < right)
        {
            //三数和太大，就将right向左移动，因为数组升序排列
            if(nums[i] + nums[left] + nums[right] > 0)
                right--;
            //三数和太小，就将left向右移动
            else if(nums[i] + nums[left] + nums[right] < 0)
                left++;
            else
            {
                ans.insert({ nums[left], nums[i], nums[right] });
                left++;
                right--;
            }
        }
    }
    return vector<vector<int>>(ans.begin(), ans.end());
}
  • 如果是[0,0,0,0,0,0,0,0]这类重复较多的用例，上述方法时间效率较低，以下方法通过对i和双指针的优化（核心是三条跳过重复元素的语句）脱离了对set的依赖，时间复杂度更低
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

vector<vector<int>> threeSum(vector<int>& nums)
{
    int n = nums.size();
    if (n < 3) return {};

    vector<vector<int>> ans;
    sort(nums.begin(), nums.end());

    for (int i = 0; i < n; i++)
    {
        //跳过重复元素
        if (i > 0 && nums[i] == nums[i - 1])
            continue;
        
        //双指针，目标是找到nums[l] + nums[r] = -nums[i]
        //只在i的右侧区域内搜索，因为i从左向右，防止从左侧产生重复
        int l = i + 1, r = n - 1;
        int target = -nums[i];
        while (l < r)
        {
            if (nums[l] + nums[r] > target)
                r--;
            else if (nums[l] + nums[r] < target) 
                l++;
            else
            {
                ans.emplace_back(vector<int>{nums[i], nums[l], nums[r]});
                l++;
                r--;
                
                //跳过重复元素
                while (l < r && nums[l] == nums[l - 1])
                    l++;
                while (l < r && nums[r] == nums[r + 1])
                    r--;
            }
        }
    }
    return ans;
}

困难

接雨水

  • 思路是找到数组中每个元素处的最大蓄水量，这取决于该点左右两个子数组中的最大高度，若两个最大高度均大于该点高度，则取其二者中的最小高度（短板效应），其与该点处高度差即为该点处的最大蓄水量，我写出了以下的超时解法
    • 从左到右遍历时，记录左侧子数组的历史最大值
    • 至于右侧子数组的最大值，则每次重新遍历计算（这也是超时的原因，可优化）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

int trap(vector<int>& height)
{
    int ans = 0;
    int n = height.size();
    if (n <= 2) return ans;

    //记录索引i左右两侧的历史最大值
    int lmax = 0, rmax = 0;
    for (int i = 0; i < n; i++)
    {
        //左侧记录历史最大值即可
        if (height[i] > lmax)
            lmax = height[i];
        
        //右侧需每次从i开始向右遍历找到最大值
        rmax = 0;
        for (int j = i; j < n; j++)
        {
            //不能记录j的起点i的值，若i右侧均小于i处高度，则右侧会漏
            if (j != i && height[j] > rmax)
                rmax = height[j];
        }
        
        //两边的最大值均找到后，计算在i处能接多少雨水，取决于两侧短板
        if (lmax > height[i] && rmax > height[i])
            ans += (lmax < rmax) ? (lmax - height[i]) : (rmax - height[i]);
        else
            ans += 0;
    }
    return ans;
}
  • 我首先想到的降低时间复杂度的思路如下，优化了寻找右侧子数组最大值的方法，该解法通过了上一个方法超时的测试用例并AC了，但在时间复杂度上仅超过了$5\%$的用户
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

int trap(vector<int>& height)
{
    int ans = 0;
    int n = height.size();
    if (n <= 2) return ans;

    //记录索引i左右两侧的历史最大值
    int lmax = 0, rmax = 0;
    //由于是从左到右遍历，故先记录全局最大值作为右侧最大值初始值
    for (int val : height)
        rmax = (val > rmax) ? val : rmax;
    //遍历过程中，左侧子数组扩容，右侧子数组减员
    for (int i = 0; i < n; i++)
    {
        //左侧记录历史最大值即可
        lmax = (height[i] > lmax) ? height[i] : lmax;
        
        //height[i]是右侧子数组在该轮丢失的元素，若其是最大值则重新获取最大值，否则无变化
        if (height[i] == rmax)
        {
            //重置为0，重新寻找右侧子数组的最大值
            rmax = 0;
            for (int j = i; j < n; j++)
            {
                //不能记录j的起点i的值，若i右侧均小于i处高度，则右侧会漏
                if (j != i && height[j] > rmax)
                    rmax = height[j];
            }
        }
        
        //两边的最大值均找到后，计算在i处能接多少雨水，取决于两侧短板
        if (lmax > height[i] && rmax > height[i])
            ans += (lmax < rmax) ? (lmax - height[i]) : (rmax - height[i]);
        else
            ans += 0;
    }
    return ans;
}
  • 考虑通过空间换时间，我们注意到前两种解法中，从左到右记录某点左侧子数组最大高度的时间复杂度很低，且只需扫描一次数组，我们是否可以从右到左也这么做呢？
  • 只需用两个数组记录每一个点的左右子数组最大高度即可，分别从左到右和从右到左扫描总共两次即可，然后最终再遍历一次计算每个点的纵向蓄水量，总共扫描三次即可得答案
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

int trap(vector<int>& height)
{
    int ans = 0;
    int n = height.size();
    if (n <= 2) return ans;

    //分别从左到右、从右到左扫描两次，记录索引i左右两侧的历史最大值
    vector<int> lmax;
    vector<int> rmax;
    lmax.resize(n);
    rmax.resize(n);
    int temp = 0;
    for (int i = 0; i < n; i++)
    {
        temp = max(height[i], temp);
        lmax[i] = temp;
    }
    temp = 0;
    for (int i = n - 1; i >= 0; i--)
    {
        temp = max(height[i], temp);
        rmax[i] = temp;
    }
    
    //最后再遍历一次计算答案
    for (int i = 0; i < n; i++)
    {
        //两边的最大值均找到后，计算在i处能接多少雨水，取决于两侧短板
        if (lmax[i] > height[i] && rmax[i] > height[i])
            ans += min(lmax[i], rmax[i]) - height[i];
        else
            ans += 0;
    }
    return ans;
}

数据流的中位数

  • 首先想到的是排序，虽然这样做的空间复杂度是$O(1)$，但会让每次新增元素都是$O(n\ln n)$级别的时间复杂度的操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class MedianFinder
{
private:
    vector<int> memory;

public:
    MedianFinder()
    {
    }
    
    void addNum(int num)
    {
        memory.emplace_back(num);
        sort(memory.begin(), memory.end());
    }
    
    double findMedian()
    {
        int n = memory.size();
        if (n % 2 == 0)
            return ((double)(memory[n / 2  - 1] + memory[n / 2]) / 2);
        else
            return memory[n / 2];
    }
};

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder* obj = new MedianFinder();
 * obj->addNum(num);
 * double param_2 = obj->findMedian();
 */
  • 所以我们考虑以空间换取更优的时间复杂度，我们记录上一次addNum时所得的中位数，然后维护一个最小堆存放大于等于该中位数的元素，维护一个最大堆存放小于该中位数的元素
    • 每当addNum新增一个元素时，放到对应容器中后检测两个容器中的元素数，更新中位数
      • 若相同，则说明总元素个数为偶数，分别取两堆堆顶取平均即为中位数
      • 若不同，则说明总元素个数为奇数，取多的那堆的堆顶作为中位数，将该元素按照规则重新放回两堆之一中，可能会与原先的不同
    • 如此便能实现每次addNum操作为$O(\ln n)$时间复杂度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

class MedianFinder
{
private:
    //中位数
    double mid;
    //最大堆，小于中位数（第二参数表示容器底层用vector维护）
    priority_queue<int, vector<int>, less<int>> lheap;
    //最小堆，大于等于中位数
    priority_queue<int, vector<int>, greater<int>> rheap;

public:
    MedianFinder()
    {
    }
    
    void addNum(int num)
    {
        //初始化
        if (lheap.empty() && rheap.empty())
        {
            mid = num;
            rheap.push(num);
            return;
        }

        //将新元素放到左边
        if (num < mid)
        {
            lheap.push(num);
            //两边均等，取平均即可
            if (lheap.size() == rheap.size())
                mid = (double)(lheap.top() + rheap.top()) / 2;
            else if (lheap.size() - rheap.size() == 1)
                mid = lheap.top();
            //否则此时左侧比右侧多两个元素，故而要转移一个到右侧，再求中位均值
            else
            {
                rheap.push(lheap.top()); lheap.pop();
                mid = (double)(lheap.top() + rheap.top()) / 2;
            }
        }
        //将新元素放到右边
        else
        {
            rheap.push(num);
            //两边均等，取平均即可
            if (lheap.size() == rheap.size())
                mid = (double)(lheap.top() + rheap.top()) / 2;
            else if (rheap.size() - lheap.size() == 1)
                mid = rheap.top();
            //否则此时右侧比左侧多两个元素，故而要转移一个到左侧，再求中位均值
            else
            {
                lheap.push(rheap.top()); rheap.pop();
                mid = (double)(lheap.top() + rheap.top()) / 2;
            }
        }
    }
    
    double findMedian()
    {
        return mid;
    }
};
  • 官方题解还有个双指针法，感觉不如上面这个方法好理解

哈希表

简单

两数之和

  • 暴力遍历
1
2
3
4
5
6
7
8
9
10
11
12

vector<int> twoSum(vector<int>& nums, int target)
{
    for (int i = 0; i < nums.size() - 1; i++)
    {
        for (int j = i + 1; j < nums.size(); j++)
        {
            if (nums[i] + nums[j] == target)
                return {i,j};
        }
    }
    return {};
}
  • 哈希表，先遍历入表再检索
1
2
3
4
5
6
7
8
9
10
11
12
13

vector<int> twoSum(vector<int>& nums, int target)
{
    unordered_map<int, int> umap;
    for (int i = 0; i < nums.size(); i++)
        umap[nums[i]] = i;
    for (int j = 0; j < nums.size(); j++)
    {
        auto pair = umap.find(target - nums[j]);
        if (pair != umap.end() && pair->second != j)
            return {j, pair->second};
    }
    return {};
}
  • 哈希表，减少了一些查询操作，时间复杂度更低
1
2
3
4
5
6
7
8
9
10
11
12

vector<int> twoSum(vector<int>& nums, int target)
{
    unordered_map<int, int> umap;
    for (int i = 0; i < nums.size(); i++)
    {
        auto pair = umap.find(target - nums[i]);
        if (pair != umap.end() && pair->second != i)
            return {i, pair->second};
        umap[nums[i]] = i;
    }
    return {};
}

中等

字母异位词分组

  • 把所有字符串排序，将排序结果作为哈希表的键
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

vector<vector<string>> groupAnagrams(vector<string>& strs)
{
    unordered_map<string, vector<string>> ht;

    for (string str : strs)
    {
        string key = str;
        sort(key.begin(), key.end());
        ht[key].emplace_back(str);
    }

    vector<vector<string>> ans;
    for (auto it = ht.begin(); it != ht.end(); it++)
        ans.emplace_back(it->second);
    return ans;
}
  • 互为字母异位词的两个字符串包含的字母相同，因此二者中相同字母出现的次数一定相同
    • 故可将每个字母出现的次数使用字符串表示，作为哈希表的键
    • 由于字符串只含小写字母，可用长度为$26$的数组记录每个字符串中每个字母的出现次数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

vector<vector<string>> groupAnagrams(vector<string>& strs)
{
    //使用匿名函数自定义对array<int,26>类型的哈希函数arrayHash
    auto arrayHash =
        //初始化捕获，变量fn被初始化为std::hash<int>的默认构造实例
        //参数列表接收一个array<int,26>的
        [fn = hash<int>{}] (const array<int, 26>& arr) -> size_t
        {
            //外层Lambda返回accumulate函数遍历数组arr的所有元素，初始哈希值为无符号整数0u
            return accumulate(arr.begin(), arr.end(), 0u,
                //
                [&](size_t acc, int num)
                {
                    //将当前累积哈希值左移1位后，与num的哈希值异或，合并为一个新的哈希值
                    return (acc << 1) ^ fn(num);
                }
            );
        };

    unordered_map<array<int, 26>, vector<string>, decltype(arrayHash)> mp(0, arrayHash);
    
    for (string& str: strs)
    {
        array<int, 26> counts{};
        int length = str.length();
        for (int i = 0; i < length; ++i)
            counts[str[i] - 'a'] ++;
        mp[counts].emplace_back(str);
    }

    //返回答案
    vector<vector<string>> ans;
    for (auto it = mp.begin(); it != mp.end(); ++it)
        ans.emplace_back(it->second);
    return ans;
}

最长连续序列

  • 最开始考虑暴力搜索，但该解法时间复杂度过高，容易超时
    • 枚举数组中的每个数$x$作为起点，不断尝试匹配$x+n$是否存在，假设最长匹配到了$x+y$，那么以$x$为起点的最长连续序列长度即为$y+1$，不断枚举并更新答案即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

bool findNum(vector<int>& nums, int target)
{
    for (int num : nums)
    {
        if (num == target)
            return true;
    }
    return false;
}

int longestConsecutive(vector<int>& nums)
{
    int maxSeq = 0;
    for (int num : nums)
    {
        int it = 1;
        int accum = 1;
        while (findNum(nums, num + it))
        {
            accum++;
            it++;
        }
        if (accum > maxSeq)
            maxSeq = accum;
    }
    return maxSeq;
}
  • 我们只需首先遍历一次将数放到哈希集合中，就可以优化每次搜索的复杂度了，但此时仍会存在极端测试用例卡超时
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

int longestConsecutive(vector<int>& nums)
{
    unordered_set<int> ht;
    for(int num : nums)
        ht.insert(num);

    int maxSeq = 0;

    for (int num : nums)
    {
        int accum = 1;
        int it = 1;
        while (ht.count(num + it))
        {
            accum++;
            it++;
        }
        if (accum > maxSeq)
            maxSeq = accum;
    }
    return maxSeq;
}
  • 我们思考继续优化，我们需要遍历每个元素查找其向上的最大连续长度，当我们遍历到每个元素的时候，可以先检测其加上当前的最大长度所得结果值是否存在于数组中，若无则跳过该数，这就省去了对那些对最大长度不可能有贡献的元素的迭代
    • 下面第一个解法是错的，因为其跳过了中间的元素，对于[9,1,4,7,3,-1,0,5,8,-1,6]测试用例，程序会在遍历到-1时（此时历史最大长度为7）直接跳过中间的1与3间的缺口，导致最终输出的答案为11而不是正确的7
    • 所以我们应当像下面的第二个解法那样，在检测到有潜力更新最大值的元素后，从头开始遍历检测而不是直接跳过
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

//第一个解法
int longestConsecutive(vector<int>& nums)
{
    if (nums.size() == 0)
        return 0;

    unordered_set<int> ht;
    for(int num : nums)
        ht.insert(num);

    int maxSeq = 1;

    for (int num : nums)
    {
        // int accum = 1;
        int accum = maxSeq;

        // int it = 1;
        int it = maxSeq;

        while (ht.count(num + it))
        {
            accum++;
            it++;
        }
        if (accum > maxSeq)
            maxSeq = accum;
    }
    return maxSeq;
}

//第二个解法
int longestConsecutive(vector<int>& nums)
{
    if (nums.size() == 0)
        return 0;

    unordered_set<int> ht;
    for(int num : nums)
        ht.insert(num);

    int maxSeq = 1;

    for (int num : nums)
    {
        int accum = 1;
        int it = 1;

        //检测当前元素num是否具有更新maxSeq的潜力
        if (ht.count(num + maxSeq))
        {
            while (ht.count(num + it))
            {
                accum++;
                it++;
            }
            if (accum > maxSeq)
                maxSeq = accum;
        }
    }
    return maxSeq;
}
  • 但即便如此还是会超时，我们再次思考优化方法，我们其实可以对有前缀元素的元素直接跳过，每次只从所有连续元素的最开头的元素开始向后遍历，只需要添加一个判断条件即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

int longestConsecutive(vector<int>& nums)
{
    if (nums.size() == 0)
        return 0;

    unordered_set<int> ht;
    for(int num : nums)
        ht.insert(num);

    int maxSeq = 1;

    for (int num : nums)
    {
        int accum = 1;
        int it = 1;
        
        //检测当前元素num是否具有更新maxSeq的潜力
        //且该元素没有前缀元素，防止可能的重复劳动
        if (ht.count(num + maxSeq) && !ht.count(num - 1))
        {
            while (ht.count(num + it))
            {
                accum++;
                it++;
            }
            if (accum > maxSeq)
                maxSeq = accum;
        }
    }
    return maxSeq;
}
  • 此时已经可以通过题目，但还有一个可以优化的点，即把第二个循环的目标改为哈希集合，而不是原数组，因为哈希集合中的元素不重复，可以减少一定的时间复杂度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

int longestConsecutive(vector<int>& nums)
{
    if (nums.size() == 0)
        return 0;

    unordered_set<int> ht;
    for(int num : nums)
        ht.insert(num);

    int maxSeq = 1;

    //去除重复元素
    //for (int num : nums)
    for (int num : ht)
    {
        int accum = 1;
        int it = 1;
        
        //检测当前元素num是否具有更新maxSeq的潜力
        //且该元素没有前缀元素，防止可能的重复劳动
        if (ht.count(num + maxSeq) && !ht.count(num - 1))
        {
            while (ht.count(num + it))
            {
                accum++;
                it++;
            }
            if (accum > maxSeq)
                maxSeq = accum;
        }
    }
    return maxSeq;
}

字符串

中等

无重复字符的最长子串

  • 我首先想到使用哈希表，得到以下实现，由于每次遇到重复元素都直接将整个窗口清空，然后再重新遍历，这样的时间复杂度较高
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

int lengthOfLongestSubstring(string s)
{
    int n = s.size();
    if (n == 0) return 0;
    int ans = 1;

    unordered_map<char, int> hmap;
    //固定left在左侧，right向右探索
    int left = 0, right = 0;
    while (right < n)
    {
        //查重
        char c = s[right];
        auto iter = hmap.find(c);
        if (iter != hmap.end())
        {
            ans = max(ans, right - left);
            left = iter->second + 1;
            right = left;
            hmap.clear();
        }
        else
        {
            //将遍历到的元素存入哈希表
            hmap[c] = right;
            right++;
            ans = max(ans, right - left);
        }
    }
    return ans;
}
  • 滑动窗口解法相当于优化了上述解法，维护了一个字符子串窗口队列
    • 将哈希表换成哈希集合，因为我们无需知晓重复元素的索引
    • 在每次遇到重复元素时，将左侧元素不断从哈希集合剔除，直到遇到与最新遍历到元素相同的节点，将其也剔除后继续下一轮遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

int lengthOfLongestSubstring(string s)
{
    int n = s.size();
    if (n == 0) return 0;
    int ans = 1;

    unordered_set<char> hset;
    //维护left在左侧，right向右探索
    int left = 0, right = 0;
    while (right < n)
    {
        //获取最新遍历到的字符
        char c = s[right];
        while (hset.find(c) != hset.end())
        {
            //移除左侧元素，直到与right位置重复的元素被移除后，跳出循环
            hset.erase(s[left]);
            left++;
        }
        //将遍历到的元素存入哈希集合
        hset.insert(c);
        //更新最大值答案
        ans = max(ans, right + 1 - left);
        //更新完答案后，继续移动右侧指针
        right++;
    }
    return ans;
}

//把最外层while循环换成for循环更简洁一点
int lengthOfLongestSubstring(string s)
{
    int n = s.size();
    if (n == 0) return 0;
    int ans = 1;

    unordered_set<char> hset;
    int left = 0;
    for (int i = 0; i < n; i++)
    {
        //获取最新遍历到的字符
        char c = s[i];
        while (hset.find(c) != hset.end())
        {
            //移除左侧元素，直到与i位置重复的元素被移除后，跳出循环
            hset.erase(s[left]);
            left++;
        }
        //将遍历到的元素存入哈希集合
        hset.insert(c);
        //更新最大值答案
        ans = max(ans, i + 1 - left);
    }
    return ans;
}

找到字符串中所有字母异位词

  • 计算目标字符串p中各个小写字母出现的次数，然后使用相同长度的窗口在s中滑动，动态维护字母出现个数，寻找符合目标的子串
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

vector<int> findAnagrams(string s, string p)
{
    int sLen = s.size(), pLen = p.size();
    vector<int> ans;

    //长度溢出
    if (sLen < pLen)
        return ans;

    //对比目标串和子窗口内，26个字母各出现的次数
    vector<int> targetCount(26, 0);
    vector<int> windowCount(26, 0);

    //先记录目标串，使用ASCII值作差
    for (char c : p)
        targetCount[c - 'a']++;
    
    //然后滑动窗口，先滑pLen个
    for (int i = 0; i < pLen; i++)
        windowCount[s[i] - 'a']++;
    if (windowCount == targetCount)
        ans.emplace_back(0);

    //继续向后滑动
    for (int i = 1; i <= sLen - pLen; i++)
    {
        windowCount[s[i - 1] - 'a']--;
        windowCount[s[i - 1 + pLen] - 'a']++;
        if (windowCount == targetCount)
            ans.emplace_back(i);
    }
    return ans;
}

最长公共子序列

  • 参考该讲解视频，可得出以下分解思路，我首先直接以递归的思路实现，不出意外超时了

最长公共子序列dp拆解.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

int longestCommonSubsequence(string text1, string text2)
{
    int n1 = text1.length(), n2 = text2.length();
    if (n1 == 0 || n2 == 0) return 0;

    //若末尾字符元素相同
    if (text1[n1 - 1] == text2[n2 - 1])
    {
        text1.pop_back(); text2.pop_back();
        return longestCommonSubsequence(text1, text2) + 1;
    }
    //若不相同
    else
    {
        string copy1 = text1, copy2 = text2;
        copy1.pop_back(); copy2.pop_back();
        return max(longestCommonSubsequence(text1, copy2),
        longestCommonSubsequence(copy1, text2));
    }
}
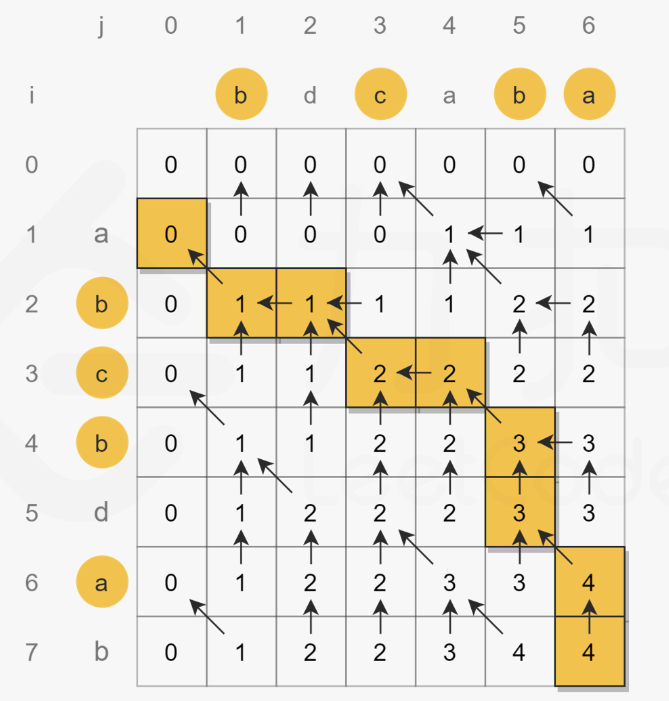
  • 因为上述方法是自上而下进行遍历的，会导致对于多个子状态重复计算（下图中的每个点都是一个子状态），我们如果自下而上进行计算，同时（使用额外矩阵空间）保存计算结果的话，就能避免重复计算带来的爆炸时间复杂度了，这就得到了二维动态规划的解法 最长公共子序列dp拆解矩阵示意.png
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

int longestCommonSubsequence(string text1, string text2)
{
    int n1 = text1.length(), n2 = text2.length();
    if (n1 == 0 || n2 == 0) return 0;

    //记录每个子状态的答案值，以text1为行，text2为列
    //字符串为空也是一个状态，故行列长度为字符个数+1
    vector<vector<int>> dp(n1 + 1, vector<int>(n2 + 1));
    //外层循环逐行进行遍历，1代表第1个字符
    for (int i = 1; i <= n1; i++)
    {
        //但获取字符的时候还是要减去1
        char c1 = text1.at(i - 1);
        //内层循环逐列遍历
        for (int j = 1; j <= n2; j++)
        {
            char c2 = text2.at(j - 1);
            //若相等
            if (c1 == c2)
                dp[i][j] = dp[i - 1][j - 1] + 1;
            //若不等
            else
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
        }
    }
    return dp[n1][n2];
}

困难

最小覆盖子串

  • 我最开始使用滑动窗口的实现如下，但是会超时，不难看出这是函数check内的循环逻辑导致的，可以针对此进行优化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

class Solution
{
public:
    unordered_map<char, int> tchars;

    bool check(const string& s, int left, int right)
    {
        unordered_map<char, int> temp = tchars;
        for (int i = left; i <= right; i++)
        {
            char c = s[i];
            if (temp.count(c))
            {
                temp[c]--;
                if (temp[c] <= 0)
                    temp.erase(c);
            }
        }
        if (temp.empty())
            return true;
        else
            return false;
    }

    string minWindow(string s, string t)
    {
        if (s.empty() || t.empty())
            return "";
        int m = s.size();

        //记录历史最短子串的相关信息
        int minLength = m, minLeft = -1;

        //记录t的字符情况
        // for (char c : t)
        // {
        //     if (tchars.count(c))
        //         tchars[c]++;
        //     else
        //         tchars[c] = 1;
        // }
        for (char c : t)
            tchars[c]++;

        //滑动窗口
        int left = 0, right = 0;
        while (right < m)
        {
            if (check(s, left, right))
            {
                //更新历史记录
                if (right - left + 1 <= minLength)
                {
                    minLength = right - left + 1;
                    minLeft = left;
                }
                left++;
            }
            else
                right++;
        }

        //获取答案，minLeft若为初始值-1而未被更行，则说明s中不存在check成功的子串窗口
        string ans = "";
        return (minLeft != -1) ? ans.append(s, minLeft, minLength) : ans;
    }
};
  • 上述的check在每轮while循环中都会被执行一次，其会遍历字符串s内的某个子串，而每轮循环中子串的长度变化均为$1$字符，这意味着会存在重复的遍历消耗性能
  • 所以我们可以再次引入一个哈希表来记忆滑动窗口中的字符，减少重复遍历，如下的实现中的check函数中也不会把tchars中的所有键值对遍历，而是遇到一个不符合条件的就直接返回false而避免无效遍历，提高时间效率
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

class Solution
{
public:
    unordered_map<char, int> tchars;
    unordered_map<char, int> window;

    bool check()
    {
        for (auto iter : tchars)
        {
            //tchars中的键必须在window中出现
            //且后者对应的值应当>=前者，但注意不是严格相等
            if (window[iter.first] < iter.second)
                return false;
        }
        return true;
    }

    string minWindow(string s, string t)
    {
        if (s.empty() || t.empty())
            return "";
        int m = s.size();

        //记录历史最短子串的相关信息
        int minLength = m, minLeft = -1;

        //记录t的字符情况
        for (char c : t)
            tchars[c]++;

        //初始化s的第一个字符
        window[s[0]]++;

        //滑动窗口
        int left = 0, right = 0;
        while (right < m)
        {
            if (check())
            {
                //更新历史记录
                if (right - left + 1 <= minLength)
                {
                    minLength = right - left + 1;
                    minLeft = left;
                }

                //更新窗口
                window[s[left]]--;
                // if (window[s[left]] == 0)
                //     window.erase(s[left]);
                left++;
            }
            else
            {
                //更新窗口
                right++;
                if (right < m) window[s[right]]++;
            }
        }

        //获取答案
        return (minLeft != -1) ? s.substr(minLeft, minLength) : "";
    }
};

最长重复子串

  • 我最开始想到的暴力解法如下，但对于某些测试用例超时了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

class Solution
{
public:
    unordered_set<string> hset;

    //针对不同长度的子串进行检测
    //只需返回所有可能重复的子串中的一个即可，以减少循环次数
    string checkByLength(const string& s, int len)
    {
        hset.clear();
        for (int i = 0; i <= s.size() - len; i++)
        {
            string str = s.substr(i, len);
            if (!hset.count(str)) hset.insert(str);
            //否则说明出现重复，直接返回
            else return str;
        }
        return "";
    }

    // //从短到长，超长测试用例用时600ms左右
    // string longestDupSubstring(string s)
    // {
    //     string ans = "";
    //     for (int i = 1; i < s.size(); i++)
    //     {
    //         //若遇到了更长的，则覆盖原来的
    //         string str = checkByLength(s, i);
    //         if (str != "") ans = str;
    //     }
    //     return ans;
    // }

    //从长到短，超长测试用例用时570ms左右
    string longestDupSubstring(string s)
    {
        //从最长往下遍历，遇到重复的直接返回即可
        for (int i = s.size() - 1; i >= 0 ; i--)
        {
            string str = checkByLength(s, i);
            if (str != "") return str;
        }
        return "";
    }
};
  • 我发现若像上面那种解法一样，按顺序（从短到长或从长到短）逐一对s的每个长度的子串调用checkByLength检测，容易造成性能浪费
  • 所以我想或许可保持checkByLength函数不变，设法降低该函数的被调用次数以降低时间复杂度，为此必然不能顺序遍历，首先想到二分查找，其核心思路是用checkByLength检测最短min和最长max子串的中间长度mid
    • 若存在mid长度的重复子串，则应当向长度区间[mid + 1, max]中寻找更长的解
    • 若不存在mid长度的重复子串，则说明不存在比mid更长长度的重复子串，因为若其存在，则这个更长的子串必然包含多个mid长度的子串，后者必然伴随符合题意，所以此时应当向长度区间[min, mid - 1]内寻求符合题意的解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

class Solution
{
public:
    unordered_set<string> hset;

    //针对不同长度的子串进行检测
    //只需返回所有可能重复的子串中的一个即可，以减少循环次数
    string checkByLength(const string& s, int len)
    {
        hset.clear();
        for (int i = 0; i <= s.size() - len; i++)
        {
            string str = s.substr(i, len);
            if (!hset.count(str)) hset.insert(str);
            //否则说明出现重复，直接返回
            else return str;
        }
        return "";
    }

    string longestDupSubstring(string s)
    {
        string result = "";
        
        //二分查找而不是顺序遍历，减少checkByLength的调用次数，以降低时间复杂度
        int left = 1, right = s.size() - 1;
        while (left <= right)
        {
            //先对中间长度mid进行检测
            int mid = (right + left) / 2;
            string dup = checkByLength(s, mid);

            //非空，说明mid长度符合条件，应向右缩小范围寻找更长的
            if (dup != "")
            {
                if (dup.size() > result.size()) result = dup;
                //在下一轮循环中，尝试寻找更长的
                left = mid + 1;
            }
            //若mid长度都不存在重复的子串，那就说明不再会有比mid更长的子串产生重复了
            //因为后者如果存在，那么mid长度必然被包含在内，必然存在mid长度的重复子串
            //故需向左缩小检测范围，避免对>mid长度进行无意义的checkByLength检测
            else
                right = mid - 1;
        }
        return result;
    }
};
  • 上述优化后的解法面对使顺序遍历方法跑出600ms的测试用例只需3ms解决，优化巨大，但面对另一个更大的用例时，不仅会超时花费350ms多，还会超出内存空间限制
    • 时间效率优化：上述二分查找实现的longestDupSubstring函数暂时难以继续优化
    • 空间效率优化：函数checkByLength使用的哈希集合大概率是导致内存超限的元凶
  • 综上考虑，应当设法优化checkByLength函数的实现以降低时空复杂度
    • 官方题解对此的解决方案是Rabin-Karp字符串编码，其表述太神秘了俺看不太懂，说白了就是用一种名为滚动哈希的特殊哈希表来代替unordered_set<string>结构
    • 原来的unordered_set<string>结构直接存储特定长度的子串本体作为元素，当子串较长时会十分占用空间，同时也会消耗更多的时间对哈希集合进行读写，而滚动哈希则是使用特殊的易检测的编码作为某长度的特定子串的唯一标识
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

class Solution
{
public:
    //使用滚动哈希代替
    string checkByLength(const string& s, int len)
    {
        if (len == 0) return "";

        const int base = 256;
        const long long mod = 1e9 + 7;
        long long hash = 0, power = 1;
        int n = s.size();

        //base^len % mod
        for (int i = 0; i < len; ++i)
            power = (power * base) % mod;

        unordered_map<long long, vector<int>> hash_map;

        //初始哈希
        for (int i = 0; i < len; ++i)
            hash = (hash * base + s[i]) % mod;
        hash_map[hash] = {0};

        for (int i = 1; i <= n - len; ++i)
        {
            //滚动计算新哈希值
            hash = (hash * base - s[i - 1] * power % mod + mod) % mod;
            hash = (hash + s[i + len - 1]) % mod;

            if (hash_map.count(hash))
            {
                for (int start : hash_map[hash])
                {
                    if (s.compare(start, len, s, i, len) == 0)
                        return s.substr(i, len);
                }
            }

            hash_map[hash].push_back(i);
        }

        return "";
    }

    string longestDupSubstring(string s)
    {
        string result = "";
        
        //二分查找而不是顺序遍历，减少checkByLength的调用次数，以降低时间复杂度
        int left = 1, right = s.size() - 1;
        while (left <= right)
        {
            //先对中间长度mid进行检测
            int mid = (right + left) / 2;
            string dup = checkByLength(s, mid);

            //非空，说明mid长度符合条件，应向右缩小范围寻找更长的
            if (dup != "")
            {
                if (dup.size() > result.size()) result = dup;
                //在下一轮循环中，尝试寻找更长的
                left = mid + 1;
            }
            //若mid长度都不存在重复的子串，那就说明不再会有比mid更长的子串产生重复了
            //因为后者如果存在，那么mid长度必然被包含在内，必然存在mid长度的重复子串
            //故需向左缩小检测范围，避免对>mid长度进行无意义的checkByLength检测
            else
                right = mid - 1;
        }
        return result;
    }
};
编程相关, 算法训练
C++
本文由作者按照 CC BY-NC-SA 4.0 进行授权