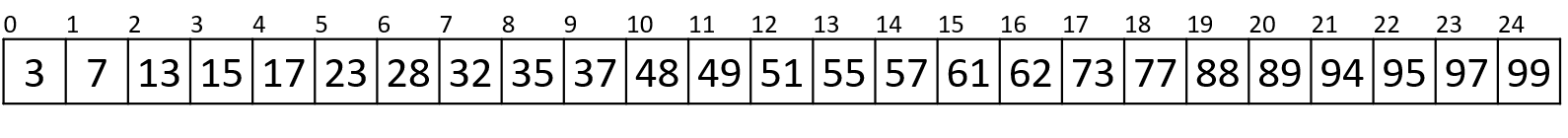快速排序的三数取中定基准方式实现

一、原理解析

1.1 算法原型

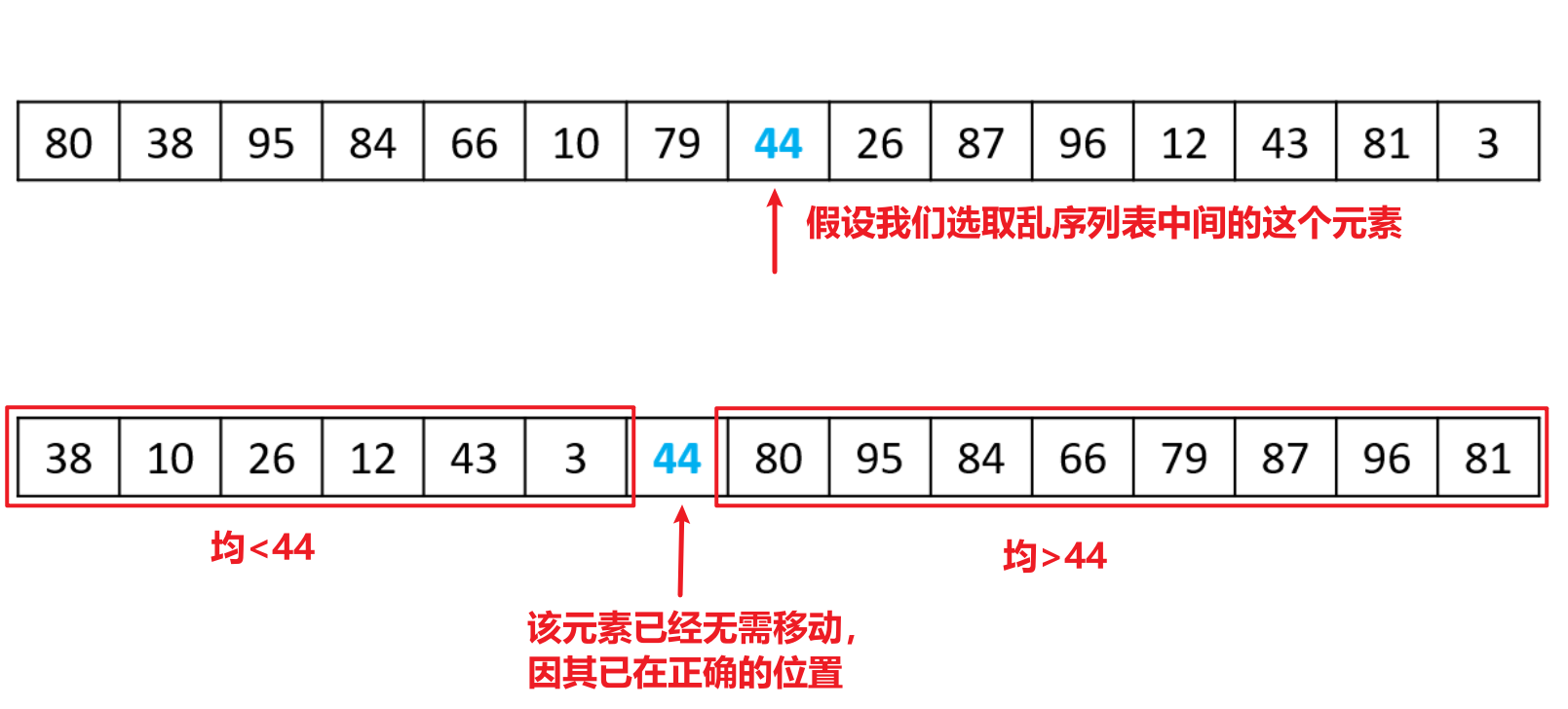
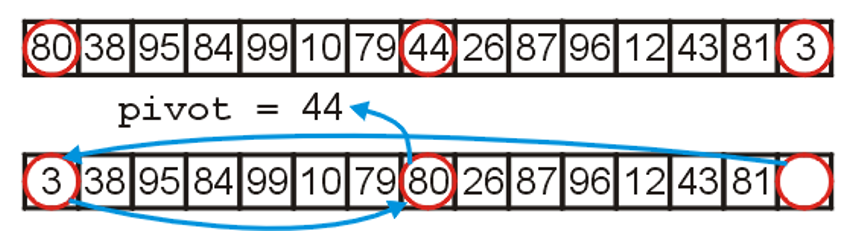
• 和归并排序一样，快速排序将乱序列表分为两个部分递归地进行排序，但不同于前者对半分，快速排序先需要选取列表中的一个元素作为基准元素（Pivot）
• 然后根据该元素的大小来将列表中剩余的元素分为两个部分（遍历剩余元素逐一与选中元素比大小），其中一部分的元素均小于选中元素，另一部分均大于，此时将选中元素放在二者中间，该元素的位置就是整个列表排好序后该元素应当在的位置（从而无需再对其进行移动）

• 如上图所示就是快速排序的一轮操作
  • 后续我们可以对左右两个部分递归地进行快速排序，直至整个列表完成排序
  • 也可以像归并排序一样设置一个子列表长度阈值，长度低于N时使用其它排序算法

1.2 基准选取策略

• 只要我们确定了基准，就可以进行一轮快速排序（上述介绍中选取了乱序列表中间的那个元素作为基准），而基准的选取策略对于算法的复杂度有着十分关键的影响
• 当我们任意选取一个基准时，最好的情况就是该基准元素是列表的中位数，此时被拨往其左侧的小于之的元素数量和大于之的元素数量就是基本相等的，若在递归的过程中保持这种最优情况，快速排序算法整体的时间复杂度就是$O(n\ln{n})$（此复杂度的计算与函数调用堆栈有关）
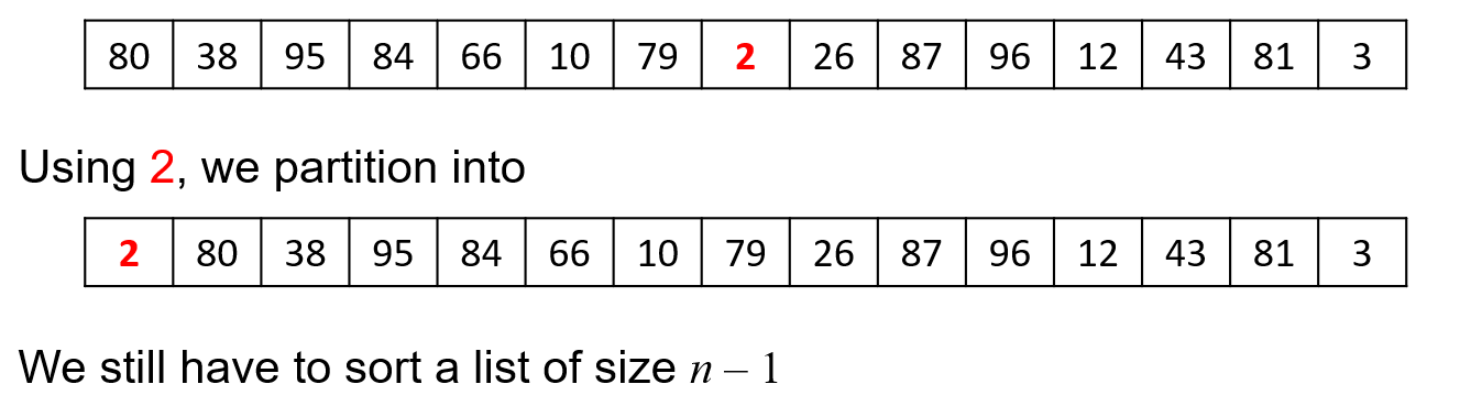
• 在此基础上，若我们没有那么幸运呢？假如我们恰好选中了列表的极值，并且在每次递归的快排中都恰好选中了极值，那么此时快排的运行过程就与选择排序的过程一致（遍历除了基准元素外的元素，将其逐一与基准比较，而基准又是极值，这就与选择排序每轮的比较过程一样了），此时快排的时间复杂度就是最坏的$O(n^2)$

• 显然我们难以确保一定能选到中位数作为基准，但我们可以通过从乱序列表的首、中、尾三个位置的元素中选择大小居中的那个作为基准元素，这样就能使得该基准相对地更加接近中位数

1.3 算法实现思路

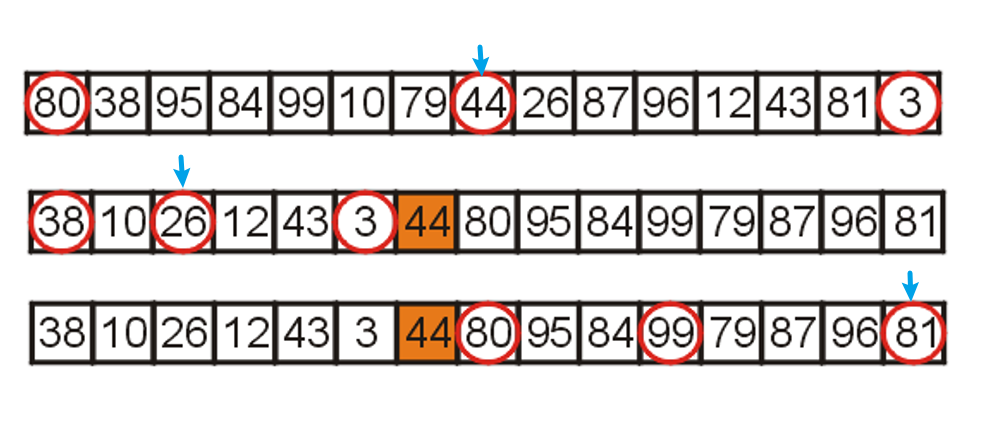
• 我们从三者中选取了中位数作为基准后，可以如下图所示（下图使用了额外的$O(n)$空间的新列表作演示）完成一轮快速排序了

• 但是由于中位数可能是三者中的任意一个，为此我们需要使用三个if来判断，为了避免这种冗杂的代码，我们进一步采取如下操作以使得三种情况能够被统一的方法处理（同时也为我们后面进行In-Place的实现做铺垫）
  • 将三者中中位的元素放入列表末尾（下图只是为了方便演示后续算法的具体实现流程而将基准元素单独拎出来，实际无需花费额外$O(1)$空间来暂存，而可以直接将其放入列表末尾）
  • 将三者中最小的元素移到列表头部位置
  • 将三者中最大的元素移到列表中部位置

• 我们回忆：每轮纯归并排序都需要额外$O(n)$的空间作为新列表来存储合并结果；而快速排序中并未使用额外内存空间，我们后续只需根据基准大小将剩余元素划为两个部分，这是In-Place的

1.4 具体实现流程

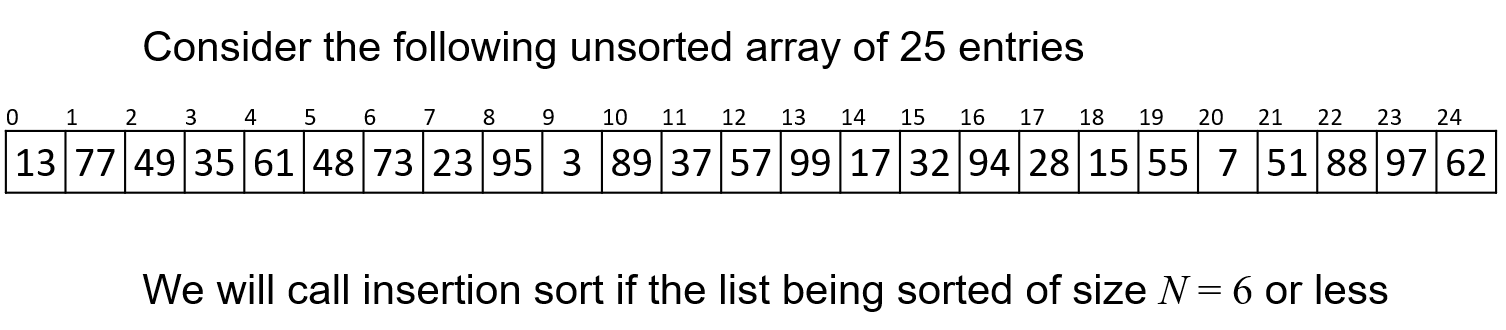
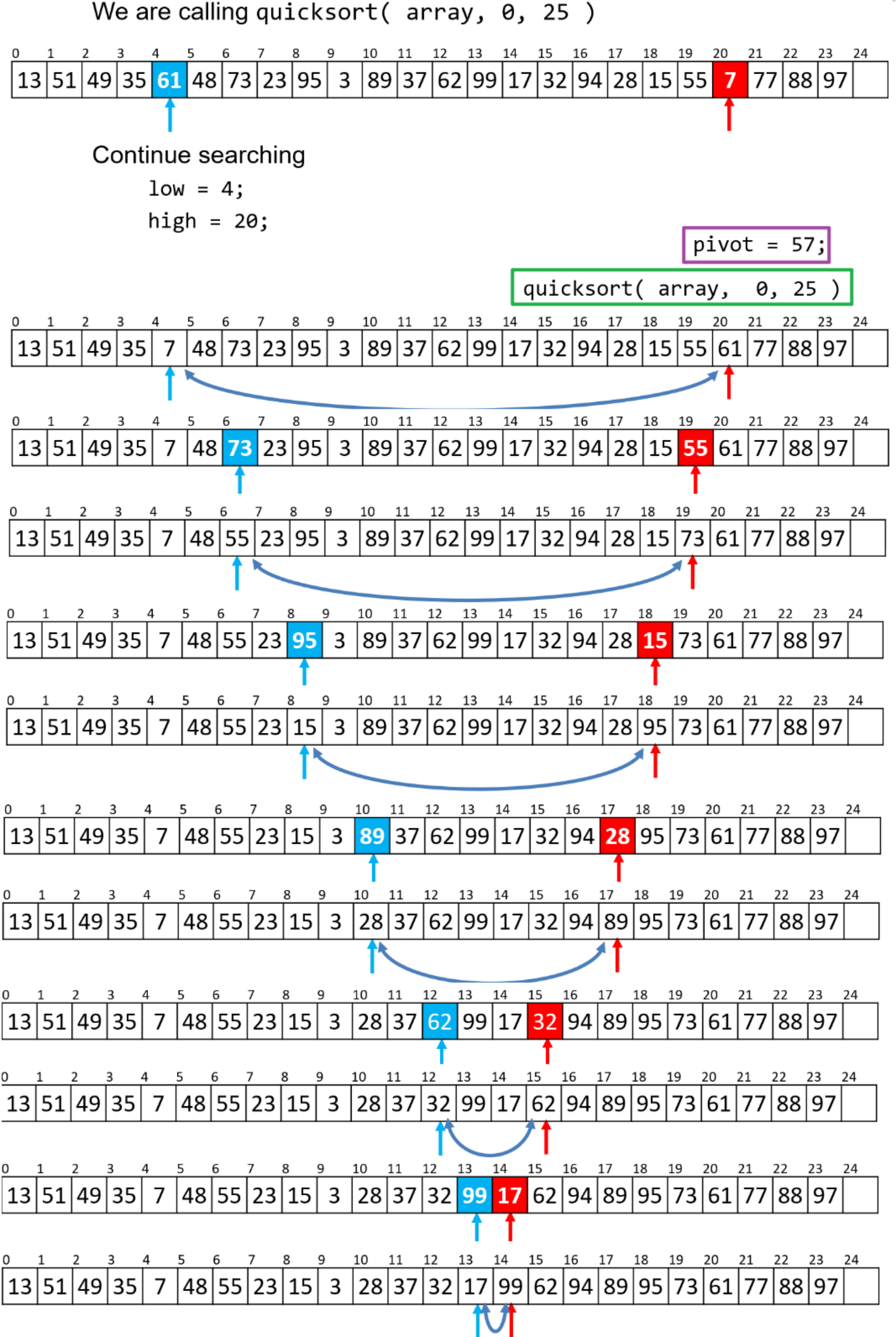
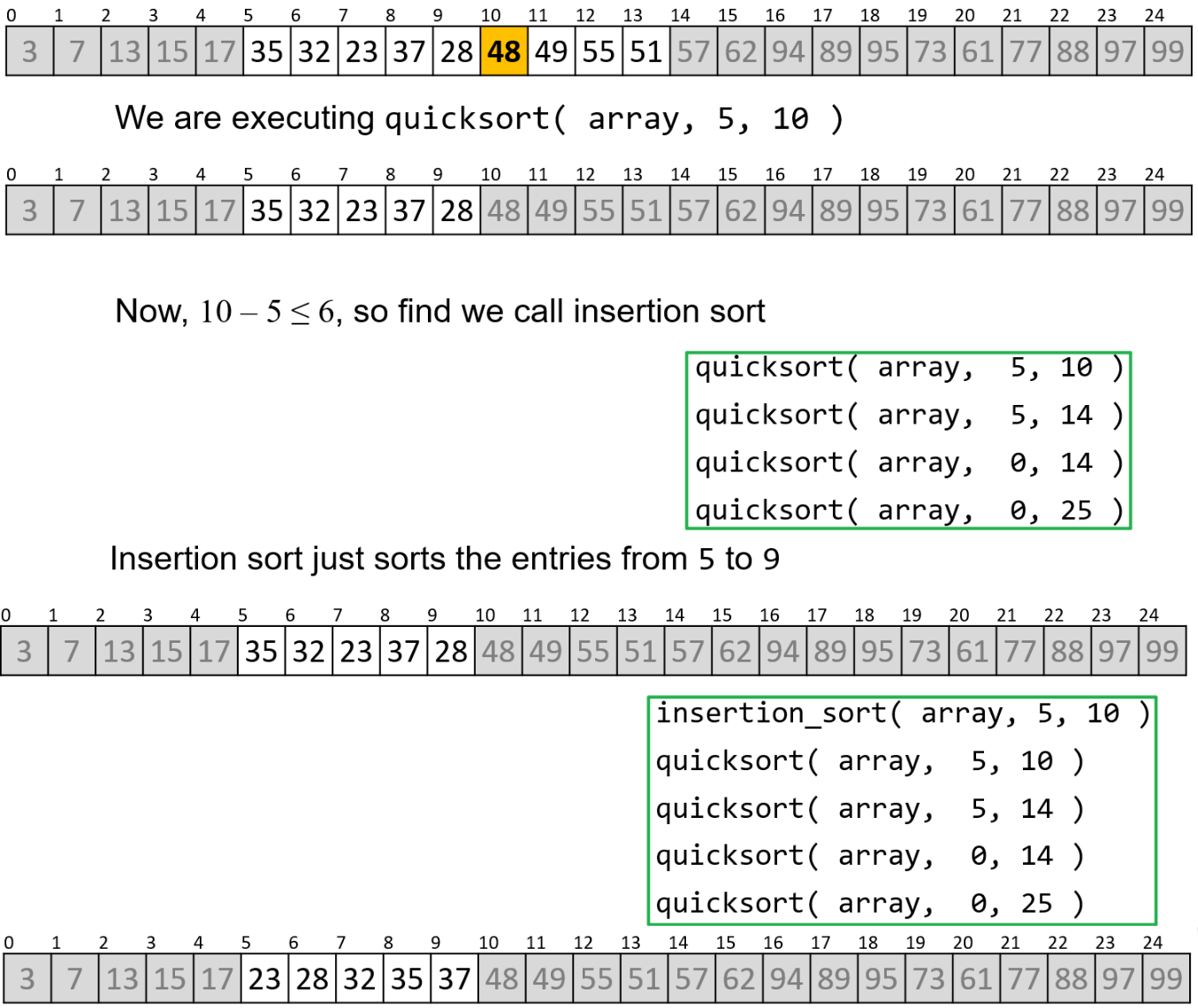
• 我们以下面这个列表为例，示意快速排序如何In-Place地进行排序，此处当子列表长度小于等于$6$时采取插入排序

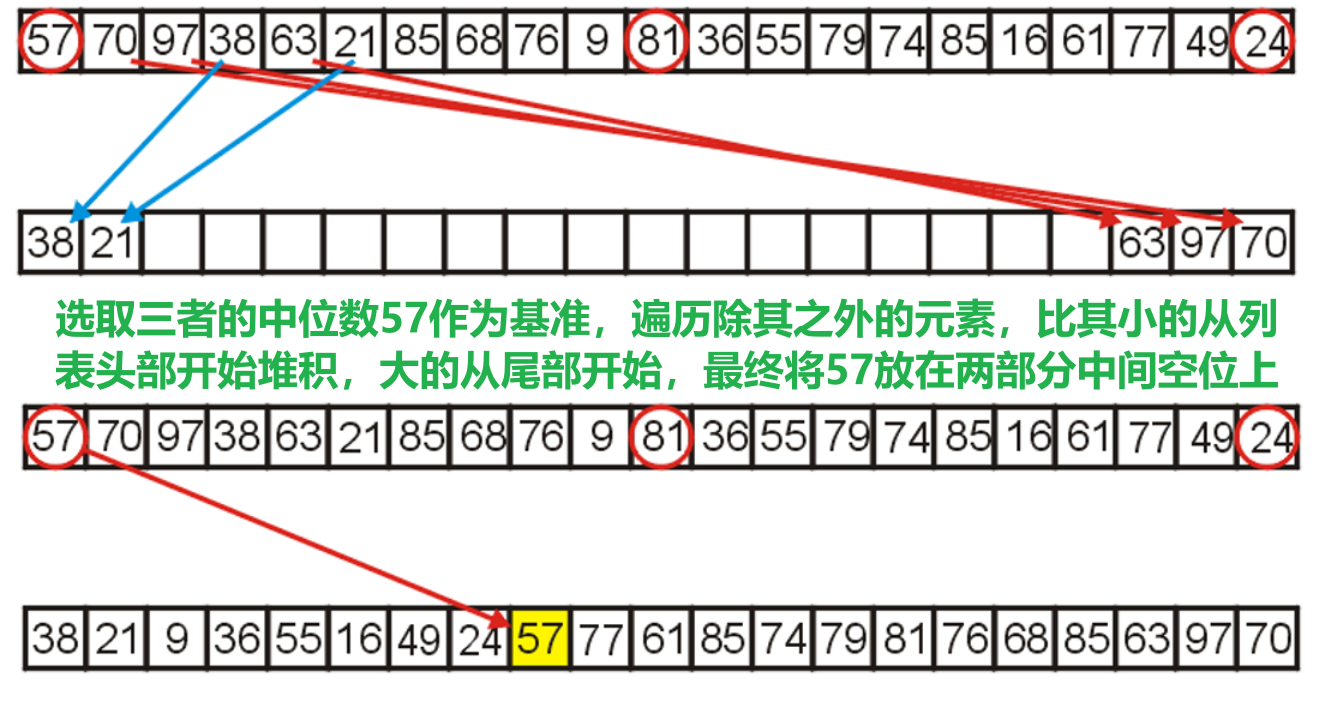
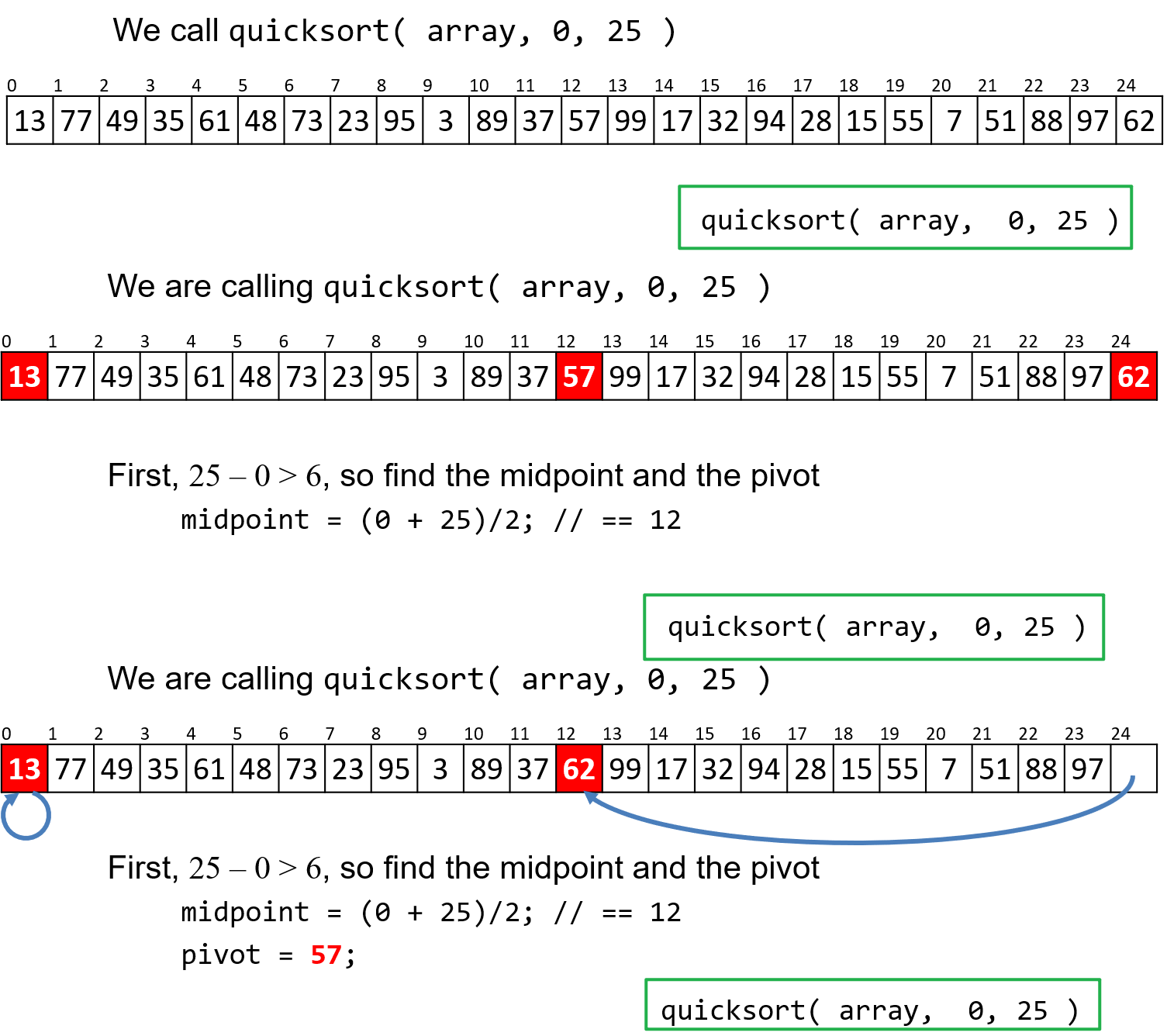
• 我们对整个列表进行快速排序的第一次调用，从三个点位的元素中选取了中位的57作为基准，并依据我们上面讲过的规则来对三者进行重新排布和存储
• 注意右下角的绿色框，那是函数调用记录（这个顺序告诉了电脑函数应当被执行的顺序，这也是需要被存储的，这也是我们最后发现即使此处的快速排序算法是In-Place的，但空间复杂度仍然平均为$O(\ln{n})$的原因）

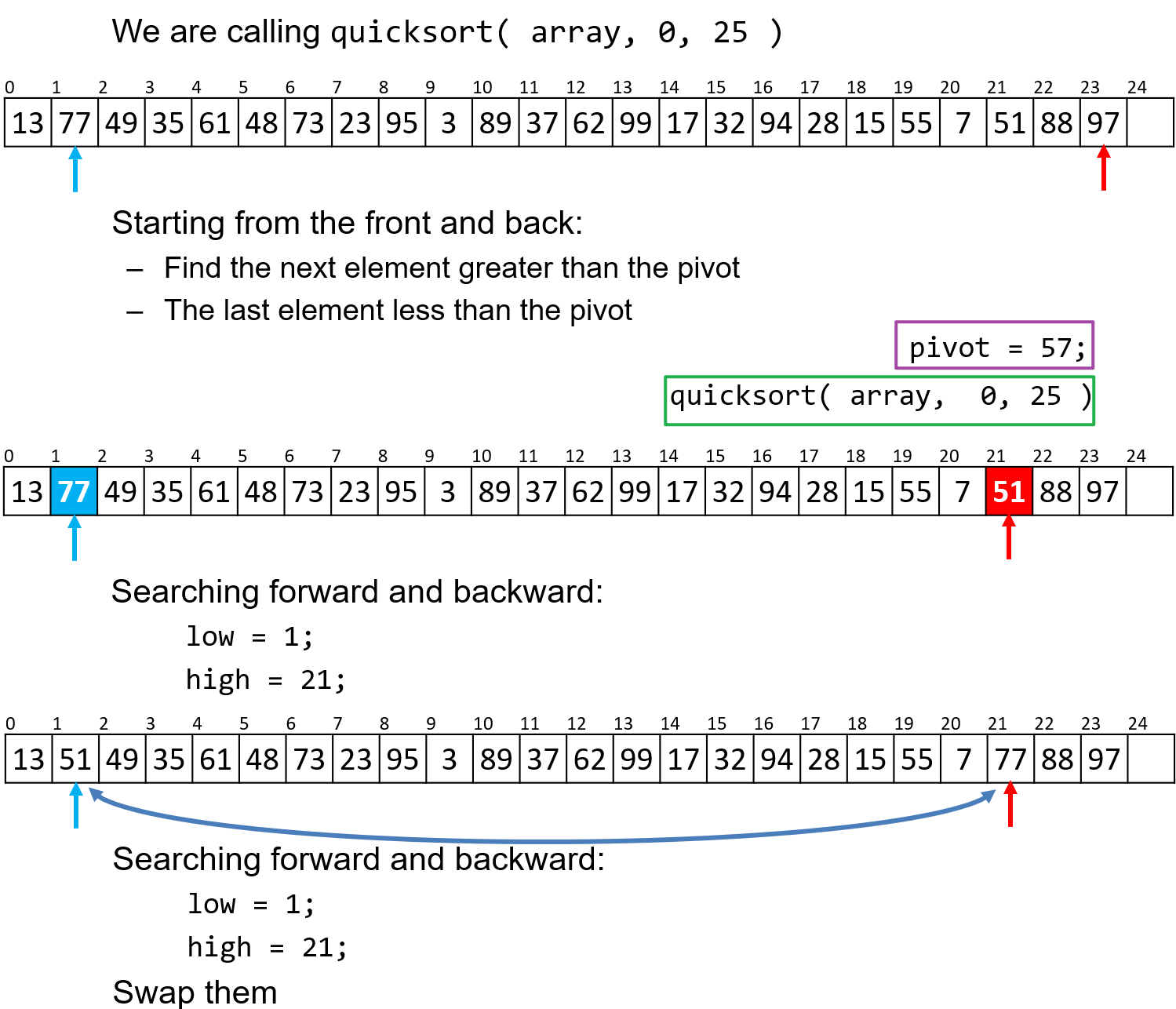
• 完成上述准备操作后，然后需要将余下元素依据与57的相对大小来分成两组
  • 选取指向列表正数和倒数第二个位置处的索引（因为已知被放到0索引处的元素一定是小于基准57的，而尾部元素是”空”的，无需让此二者与基准进行无意义的比较操作）
  • 将左侧索引向右遍历，将其指向的元素逐一与基准比较，直至找到第一个比基准57大的元素暂停遍历，此时将右侧指针向左遍历，直至找到第一个比基准小的元素暂停遍历，此时将两个索引处的元素进行对调，然后继续遍历，重复上述判断与操作

• 此时左右两侧的箭头相邻，我们就可以将右侧箭头指向的值放到列表尾部（该值是经过检验的比基准大的值），然后将基准值放入右侧箭头指向处（其实基准值就是被存储在列表末尾的，此处采用一个交换函数即可），此时这轮的基准元素57就已经处于正确的位置了

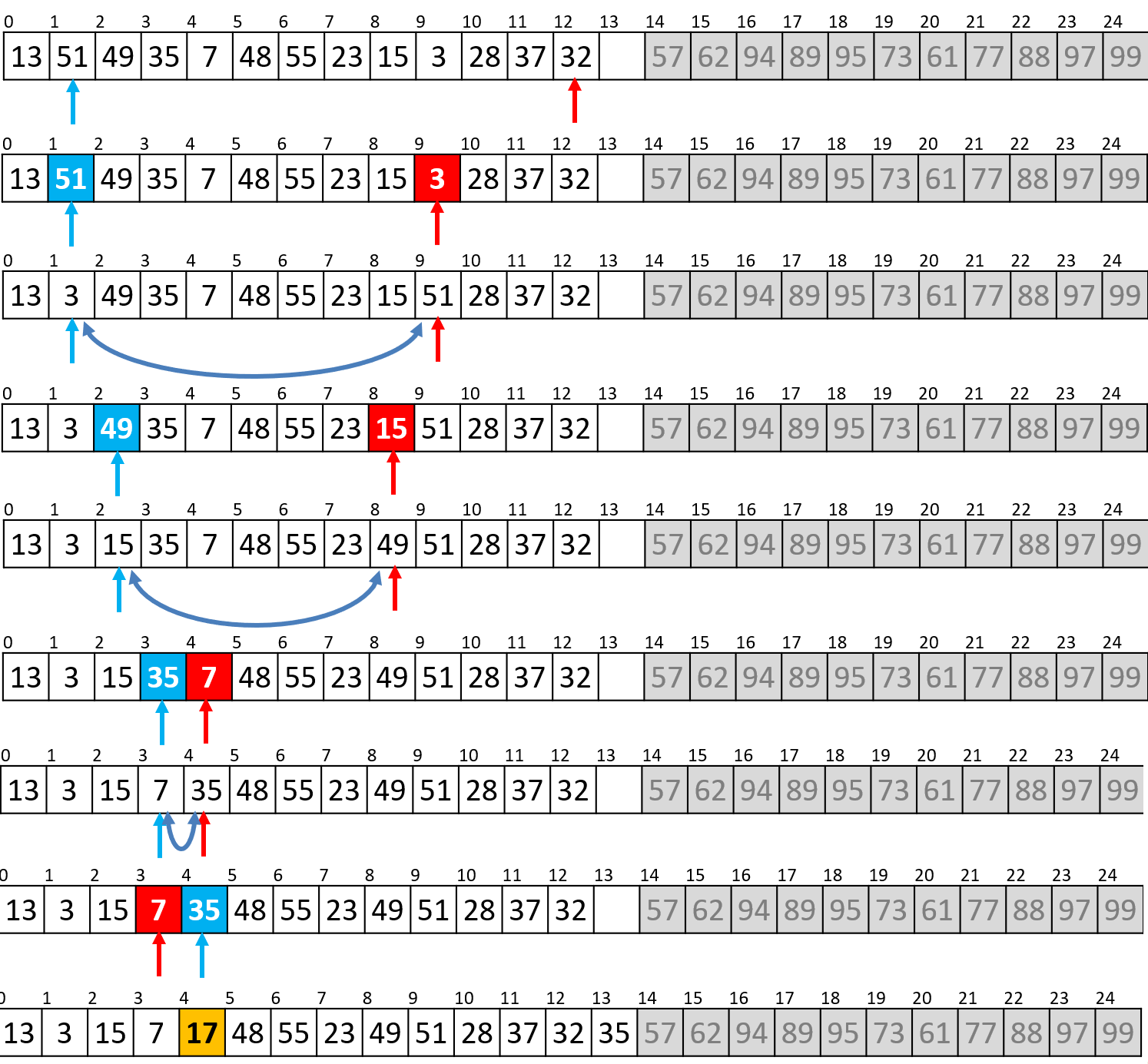
• 接下来我们便可以对57左右两侧的子列表递归地进行快速排序函数的调用了，我们先对左侧的子列表进行排序（注意右下角的绿框内的函数调用记录，这关乎后面的空间复杂度分析）

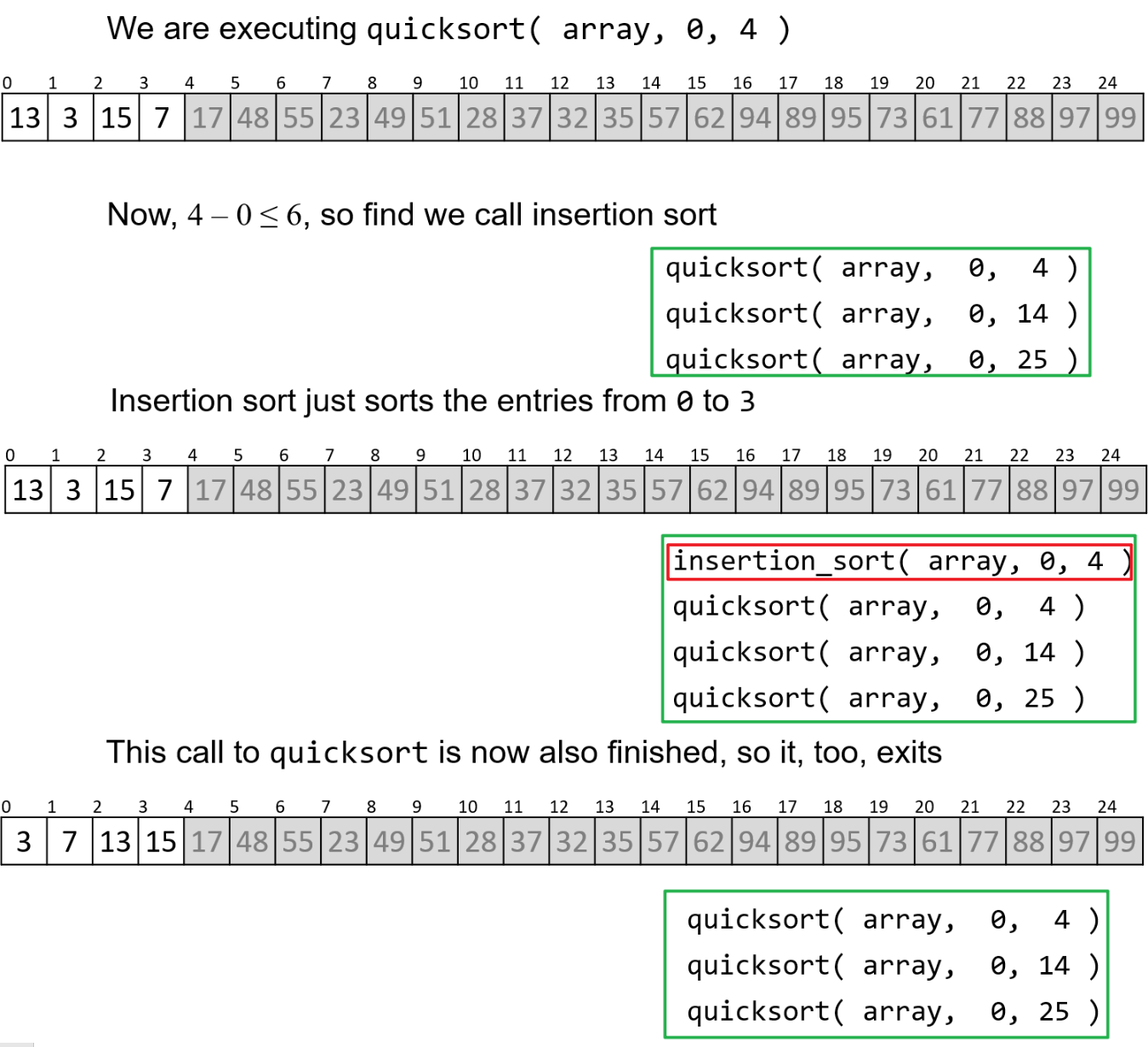
• 此时左子列表的基准17也已完成排序，可以继续递归排序左子列表的左子列表（再次留意函数调用堆栈），注意可以子列表长度小于等于$N=6$时使用插入排序

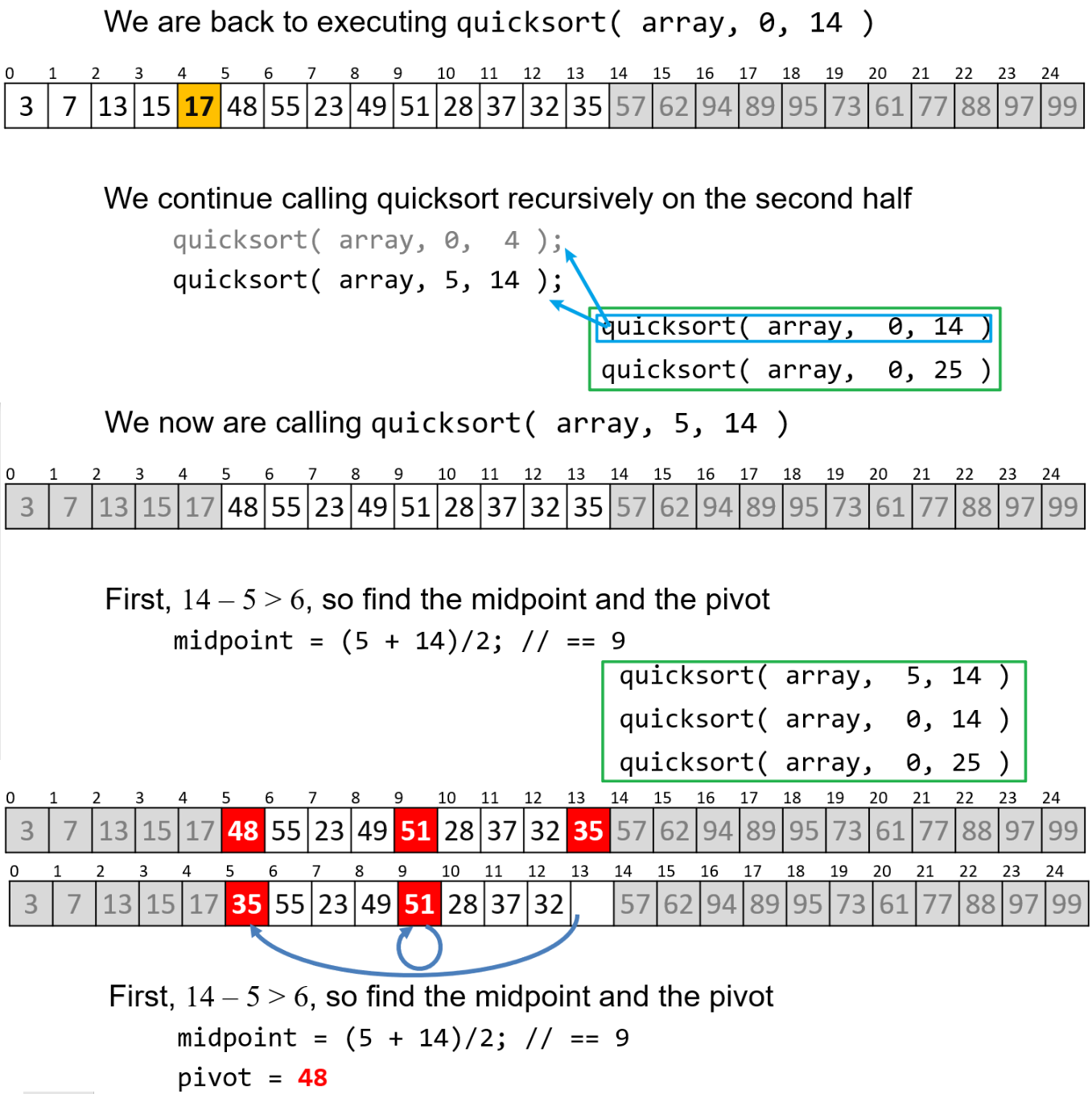
• 完成左子列表的左子列表排序后，此时函数调用堆栈最上层是对左子列表的快速排序，我们进行其下一步：对左子列表的右子列表进行快速排序

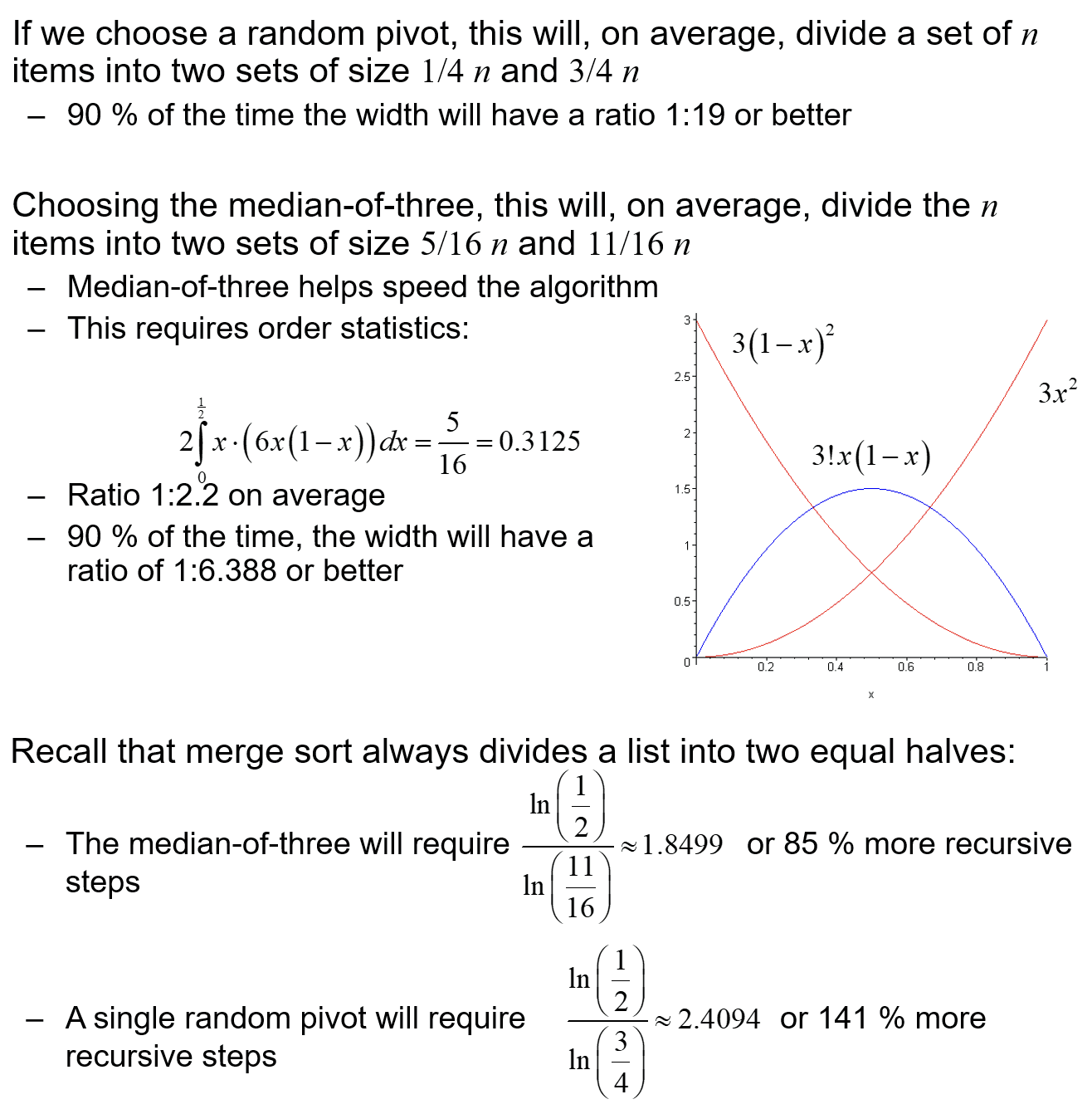
• 至此左子列表已经完成排序，我们类似地对右子列表进行递归即可完成排序

1.5 递归树

• 在上述具体的实现流程中我们可以发现一个很有意思的点：
  • 若我们把最外层的（即对列表整体调用快排时得到的）基准值当作二叉搜索树的根节点的话
  • 那么（如果我们不设置阈值N=6，而是使用完全纯粹的快速排序的话）每次递归调用快速排序函数的中间过程中得到的基准元素值，就是该二叉搜索树的（内部）节点
  • 最终递归到子列表长度为$1$时退化为的单个元素，就是该二叉搜索树的叶节点
• 我们把所有节点都换成”产生对应基准时正在调用的函数”，此时所有的函数调用记录都以其调用顺序作为大小判断依据被存储在了这颗二叉搜索树上，这棵树的高度，就等于函数调用堆栈的最大长度，所以对于长度为$n$的列表，我们就可以算出对其进行纯的快速排序时，其函数调用堆栈所需使用的空间为$O(h)=O([\log_2{n}])=O(\ln{n})$，这也就是快速排序的空间复杂度

二、复杂度分析

快速排序需要额外$O(\ln{n})$的空间，其速度比归并排序（每轮需要额外$O(n)$空间）和堆排序（需要额外$O(1)$空间）都要更快，空间占用却比归并排序小

2.1 时间复杂度

• 平均：$O(n\ln{n})$
• 最坏：$O(n^2)$

2.2 空间复杂度

• 平均：$O(\ln{n})$
  • 操作系统执行递归的程序时要对函数调用顺序进行存储，即需要使用函数调用堆栈，其长度就是递归树（就是刚介绍过的那个特殊的二搜树）的高度，所以空间复杂度为$O(\ln{n})$
  • 归并排序中也使用了递归的方法，所以其空间复杂度里也包含$O(\ln{n})$的部分，由于渐进空间复杂度只考虑最高次数的项，所以其空间复杂度最终为$O(n)$
• 最坏：$O(n)$
  • 当每次快排都选取到了极值的时候，函数调用堆栈就会很长，空间复杂度为最坏的$O(n)$，时间复杂度也是最坏的$O(n^2)$

2.3 三种排序的对比

三、代码实现

源代码以及简单的控制台可视化实现参考此处

• 先将上述介绍中将头、中、尾三个元素重新排位的方法单独实现

//从传入的三个索引中确定基准元素，并将三个元素重新置位，将基准放入第三个索引位置，最小值第一个位置，最大值第二个位置
template <typename T>
void SetPivotFromThree(std::vector<T>& _list, size_t _1Idx, size_t _2Idx, size_t _3Idx)
{
    //确保索引顺序
    if (!(_1Idx <= _2Idx && _2Idx <= _3Idx))
        throw std::runtime_error("ERROR: Incorrect order of indices when calling \"SetPivotFromThree\"");

    //确保将最小值放在第一个索引的位置
    if (_list[_2Idx] < _list[_1Idx])
        std::swap(_list[_2Idx], _list[_1Idx]);
    if (_list[_3Idx] < _list[_1Idx])
        std::swap(_list[_3Idx], _list[_1Idx]);

    //然后将剩下的两个元素比较大小，确保中位数在第三个索引位置，最大值在第二个索引位置
    if (_list[_2Idx] < _list[_3Idx])
        std::swap(_list[_2Idx], _list[_3Idx]);
}

• 然后再实现快速排序

//从列表头部、中间、尾部三个元素中选取中位数作为基准元素进行快速排序
template <typename T>
void MetaQuickSort(std::vector<T>& _list, size_t _begin, size_t _end)
{
    //计算传入部分列表的长度
    size_t _length = _end - _begin + 1;
    if (_length <= 1)
        return;
    //因为我们需要至少三个元素才能使用后面的方法进行排序，所以要单独处理两元素情况
    if (_length == 2)
    {
        if (_list[_begin] > _list[_end])
            std::swap(_list[_begin], _list[_end]);
        return;
    }
    // //可以在长度低于某阈值时使用低空间复杂度排序，如传入排序
    // if (_length <= N) { return; }
    
    //计算列表中点位置元素的索引，此变量仅在确定基准时使用一次，不影响后续实际排序时的逻辑
    size_t _mid = (_begin + _end) / 2;
    //将三者中的最小值放入列表_begin索引处，最大值放入_mid，中位数即基准元素放入_end
    SetPivotFromThree(_list, _begin, _mid, _end);
    
    //用两个索引箭头分别从第二个元素和倒数第二个元素位置开始向中间遍历
    size_t _lower = _begin + 1;
    size_t _upper = _end - 1;
    bool _flagL = false;
    bool _flagU = false;
    
    //左箭头碰到比基准大的元素，就可以暂停外部循环而进入内部循环移动右箭头寻找比基准小的元素
    while (true)
    {
        //总数为奇数个时，结束循环的条件为两索引箭头重合，偶数时则为二者大小关系颠倒
        if (_lower >= _upper)
        {
            //将基准元素放到_lower的位置
            //因为_upper递减途中可能会遇到比基准小的元素，而_lower只会停在比基准大的元素处，所以将其换到列表末尾即基准右侧是一定没问题的
            std::swap(_list[_lower], _list[_end]);
            break;
        }

        //将箭头移到两个需要被互换的位置
        if (!_flagL)
        {
            if (_list[_lower] > _list[_end])
                _flagL = true;
            else
                _lower++;
        }
        if (!_flagU)
        {
            if (_list[_upper] < _list[_end])
                _flagU = true;
            else
                _upper--;
        }

        //两个标识都为true时应当进行互换，并为下一轮循环做准备
        if (_flagL && _flagU)
        {
            std::swap(_list[_lower], _list[_upper]);
            _flagL = false;
            _flagU = false;
            _lower++;
            _upper--;
        }
    }

    //此时基准元素位于_lower索引处，对其左右两侧元素递归进行快速排序即可
    MetaQuickSort(_list, _begin, _lower - 1);
    MetaQuickSort(_list, _lower + 1, _end);
}

//快速排序
template <typename T>
void QuickSort(std::vector<T>& _list)
{
    MetaQuickSort(_list, 0, _list.size() - 1);
}

• 效果如下

##LengthOfUnorderedList=15
##QuickSort
[0]:     14 , 2 , 5 , 12 , 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[1]:    {14},{2},{5},{12},{3},{9},{13},{1},{10},{15},{8},{6},{7},{4},{11}
[2]:    <1>, 2 , 5 , 12 , 3 , 9 , 13 ,<14>, 10 , 15 , 8 , 6 , 7 , 4 ,<11>
[3]:     1 , 2 , 5 ,<4>, 3 , 9 , 13 , 14 , 10 , 15 , 8 , 6 , 7 ,<12>, 11
[4]:     1 , 2 , 5 , 4 , 3 , 9 ,<7>, 14 , 10 , 15 , 8 , 6 ,<13>, 12 , 11
[5]:     1 , 2 , 5 , 4 , 3 , 9 , 7 ,<6>, 10 , 15 , 8 ,<14>, 13 , 12 , 11
[6]:     1 , 2 , 5 , 4 , 3 , 9 , 7 , 6 , 10 ,<8>,<15>, 14 , 13 , 12 , 11
[7]:     1 , 2 , 5 , 4 , 3 , 9 , 7 , 6 , 10 , 8 ,<11>, 14 , 13 , 12 ,<15>
[8]:    {1},{2},{5},{4},{3},{9},{7},{6},{10},{8}, 11 , 14 , 13 , 12 , 15
[9]:    <1>, 2 , 5 , 4 ,<8>, 9 , 7 , 6 , 10 ,<3>, 11 , 14 , 13 , 12 , 15
[10]:    1 , 2 ,<3>, 4 , 8 , 9 , 7 , 6 , 10 ,<5>, 11 , 14 , 13 , 12 , 15
[11]:   {1},{2}, 3 , 4 , 8 , 9 , 7 , 6 , 10 , 5 , 11 , 14 , 13 , 12 , 15
[12]:    1 , 2 , 3 ,{4},{8},{9},{7},{6},{10},{5}, 11 , 14 , 13 , 12 , 15
[13]:    1 , 2 , 3 ,<4>, 8 , 9 ,<7>, 6 , 10 ,<5>, 11 , 14 , 13 , 12 , 15
[14]:    1 , 2 , 3 , 4 ,<5>, 9 , 7 , 6 , 10 ,<8>, 11 , 14 , 13 , 12 , 15
[15]:    1 , 2 , 3 ,{4}, 5 , 9 , 7 , 6 , 10 , 8 , 11 , 14 , 13 , 12 , 15
[16]:    1 , 2 , 3 , 4 , 5 ,{9},{7},{6},{10},{8}, 11 , 14 , 13 , 12 , 15
[17]:    1 , 2 , 3 , 4 , 5 ,<6>, 7 ,<9>, 10 ,<8>, 11 , 14 , 13 , 12 , 15
[18]:    1 , 2 , 3 , 4 , 5 , 6 , 7 ,<8>, 10 ,<9>, 11 , 14 , 13 , 12 , 15
[19]:    1 , 2 , 3 , 4 , 5 ,{6},{7}, 8 , 10 , 9 , 11 , 14 , 13 , 12 , 15
[20]:    1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 ,{10},{9}, 11 , 14 , 13 , 12 , 15
[21]:    1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 ,<9>,<10>, 11 , 14 , 13 , 12 , 15
[22]:    1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 ,{14},{13},{12},{15}
[23]:    1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 ,<13>,<15>, 12 ,<14>
[24]:    1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 13 ,<12>,<15>, 14
[25]:    1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 13 , 12 ,<14>,<15>
[26]:    1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 ,{13},{12}, 14 , 15
[27]:    1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 ,<12>,<13>, 14 , 15
[28]:    1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 ,{15}