归并排序的实现与思考

详细介绍归并排序的原理与C++实现，以及如何利用组合的方式谋求时间和空间复杂度间的平衡

发表于 2024/11/07 更新于 2025/01/06

作者 WhythZ

23 分钟阅读

归并排序的实现与思考

一、原理解析

1.1 算法原型

归并排序（Merge Sort）是一种分治（Divide-And-Conquer）的递归算法，当列表长度为$1$时，无需额外操作，大于$1$时则需要将列表拆分成两个子列表（总长度为偶数则对半分，奇数则分为两个长度相差为$1$的列表），然后将两个子列表分别递归调用该算法进行排序，最终通过一定的规则将所有子部分合并成为一个有序列表
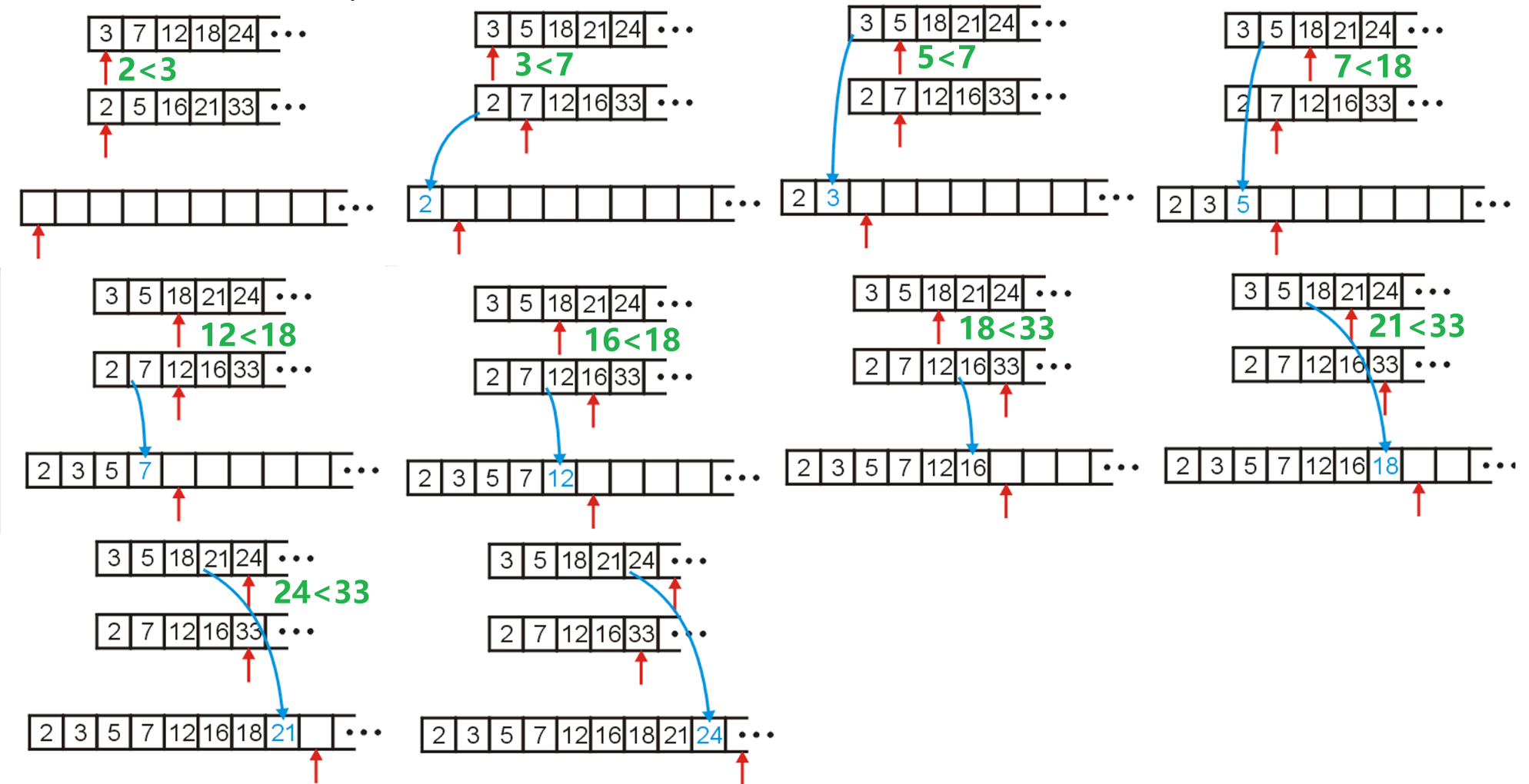
我们将两个有序列表以如下方式合并成一个大的有序列表

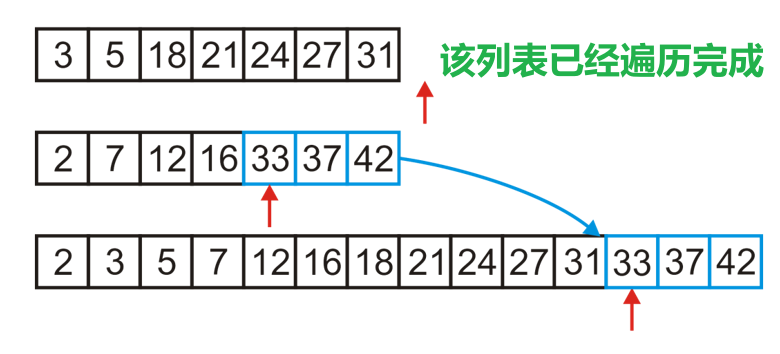
若在上述过程中其中一个有序列表遍历到底了，那么就将另一个列表的剩余部分直接放入即可

上述这种做法很快，但其缺陷就是需要使用额外$O(n)$的空间（这是非In-Place的）来存放合并后的数组，这是很难避免的，毕竟时间和空间不可能同时达到最优

1.2 弥补缺陷

既然很难减少单次合并操作占用的额外空间，那么换一下思路，我们可以减少合并操作的次数
- 回顾之前的思路：对一个乱序列表使用归并排序函数时，先将其分为两个子列表（长度相差为$0$或$1$），依次递归使用归并排序函数后，将二者通过先前所述的规则合并成为一个整体的有序列表；对于其中的递归，调用归并排序函数的列表长度为$1$时即到达递归的终点，此时便可以从底部开始向顶部层层调用合并函数，最终完成排序
- 在上述过程中：递归的终点与调用归并排序函数的子列表的长度有关，我们可以对该长度设置一定的阈值（Threshold），当调用归并排序函数的列表长度小于等于$N$时，使用另一种In-Place的排序函数（比如插入排序）以减少算法整体的空间复杂度，当大于$N$时则正常使用归并排序函数
为了以可视化的形式展示上述思路，请先接受以下假定
- 第一：我们实现了一个merge_sort(传入列表&, 子列表下界索引, 子列表上界索引)，该函数可以被递归调用实现归并排序
- 第二：我们实现了一个merge(传入列表&, 被合并的第一个列表的下界索引, 第二个列表的下界索引, 第二个列表的上界索引)，如下图所示，该函数可以按照先前规定的规则将两个排好序的列表合并成一个大的排好序的列表（因为被合并的子列表必然是相邻的关系，所以我们只需传入三个定位参数即可定位这两个子列表）

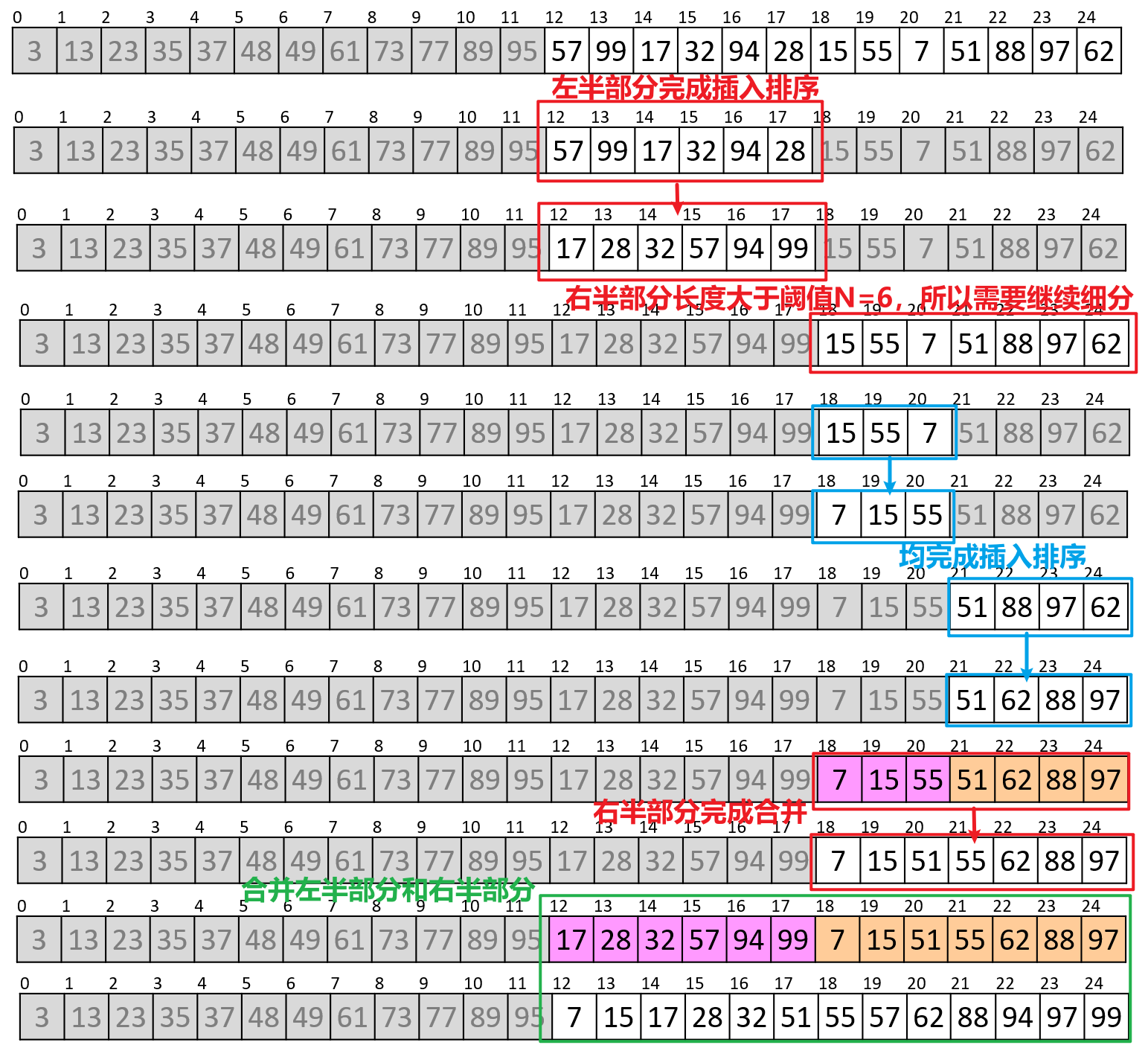
下面我们以$N=6$并使用插入排序为例，下图展示了从乱序列表开始调用归并排序，并第一次到达了使用插入排序的过程

然后我们使用插入排序对这个子列表进行排序

然后此轮递归结束，接下来就需要对上一层的下一个子列表进行归并排序，发现同样抵达阈值，那么同上理进行插入排序

此时我们再向上跳出此轮函数调用，我们就可以将这两个已经排好序的子列表调用merge函数进行合并了

我们对列表的另一半进行同样的操作流程

最终我们即可将最上层的两个有序子列表合并，此时我们就完成了排序

1.3 关联Cache的思考

在学习存储器时，我们知道Cache与主存间存在以下两种映射策略（详细内容参考详解Cache的映射策略与读写操作）
- 直接映射（Direct Mapping）：空间复杂度低（相比全相联映射），时间复杂度高（当连续取用多个指向同一Cache行的Block时会导致频繁的Miss，导致频繁的擦写）
- 全相联映射（Associative Mapping）：空间复杂度高（电路实现十分繁杂），时间复杂度低（相比直接映射）
为了使得体系的时间与空间复杂度都较为良好，衍生了组相联映射（Set Associative Mapping）这种组合的映射策略
纯粹的归并排序空间复杂度高，但时间复杂度较低；（时间复杂度为$O(n^2)$的三种排序算法中相对最好的）插入排序的时间复杂度高，但空间复杂度较低（In-Place），我们在上面的原理解析中也介绍了二者混合使用的方法，这是同样的思想
时间与空间不可兼得，所以我们往往会采用组合的方法来达到一个平衡

二、复杂度分析

在实际应用中，归并排序的速度平均一般比堆排序更快，缺点就是$O(n)$的空间复杂度

2.1 时间复杂度的理性分析

对于长度为$n$的乱序列表，对其使用纯粹的归并排序（即阈值$N=1$）的时间复杂度$T(n)$的表达式如下，其中$O(n)$是将两个子列表合并的时间复杂度

\[T(n)= \left\{ \begin{aligned} O(1)\space\space\space\space\space\space\space,\space &n=1 \\ 2T(\frac{n}{2})+O(n),\space &n>1 \end{aligned} \right .\]

根据主定理（上面的$O(n)$更严谨点应当是确界$f(n)=\Theta(n)$），可得该递归算法的时间复杂度

\[T(n)=O(n\ln{n})\]

该算法没有所谓最好或最坏的情况

2.2 时间复杂度的感性分析

为什么归并排序算法的时间复杂度不是$O(n^2)$呢？因为当我们将乱序列表拆分为两个子列表并完成子列表排序后，进行合并时我们将两个列表的首项相对比后将小的那个首项放入结果列表中，而避免了与大首项所在子列表的其余元素（都必然比该首项大）的无效比较，换句话说，此处的一次比较操作就移除了$n$（子列表长度）个逆序对

2.3 空间复杂度

每轮的渐进空间复杂度为$O(n)$
- 归并排序需要额外的$O(n)$数量级的额外空间来存放合并结果
- 归并排序递归调用时的函数调用堆栈需要$O(\ln{n})$的空间来记录调用顺序
整体的详细的非渐进空间复杂度的大小与列表长度$n$（与额外用于存放合并结果的列表所需的空间、算法函数递归调用堆栈所需的空间正相关）正相关，与阈值$N$的大小负相关

三、代码实现

源代码以及所用到的简陋的命令行可视化打印的程序参见此仓库目录

我们先看合并函数的实现

  
//传入三个索引，定位需要被融合的两个已排好序的子部分，将二者融合
template <typename T>
void Merge(std::vector<T>& _list, size_t _1Begin, size_t _2Begin, size_t _2End)
{
    //需要被合并的两个子列表必然是相邻的
    size_t _1End = _2Begin - 1;
    //分别指向两个（默认是有序的）列表中的被比较元素的索引
    size_t _1Pt = _1Begin;
    size_t _2Pt = _2Begin;

    //存放排序结果的临时列表
    std::vector<T> _result;
    
    while (true)
    {
        //当其中一个子列表被遍历完了后，跳出循环
        if (_1Pt == _1End + 1 || _2Pt == _2End + 1)
            break;
        
        //谁小放谁到结果列表里，并递增相应的索引
        if (_list[_1Pt] <= _list[_2Pt])
        {
            _result.emplace_back(_list[_1Pt]);
            _1Pt++;
        }
        else
        {
            _result.emplace_back(_list[_2Pt]);
            _2Pt++;
        }
    }

    //将另一个未被遍历完的子列表的剩余元素塞入结果列表里
    for (; _1Pt <= _1End; _1Pt++)
    {
        _result.emplace_back(_list[_1Pt]);
    }
    for (; _2Pt <= _2End; _2Pt++)
    {
        _result.emplace_back(_list[_2Pt]);
    }

    //用融合好的结果，替换掉传入列表中未融合的那部分
    for (size_t i = _1Begin; i <= _2End;i++)
    {
        _list[i] = _result[i - _1Begin];
    }
}

然后再看纯粹的归并排序实现

  
//纯粹的归并排序
template <typename T>
void MetaMergeSort(std::vector<T>& _list, size_t _begin, size_t _end)
{
    //计算需要（递归的）进行归并排序的部分的长度
    size_t _length = _end - _begin + 1;
    //单个元素无需排序
    if (_length == 1)
        return;

    //计算分裂的两个子列表的定位索引
    size_t _2Begin = _begin + _length / 2;
    size_t _1End = _begin + _length / 2 - 1;
    
    //递归调用分裂出来的左侧的子列表
    MetaMergeSort_Pure(_list, _begin, _1End);
    //递归调用分裂出来的右侧的子列表
    MetaMergeSort_Pure(_list, _2Begin, _end);

    //将上述两个排好序的子列表合并
    Merge(_list, _begin, _2Begin, _end, _states);
}

template <typename T>
void MergeSort(std::vector<T>& _list)
{
    //对整个列表进行归并排序
    MetaMergeSort_Pure(_list, 0, _list.size() - 1);
}

纯粹的归并排序其效果如下

##LengthOfUnorderedList=15
##MergeSort
[0]:     14 , 2 , 5 , 12 , 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[1]:     14 ,<0>,<0>, 12 , 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[2]:     14 ,<2>,<0>, 12 , 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[3]:     14 ,<2>,<5>, 12 , 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[4]:    <0>,<0>,<0>, 12 , 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[5]:    <2>,<0>,<0>, 12 , 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[6]:    <2>,<5>,<0>, 12 , 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[7]:    <2>,<5>,<14>, 12 , 3 , 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[8]:     2 , 5 , 14 ,<0>,<0>, 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[9]:     2 , 5 , 14 ,<3>,<0>, 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[10]:    2 , 5 , 14 ,<3>,<12>, 9 , 13 , 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[11]:    2 , 5 , 14 , 3 , 12 ,<0>,<0>, 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[12]:    2 , 5 , 14 , 3 , 12 ,<9>,<0>, 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[13]:    2 , 5 , 14 , 3 , 12 ,<9>,<13>, 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[14]:    2 , 5 , 14 ,<0>,<0>,<0>,<0>, 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[15]:    2 , 5 , 14 ,<3>,<0>,<0>,<0>, 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[16]:    2 , 5 , 14 ,<3>,<9>,<0>,<0>, 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[17]:    2 , 5 , 14 ,<3>,<9>,<12>,<0>, 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[18]:    2 , 5 , 14 ,<3>,<9>,<12>,<13>, 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[19]:   <0>,<0>,<0>,<0>,<0>,<0>,<0>, 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[20]:   <2>,<0>,<0>,<0>,<0>,<0>,<0>, 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[21]:   <2>,<3>,<0>,<0>,<0>,<0>,<0>, 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[22]:   <2>,<3>,<5>,<0>,<0>,<0>,<0>, 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[23]:   <2>,<3>,<5>,<9>,<0>,<0>,<0>, 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[24]:   <2>,<3>,<5>,<9>,<12>,<0>,<0>, 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[25]:   <2>,<3>,<5>,<9>,<12>,<13>,<0>, 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[26]:   <2>,<3>,<5>,<9>,<12>,<13>,<14>, 1 , 10 , 15 , 8 , 6 , 7 , 4 , 11
[27]:    2 , 3 , 5 , 9 , 12 , 13 , 14 ,<0>,<0>, 15 , 8 , 6 , 7 , 4 , 11
[28]:    2 , 3 , 5 , 9 , 12 , 13 , 14 ,<1>,<0>, 15 , 8 , 6 , 7 , 4 , 11
[29]:    2 , 3 , 5 , 9 , 12 , 13 , 14 ,<1>,<10>, 15 , 8 , 6 , 7 , 4 , 11
[30]:    2 , 3 , 5 , 9 , 12 , 13 , 14 , 1 , 10 ,<0>,<0>, 6 , 7 , 4 , 11
[31]:    2 , 3 , 5 , 9 , 12 , 13 , 14 , 1 , 10 ,<8>,<0>, 6 , 7 , 4 , 11
[32]:    2 , 3 , 5 , 9 , 12 , 13 , 14 , 1 , 10 ,<8>,<15>, 6 , 7 , 4 , 11
[33]:    2 , 3 , 5 , 9 , 12 , 13 , 14 ,<0>,<0>,<0>,<0>, 6 , 7 , 4 , 11
[34]:    2 , 3 , 5 , 9 , 12 , 13 , 14 ,<1>,<0>,<0>,<0>, 6 , 7 , 4 , 11
[35]:    2 , 3 , 5 , 9 , 12 , 13 , 14 ,<1>,<8>,<0>,<0>, 6 , 7 , 4 , 11
[36]:    2 , 3 , 5 , 9 , 12 , 13 , 14 ,<1>,<8>,<10>,<0>, 6 , 7 , 4 , 11
[37]:    2 , 3 , 5 , 9 , 12 , 13 , 14 ,<1>,<8>,<10>,<15>, 6 , 7 , 4 , 11
[38]:    2 , 3 , 5 , 9 , 12 , 13 , 14 , 1 , 8 , 10 , 15 ,<0>,<0>, 4 , 11
[39]:    2 , 3 , 5 , 9 , 12 , 13 , 14 , 1 , 8 , 10 , 15 ,<6>,<0>, 4 , 11
[40]:    2 , 3 , 5 , 9 , 12 , 13 , 14 , 1 , 8 , 10 , 15 ,<6>,<7>, 4 , 11
[41]:    2 , 3 , 5 , 9 , 12 , 13 , 14 , 1 , 8 , 10 , 15 , 6 , 7 ,<0>,<0>
[42]:    2 , 3 , 5 , 9 , 12 , 13 , 14 , 1 , 8 , 10 , 15 , 6 , 7 ,<4>,<0>
[43]:    2 , 3 , 5 , 9 , 12 , 13 , 14 , 1 , 8 , 10 , 15 , 6 , 7 ,<4>,<11>
[44]:    2 , 3 , 5 , 9 , 12 , 13 , 14 , 1 , 8 , 10 , 15 ,<0>,<0>,<0>,<0>
[45]:    2 , 3 , 5 , 9 , 12 , 13 , 14 , 1 , 8 , 10 , 15 ,<4>,<0>,<0>,<0>
[46]:    2 , 3 , 5 , 9 , 12 , 13 , 14 , 1 , 8 , 10 , 15 ,<4>,<6>,<0>,<0>
[47]:    2 , 3 , 5 , 9 , 12 , 13 , 14 , 1 , 8 , 10 , 15 ,<4>,<6>,<7>,<0>
[48]:    2 , 3 , 5 , 9 , 12 , 13 , 14 , 1 , 8 , 10 , 15 ,<4>,<6>,<7>,<11>
[49]:    2 , 3 , 5 , 9 , 12 , 13 , 14 ,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>
[50]:    2 , 3 , 5 , 9 , 12 , 13 , 14 ,<1>,<0>,<0>,<0>,<0>,<0>,<0>,<0>
[51]:    2 , 3 , 5 , 9 , 12 , 13 , 14 ,<1>,<4>,<0>,<0>,<0>,<0>,<0>,<0>
[52]:    2 , 3 , 5 , 9 , 12 , 13 , 14 ,<1>,<4>,<6>,<0>,<0>,<0>,<0>,<0>
[53]:    2 , 3 , 5 , 9 , 12 , 13 , 14 ,<1>,<4>,<6>,<7>,<0>,<0>,<0>,<0>
[54]:    2 , 3 , 5 , 9 , 12 , 13 , 14 ,<1>,<4>,<6>,<7>,<8>,<0>,<0>,<0>
[55]:    2 , 3 , 5 , 9 , 12 , 13 , 14 ,<1>,<4>,<6>,<7>,<8>,<10>,<0>,<0>
[56]:    2 , 3 , 5 , 9 , 12 , 13 , 14 ,<1>,<4>,<6>,<7>,<8>,<10>,<11>,<0>
[57]:    2 , 3 , 5 , 9 , 12 , 13 , 14 ,<1>,<4>,<6>,<7>,<8>,<10>,<11>,<15>
[58]:   <0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>
[59]:   <1>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>
[60]:   <1>,<2>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>
[61]:   <1>,<2>,<3>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>
[62]:   <1>,<2>,<3>,<4>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>
[63]:   <1>,<2>,<3>,<4>,<5>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>
[64]:   <1>,<2>,<3>,<4>,<5>,<6>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>
[65]:   <1>,<2>,<3>,<4>,<5>,<6>,<7>,<0>,<0>,<0>,<0>,<0>,<0>,<0>,<0>
[66]:   <1>,<2>,<3>,<4>,<5>,<6>,<7>,<8>,<0>,<0>,<0>,<0>,<0>,<0>,<0>
[67]:   <1>,<2>,<3>,<4>,<5>,<6>,<7>,<8>,<9>,<0>,<0>,<0>,<0>,<0>,<0>
[68]:   <1>,<2>,<3>,<4>,<5>,<6>,<7>,<8>,<9>,<10>,<0>,<0>,<0>,<0>,<0>
[69]:   <1>,<2>,<3>,<4>,<5>,<6>,<7>,<8>,<9>,<10>,<11>,<0>,<0>,<0>,<0>
[70]:   <1>,<2>,<3>,<4>,<5>,<6>,<7>,<8>,<9>,<10>,<11>,<12>,<0>,<0>,<0>
[71]:   <1>,<2>,<3>,<4>,<5>,<6>,<7>,<8>,<9>,<10>,<11>,<12>,<13>,<0>,<0>
[72]:   <1>,<2>,<3>,<4>,<5>,<6>,<7>,<8>,<9>,<10>,<11>,<12>,<13>,<14>,<0>
[73]:   <1>,<2>,<3>,<4>,<5>,<6>,<7>,<8>,<9>,<10>,<11>,<12>,<13>,<14>,<15>

然后再看融合了插入排序的归并排序方法

  
//当子列表的长度小于等于该值时，调用其它的低空间复杂度的排序函数（此处使用插入排序）以降低归并排序的空间复杂度
#define MERGE_SORT_MIX_THRESHOLD 6
template <typename T>
void MERGE_SORT_MIX_BORROW(std::vector<T>& _list, size_t _begin, size_t _end)
{
    for (size_t i = _begin + 1; i <= _end; i++)
    {
        //将i索引处的值向左浮动至符合顺序的位置进行"插入"
        size_t _idx = i;
        while (_list[_idx - 1] > _list[_idx])
        {
            //注意此处要限制_idx的下界，不能超出划定的范围
            if (_idx <= _begin)
                break;
            std::swap(_list[_idx - 1], _list[_idx]);
            _idx--;
        }
    }
}

template <typename T>
void MetaMergeSort_Mix(std::vector<T>& _list, size_t _begin, size_t _end)
{
    //计算需要（递归的）进行归并排序的部分的长度
    size_t _length = _end - _begin + 1;
    //单个元素无需排序
    if (_length == 1)
        return;

    //计算分裂的两个子列表的定位索引
    size_t _2Begin = _begin + _length / 2;
    size_t _1End = _begin + _length / 2 - 1;

    //若保留此判断，则就不是纯粹的归并排序了，若不包含则就是纯粹的归并排序
    if (_length <= MERGE_SORT_MIX_THRESHOLD)
    {
        //若子列表长度小于等于预定的阈值，则对该子列表调用其它低空间复杂度的排序函数
        MERGE_SORT_MIX_BORROW(_list, _begin, _end);
        return;
    }
    
    //递归调用分裂出来的左侧的子列表
    MetaMergeSort_Mix(_list, _begin, _1End);
    //递归调用分裂出来的右侧的子列表
    MetaMergeSort_Mix(_list, _2Begin, _end);

    //将上述两个排好序的子列表合并
    Merge(_list, _begin, _2Begin, _end);
}

学科笔记, 数据结构

本文由作者按照 CC BY-NC-SA 4.0 进行授权