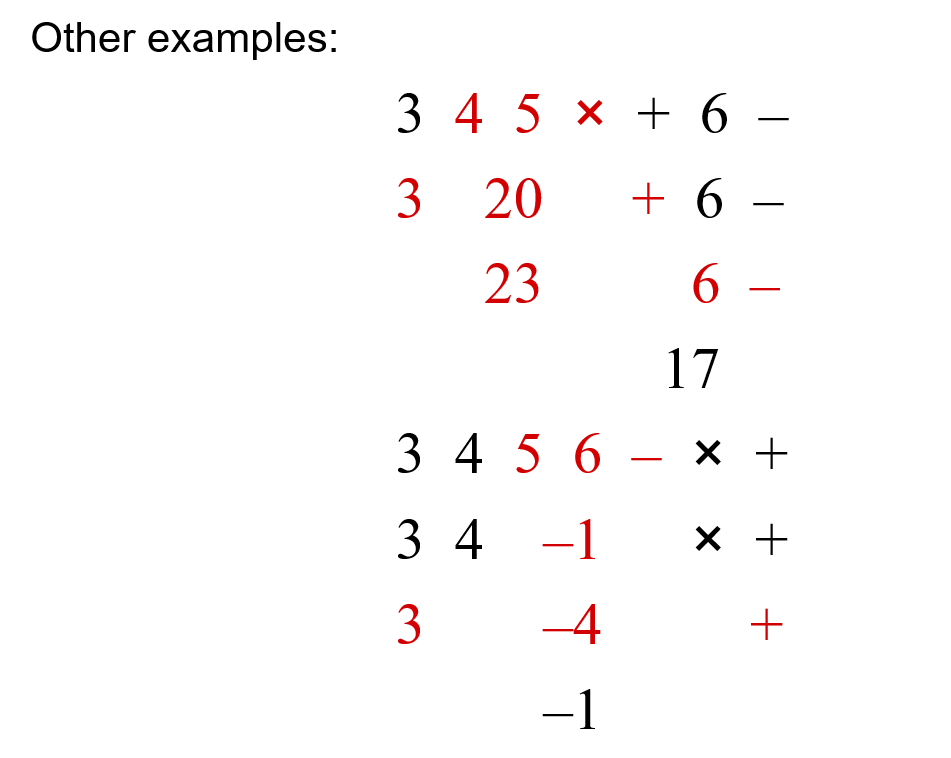常见线性表结构分析及其实现

此篇博客是关于我在数据结构学习过程中，用无STL的C++进行简单实现的常见线性表及其分析笔记

发表于 2024/09/09 更新于 2025/01/05

作者 WhythZ

25 分钟阅读

常见线性表结构分析及其实现

具体代码的实现参考我的项目仓库，我将每种线性表结构的实现分别封装在对应的.hpp头文件内，你只需要在Main.cpp的main()函数内调用相关的测试函数并运行即可查看调试信息

一、关于线性表

1.1 定义与性质

线性表（List）是具有相同特性数据元素的有限序列（Finite Sequence）
- 顺序存储结构列表（Sequential List）如数组（Array）
- 链式存储结构列表（Linked List）即链表
如下所示的就是线性表
- $n$为元素总个数即表长，$n=0$时该表是空表（Empty List）
- $a_1$为起始节点，$a_n$为终端节点，二者中间的均为数据元素
- $a_{i-1}$是$a_i$的直接前驱（Predecessor），$a_{i+1}$是$a_i$的直接后继（Successor）

\[a_1,a_2,...,a_{i-1},a_i,a_{i+1},...,a_n\]

1.2 应用案例

用顺序存储结构的线性表表示一个多项式（Polynomial）的例子如下

上图这种记录方式在项数少的时候没问题，但是对于如下这种稀疏多项式来说，由于要存储大量的无意义的零值，会浪费很多空间

\[S(x) = 2 + 5x^{10000} + 3x^{20000}\]

我们可以采用只记录非零项的方式来解决这个问题，如我们用此线性表表示上面这个多项式

\[P = ((2, 0), (5, 10000), (3, 20000))\]

两个采取这种表示形式的多项式的相加只需新建一个空线性表，然后从最小次数项开始依次往上检索，次数不同的就作为数据元素加入新表中，次数相同便先将系数相加，结果不为零就将结果加入新表末端，依此类推

二、顺序线性表

2.1 顺序线性表的优缺点

顺序结构的线性表的优点
- 信息储存密度高，没有浪费空间储存多余的信息来表示元素间的线性关系
- 可以随机读取表中的元素（Random Access/Arbitrary Access）
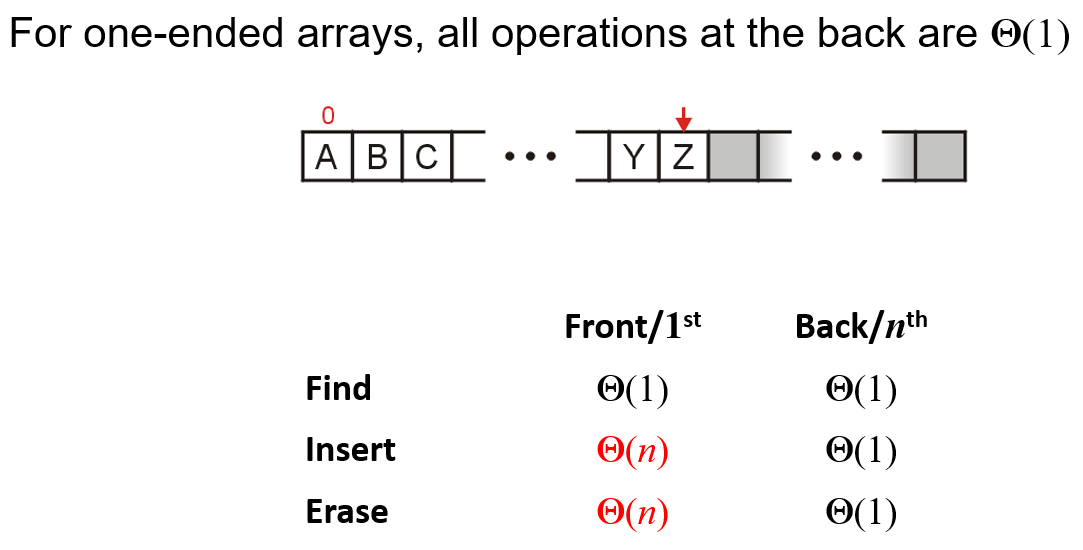
顺序结构的线性表的缺点
- 占用大块的连续内存，且需要为未来插入的元素预留额外的空间位置
- Insert和Erase函数需要移动元素来腾出位置或填补空位，导致时间复杂度较高
- 这种表是静态的存储结构，难以扩展

2.2 类结构与实现

此处使用了C++提供的数组作为内核，具体详见项目仓库

  
template <typename T>
class SequentialList
{
private:
    int capacity = 0;           //数组最大容量
    T* head = nullptr;          //数组首地址
    int length = 0;             //数组当前长度

public:
    SequentialList(int);        //构造函数
    ~SequentialList();          //析构函数

    bool IsEmpty() const;       //返回数组是否为空
    T GetElem(int) const;       //用索引读取对应元素（只读）
    int Find(const T&) const;   //返回查找对象的索引
    int GetCapacity() const;    //获取数组最大容量
    int GetLength() const;      //获取数组长度

    bool Insert(const T&, int); //插入元素到指定位置
    void PushBack(const T&);    //插入元素到数组尾部
    void Erase(int);            //删除指定位置的元素
    void PopBack();             //删除数组尾部元素
    void Clear();               //清空数组，但不销毁
};

三、链表

3.1 链表的形式与特性

链表的元素位置随机，这意味着逻辑上相邻（Adjacent）的元素节点并不在内存上相邻，每个元素节点（Node）包含以下两个部分
- Data Field：存储数据
- Pointer Field：存储其它元素的地址
链表有以下几种形式
- Linked List：每个节点只有一个指针指向后继元素
- Double Linked List：每个节点有两个指针分别指向前驱与后继
- Circular Linked List：末尾节点指向初始节点形成闭环
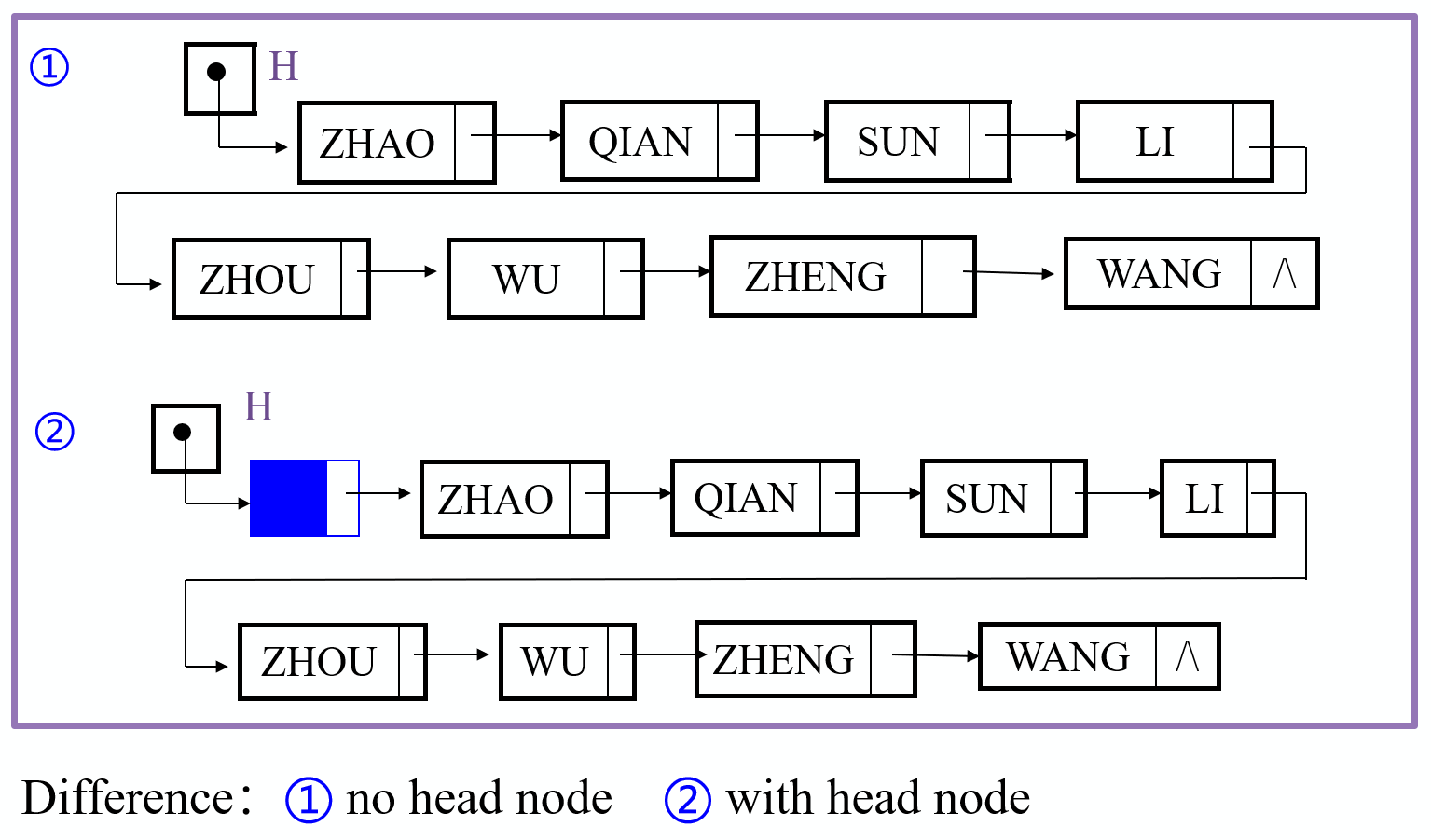
每个链表由头指针起始，指向头节点，头节点指向真正存储链表元素信息的第一个节点
- Head Pointer：指向第一个节点
- Head Node：被Head Pointer指向，存储一些关于此链表的元数据信息（Metadata）
- First Element Node：第一个存储链表信息的节点
有的链表也可以没有头节点，如下图所示，我们也可以设计一个末尾节点来存储元数据等信息，依据工程的需求可以自由发挥设计

我们每次都需要通过头指针开始，自头向尾扫描链表，直到获取到想要的元素节点，所以获取不同节点所耗费的时间是不同的
相比数组，链表存储元素没有容量大小的上限，并且其元素插入或删除不需要移动其它元素

3.2 链表类结构与实现

具体的实现参考项目仓库

  
template <typename T>
struct SingleNode
{
    T data;
    SingleNode<T>* next;
};

template <typename T>
class SingleLinkedList
{
private:
    int length = 0;                       //列表当前长度
    SingleNode<T>* head = nullptr;        //头节点指针
    SingleNode<T>* tail = nullptr;        //尾节点指针

public:
    SingleLinkedList() = default;         //构造函数
    ~SingleLinkedList();                  //析构函数

    int GetLength() const;                //获取当前链表长度
    bool IsEmpty() const;                 //查询当前列表是否为空
    T GetElem(int) const;                 //返回特定索引对应的元素值
    T* GetElemPtr(int) const;             //检索特定索引的元素的指针
    int Find(T) const;                    //返回第一个等于传入值的元素索引
    int Find(T*) const;                   //准确定位传入指针对应的元素索引
    T GetFront() const;                   //返回链表头部元素值
    T GetBack() const;                    //返回链表尾部元素值

    bool Insert(T, int);                  //插入元素到指定位置
    void PushFront(T);                    //将元素插入到链表头部
    void PushBack(T);                     //将元素插入到链表尾部
    void Erase(int);                      //删除指定位置的元素
    void PopFront();                      //删除头部元素
    void PopBack();                       //删除尾部元素
};

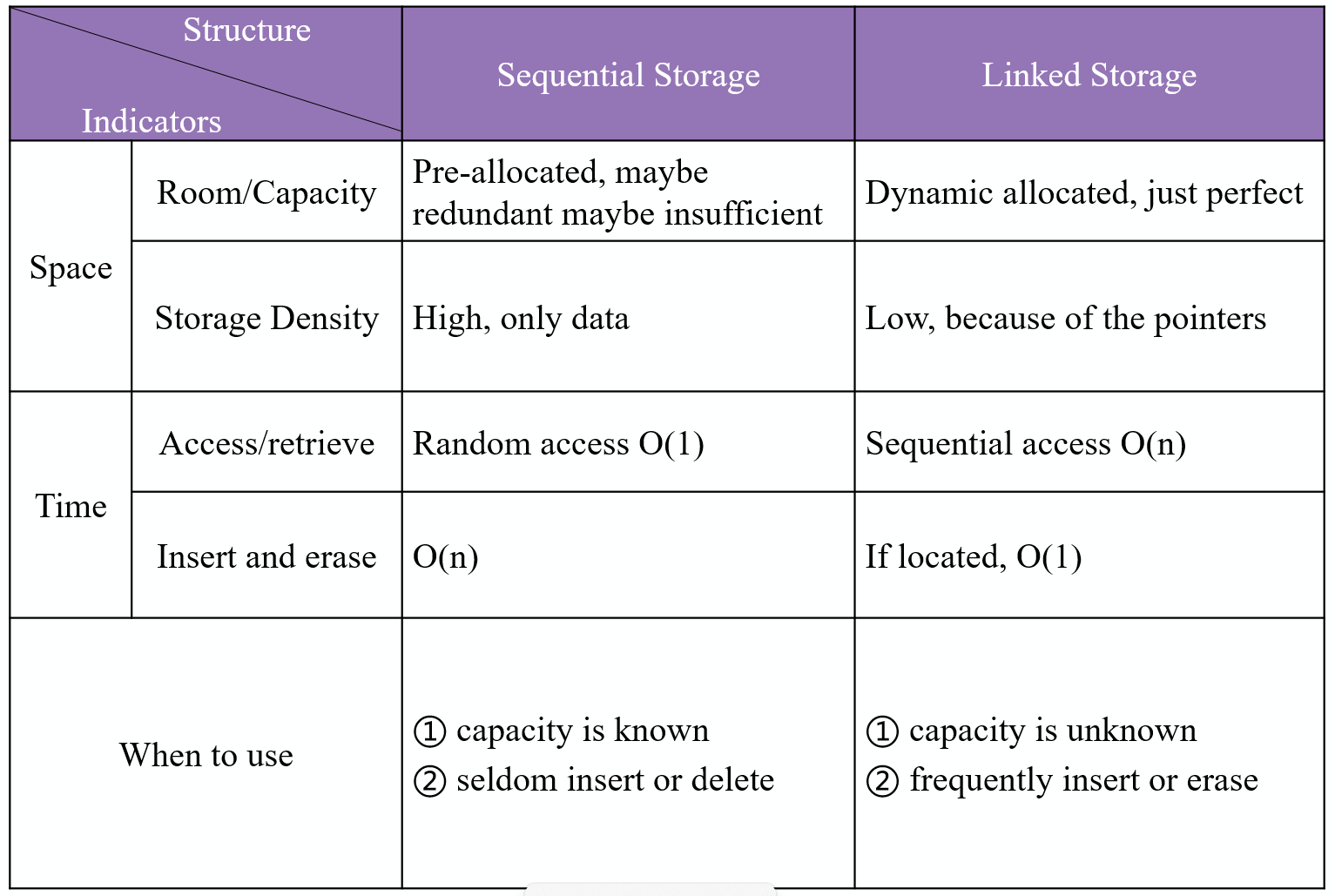
3.3 对比数组与链表

下图对比了数组和链表的空间和时间复杂度，其中链表Insert和Erase方法的$O(1)$时间复杂度指的是不考虑搜索到目标元素所耗的$O(n)$时间，他想强调的是链表增删节点无需移动其它节点

四、栈

4.1 栈的形式与应用

栈（Stack）也是一种线性表，是一种LIFO（Last-In–First-Out）结构，栈的最顶层（Top）是新加入（Push）的元素，当删除（Pop）元素的时候也是从顶层删除，无论是Push还是Pop都会更新Top的指向，如下图示意

栈可被应用于诸多方面
- 解析HTML文件格式：将各个嵌套层级的起始标签（<xxx>）依次添加到栈的顶层，遇到该层级的对应结束标签（</xxx>）后将顶层的标签Pop出栈，当遍历完整个文件后，若是栈不为空的话就说明这个文件有问题
- 判断代码格式错误：编程语言中的小括号、中括号、花括号等很类似HTML的成对标签，也可以使用栈来解析这样的脚本来检验代码的基本合法性
- 追踪函数调用进程：当某个函数调用另一个函数时意味着二者之间有先后的依赖关系，为了使得这样的链接调用不出错，栈的用处也可在此发挥
- 运算逆波兰式算式：由于乘除优先级比加减高，所以存在括号来框定计算范围，我们可以采用以下方式来进行算式计算，将每个数字添加到栈内，遇到特定符号（括号、运算符）就对先前加入到栈内的数进行特定操作

4.2 用链表实现

4.2.1 栈顶的选取

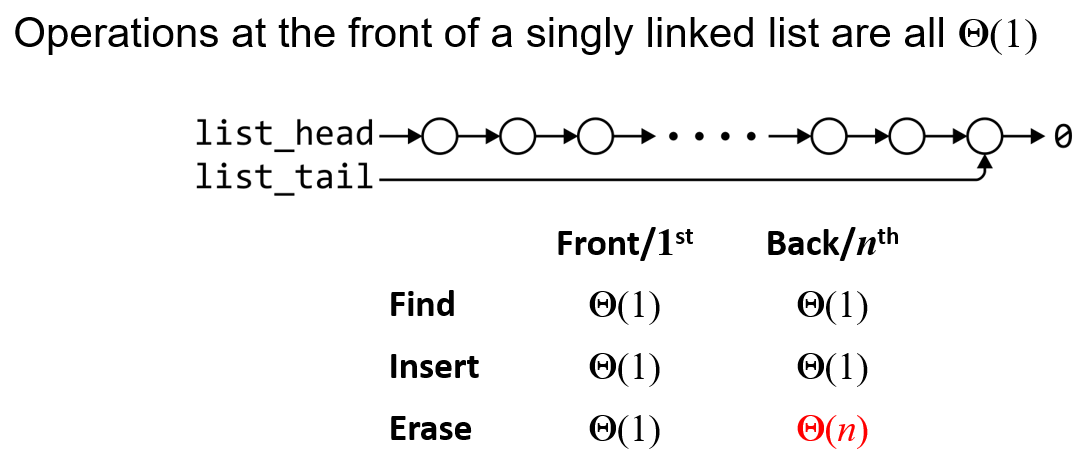
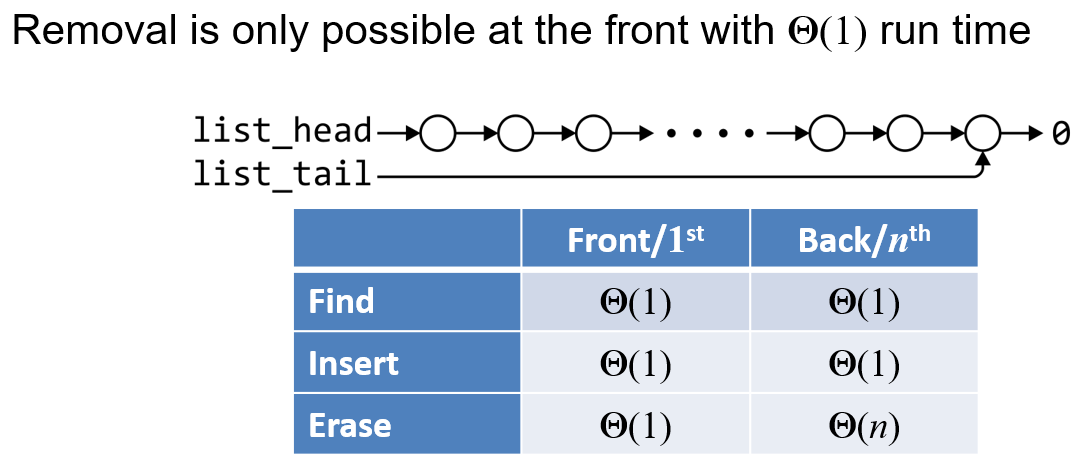
用单向链表实现栈的话，需要考虑栈顶是使用链表的头部（Head）还是尾部（Tail），参考下图所示的时间复杂度（链表为单向链表，有尾指针），其意思是
- 执行左侧对应方法，方法对象分别处于链表头部和尾部时，执行方法所耗时间复杂度
- 从图中可知只有使Insert和Erase执行的对象都在链表首位时，时间复杂度才能均为$O(1)$

至于为什么Erase操作的对象在链表尾部时，时间复杂度是$O(n)$而不是$O(1)$
- 由于此链表为单向链表，所以Erase函数无法通过尾指针访问到链表的倒数第二个元素，也就是说需要从头指针开始向后遍历，故而时间复杂度是$O(n)$
- 此时若以尾部为栈顶，每次寻找堆顶元素都要从链表的头部向尾部遍历，时间效率很低
至于为什么Insert操作的对象在链表尾部时，时间复杂度是$O(1)$而不是$O(n)$
- 因为可以让插入的新节点指向尾指针原本指向的节点，然后直接让尾指针指向新元素节点以实现插入操作
若链表不提供尾指针，那么Insert操作对于尾部元素的时间复杂度就也为$O(n)$了，此时我们就更只能选取头元素作为栈顶了

4.2.2 具体代码实现

具体的实现详见项目仓库
- 栈的Pop函数一般用于返回栈顶部的元素值并删除该元素，即“弹出”操作；但STL的pop()方法没有返回值，我在仓库中的实现同样没有返回值，而是仅让该函数执行删除操作，转而使用另一个函数GetTop来获取栈顶的值

  
//由于此栈基于写好的单向链表的栈实现（构造函数无需传入参数），所以不需写构造析构函数
template <typename T>
class LStack
{
private:
    SingleLinkedList<T> list;  //使用单向链表实现栈

public:
    bool IsEmpty() const;      //返回栈是否为空栈
    T GetTop() const;          //返回栈顶部的元素值
    
    void Push(T const&);       //将元素推送到栈的顶端
    void Pop();                //将顶端元素删除（此处不返回栈顶值）
};

4.3 用数组实现

4.3.1 实现的性能与细节

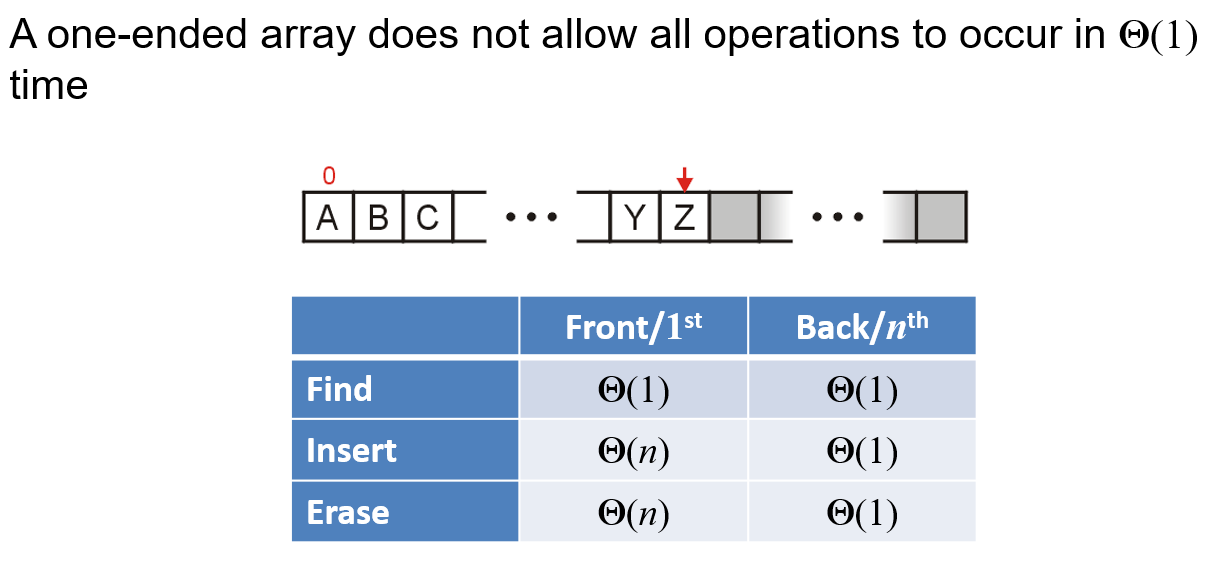
用顺序存储结构的线性表即数组来实现栈的话，从下图我们可知，应当将数组尾部当作栈顶，这样的话三个函数的操作的复杂度为$O(1)$

具体的实现详见项目仓库，由于构造函数内初始化数组的容量为某个特定的数，此后每当栈存储的数超出该容量的时候，都需进行数组内核的容量扩充，STL实现中是扩充容量为原来的两倍大

  
template <typename T>
class SStack
{
private:
    int stackSize;               //栈当前占用的大小
    int arrayCapacity;           //栈内置数组的（初始）容量
    T* array;                    //使用C++内置数组实现栈

public:
    SStack(int = 10);            //构造函数
    ~SStack();                   //析构函数

    bool IsEmpty() const;        //返回栈是否为空栈
    T GetTop() const;            //返回栈顶部的元素值
    int GetCapacity() const;     //用于测试

    void Push(T const&);         //将元素推送到栈的顶端
    void Pop();                  //删除栈的顶端元素

private:
    void DoubleTheCapacity();    //对栈的数组进行扩容 
};

4.3.2 不同扩容方式的性能

思考：关于栈的内置数组的扩容问题，为什么STL的实现将其扩容成两倍，而不是三倍四倍、抑或是加上特定大小的数呢？

在我们实现的栈中，在到达容量上限前，每次Push新元素到栈中的时间复杂度是$O(1)$，只有当在第$n$次Push且需要扩容的时候才会需要将原数组的元素转移到新数组，此时Push的复杂度是$O(n)$，我们将时间平均到每次的Push中去，就得到了

\[\text{Amortized Run Time} = O(\frac{n}{n}) = O(1)\]

上式可推广，当第n次Push的时候若触发了时间复杂度为$O(f(n))$的扩容操作（这个$f(n)$取决于扩容操作是什么），我们就可以算出平均的占用时间来评估扩容操作的性能

\[\text{Amortized Run Time} = O(\frac{f(n)}{n})\]

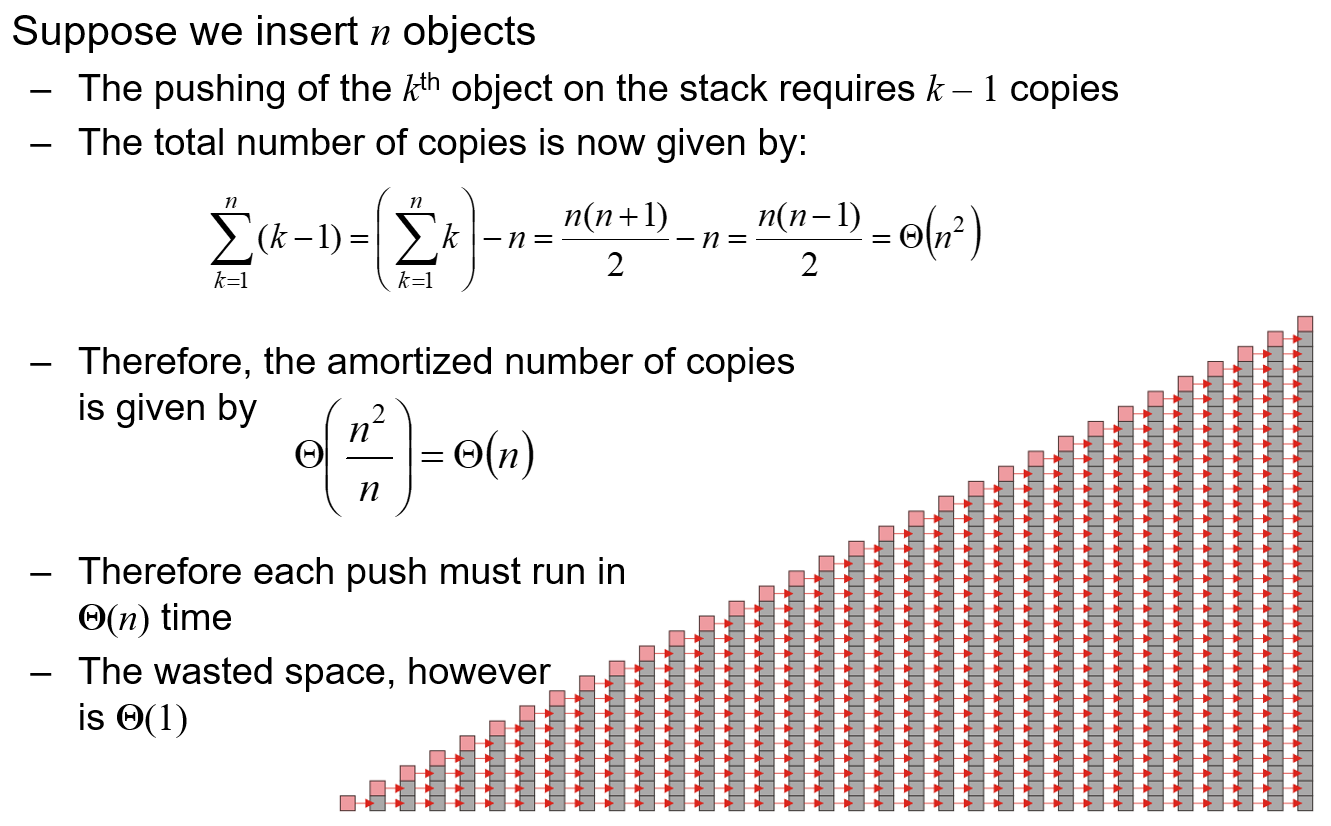
假设我们的扩容操作是每次为容量+1，这意味着每次添加新元素都需要扩容，参考下图分析，此时的单次操作的平均时间复杂度就为$O(n)$，优点就是浪费的空间很少

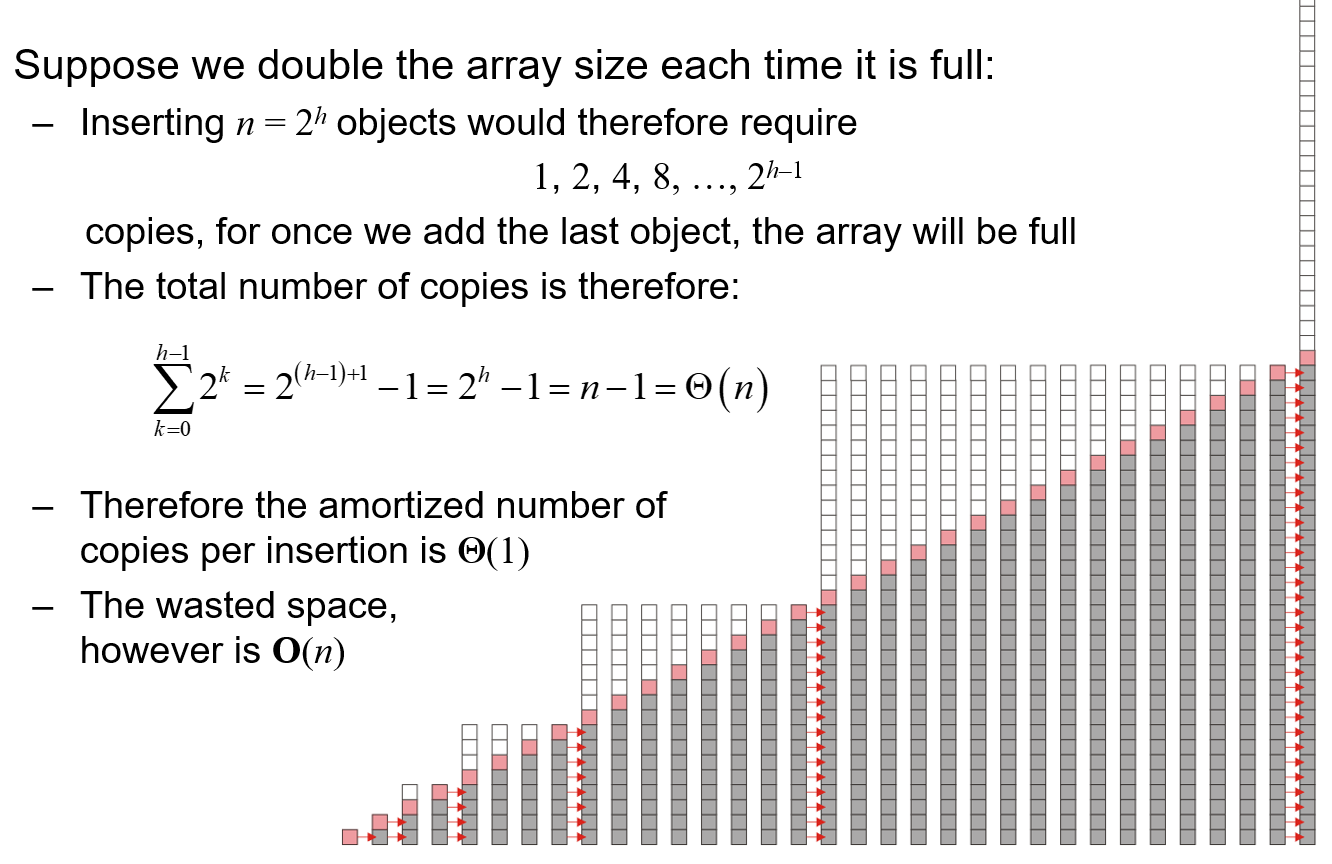
若扩容操作是容量x2，此时每此执行第$n=2^m,m \in N$次Push时就会发生扩容操作，如下图计算可得平均时间复杂度为$O(1)$，但是空间浪费就比+1的大

对于每次扩容+m或乘上r倍的方式的性能（时间与空间复杂度）如下表所示

五、队列

5.1 队列的形式与应用

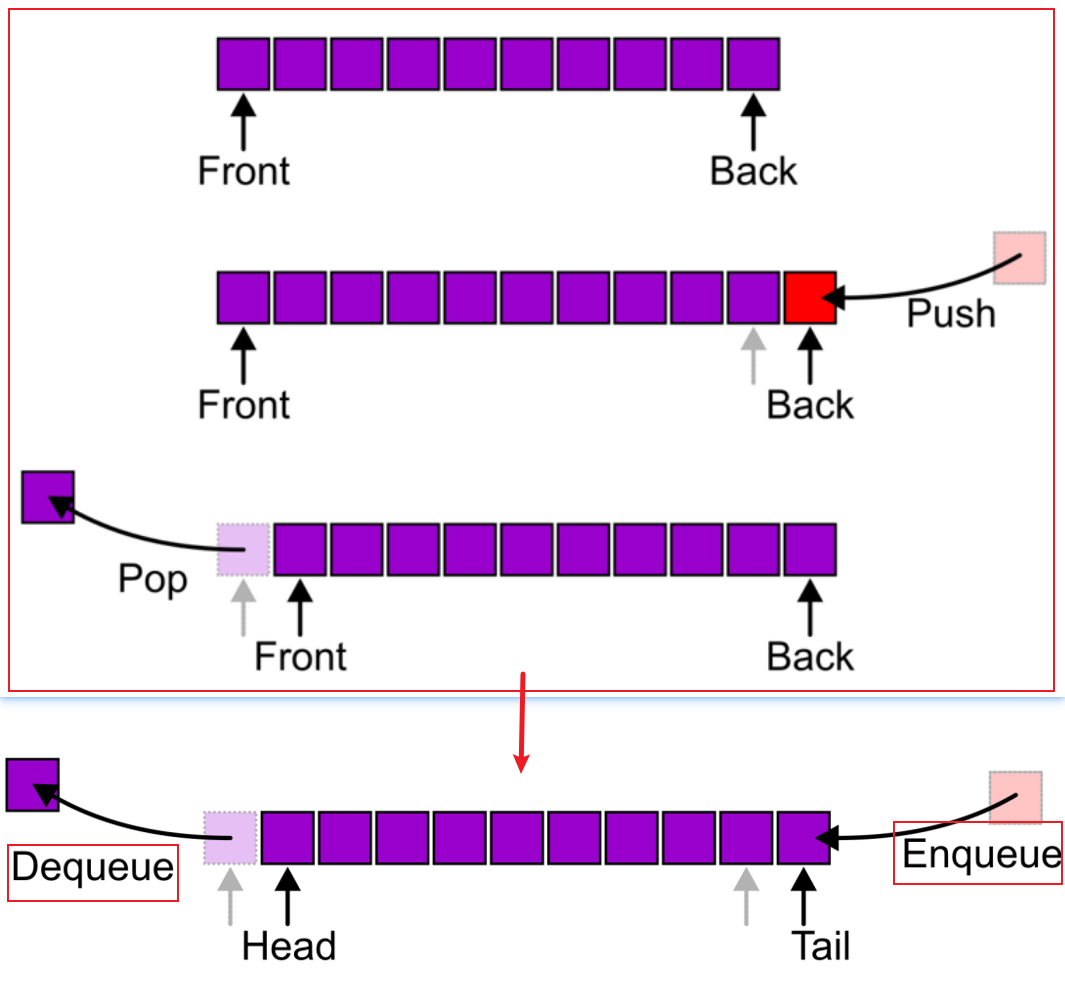
队列（Queue）是一种FIFO（First-In–First-Out）的线性表，像排队一样，先入队（Enqueue）的元素会被先取出（Dequeue），这意味着Pop操作会优先删除队列头部的元素，如下图所示

队列常应用在客户端服务端（Client-Server）模型上，比如用于处理多个用户向一个或多个服务端请求服务，具体点比如网购/售票平台、网页、数据库等，广度优先算法也使用到了队列

5.2 用链表实现

使用链表实现队列的话，要考虑每次将新元素添加到链表的头部还是尾部，如下图所示
- Erase函数仅在作用对象为链表头部元素时时间复杂度才是最低的$O(1)$
- 故应将链表头部当作队列头，即每次入队都需将新元素Insert到链表尾部

具体的实现详见项目仓库

  
template <typename T>
class LQueue
{
private:
    SingleLinkedList<T> list;  //单向链表内核

public:
    bool IsEmpty() const;      //判断是否为空
    T GetFront() const;        //获取下一个将被取出队列的元素

    void Push(T const&);       //将新加入的元素放入链表尾部
    void Pop();                //将链表头部的元素删除
};

5.3 用数组实现

对于普通的数组，每次在头部插入或者删除元素的时间复杂度都很高（因为插入新元素要向后挤，删除元素需要后面的元素向前补位）

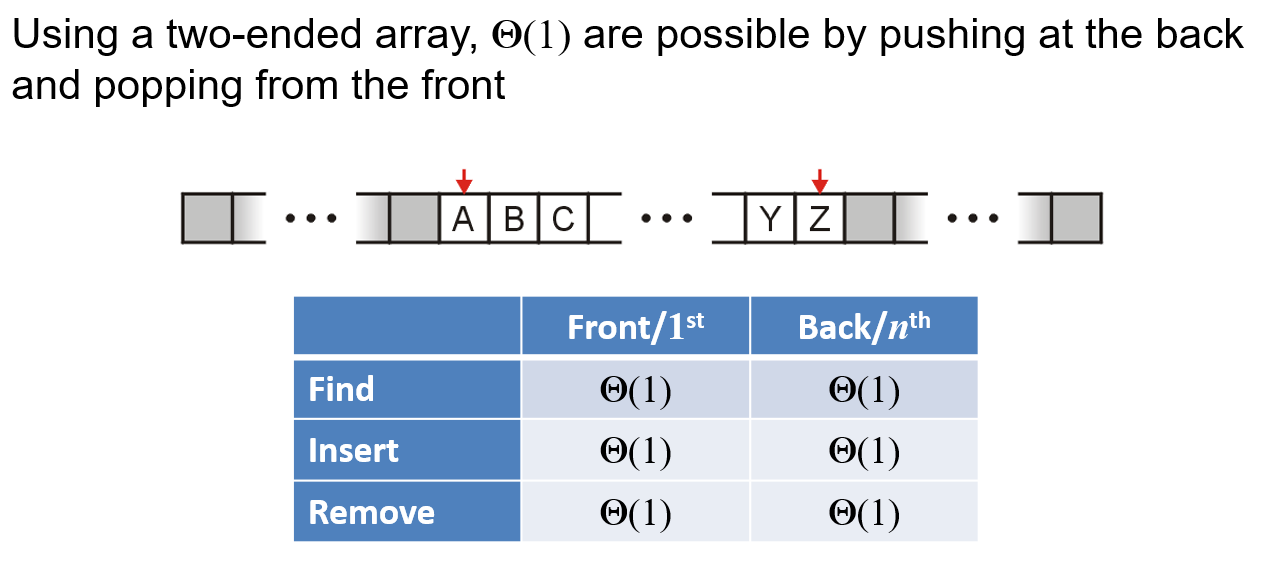
对于循环数组（Circular Array），在头尾两端插入或删除的复杂度都为$O(1)$，避免了上述问题，这个所谓循环数组其实还是基于普通数组，对于实现队列这种FIFO类型的结构十分合适

循环数组的实现示意如下

具体的实现详见项目仓库

  
//使用循环数组作为内核，使得首尾两端插入或删除元素的时间复杂度均为O(1)
template <typename T>
class SQueue
{
private:
    T* array;                   //数组首地址
    int queueSize;              //队列当前存了多少对象
    int arrayCapacity;          //内核数组的（初始）容量
    int frontIdx;               //循环数组的头部元素（队列前端）索引
    int backIdx;                //循环数组的尾部元素（队列后端）索引

public:
    SQueue(int = 10);           //构造函数
    ~SQueue();                  //析构函数

    bool IsEmpty() const;       //空判断
    T GetFront() const;         //获得队列前端元素

    void Push(T const&);        //将新元素推送到数组尾部
    void Pop();                 //将数组头部即队列前端的元素删除

private:
    const DoubleTheCapacity();  //内核数组扩容
};

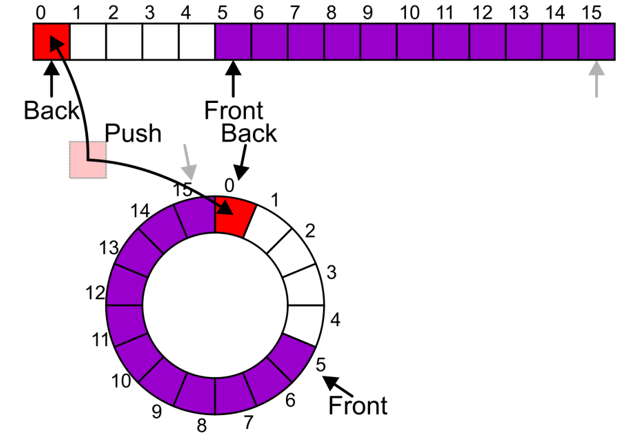
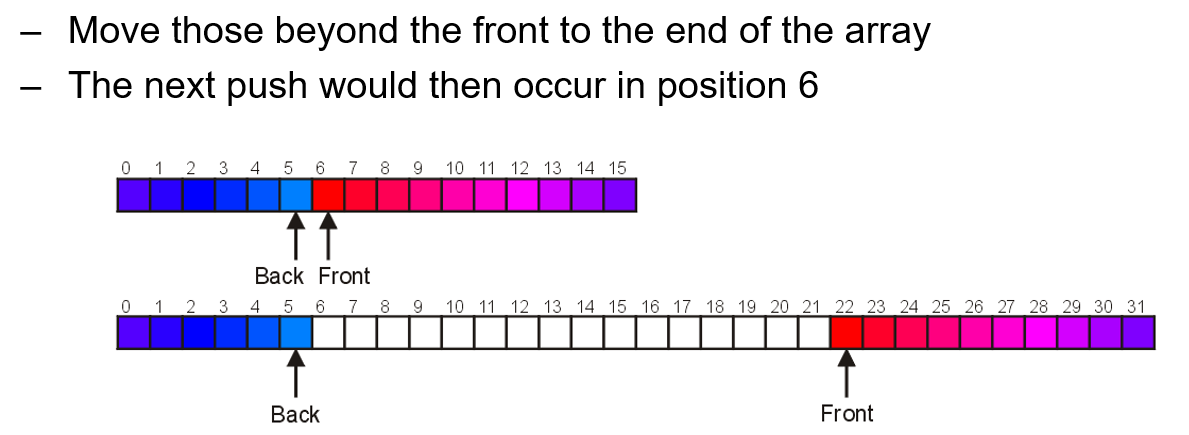
其中Push和Pop两个函数十分重要，我们不能在backIdx移动到了(arrayCapacity - 1)后就直接扩容，因为这期间可能会Pop弹出队列前端元素，会导致队列有空位，这时候直接扩容就会导致空间浪费，我们应当如下图所示，将新元素Push到空位上，直到真正的所有空间都被占满后才进行扩容

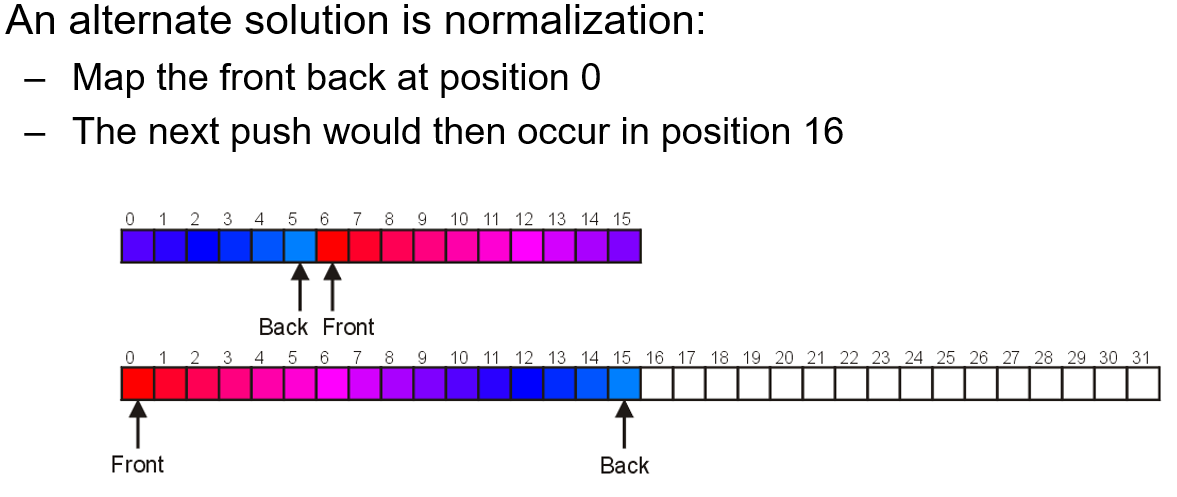
扩容之后不能直接将旧数组的元素复制到新数组，那样会顺序错乱，有两种如下图的解决方法

六、双端队列

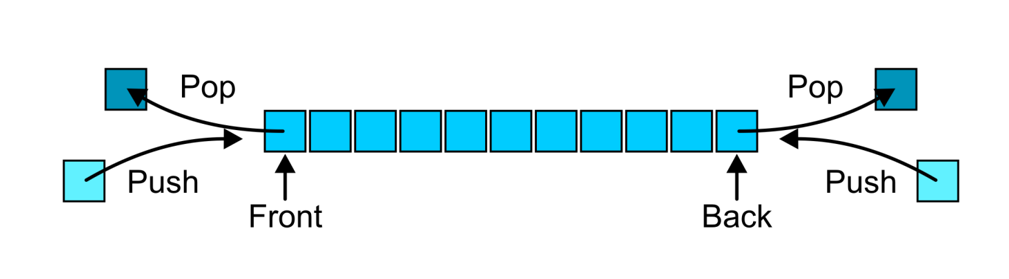
6.1 双端队列的形式与应用

双端队列（Double Ended Queue）允许头尾两端的插入和删除，这意味着这玩意儿除了特殊需求的应用，还可以被当作普通的栈或队列使用

6.2 实现双端队列

若要用链表实现，最好使用双向链表，因为在实现队列的时候我们看到了，有头尾指针但是只能从头指向尾的单向列表，由于无法从尾指针搜寻到尾指针前一项元素，故而导致必须从头指针向尾部遍历，导致想要删除尾端的元素的时间复杂度是$O(n)$；双端队列因为要两端都能插入或删除，所以无法规避这个$O(n)$，故而要使用双向链表
用数组实现的话同样可以使用循环的数组，其实现比队列的实现略有不同，区别就是双端队列的frontIdx和backIdx都有了递减的可能（队列的二者只需要递增即可，递增过程中触底了就直接返回0，然后继续递增），但只要内核数组存满了就扩容两倍就行了

学科笔记, 数据结构

数据结构 C++

本文由作者按照 CC BY-NC-SA 4.0 进行授权