常见树结构分析及其实现

该博客包含关于一般树、一般二叉树、二叉搜索树等基本结构的相关分析，以及部分结构的无STL的C++实现

发表于 2024/09/27 更新于 2025/01/06

作者 WhythZ

45 分钟阅读

常见树结构分析及其实现

具体代码的实现参考我的项目仓库

一、关于树

1.1 树的定义

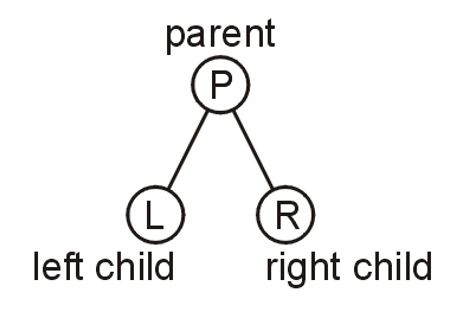
每个树有一个根节点（Root Node），从这个节点向下延伸出其它节点
除了根节点外（根节点没有前驱）的每个节点只能有唯一一个前驱节点
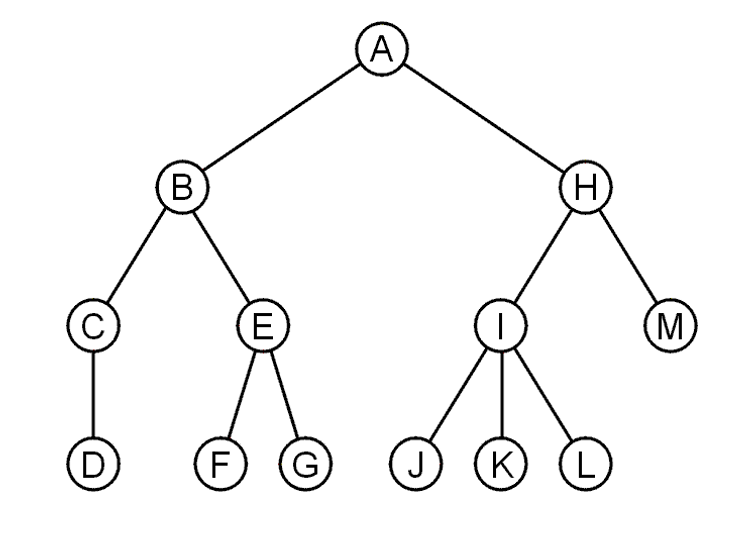
每个节点有零个或一个或多个后继节点，节点拥有的子节点个数称为这个节点的度（Degree），如下图中$Deg(I)=3,Deg(E)=2$

度为$0$的节点又称为叶节点（Leaf Node），此外的所有点都叫做内部节点（Internal Node）

1.2 树的分类

1.2.1 按分支数量限制分类

按照每个树节点的度上限（能延伸出的最大叉数），一般将树分为二叉树和多叉树，此处分类不一定完全，仅供参考
- 多叉树
  - 多路搜索树
  - B树
  - B+树
- 二叉树
  - 普通二叉树
    - 完满二叉树
    - 完全二叉树
    - 完美二叉树
  - 普通的二叉搜索树
  - 平衡的二叉搜索树
    - AVL树
    - 红黑树
    - BB($\alpha$)树

1.2.2 按节点的有序性分类

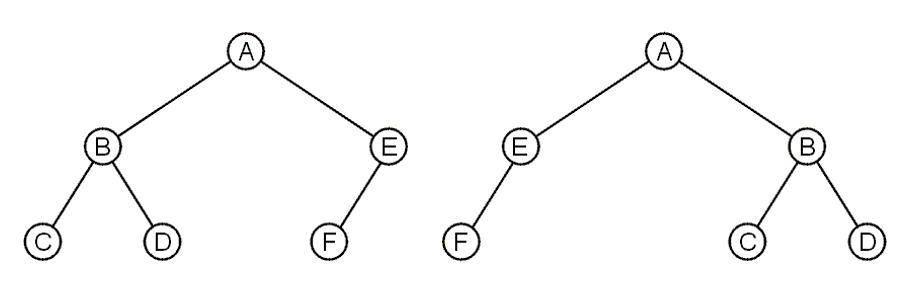
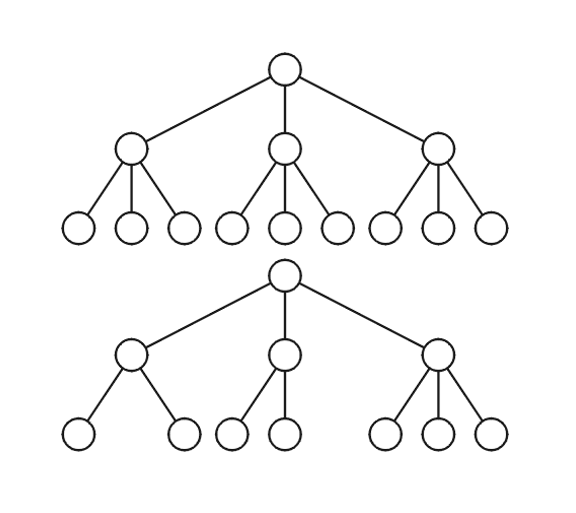
下图的这两个树在不考虑顺序的情况下视为相等；如果考虑顺序的话，如节点上的字母所示，那么二者就是不相同的

将树按照有序性分类，可分为无序树（其节点的键值无特定大小关系）与搜索树/查找树（其基本特征是任意一个节点所包含的键值，大于等于左孩子的键值，小于等于右孩子的键值）

1.3 路径、节点深度、树高度

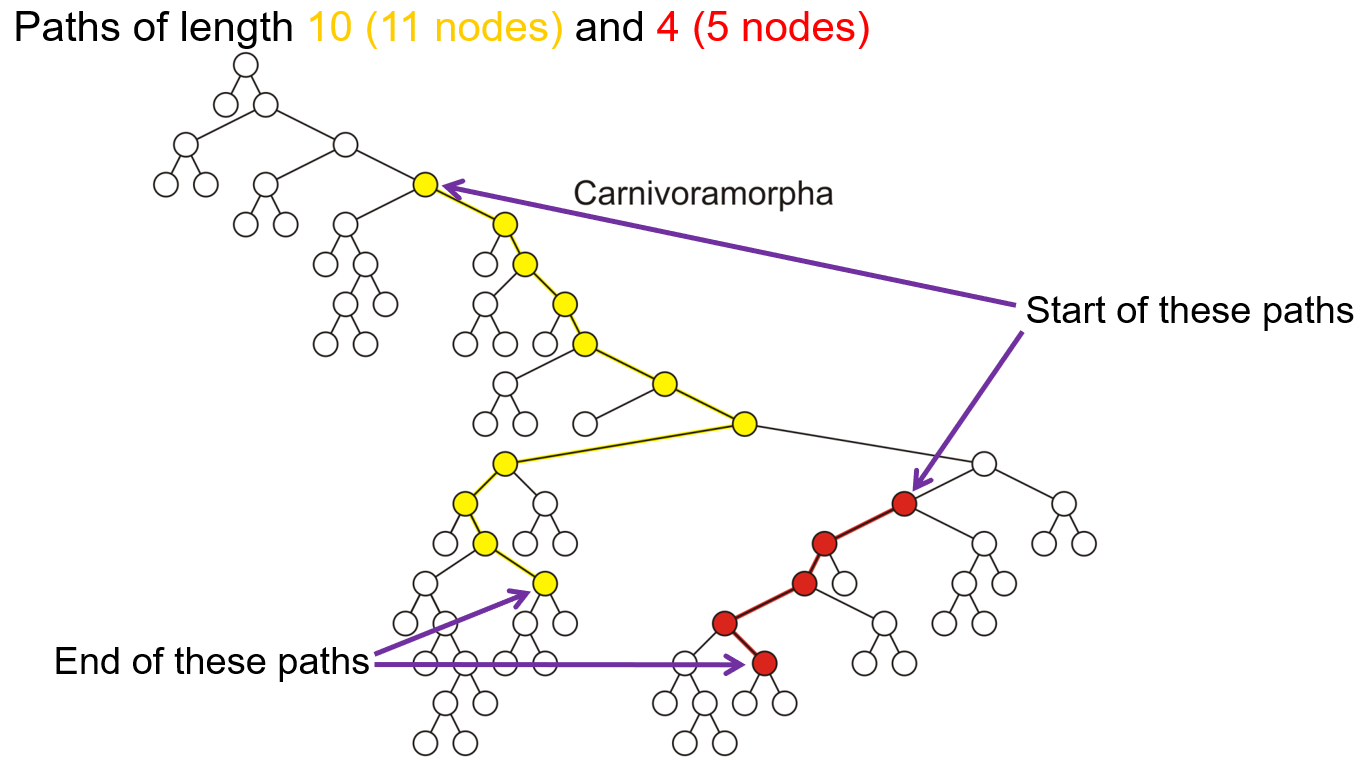
为了找到树的某个节点，我们从该节点上游的某个节点出发，能找到唯一一条路径（Path）抵达该目标节点
路径是节点的集合，路径的长度（Length）不计初始节点，如下图所示

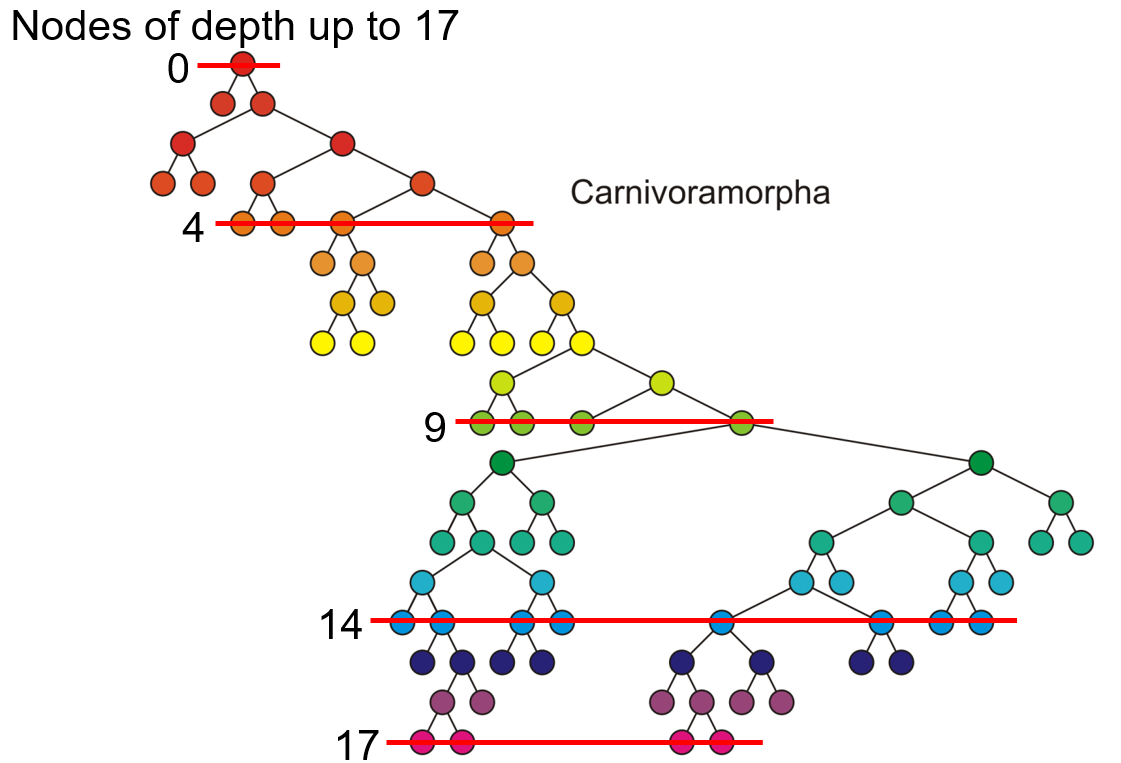
对某个节点，从根节点触发，一定能找到一条唯一的路径抵达该节点，此路径的长度称为该目标节点的深度（Depth）

所有节点中的最大的深度称为树的高度（Height），一个只有根节点的树的高度为$0$，空的树的高度被定义为-1

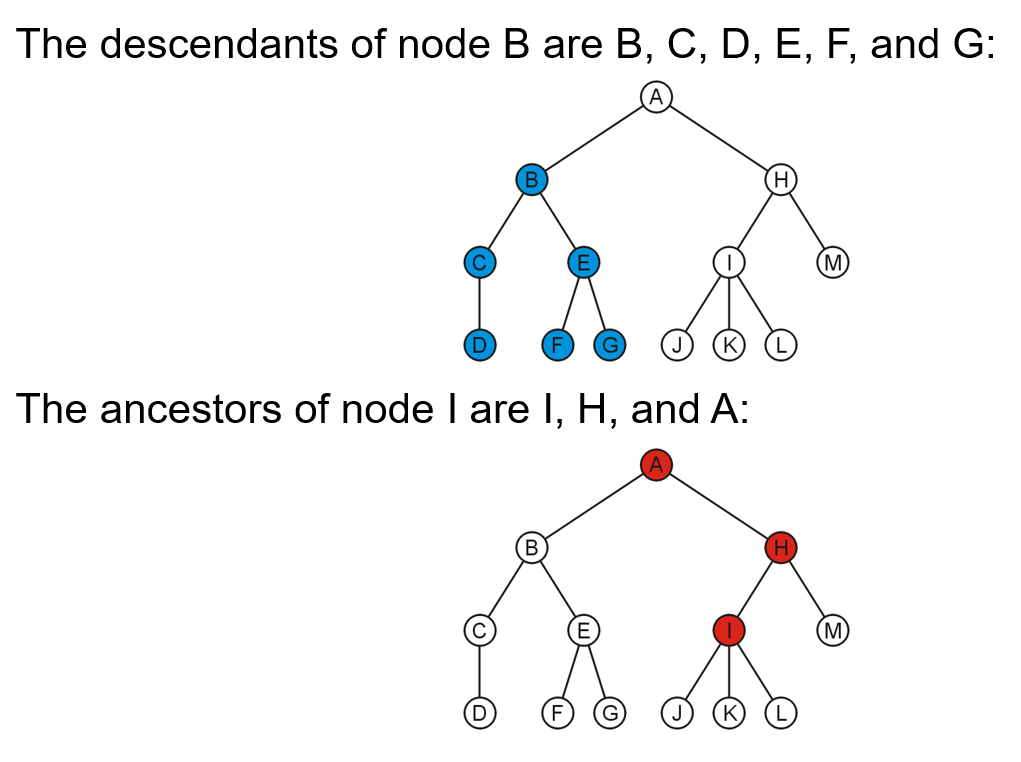
1.4 祖先与后代

如果存在一条从节点A到B的路径，那么A称为B的祖先节点（Ancestor），B称为A的后代节点（Descendant），所以根节点是所有节点的祖先
通过定义可知A同时是自己的祖先与后代，如果A是B的祖先且A与B不是同一个节点，那么B是A的严格后代（Strict Descendant）
一个节点及其所有后代实际上就是这个树的一个子树（Subtree）

1.5 树的应用

各类软件的文件资源管理器中的文件就是按照树的层次结构存储的
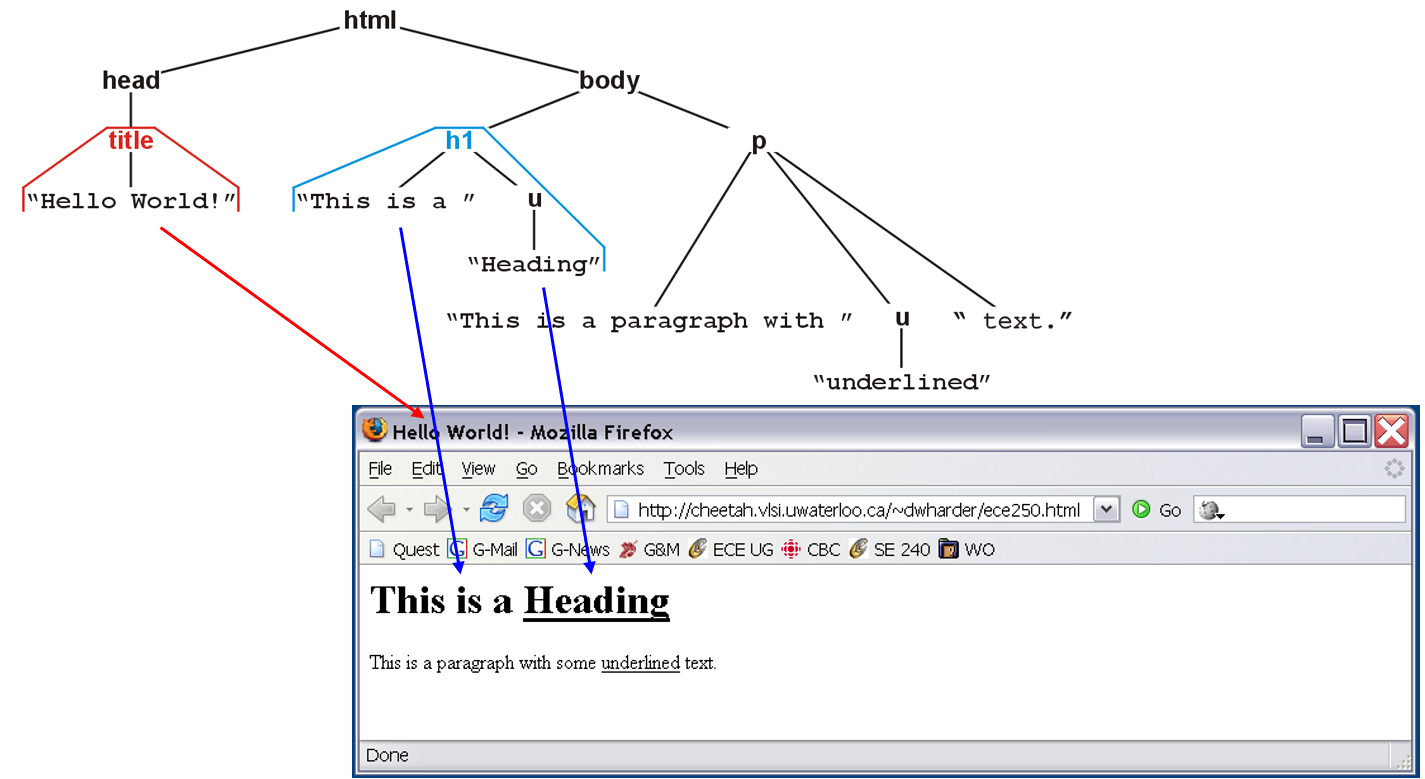
HTML的结构就是树状结构，参考下列HTML文件及其图示

  
<html>
	<head>
		<title>Hello World!</title>
	</head>
	<body>
		<h1>This is a <u>Heading</u></h1>

		<p>This is a paragraph with some
		<u>underlined</u> text.</p>
	</body>
</html>

二、一般树

2.1 代码实现

为了实现各种类别的树，我们得先从底层的基本结构“节点”开始实现，下面这个类指的是一个树节点，其拥有一个父节点指针和一组子节点（用链表存储，链表的实现采用了我自己写的单向链表实现），具体实现详见项目仓库

  
//最基本的树节点结构，存储其父子两层节点的指针，以及存储在该节点数据
template <typename T>
class TreeNode
{
protected:
    T nodeData;                                  //该节点存储的数据
    TreeNode<T>* parentNode;                     //该节点的父节点指针
    SingleLinkedList<TreeNode<T>> childList;     //该节点的子节点

public:
    TreeNode(const T& = T());                    //构造函数，初始化节点存储的数据
    TreeNode<T>& operator=(const TreeNode<T>&);  //运算符=的重载，实现深拷贝
    TreeNode(const TreeNode<T>&);                //拷贝构造，实现深拷贝

    T GetNodeData() const;                       //获取该树节点存储的数据值
    bool IsRoot() const;                         //该节点是否是根节点（树的发端）
    bool IsLeaf() const;                         //该节点是否是叶节点（树的末端）
    int GetSize() const;                         //获取以该节点及其所有后代的个数
    int GetDepth() const;                        //获取以该节点为根节点的树的深度
    int GetDegree() const;                       //获取该节点的度，即子节点个数
    TreeNode<T>* GetParentPtr() const;           //获取指向父节点的指针
    TreeNode<T>* GetChildPtr(int) const;         //以索引获取指向某子节点的指针
    int FindChildIdx(TreeNode<T>*) const;        //搜索子节点在链表中的索引
    void PrintNeighbor() const;                  //打印该节点自身及其相邻两层，共三层
    void PrintTree() const;                      //完整打印以该节点为根节点的树

    void AddChild(TreeNode<T>*);                 //以传入节点的方式添加子节点
    void AddChild(T);                            //以传入新元素的方式添加子节点
    void DelChild(int);                          //通过索引删除子节点
    void DelChild(TreeNode<T>*);                 //通过地址删除子节点

protected:
    void PrintTree(int) const;                   //依据传入深度打印出基于相应层级的树
};

该树节点的析构会调用内置链表的析构函数，对各级后代节点进行逐层析构
同时注意要对赋值运算符进行重载，使其能够进行深拷贝，这个运算符在链表添加新的树节点对象的时候就会被调用，所以重载函数的实现内不能使用此处的AddChild等函数（这些函数都依赖于重载的=运算符），否则会造成循环依赖
而拷贝构造的实现则可以依赖于AddChild函数（其实现原理为把传入节点深拷贝到堆区，再将其附加到父节点上）或是赋值运算符

2.2 BFS与DFS遍历

2.2.1 广度优先遍历

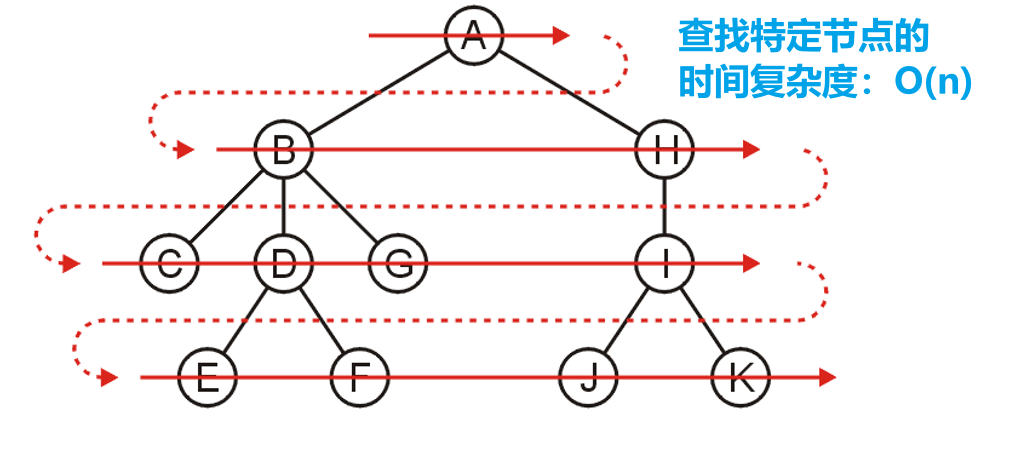
广度优先遍历（Breadth-First Traversal）即广度优先搜索（BFS），其查找树的特定节点的方法就是依次遍历完每一层深度的所有节点，直到找到目标节点

其实现基于队列（Queue），首先先将根节点添加到队列中，然后将其所有子节点依次添加到队列尾部，直到根节点的所有子节点都入队了后，就开始从队列头部的子节点开始依次出队，每出队一个节点就将其子节点依次添加到队尾，直到该节点的所有子节点入队，依此类推
简单来说，就是将某节点的子节点全部入队后，才会开始对队列进行Pop操作，每次Pop取出一个节点元素就对其字节点进行入队操作，重复此循环即可；同时若想达成搜索的目的，在每个节点入队时检查其是否为目标节点即可
这样查找特定树节点所耗费的时间复杂度为$O(n)$，而空间复杂度则视每层深度的节点数而定，空间占用一般较大，即内存耗费大

2.2.2 深度优先遍历

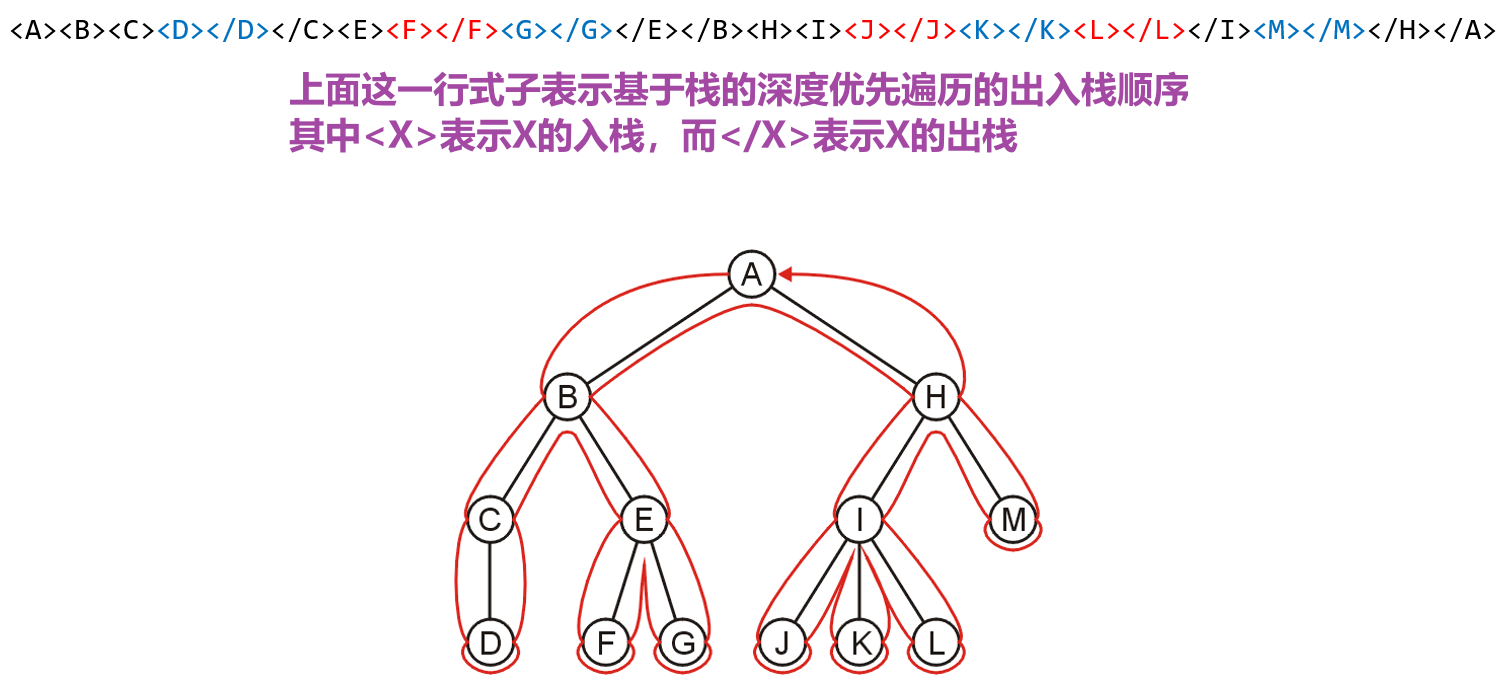
深度优先遍历（Depth-First Traversal）即深度优先搜索（DFS），其对树的遍历方法即探索单个分支直到底部（直到入队的节点为叶节点），然后折返回最近的一个分岔路口，选取路口的下一个分支进行探索直到触底，依此类推直到找到目标节点

其实现基于栈（Stack），我们以上图即先将根节点入栈，检测到根节点有子节点就将第一个子节点入栈，继续此操作直到最后入栈的节点为叶节点，将叶节点出栈，返回上一个节点，其若有另一个分支（若无分支则直接将此节点出栈），则将另一个分支的节点入栈，然后重复上述操作；最终直到返回根节点时即为探索完了此分支，则可以继续开始探索根节点的下一个分支，最终直到探索完了会回到根节点，根节点第一个入栈，最后一个出栈
这样查找特定树节点所耗费的时间复杂度同样为$O(n)$，至于对于二叉树来说，空间复杂度就等于$O(h)$，其中$h$即为该树的深度

2.2.3 迭代器代码实现

下面是一个专门用于遍历树的迭代器类，其可适配多种树结构（以对应树节点指针模板化该类以得到对应的迭代器对象），只需要对应树种提供需求的接口函数即可套用，具体的BFS与DFS的算法实现参考项目仓库

  
//X指的是树节点指针，比如TreeNode<T>*，或BinaryTreeNode<T>*
template <typename X>
class TreeIterator
{
private:
    X root;                         //被遍历的树对象的根节点
    SQueue<X> queue;                //队列，存储以BFS遍历的树节点指针结果
    SStack<X> stack;                //栈，存储以DFS遍历的树节点指针结果

public:
    TreeIterator(X);                //构造函数初始化被遍历的对象
    void TraversalBFS();            //以BFS遍历打印树的所有节点
    void TraversalDFS();            //以DFS遍历打印树的所有节点

private:
    void TraversalBFS(X);           //以BFS遍历打印传入节点的所有后代节点
    void TraversalDFS(X, int = 0);  //以DFS遍历打印传入节点的所有后代节点
};

三、二叉树

3.1 二叉树的基本概念

3.1.1 左右子树

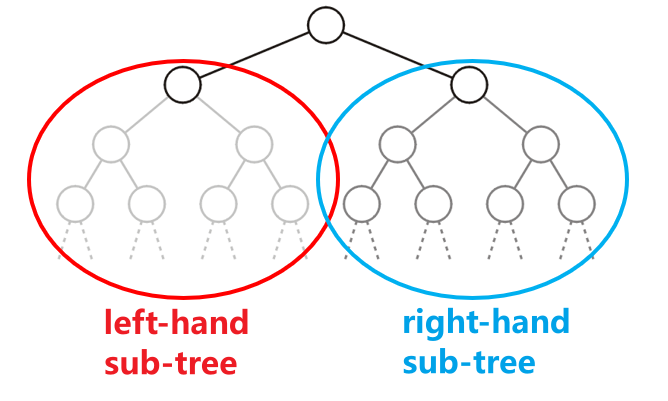
二叉树（Binary Tree）对其每个节点有要求，即任意节点最多有$2$个子节点，或者说最多拥有$2$个子树（Sub-Tree）

每个节点的子树的顺序不可颠倒，分为左子树与右子树，即便只有一个子树，这个子树也拥有左右的顺序，应当按照这个顺序进行摆放，如下图中的样本所示

3.1.2 满节点与空节点

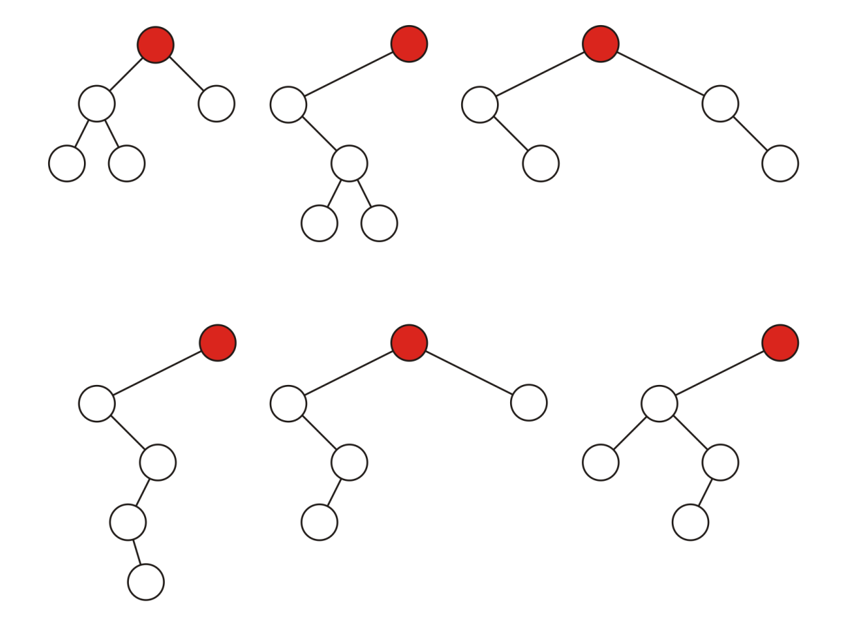
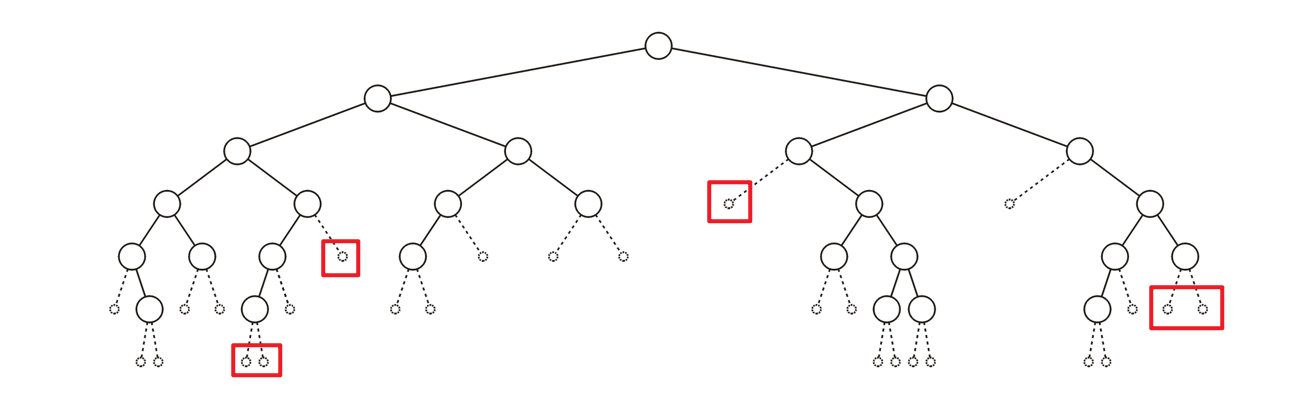
如果一个二叉树节点的左右子树都是非空的（如果只有左子树，那么就说明右子树为空，否则就是非空，即便只有一个叶节点），那么这个节点就是满节点

而那些空子树（Null Sub-Tree）位置，或称空节点（Empty Node）位置，其上都是可以附加上新的枝干的，如下图红框所示

3.1.3 满二叉树

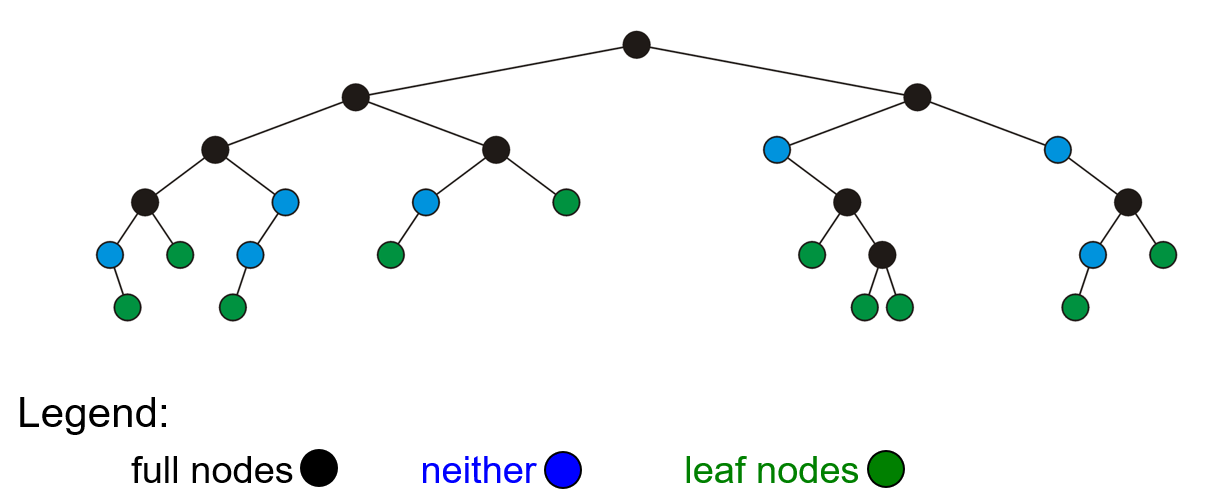
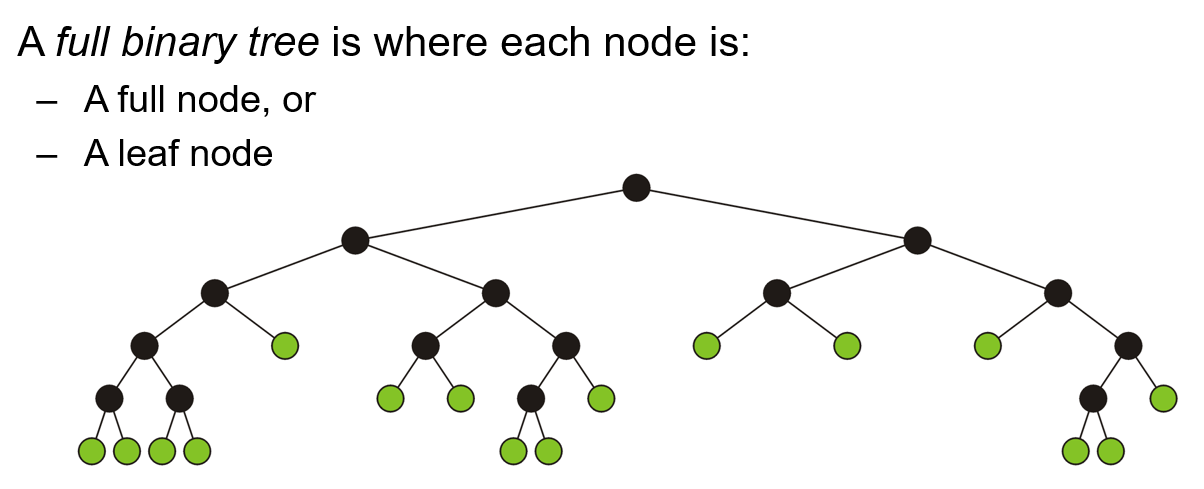
满二叉树（Full Binary Tree）即所有节点要么是满节点，要么是叶节点的二叉树，除此之外的二叉树都是非满二叉树

3.2 代码实现

我之前已经实现了一个较为完善的树节点类，二叉树节点与这种树节点是Is-A的关系，所以可以通过继承关系来实现二叉树，同时要注意以下几点
- 以protected权限进行继承，杜绝基类的公共方法通过子类对外开发，因为基类的许多方法使用了其自身以及衍生的数据类型（如TreeNode<T>或TreeNode<T>*）作为返回值或参数列表，在子类（BinaryTreeNode<T>）中我们无法通过重写虚函数来改变返回值类型或参数列表数据类型，所以只能将这些方法变为protected，再通过重载这些方法来提供对外接口（基类公开的所有方法都必须在子类中有对应的重载，否则就违背了里氏替换原则）
- 左右子节点不能仅用childList的0与1索引位置元素分别表示，因为存在着一个二叉树节点只有右子节点而无左子节点的情况，此时索引1是非法的，针对这种情况就需要多在二叉树节点类中多维护一对诸如leftSubNode与rightSubNode的指针（如一个二叉树节点仅有右子节点时，rightSubNode指针就指向childList的0索引位置，leftSubNode则指向nullptr，此时若新增一个左子节点，leftSubNode就会指向1索引位置）
继承的重写太过麻烦，不建议这样实现，我们可以在二叉树类内维护一个内核TreeNode<T>作为成员变量，对其子节点数进行限制即可，这种方法可以使得二叉树节点类拥有TreeNode<T>的所有接口，这样就可以套用后者的迭代器到前者
我们也可以直接重新写一个二叉树节点类，这样可以降低脚本间的耦合度，但是这样的话，二叉树节点类就无法共享TreeNode<T>的函数接口（若前者想使用后者的迭代器类，就需要提供同名接口），我在项目仓库中是重新写了一个

  
//二叉树节点类
template <typename T>
class BinaryTreeNode
{
protected:
    T nodeData;                                  //该节点存储的数据
    BinaryTreeNode<T>* parentNode;               //该节点的父节点指针
    BinaryTreeNode<T>* leftChild;                //该节点的左子节点（树）指针
    BinaryTreeNode<T>* rightChild;               //该节点的右子节点（树）指针

public:
    //构造函数，初始化节点存储的数据
    BinaryTreeNode(const T & = T());
    //析构函数，此类没有子节点链表帮我们析构
    ~BinaryTreeNode();
    //运算符=的重载，实现深拷贝
    BinaryTreeNode<T>& operator=(const BinaryTreeNode<T>&);
    //拷贝构造，实现深拷贝
    BinaryTreeNode(const BinaryTreeNode<T>&);

    T GetNodeData() const;                       //获取该树节点存储的数据值
    bool IsRoot() const;                         //该节点是否是根节点（树的发端）
    bool HasLeftChild() const;                   //该节点是否有左子节点
    bool HasRightChild() const;                  //该节点是否有右子节点
    bool IsLeaf() const;                         //该节点是否是叶节点（树的末端）
    int GetSize() const;                         //获取以该节点及其所有后代的个数
    int GetDepth() const;                        //获取以该节点为根节点的树的深度
    int GetDegree() const;                       //获取该节点的度，即子节点个数
    BinaryTreeNode<T>* GetParentPtr() const;     //获取指向父节点的指针
    BinaryTreeNode<T>* GetLeftChildPtr() const;  //获取指向左子节点（树）的指针
    BinaryTreeNode<T>* GetRightChildPtr() const; //获取指向右子节点（树）的指针
    void PrintTree() const;                      //完整打印以该节点为根节点的树

    void SetLeftChild(BinaryTreeNode<T>*);       //以传指针的方式设置左子节点（会覆盖）
    void SetLeftChild(T);                        //以传值的方式设置左子节点（会覆盖）
    void SetRightChild(BinaryTreeNode<T>*);      //以传指针的方式设置右子节点（会覆盖）
    void SetRightChild(T);                       //以传值的方式设置右子节点（会覆盖）
    void DelLeftChild();                         //删除左子节点
    void DelRightChild();                        //删除右子节点

protected:
    void PrintTree(int, int) const;              //打印对应深度和类型的树
};

3.3 二叉树的遍历

前文提到的BFS与DFS可以套用在任意树种上，包括二叉树，而此处提到的三种遍历方法都是只适用于二叉树结构的

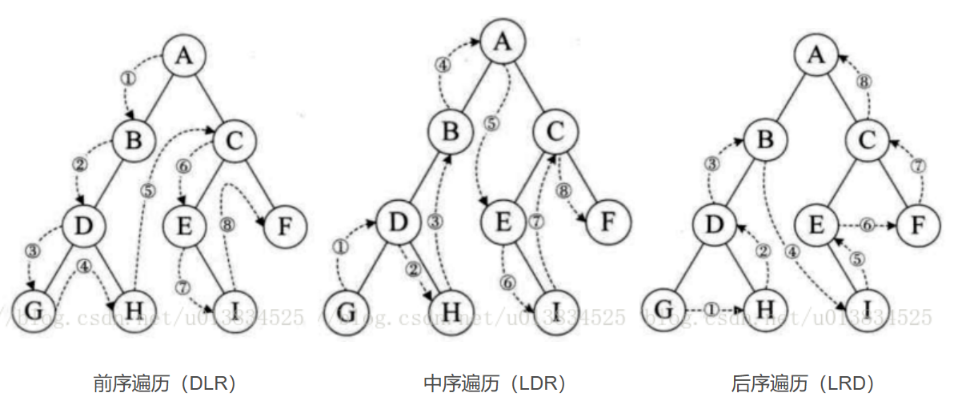
3.3.1 前序遍历（Preorder）

对于下面这个二叉树，三个方法将会利用此树进行测试（传入根部的111节点指针）

  
//-[111]
//        -L[222]
//                -L[444]
//                        -L[888]
//                        -R[ ]
//                -R[555]
//        -R[333]
//                -L[666]
//                        -L[999]
//                        -R[ ]
//                -R[777]

下图的2代表的是父节点，Pre指的是2在1和3之前打印（我们注意到三种打印方法具有一个共同点，就是右子节点永远在左子节点后打印，所以唯一在变的就是父节点什么时候打印）

  
template <typename X>
void BinaryTreeIterator<X>::TraversalPreOrder(X _node)
{
    //防止无限循环
    if (_node == nullptr)
        return;
    //打印顺序：自己--左子--右子
    std::cout << "<" << _node->GetNodeData() << ">";
    TraversalPreOrder(_node->GetLeftChildPtr());
    TraversalPreOrder(_node->GetRightChildPtr());
}

我们使用此遍历方法得到的结果如下，这个结果与深度优先遍历得到的结果是一致的

//<111><222><444><888><555><333><666><999><777>

3.3.2 中序遍历（Inorder）

顺序是2在13中间（In）被打印

  
template <typename X>
void BinaryTreeIterator<X>::TraversalInOrder(X _node)
{
    //防止无限循环
    if (_node == nullptr)
        return;
    //打印顺序：左子--自己--右子
    TraversalInOrder(_node->GetLeftChildPtr());
    std::cout << "<" << _node->GetNodeData() << ">";
    TraversalInOrder(_node->GetRightChildPtr());
}

对于上面例子中的二叉树，使用此方法遍历结果如下

//<888><444><222><555><111><999><666><333><777>

下图的红色和绿色箭头分别表示遍历深度的上升与下降

3.3.3 后序遍历（Postorder）

顺序是2在13之后（Post）被打印

  
template <typename X>
void BinaryTreeIterator<X>::TraversalPostOrder(X _node)
{
    //防止无限循环
    if (_node == nullptr)
        return;
    //打印顺序：左子--右子--自己
    TraversalPostOrder(_node->GetLeftChildPtr());
    TraversalPostOrder(_node->GetRightChildPtr());
    std::cout << "<" << _node->GetNodeData() << ">";
}

遍历同一二叉树的结果如下

//<888><444><555><222><999><666><777><333><111>

下图中紫色表示遍历的深度未变

3.3.4 三序遍历的总结

参考下图

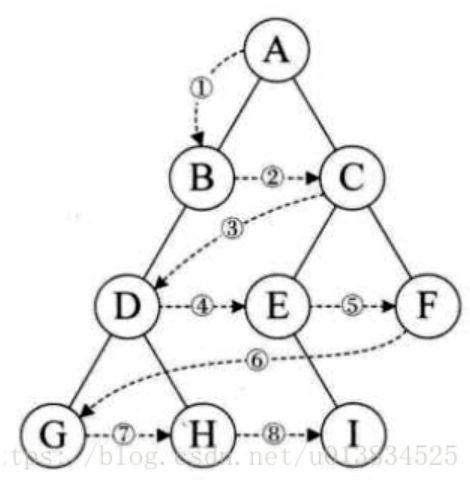
3.3.5 层序遍历（Levelorder）

前序遍历和DFS的效果一致，二叉树还有一种层序遍历的方式如下，效果与BFS一致

3.4 完满、完全、完美

3.4.1 如何区分

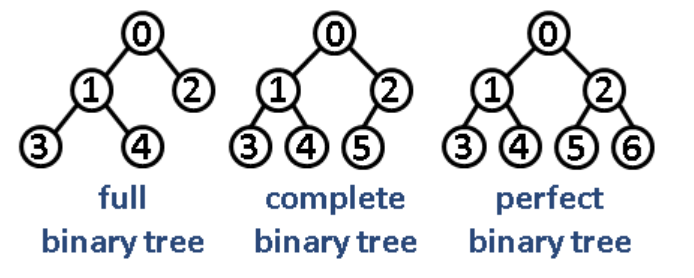
完满二叉树/满二叉树（Full Binary Tree）：除了叶节点外的每个节点都有两个子节点
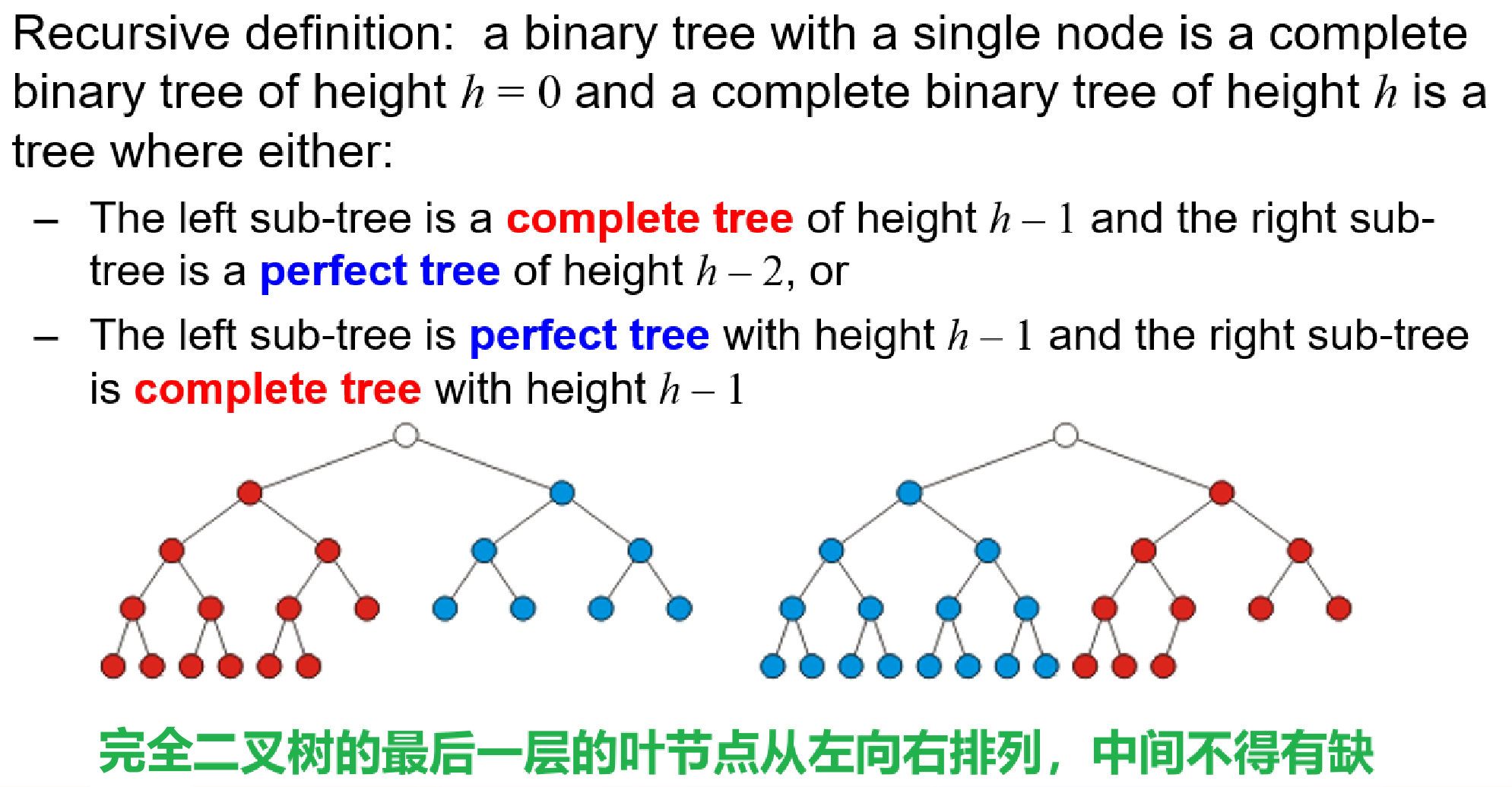
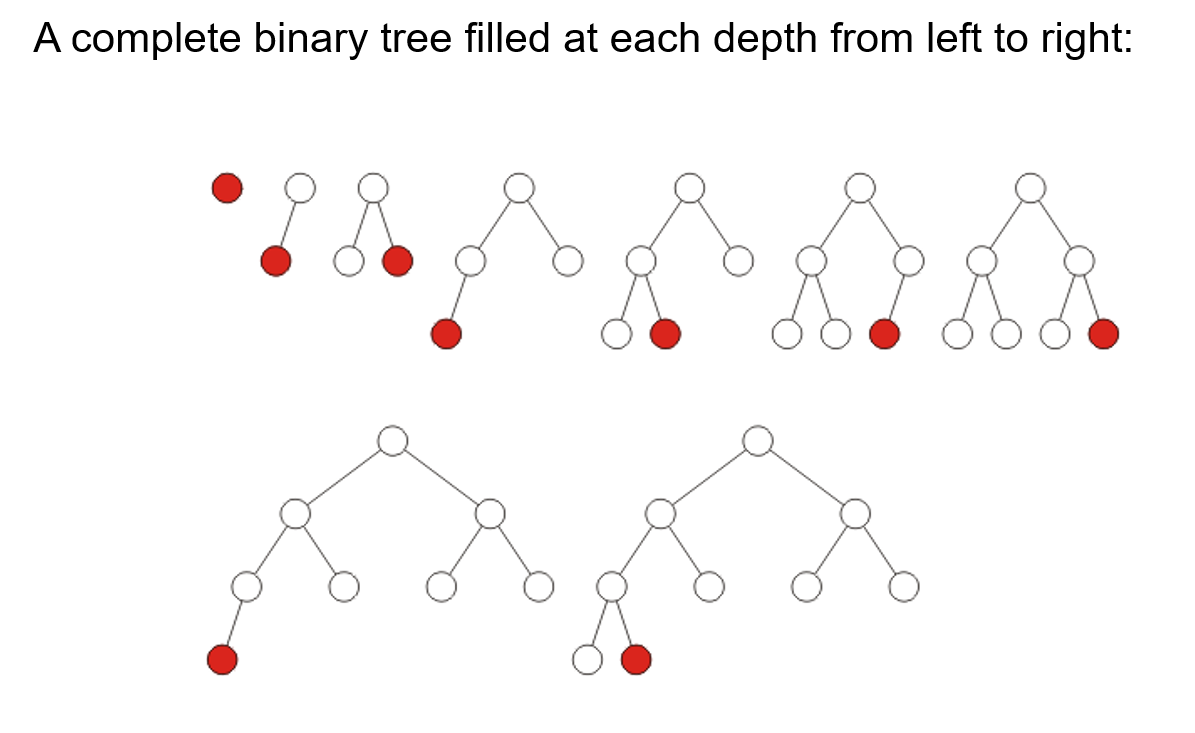
完全二叉树（Complete Binary Tree）：除了最后一层（叶节点全在同一层，即最后一层）之外的其他每一层都被完全填充，并且最后一层所有结点都保持向左对齐
完美二叉树（Perfect Binary Tree）：包含最后一层的每一层都被完全填充的完全二叉树，同时也是满二叉树

3.4.2 详解完美二叉树

3.4.2.1 表现形式

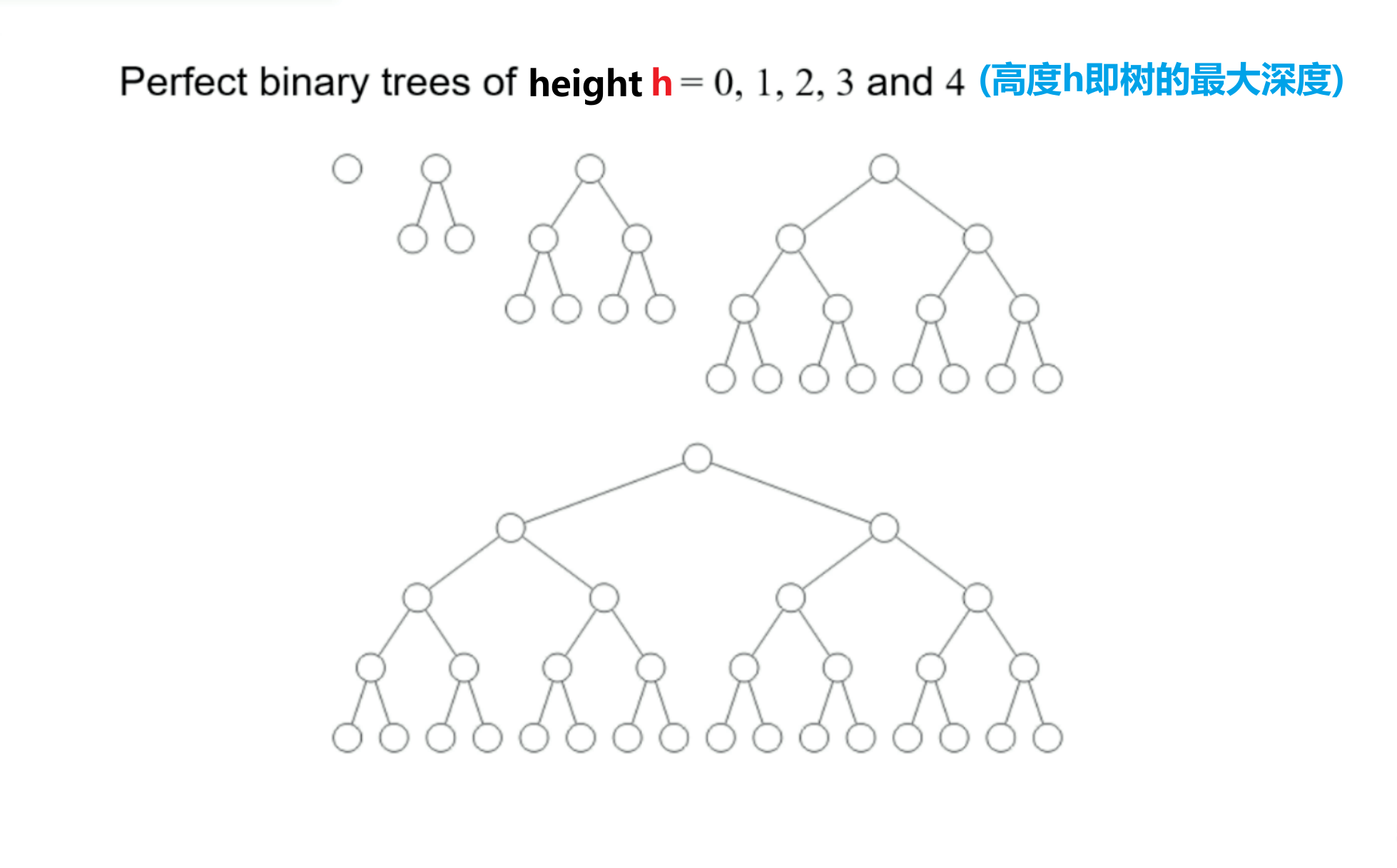
高度$h=0,1,2,3,4$的完美二叉树如下所示

3.4.2.2 高度与叶节点数的关系

一个高度为$h$（最小为$0$，此时只有根节点$1$个节点）的完美二叉树，其叶节点数为

\[2^h\]

3.4.2.3 高度与总节点数的关系

可以通过等比数列求和$\sum_{i=0}^{h}{2^i}=\frac{2^0\cdot(1-2^{h+1})}{1-2}$计算得拥有的节点数总共为

\[n = 2^{h+1}-1\]

解方程$n=2^{h+1}-1$得在已知二叉树为完美二叉树时，树高度与其节点数的关系为

\[h=\log_{2}{(n+1)}-1\]

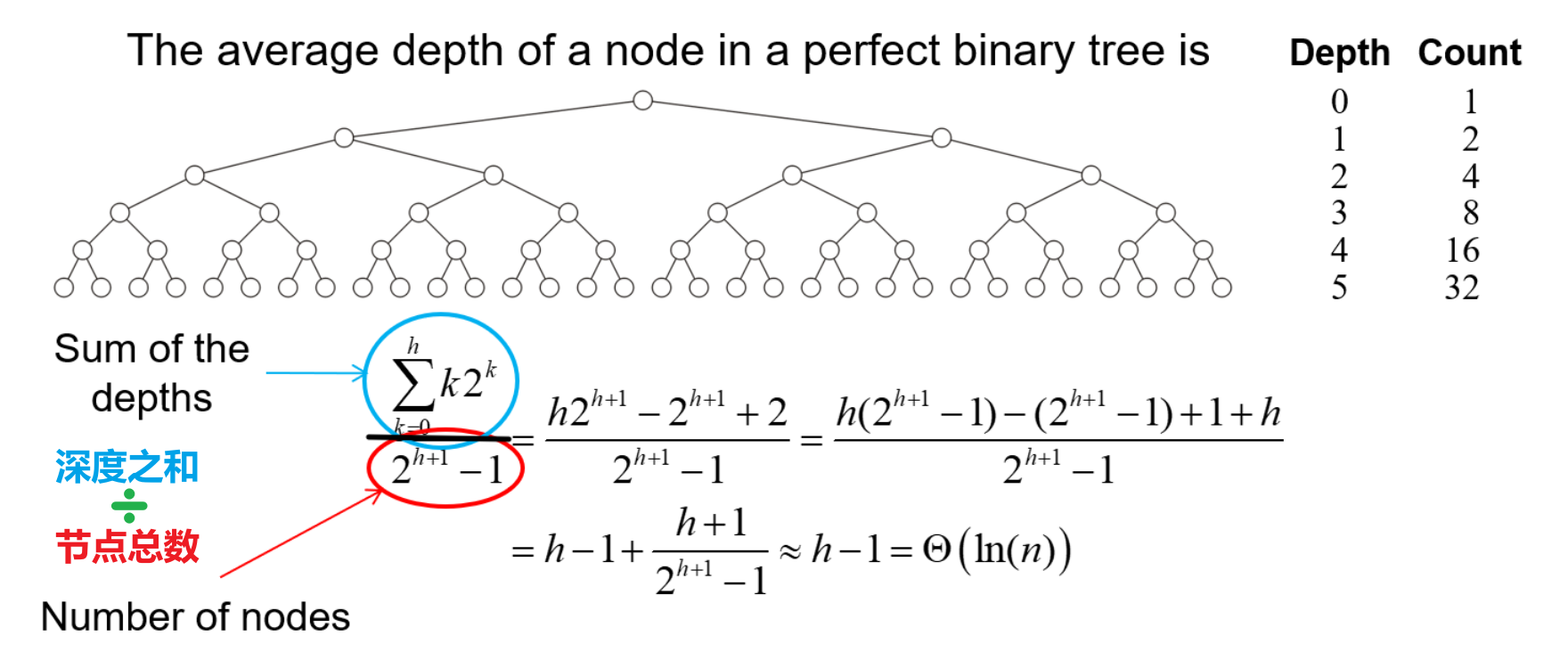
3.4.2.4 平均深度

完美二叉树的每个节点的平均深度约等于$h-1$，其中$h$为高度，即最大深度

3.4.3 详解完全二叉树

3.4.3.1 递归定义

完全二叉树的递归定义如下

3.4.3.2 高度与节点数的关系

在后续讨论时间复杂度的部分，我会详细推导节点数为$n$的二叉树的最小高度，这相当于在已知完全二叉树的节点数的条件下求其高度

\[h = [\log_{2}{n}]\]

3.4.3.3 线性表实现

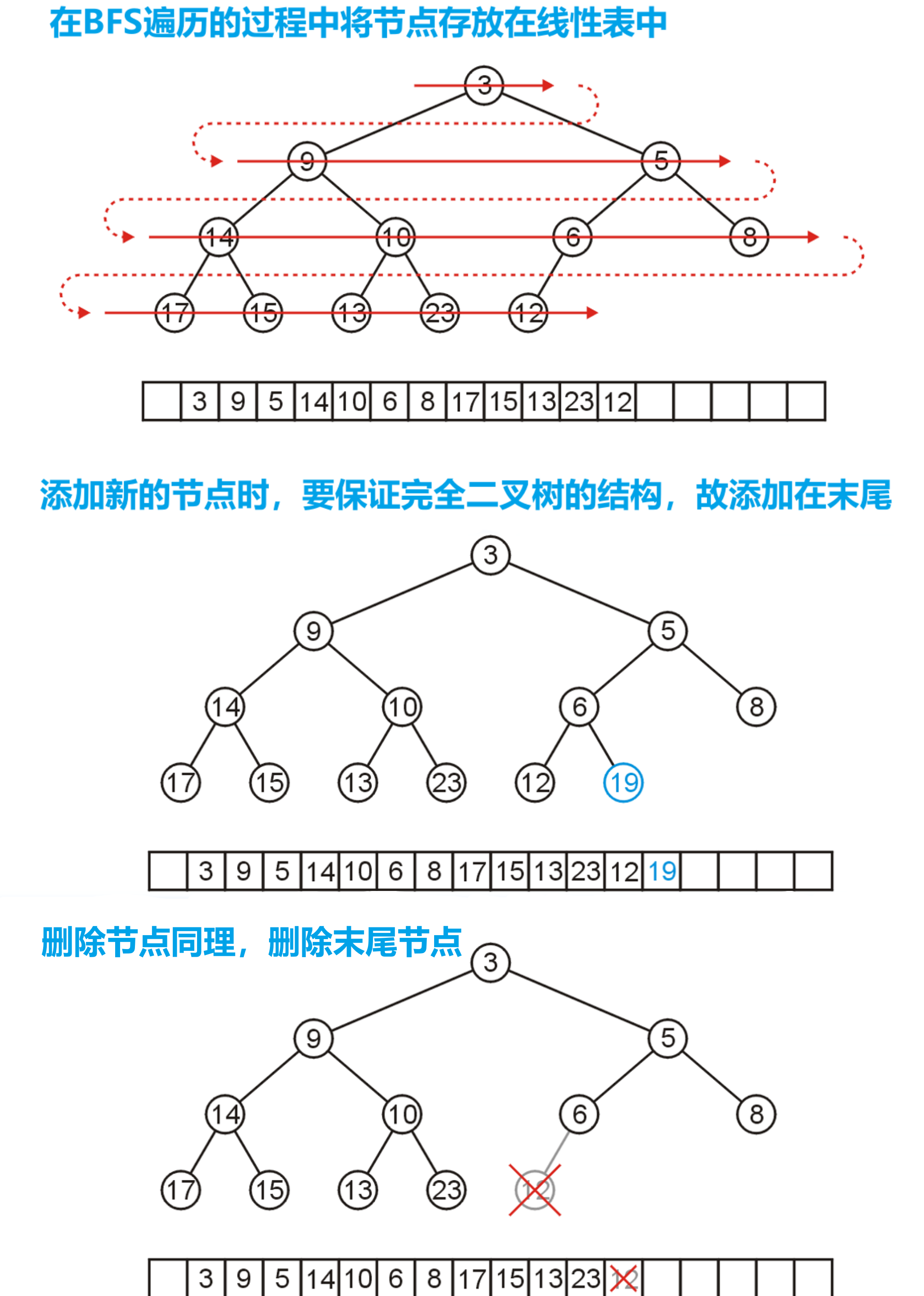
从根节点开始构造完全二叉树的顺序，和BFS遍历（从左往右）的顺序一致

所以我们可以将完全二叉树的各个节点以BFS的顺序存放在线性表中

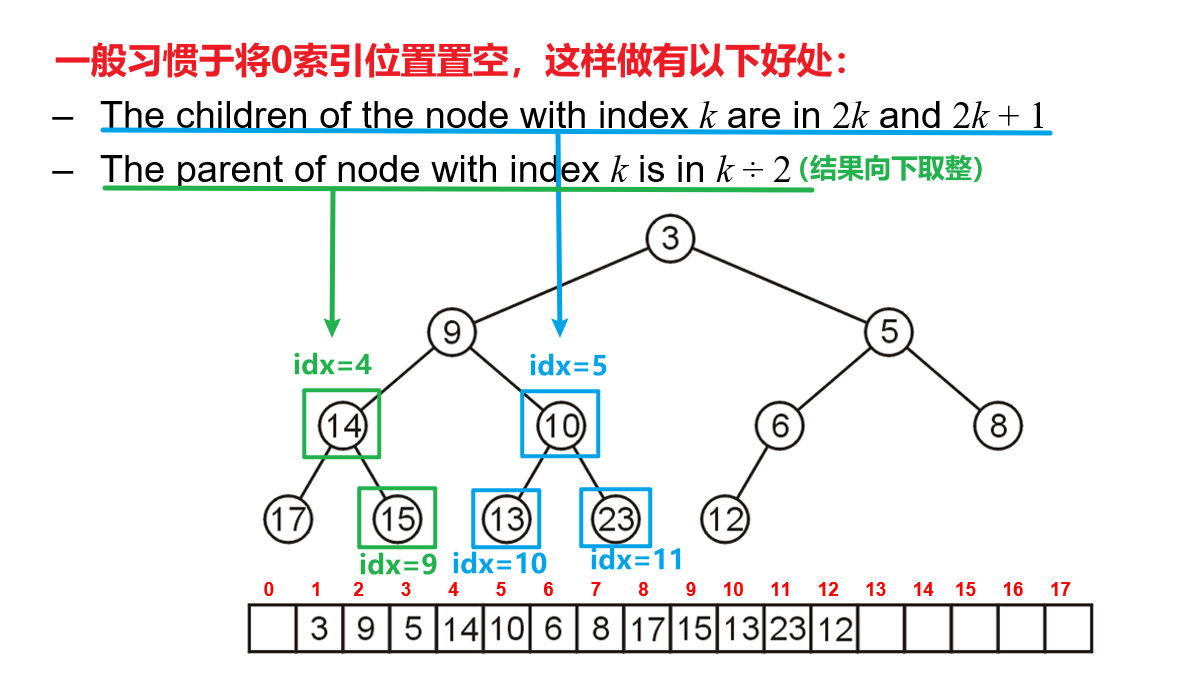
注意到我们将线性表的0索引位置空出，这是为了可以通过对某节点的索引值的计算，更方便地找到其父或子节点（在代码中可以直接通过公式计算以获取父子节点在线性表中的索引，而无需通过设计一个树结构并通过指针维护父子关系）

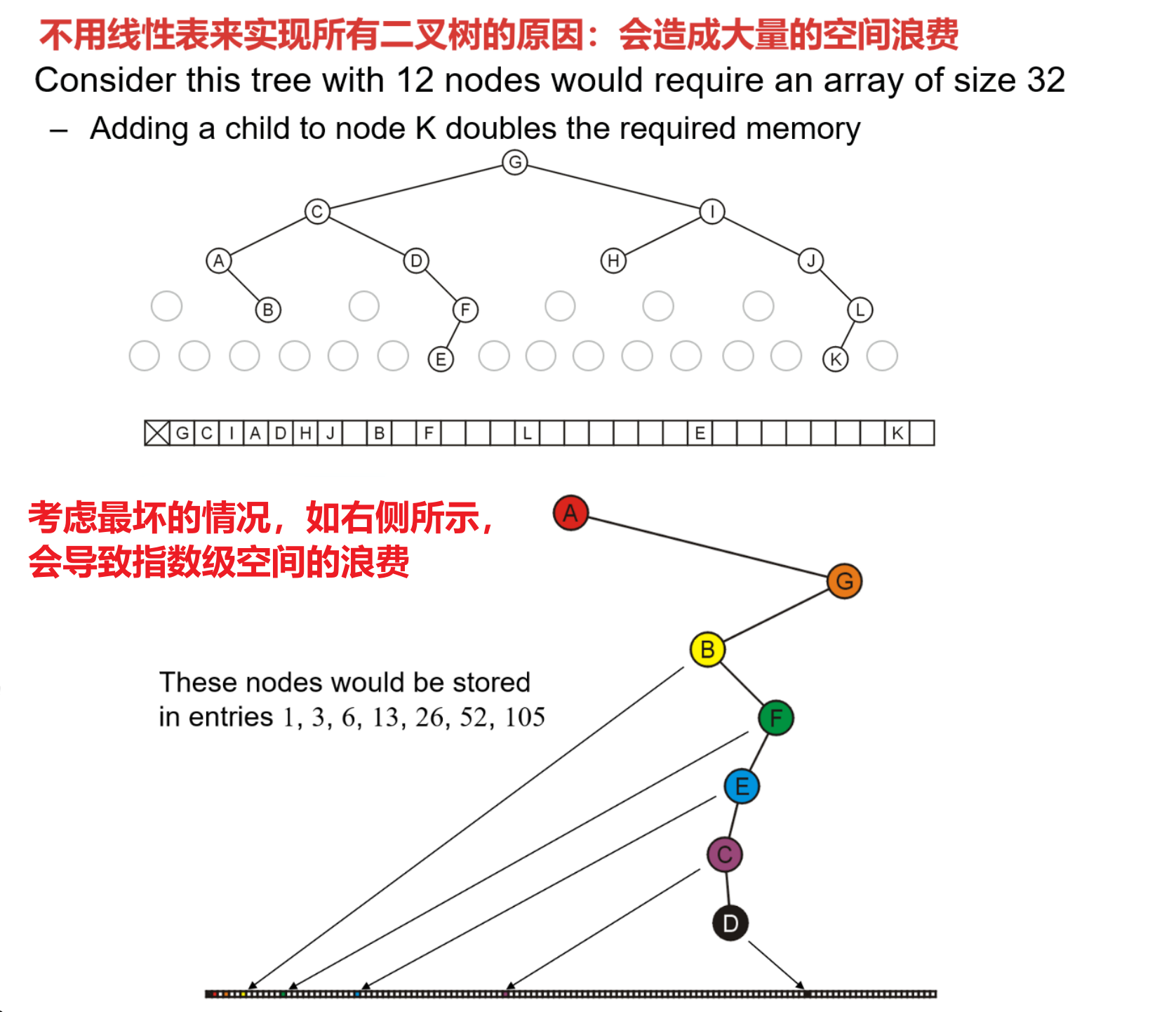
对比来看，我们之所以不用线性表实现所有二叉树，是因为完全二叉树对线性表空间的利用充分，其它二叉树若使用线性表实现，则会造成大量的空间浪费

3.5 时间复杂度

此处分析针对的其实是二叉搜索树，其搜索的复杂度与高度有关

3.5.1 定节点数的二叉树高度

如果每次给二叉树增加新结点的时候，都朝着构造完美二叉树（其定义详见相关章节笔记）的方向添加，那么就可以使得该$n$节点的二叉树的高度（高度就是树的最大深度）最小，即构造一棵完美或类完全二叉树（叶节点不一定都从左到右无缺排列）时，其高度最小，如下所示
- $n=1$时，$h=0=[\log_{2}{1}]$，（$[x]$表示向下取整）
- $n=2,3$时，$h=1=[\log_{2}{x}],\space x\in {2,3}$
- $n=4,5,6,7$时，$h=2=[\log_{2}{x}],\space x\in {4,5,6,7}$
- 所以对于任意$n$，$h=[\log_{2}{n}]$
反之若想使二叉树的高度最大，那就将其退化为链表，此时$n$节点的二叉树链表的长度就是$n$，也即此时其高度为$h=n-1$

3.5.2 访问单个元素的时间复杂度

我们想要访问（查找、插入、删除等）二叉树中的某个节点时（类比访问链表元素），所需耗费的时间复杂度与树的高度（类比链表的长度）有关，而$n$节点的树的高度与其树的结构有关
- 最坏的情况，即退化为链表的二叉树：$O(n)$
- 最优的情况，即接近于完美的二叉树：$O([\log_{2}{n}])=O(\log_{}{n})$，由于时间复杂度不考虑时间函数的最高次项的系数，所以此处的$\log$的底可以任取
- 平均的情况：$O(\sqrt{n})$，没太搞懂是怎么算的

3.5.3 遍历二叉树的时间复杂度

递归地遍历所有节点，其时间复杂度如下算式所表示

\[T(n)= \left\{ \begin{aligned} O(1),\space\space\space\space\space\space\space\space\space n=1\\ 2T(\frac{n}{2})+O(1),\space n>1 \end{aligned} \right .\]

根据主定理可得，时间复杂度为$O(n)$

3.6 二叉树的应用

3.6.1 哈夫曼编码（Huffman Code）

参考此博客以及此题解

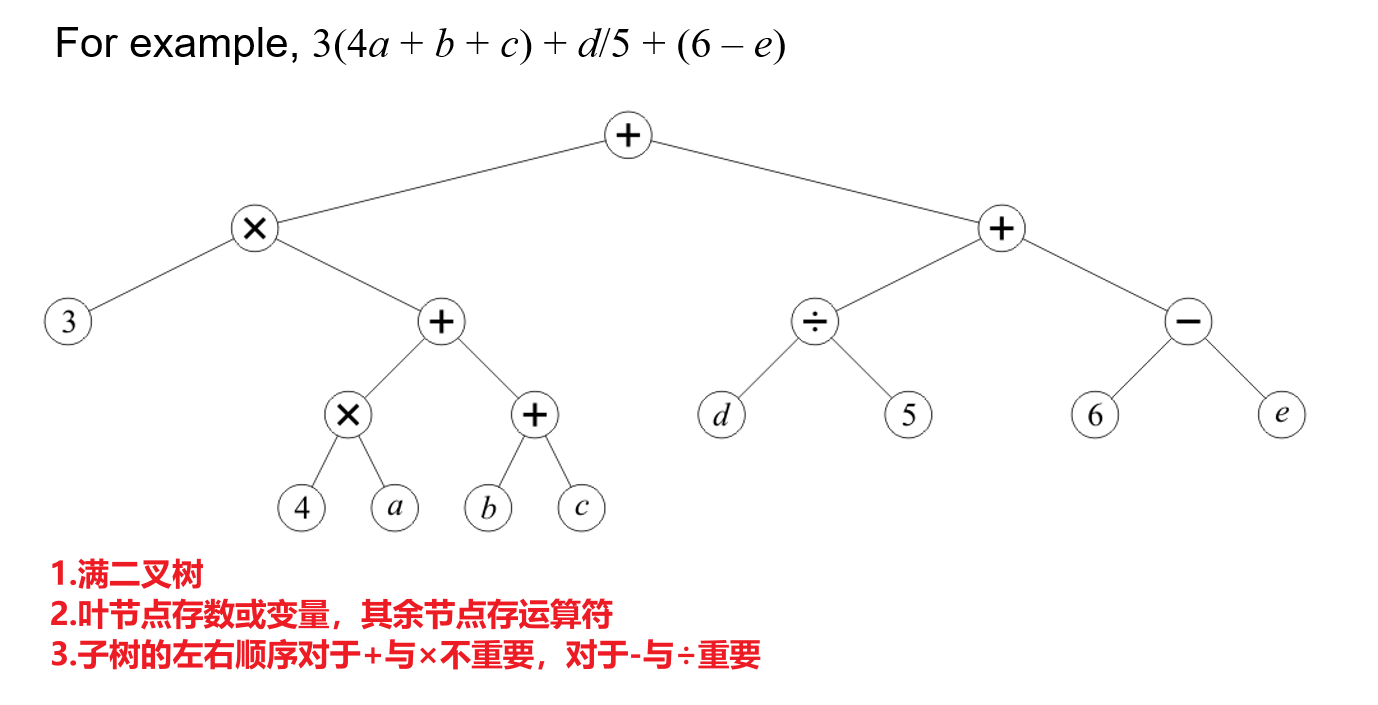
3.6.2 算式树（Expression Tree）

二叉树用于计算算式

四、N叉树

N叉树（N-ary Tree）并不意味着树节点可以有任意数量的子树，而是和二叉树一样，对子节点的最大数量限制为N个

4.1 形式示例

三叉树（3-ary Tree, Ternary Tree）的每个节点最多有三个子树（子节点）

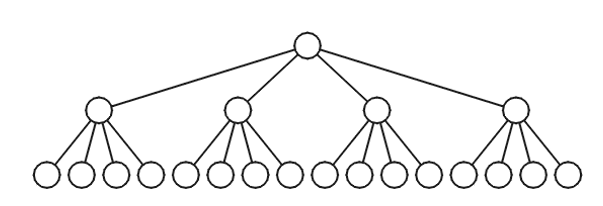
四叉树（4-ary Tree, Quaternary Tree）同理，下图是完美四叉树

4.2 完美N叉树

完美N叉树的节点数量与其高度的关系为（依然是等比数列求和）

\[\begin{aligned} &n=\sum_{i=0}^{h}{N^i}=\frac{N^{h+1}-1}{N-1} \\ &h=\log_{N}{(n(N-1)+1)}-1 \end{aligned}\]

视$N$为常数，当变量$n\rightarrow\infty$时，$h$等价于$log_{N}{(n)}$，即二者之比取关于$n$趋于无穷的极限为$1$，则我们可以得知在节点总数相同的条件下，完美N叉树与完美二叉树的高度之间的倍数关系为

\[\frac{h_2}{h_N}=\frac{log_{2}{(n)}}{log_{N}{(n)}}=\log_{2}{N}\]

例如同样的总节点数，完美四叉树的高度近似为完美二叉树的$\frac{1}{2}$，完美十六叉树的高度则为完美二叉树的$\frac{1}{4}$

4.3 完全N叉树

完全二叉树的高度为$h = [\log_{2}{n}]$，推广到N叉树就是

\[h=[log_{N}{(n(N-1))}]\]

完全N叉树同样可以用线性表实现（注意下图没有像二叉树那样把线性表的$0$索引处置空）

4.4 代码实现

可以像我之前实现TreeNode<T>类那样实现，在AddChild等函数中对子节点数量进行限制即可，但这种方式的子节点链表需要动态申请内存（从0开始到N）
下面是另一种可能的方式，这种方式在编译时就申请了固定容量的线性表容器，而无需动态申请内存，且无需手动析构（如果使用NaryTree *children[std::max(N, 2)]申请的话），具体实现我就不写了

  
//使用模板初始化N叉树时传入存储的数据类型T与叉数N
template <typename T, int N>
class NaryTree
{
private:
	T nodeData;
	//初始化容积为N的固定容量线性表容器
	SequentialList<NaryTree> children(std::max(N, 2));

public:
	NaryTree(T const& = T());
	//...
};

五、二叉搜索树

5.1 产生背景

设想我们要实现一种有序列表（Sorted List），其除了满足基本的线性表功能外，还被要求满足以下功能方法
- 查找列表中值最小/最大的元素，返回其索引
- 查找列表中$n^{th}$大的元素，返回其索引
- 查找列表中比传入元素（需检测是否在列表中）大的下一个元素，返回其索引
- 遍历列表中元素值在区间$[a,b]$内的元素
如果我们在链表或数组内实现这样的功能，那么对$n^{th}$位元素各种操作的复杂度就会是$O(n)$，因为各种大小的元素的位置是不确定的
设想一种二叉树，其任意节点的左子节点在数值上总是比自己的小，自己在数值上总是比右子节点的小，值相同的话则无所谓顺序；我们将元素存储在这样的二叉树内，我们想要查找某个值的索引时，就将其与根节点对比，自己小就往左子节点递归搜索，大就往右子节点递归搜索，这样就使得我们按照大小对值的搜索就不是无序的了

5.2 形式定义

二叉搜索树（Binary Search Tree）是一种满足如下性质的非空二叉树：
- 左子树（如果存在）是二叉搜索树，且其任意后代节点（包括自身）的值小于根节点
- 右子树（如果存在）是二叉搜索树，且其任意后代节点（包括自身）的值大于根节点
二叉搜索树的节点存储的数据应当是可以用于比较大小的类型（也就是说自定义数据类型需要重载各种比较运算符），并且除了特别说明，一般不会存储两个相同的数据，实际应用中也很少会出现需要将同一个数据值分为多个实体存储的需求
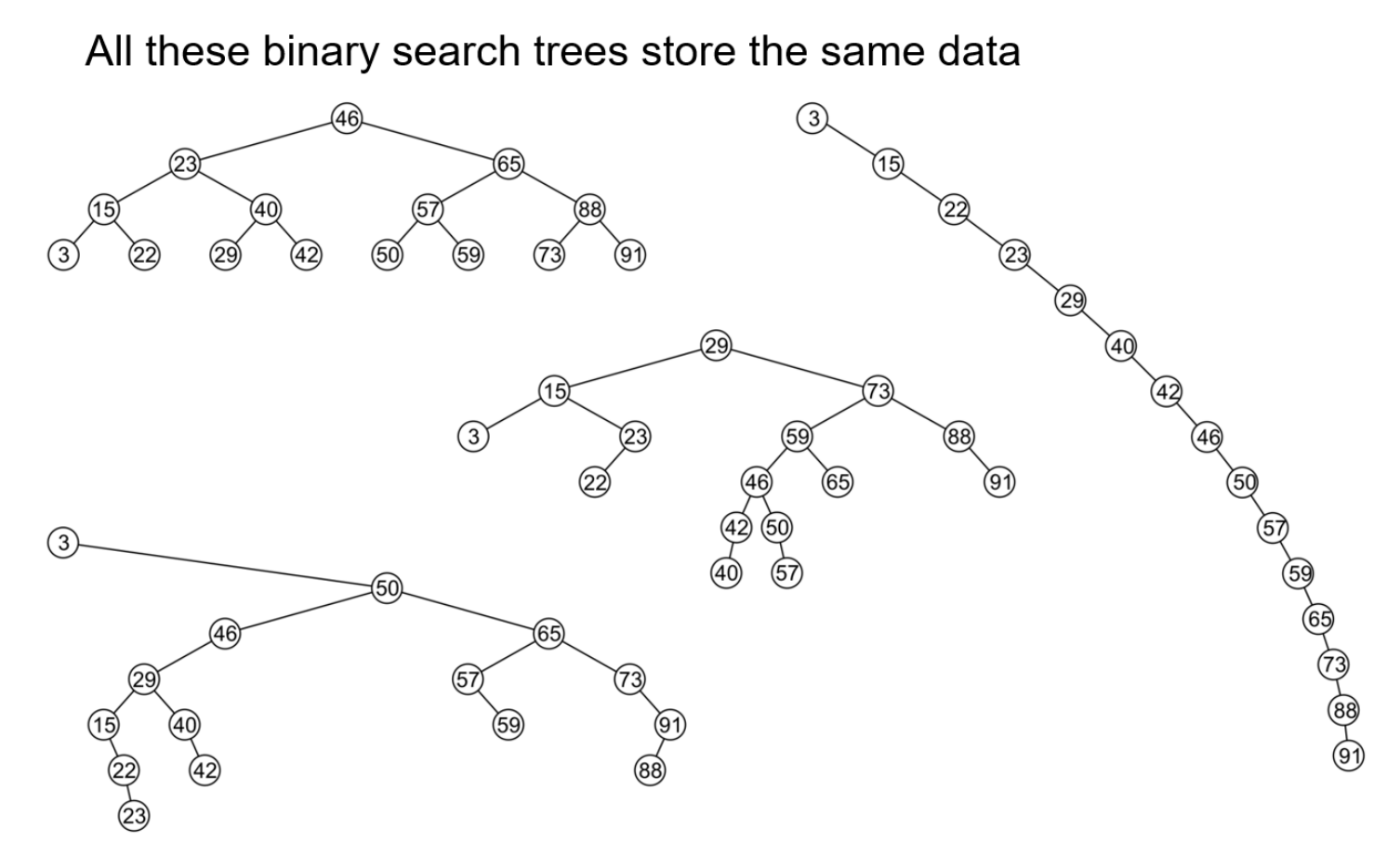
如下图所示，可以看出对于同一颗二叉搜索树，若根节点不同，则会产生不同的排列结果；并且在根节点确定的情况下，依据插入顺序的不同，搜索树的形状也会有所不同

当根节点的值是整个树中最小的时，二叉搜索树就退化（Degenerate）为链表，导致其时间效率上的优势丢失殆尽

5.3 值的查找

5.3.1 极值的查找

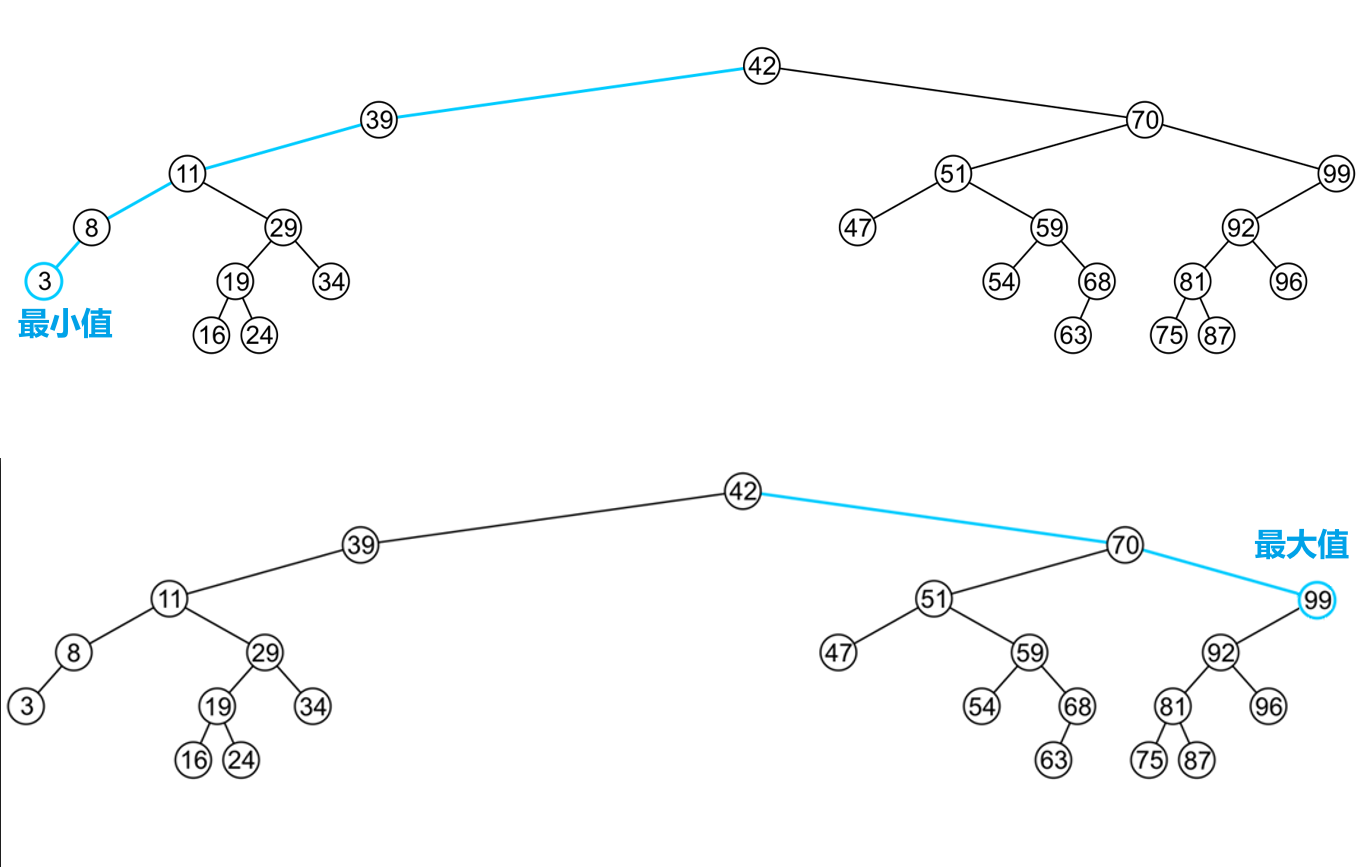
查找最小或最大值，只需找到最左或最右侧的节点（不一定是叶节点）即可

搜索的时间复杂度为$O(h)$，其中$h$为树的深度（即最差的情况下要遍历的节点数，时间复杂度就取决于最费时的情况）

5.3.2 查询特定值是否存在

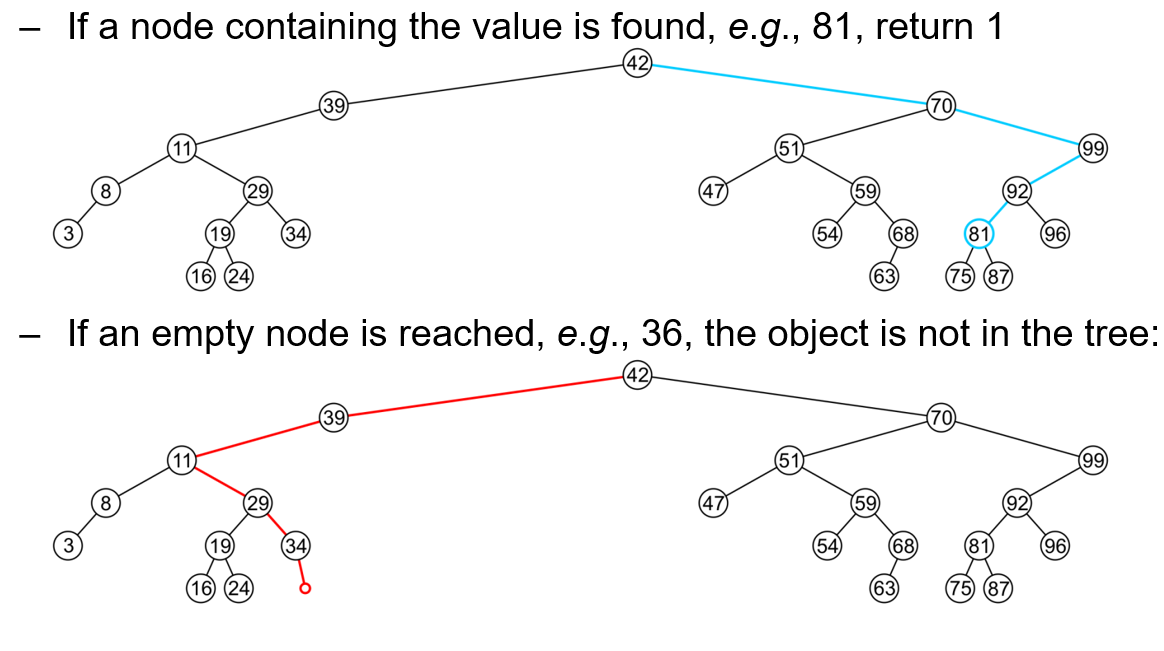
若想要直到某一个特定的值是否存在于二叉搜索树中，则不断递归调用这个查询函数自身即可
- 对比目标值与被查询节点自身的值的关系，若目标小于后者，则递归查询后者的左节点；若目标大于后者，则递归右节点
- 直到某次递归调用接收的目标值等于传入节点的值，则目标值存在于最搜索树中
- 直到某次递归调用接收的或者传入节点为空指针，则目标值不存在于搜索树中

5.3.3 查找相邻值与特定位置的值

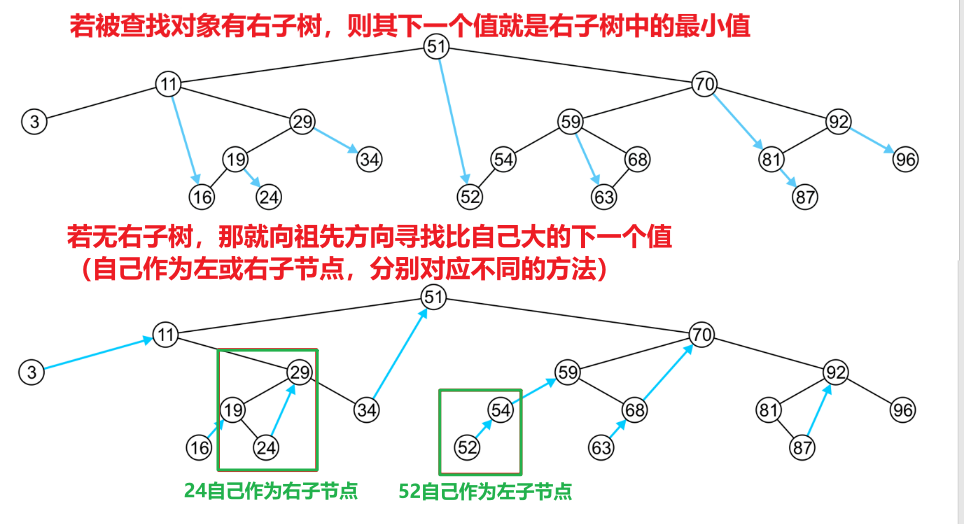
若想按照大小顺序，查找某个值的下一个（比自己大的）值是多少，就用下面的方法

若想查找某个值的前一个（比自己小的）值，类比上述方法即可

5.3.4 查找特定大小顺序的值

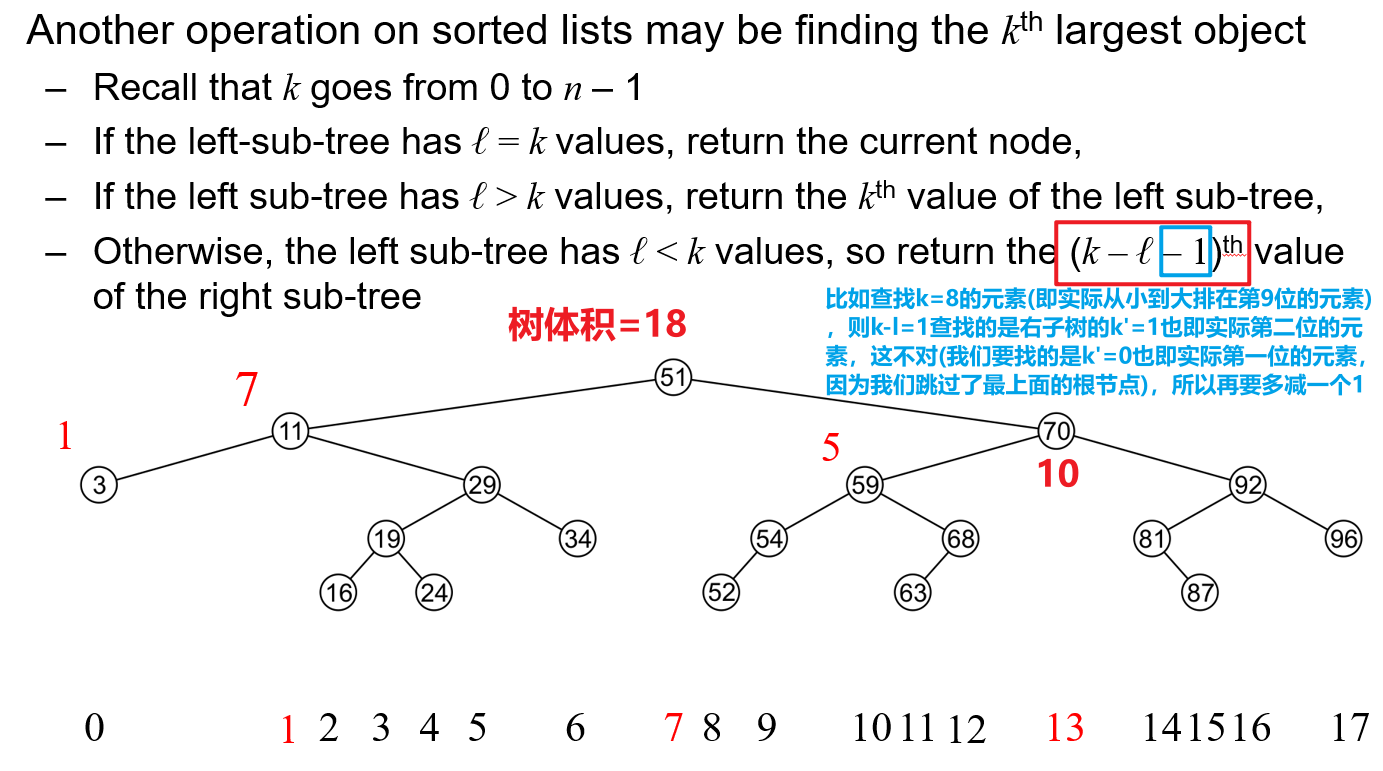
如果想以索引$k$查找搜索树中从小到大排在$(k+1)^{th}$的值（整数$k$在范围$[0,n-1]$内，相当于访问线性表中索引为$k$位置的元素值，且该线性表的所有值从小到大排列），则采用以下算法
- 如果搜索树的左子树的体积$Size(left)=k$，则该树根节点的值就是目标值
- 如果$l>k$，则说明目标值在左子树中，递归用此方法查找左子树的$k^{th}$值即可
- 如果$l<k$，则说明目标值在右子树中，则递归查找右子树的$(k-l-1)^{th}$值即可，至于多减去一个$1$的原因，详见下图的文字注释

5.4 值的插入

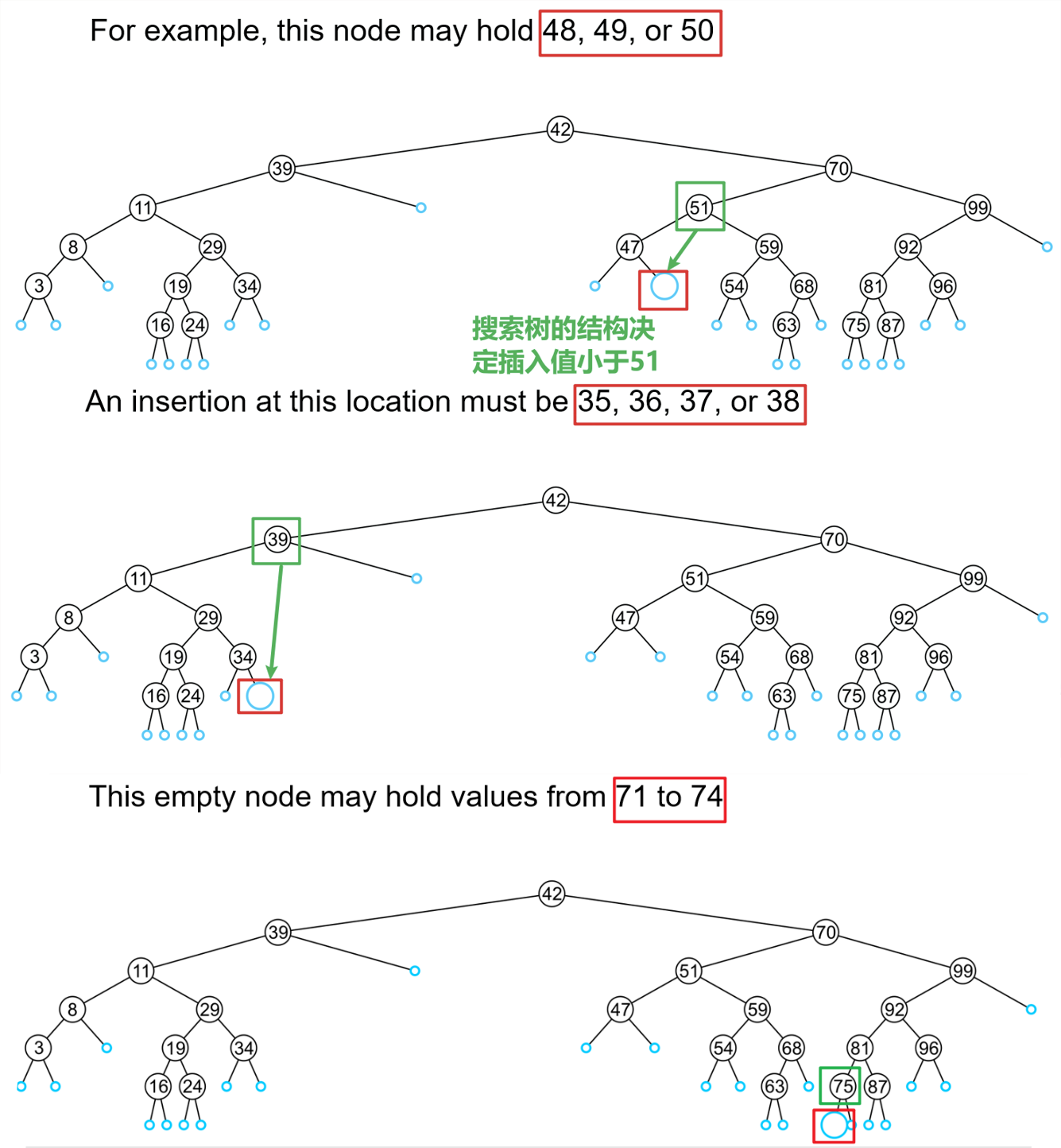
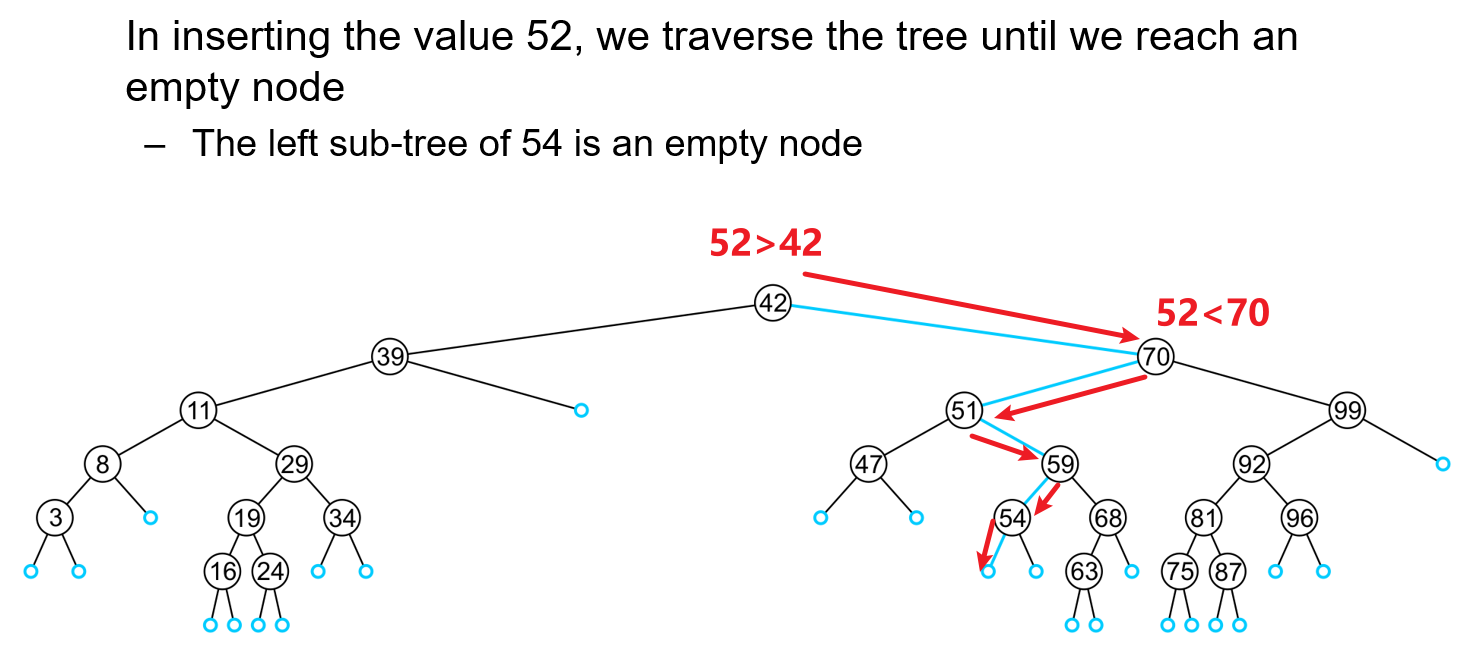
可以观察到，新的值的插入只会发生在搜索树的叶节点上

从根节点开始一一比较大小即可，直到遍历到空节点，就将插入值新建在该位置即可（若是遇到相等的值，无需额外新建一个新的等值子节点，直接return即可）

5.5 值的删除

5.5.1 存值的是叶节点

这种情况下，直接删除，并把被删除对象的对应子节点设置为nullptr即可

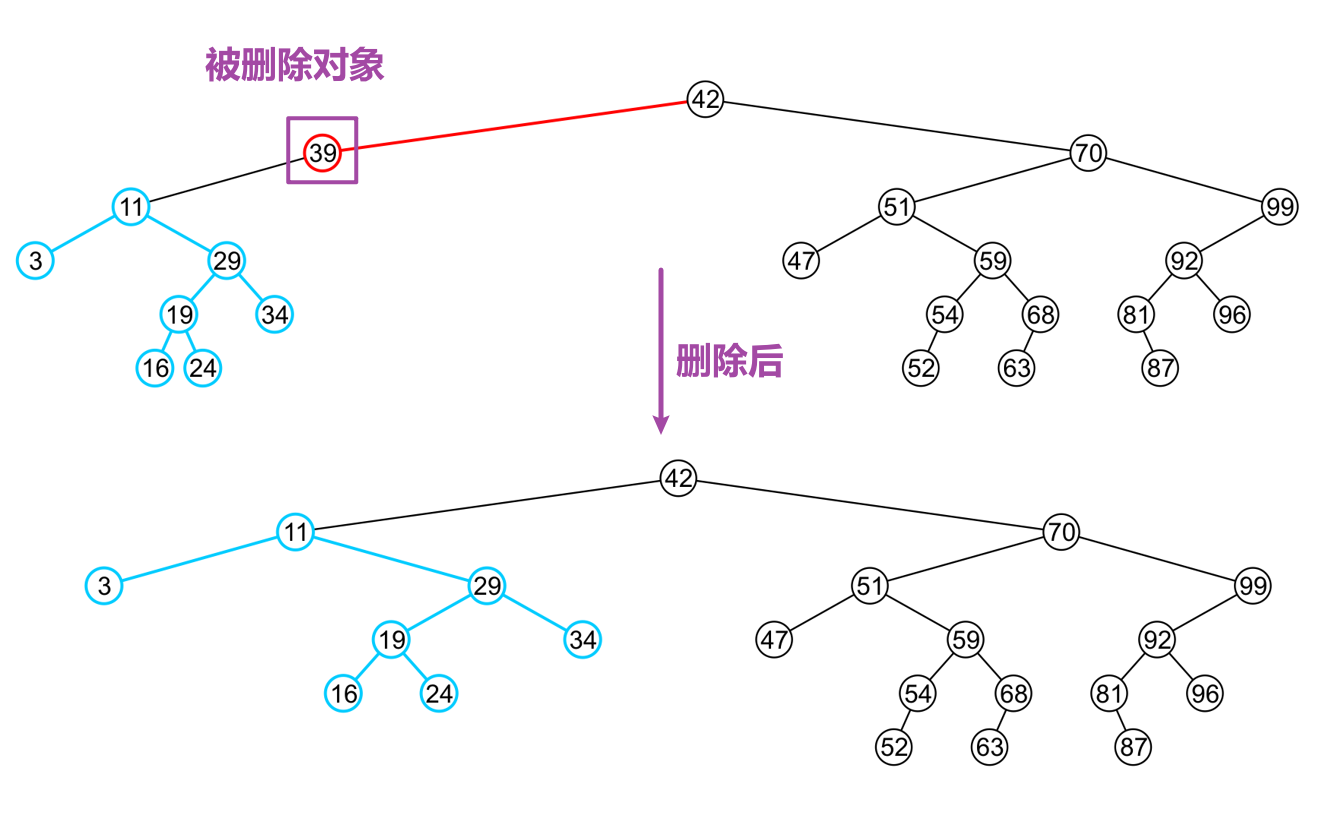
5.5.2 存值的是有一个子节点的内部节点（或根节点）

这种情况下，用被删除对象的子树代替自己的位置即可，然后将自己删除

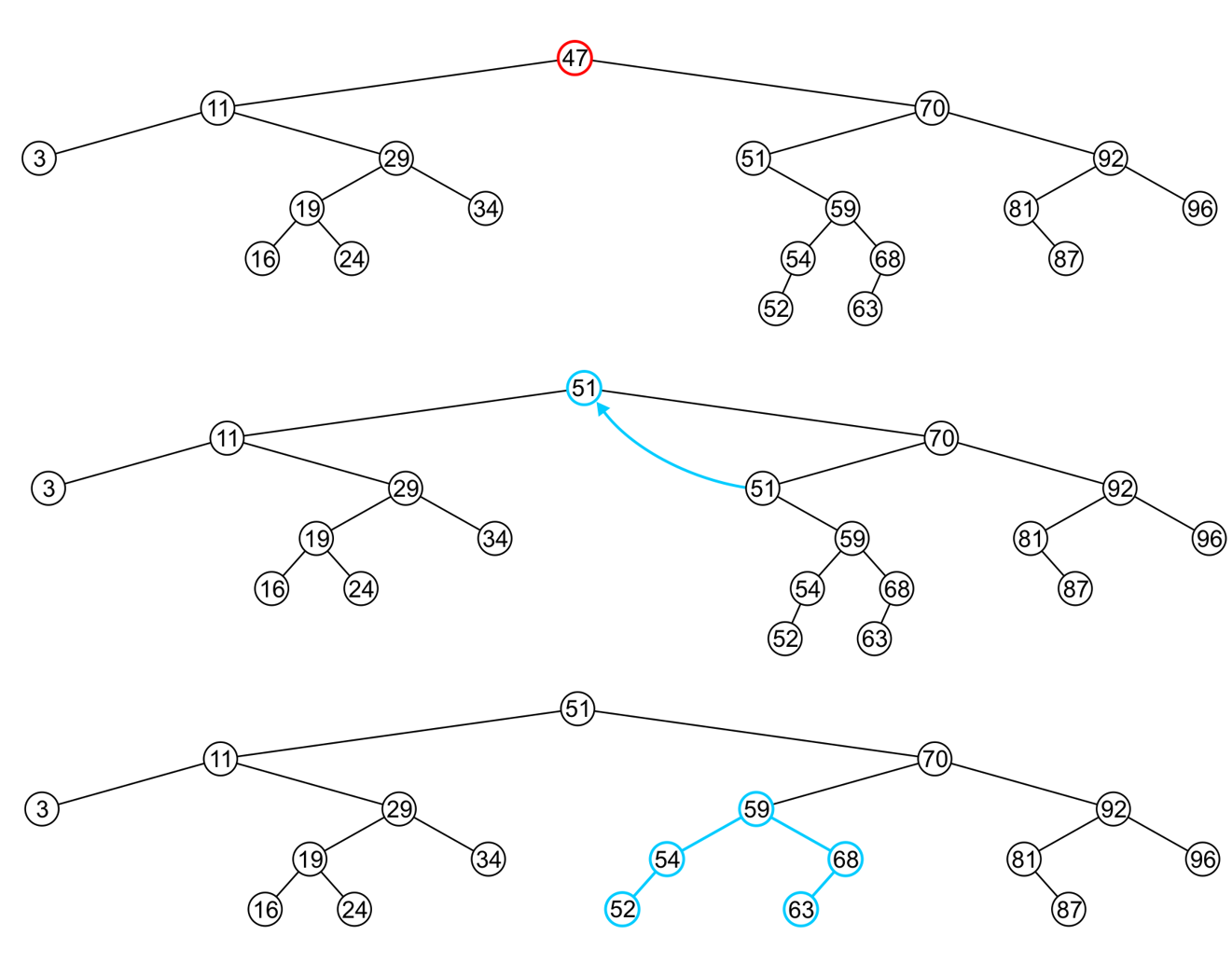
5.5.3 存值的是有两个子节点的内部节点（或根节点）

这种情况下，把右子树上最小值转移到自己的位置上来代替自己即可

继续删除，这时候的情况稍比上一种复杂一些，在实现的时候两种情况都需要被考虑到

5.6 代码实现

具体的实现参考项目仓库

  
//二叉搜索树类，使用组合而非继承的方法包装着一个二叉树节点，不支持存储相同数据的节点
template <typename T>
class BiSearchTree
{
private:
    BinaryTreeNode<T>* root;               //维护一个二叉树节点内核

public:
    BiSearchTree();                        //构造函数，无=或构造的重载函数
    ~BiSearchTree();                       //析构函数，清空搜索树

    bool IsEmpty() const;                  //判断搜索树是否为空
    void PrintTree() const;                //打印整个搜索树
    T FindMin() const;                     //返回存储的最小值
    T FindMax() const;                     //返回存储的最大值
    T FindFormer(const T&) const;          //寻找树中比传入值小的相邻值
    T FindLatter(const T&) const;          //寻找树中比传入值大的相邻值
    T FindByIdx(int) const;                //以索引k获取树中从小到大排在第(k+1)位的值
    bool Contains(const T&) const;         //查找是否存在某个节点

    void Insert(const T&);                 //直接将新的节点插入正确位置
    void Erase(const T&);                  //以值删除某个数据节点
    void MakeEmpty();                      //清空搜索树

private:
    BinaryTreeNode<T>* FindMinPtr(BinaryTreeNode<T>*) const;
    BinaryTreeNode<T>* FindMaxPtr(BinaryTreeNode<T>*) const;
    T FindFormer(const T&, BinaryTreeNode<T>*) const;
    T FindLatter(const T&, BinaryTreeNode<T>*) const;
    T FindByIdx(int, BinaryTreeNode<T>*) const;
    bool Contains(const T&, BinaryTreeNode<T>*) const;

    void Insert(const T&, BinaryTreeNode<T>*);
    void Erase(const T&, BinaryTreeNode<T>*);
    void MakeEmpty(BinaryTreeNode<T>*);
};

5.7 时间复杂度

上述提到的二叉搜索树的几乎所有操作的时间复杂度都是O(h)，即高度$h$决定时间效率，因为二叉搜索树不会遍历每一个分支，而是依靠对值的比较来唯一确定一个分支进行深入搜索
- 最糟糕的情况为$h=n$时（二叉树退化为链表），时间复杂度$O(n)$
- 最优情况为搜索树为$h=[\log_{2}{n}]$时（搜索树为类完全/完美二叉树），时间复杂度$O(\log{n})$

学科笔记, 数据结构

数据结构 C++

本文由作者按照 CC BY-NC-SA 4.0 进行授权