半通关《图灵完备》后的思路整理与反思

一、写在前面

1.1 游玩契机

• 前两天我看见同学在Steam上玩《Turing Complete》，此前我对数字电路的了解也仅仅是Minecraft的红石电路，想到玩了那么多年的MC我却只会抄别人的投影，我自愧不如，便一怒之下买了一份《图灵完备》来玩一玩

• 题外话：在这个游戏里排线时，我总感觉有种在玩RTS游戏《Mindustry》的既视感，后者的元器件种类数量十分庞大，各种线路排布很容易乱套

• 爆肝三天后终于勉强通了别人随手就能解开的关卡

1.2 玩后反思

你问我为什么把总结写在文章开头？因为我不自信读者能读完我的文章直到结尾，哈哈

• 我这学期开始学计算机组成原理了，课上课后学到了很多底层一点的知识，但看着课件上那些抽象的硬件结构和数字逻辑电路图时，总感觉一阵头晕，隐隐对这些东西产生了一些抗拒心理

• 在心思没那么成熟的时候（现在大抵也不那么成熟），我时常思考：作为程序员/工程师，我为什么要学习这些如此底层的东西，只要把代码写好了不就可以了？在学习计组前，我已经浅浅写过了两三个复杂度较高的工程项目，导致我有点将高级语言以及工具软件的强大力量错误地归因成自己的某种能力了

• 当我在游戏的优秀引导下，一步步从最基本的逻辑门电路搭建出从1bit到3bit的解码器、从1bit的锁存器到8bit的寄存器、ALU、COND，再到用这些自己搓出来的轮子造出一个最简单的图灵完备的处理器，再到用指令集操纵其内寄存器写出最简单的汇编程序的时候，给我带来的成就感不亚于自己用高级语言写出一个勉强能跑的游戏

• 请原谅我认知水平尚浅，所学知识大都一知半解，无法得出更专业而深入的思考，但我在玩了这个游戏之后突然就明白作为程序员/工程师，为何要学习底层硬件的知识了：计算机就是最伟大最优美的工程之一，而学习计算机的底层知识或许就是培养工程思维的好方法之一

二、第I章：基础逻辑电路

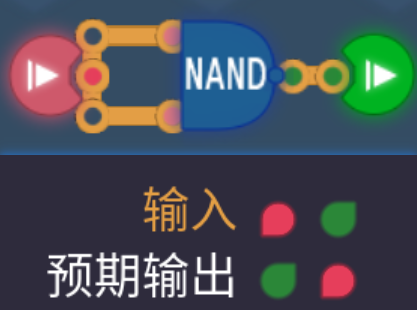
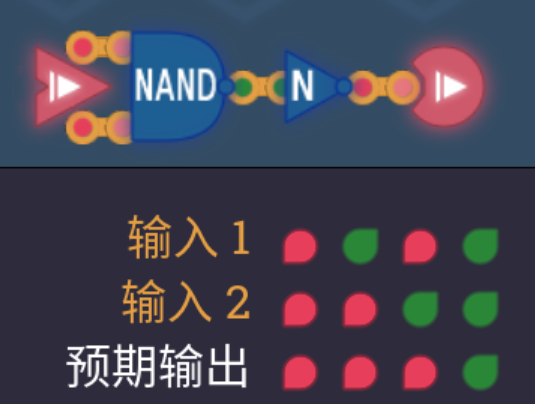
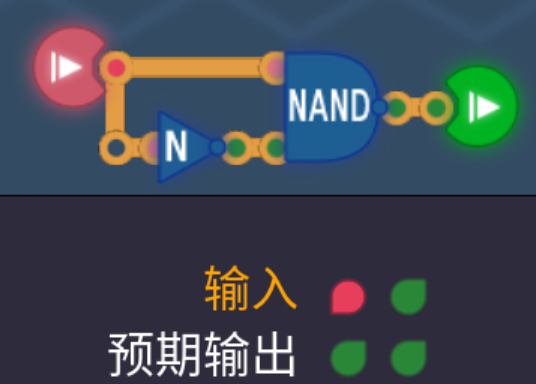
2.1 与非门NAND

• 与非门真正的含义其实是”非与门”，其真值表的最后一行和与门的真值表最后一行完全相反
• 使用NAND或者是NOR（或非门）可以构建出任何一种其它逻辑门，所以二者被称为通用门

2.2 非门NOT

• 通过NAND我们可以实现1bit非门，其可以将所有输入信号取反进行输出

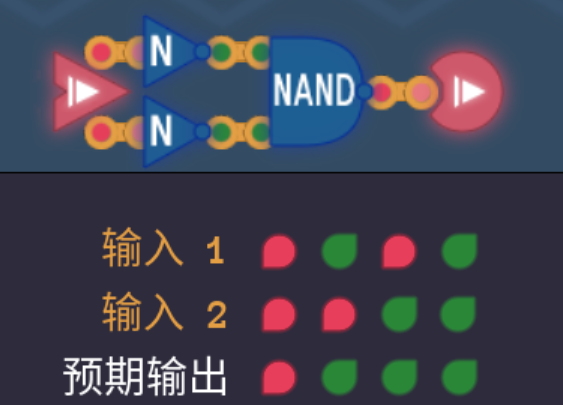
2.3 与门AND

• 我们将NAND的输出取反即可得到AND

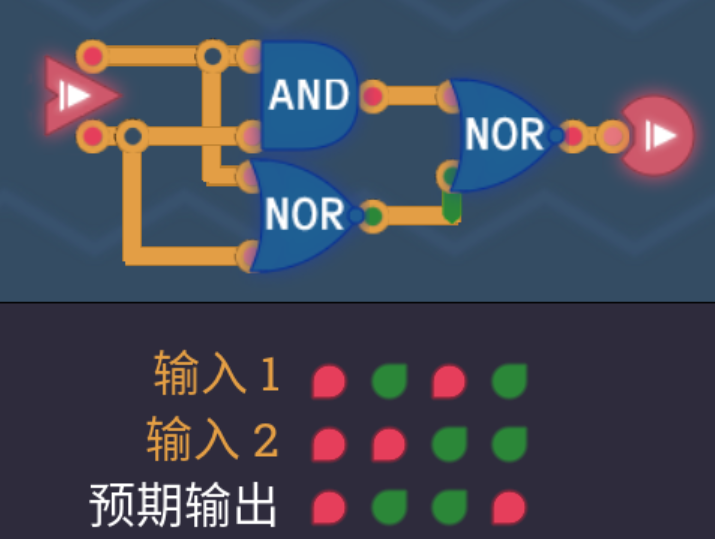
2.4 或非门NOR

• 将AND的输入输出全部取反即可

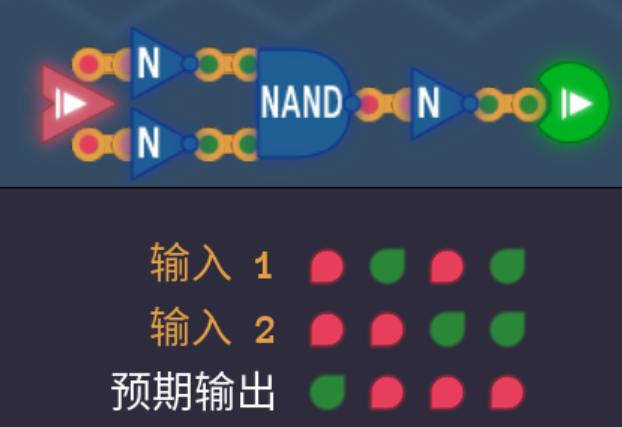
2.5 或门OR

• 将NAND的输入输出全部取反即可

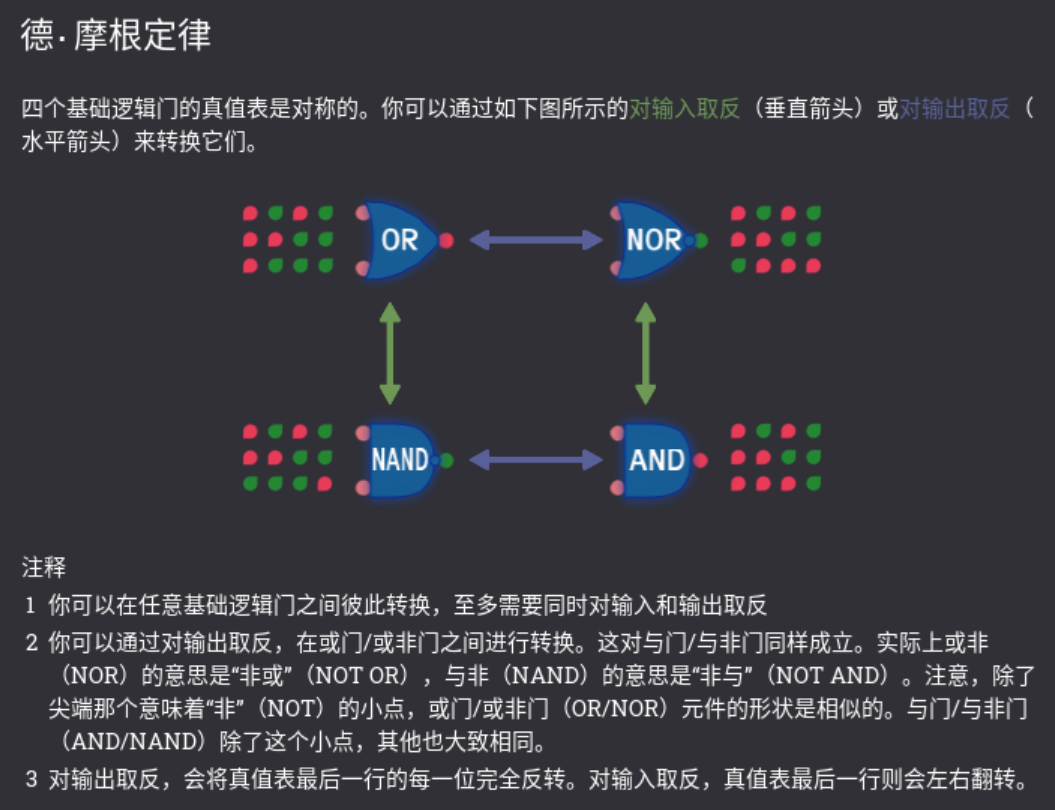
2.6 德摩根定律

• 至此我们可以发现，通过给已有的门原件的输入或输出三个地方添加非门的方法，可以造成真值表的某些翻转变化，从而得到我们想要的结果，这就是德摩根定律

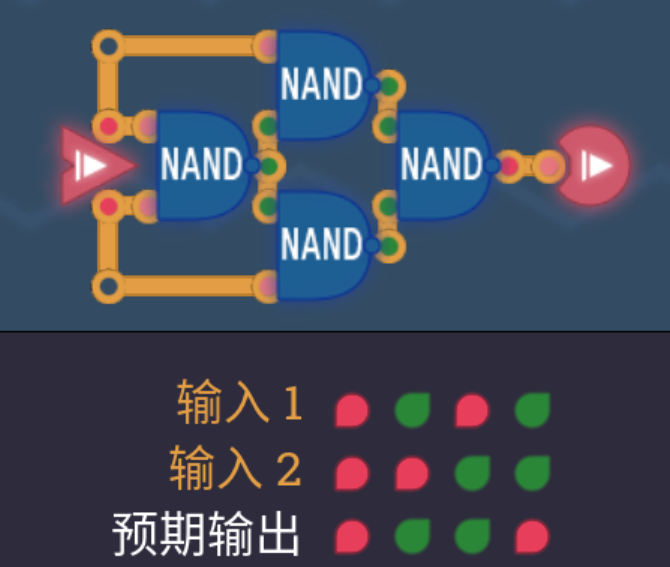
2.7 异或门XOR

• 我最开始想到的解法是这样的

• 仅用NAND的解法

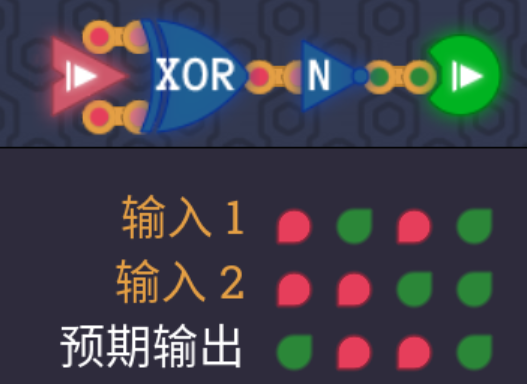
2.8 同或门XNOR

• 同或门可以通过对XOR的结果进行取反得来

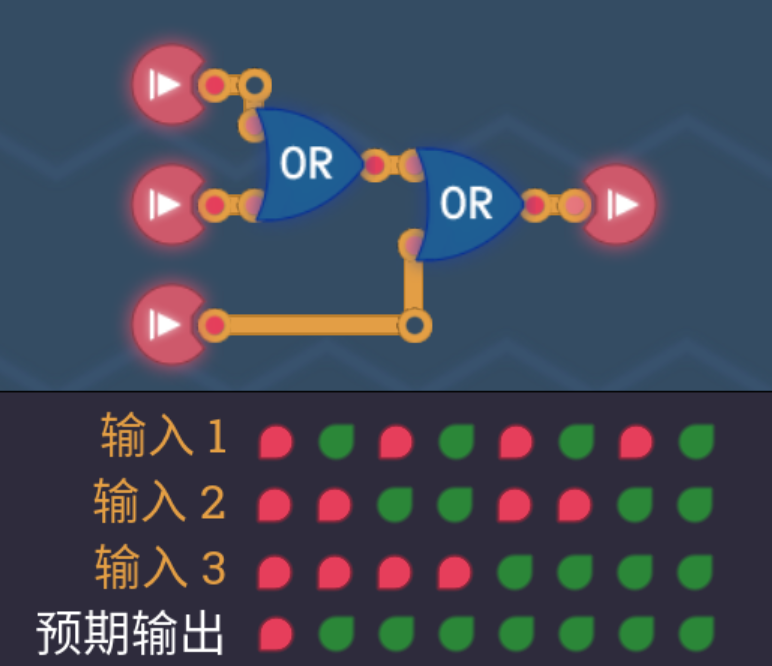
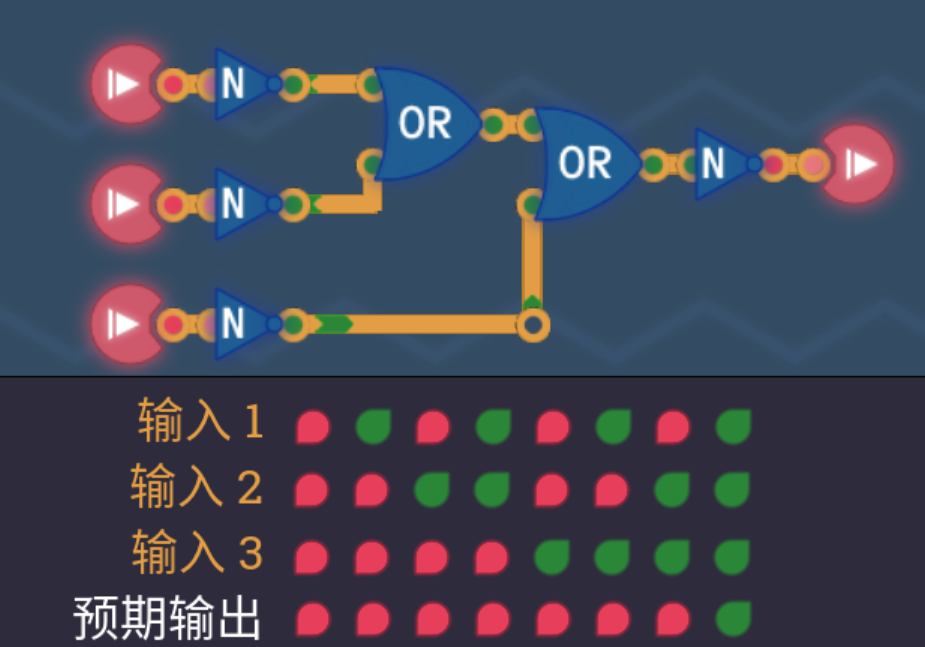
2.9 三路或门

• 对三路输入进行OR的逻辑运算

2.10 三路与门

• 对三路输入进行AND的逻辑运算

2.11 高电平

• 高电平就是无论如何都输出1信号的元器件，对其取反可以得到无论如何都输出0的元器件

三、第II章：算术运算与存储器

3.1 加法器

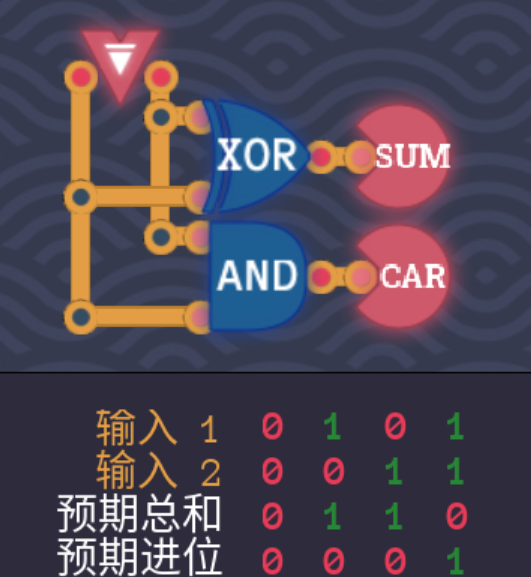
3.1.1 半加器与全加器

• 下图是一个半加器的实现，输入的两路数据是要进行相加的两个bit，输出一个相加的本位结果（SUM）和进位结果（CAR）

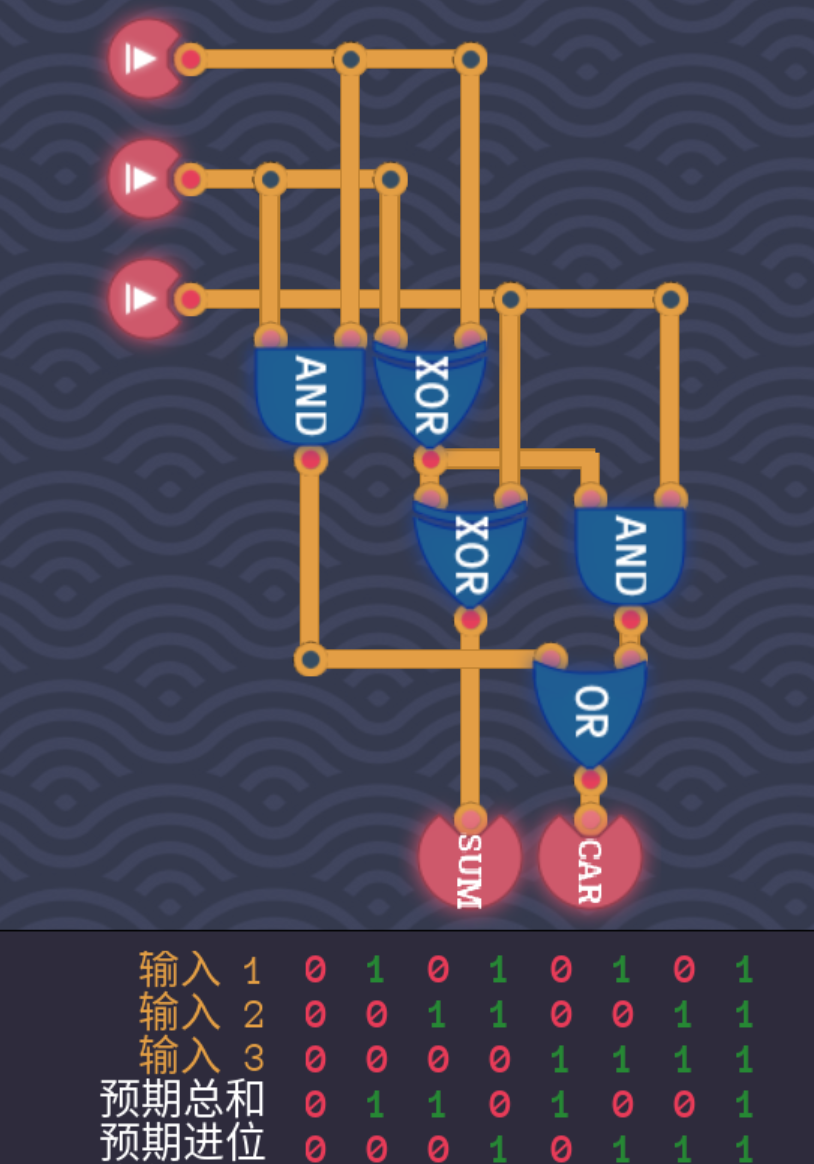
• 利用两个半加器和一个或门，就可以得到一个全加器，全加器就是接收前一位运算产生的进位结果纳入运算的1bit加法器

3.1.2 8bit加法器

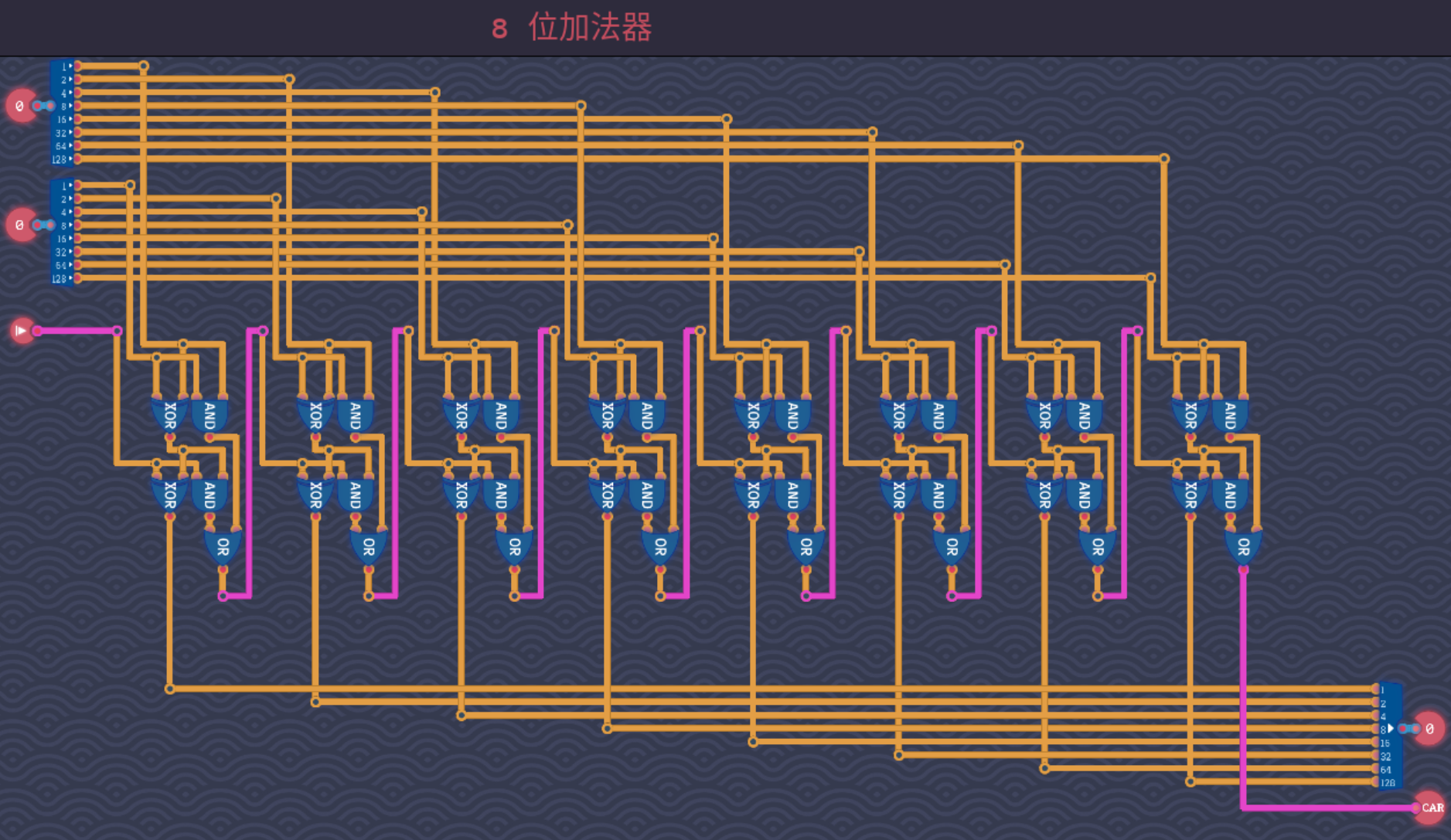
• 通过组合八个1bit的全加器，我们可以得到一个可以对两个一字节大小的二进制数进行加法运算的加法器，下面是8bit的超前进位加法器的实现

• 关于其原理，请参考我对应的博客：计算机中的整数及其四则运算相关笔记

3.2 多位逻辑运算

• 八位非运算的实现很简单，直接对各位取反即可

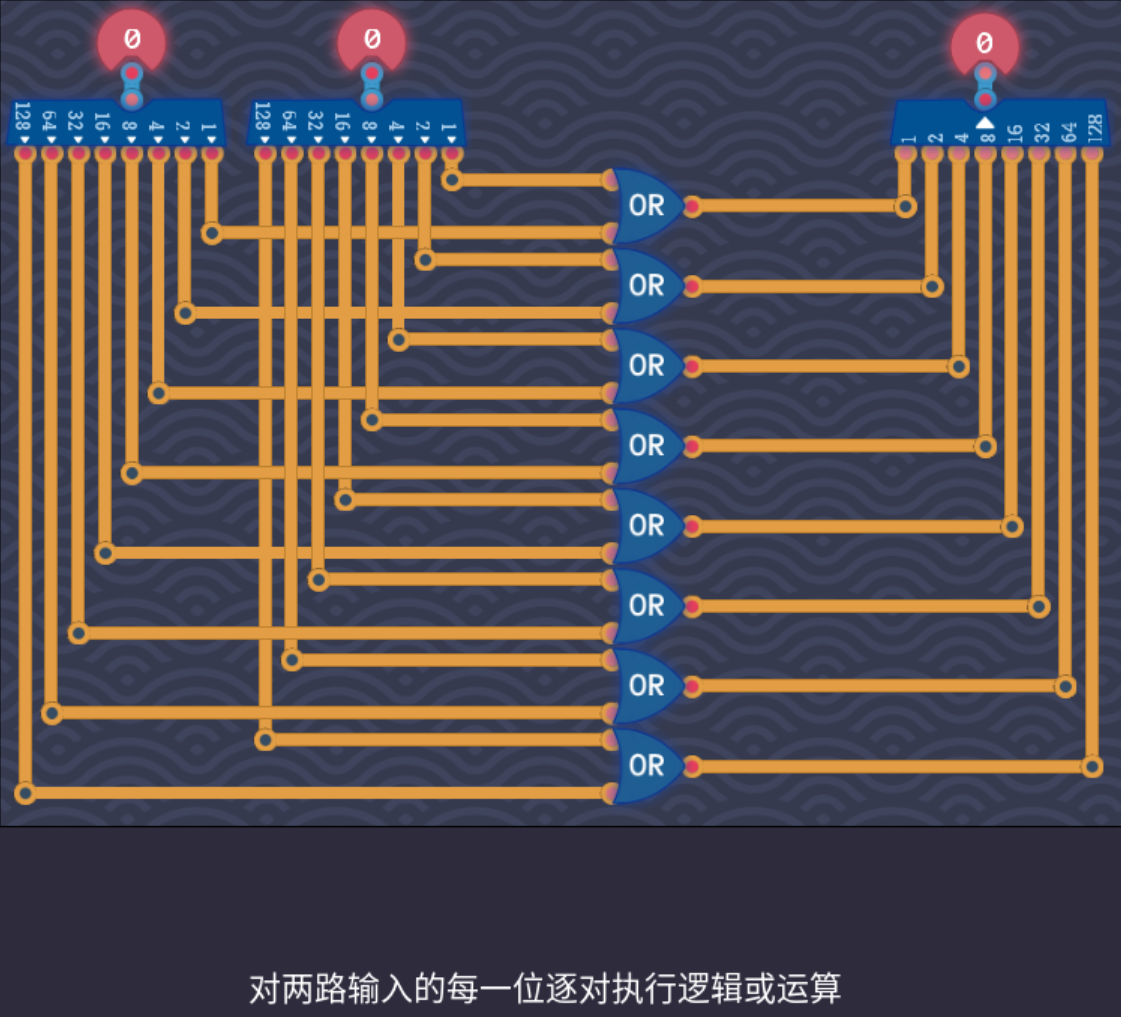
• 对于两个八位二进制数的或运算如下，其余逻辑运算同理

3.3 开关

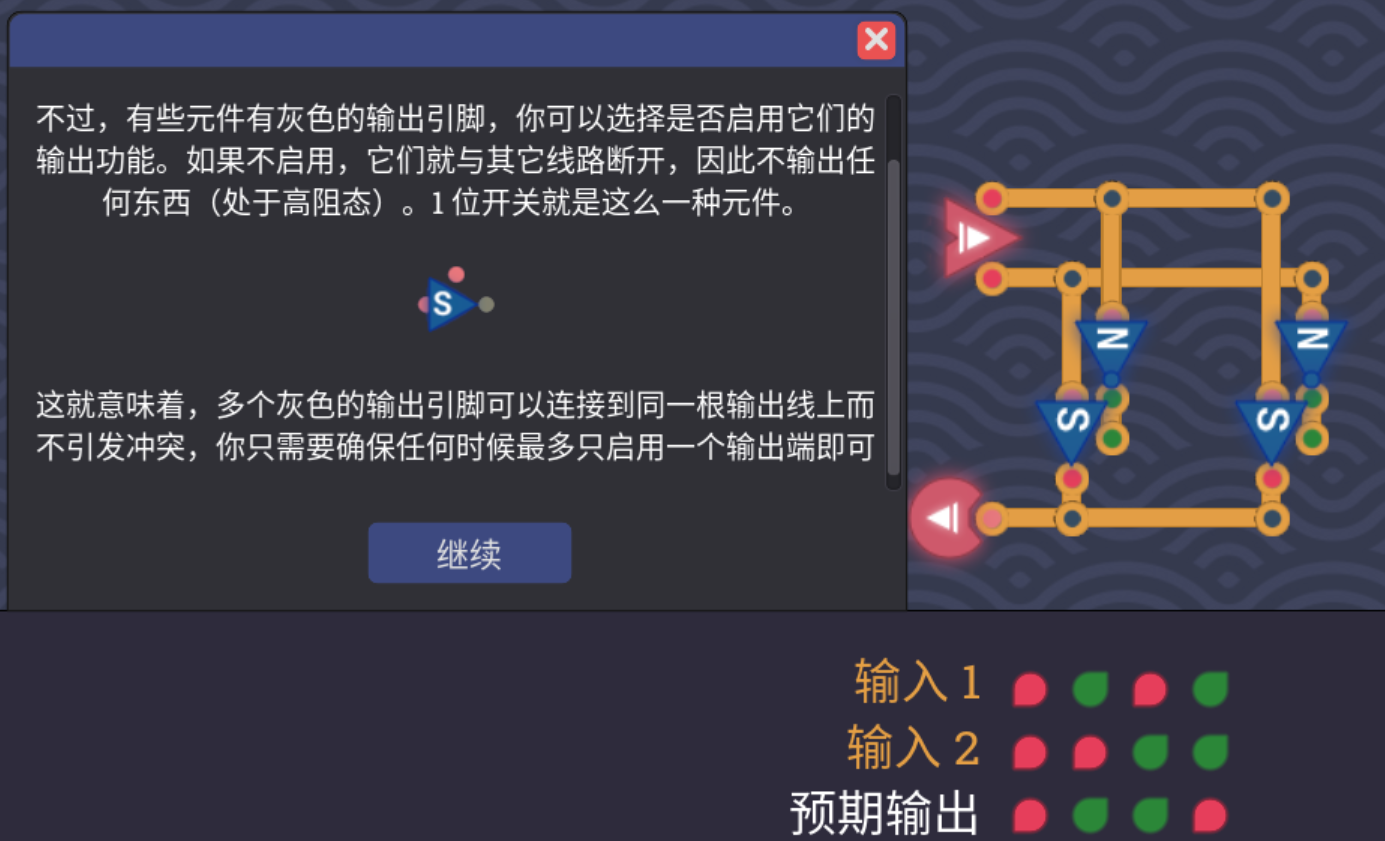
• 一位的开关的使用示例如下，我不知道是如何实现的，游戏直接给我们提供了1bit的和8bit的开关

3.4 数据选择器与总线

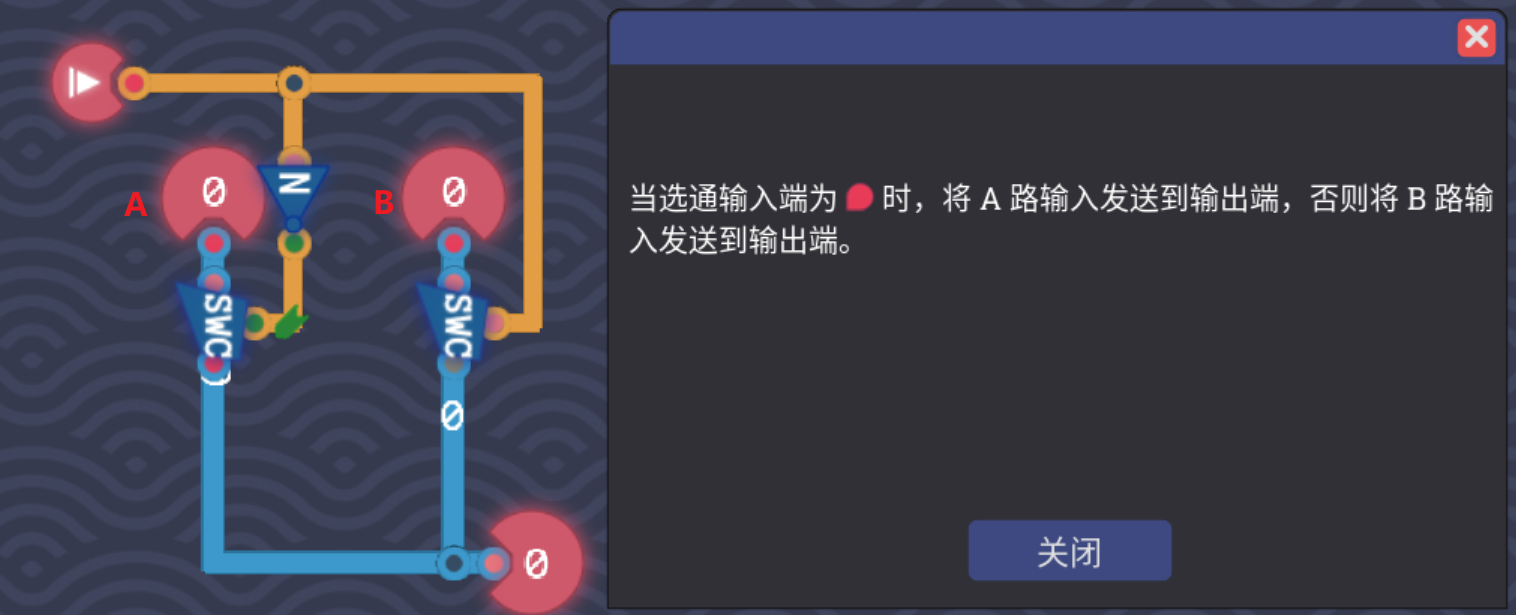
• 数据选择器可以帮助我们从多个数据中选择我们需要的那个，下面是一个2位的数据选择器

• 通过两个2位数据选择器，我们可以从两个数据输入源中选取一个，放到两个目的地中的指定一处，这就是总线

3.5 解码器

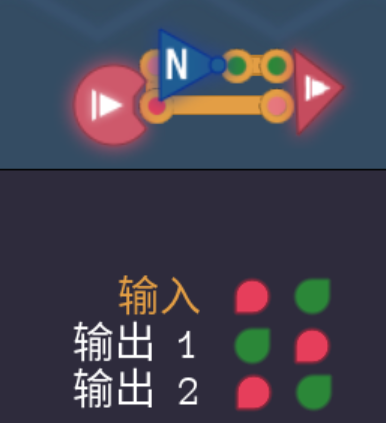
3.5.1 1bit解码器

• 1bit数据0或1可以表示$2^1=2$种不同的数，所以对于传入的1bit进行解码，我们可以映射到两种情况上去

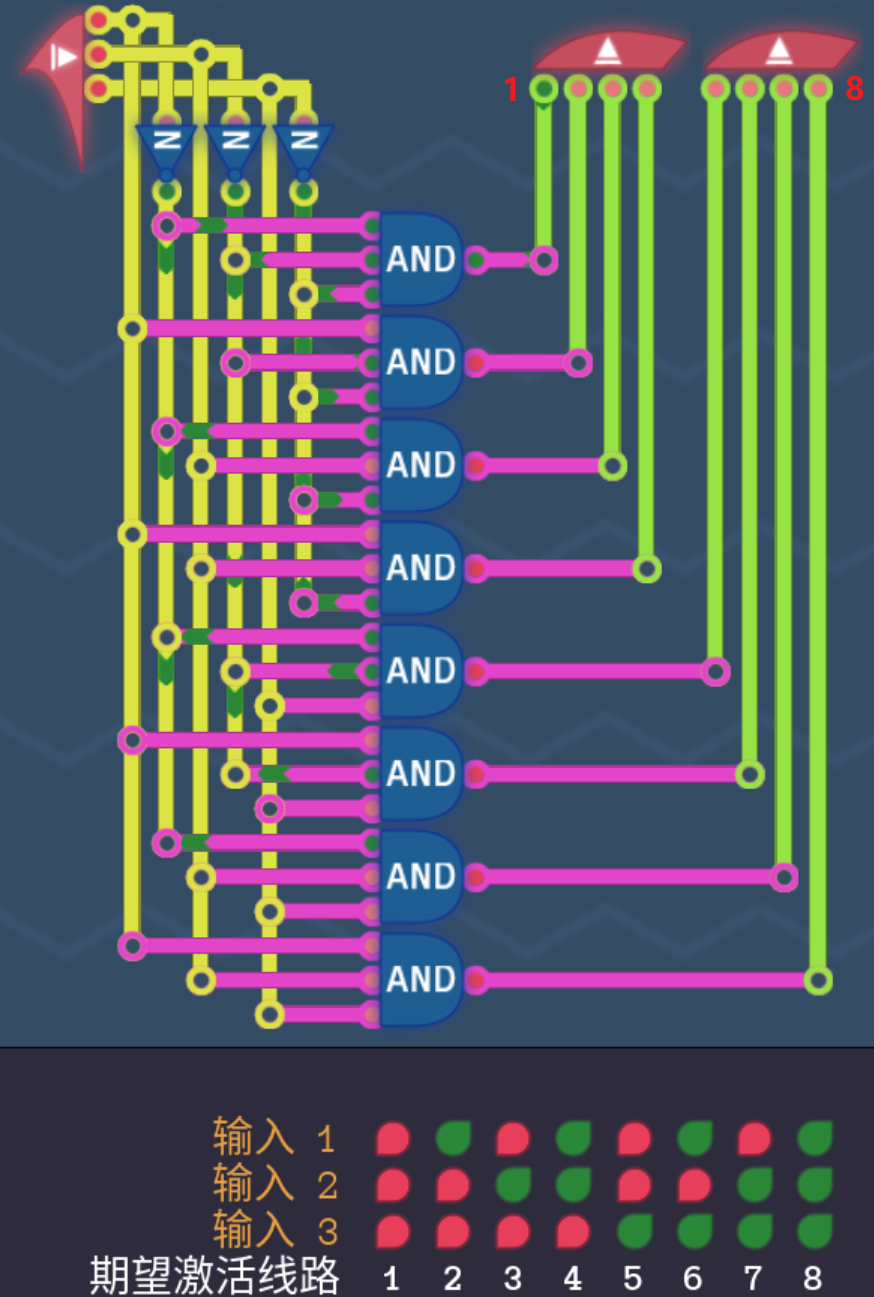
3.5.2 3bit解码器

• 3bit的数据有$2^3=8$种组合情况，所以可以对应八种不同的情况，我们可以通过对仅三位的输入进行解码，来指定八种不同的指令
• 下面是一个3bit的解码器的实现

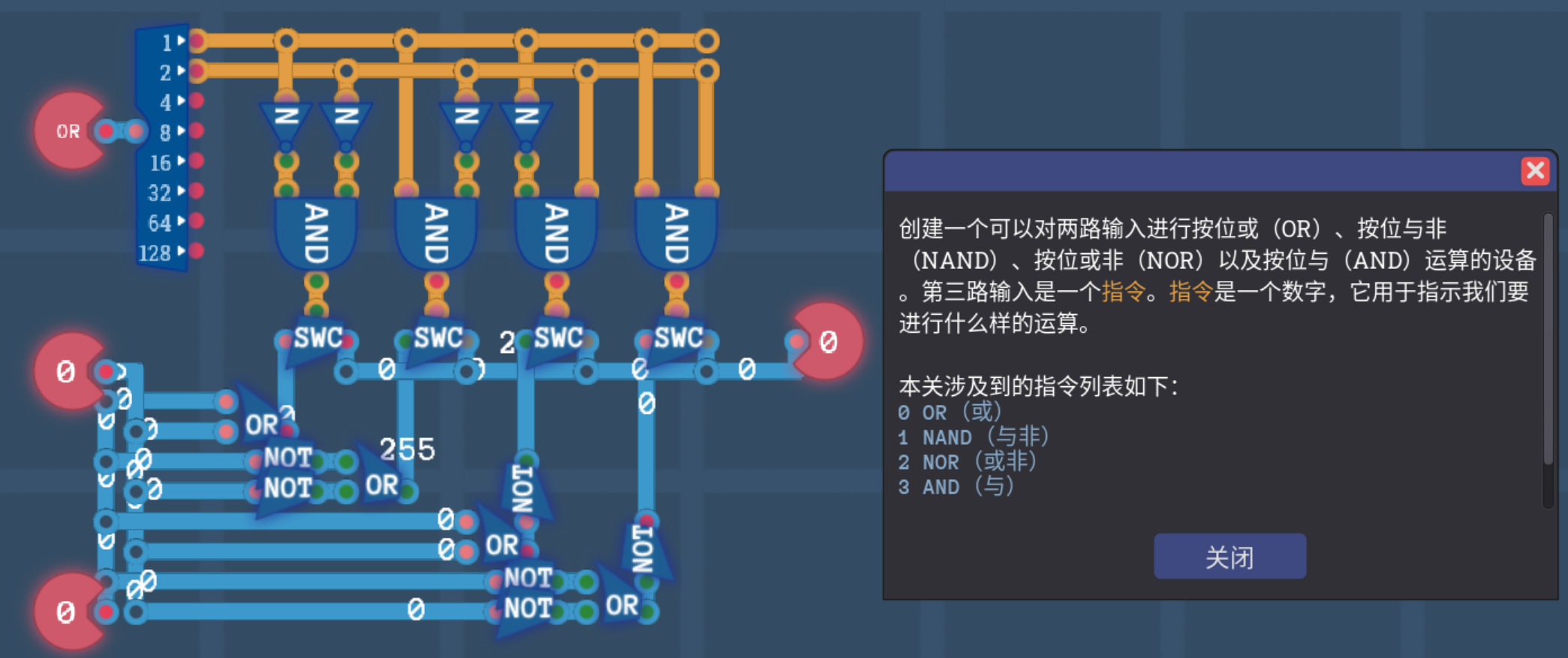
3.5.3 逻辑引擎

• 我们可以使用2bit的解码器来选取四种指令中的一个，将此指令用于传入的另外两个1bit的数据间的计算，并将结果输出

3.6 存储器

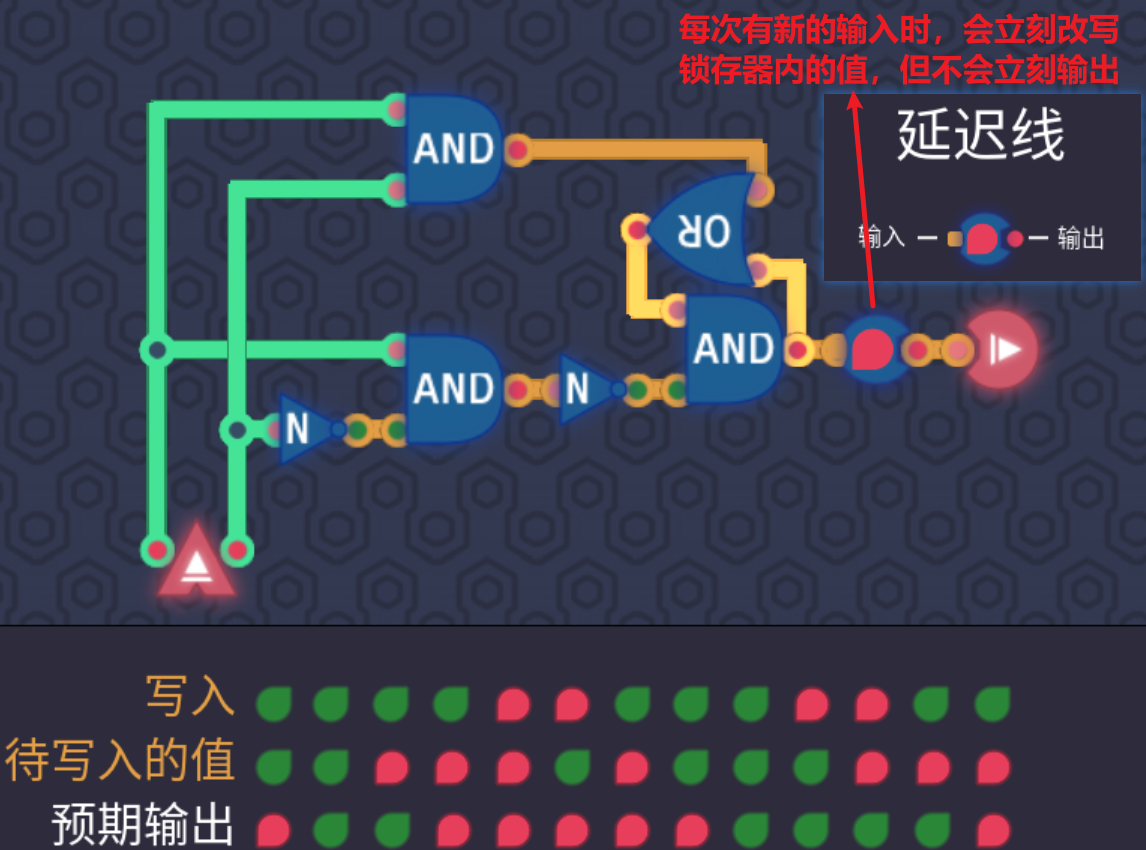
3.6.1 1bit锁存器

• 详细的原理参考我计组的存储器相关笔记（10.19当日暂未整理上传）

3.6.2 8bit寄存器

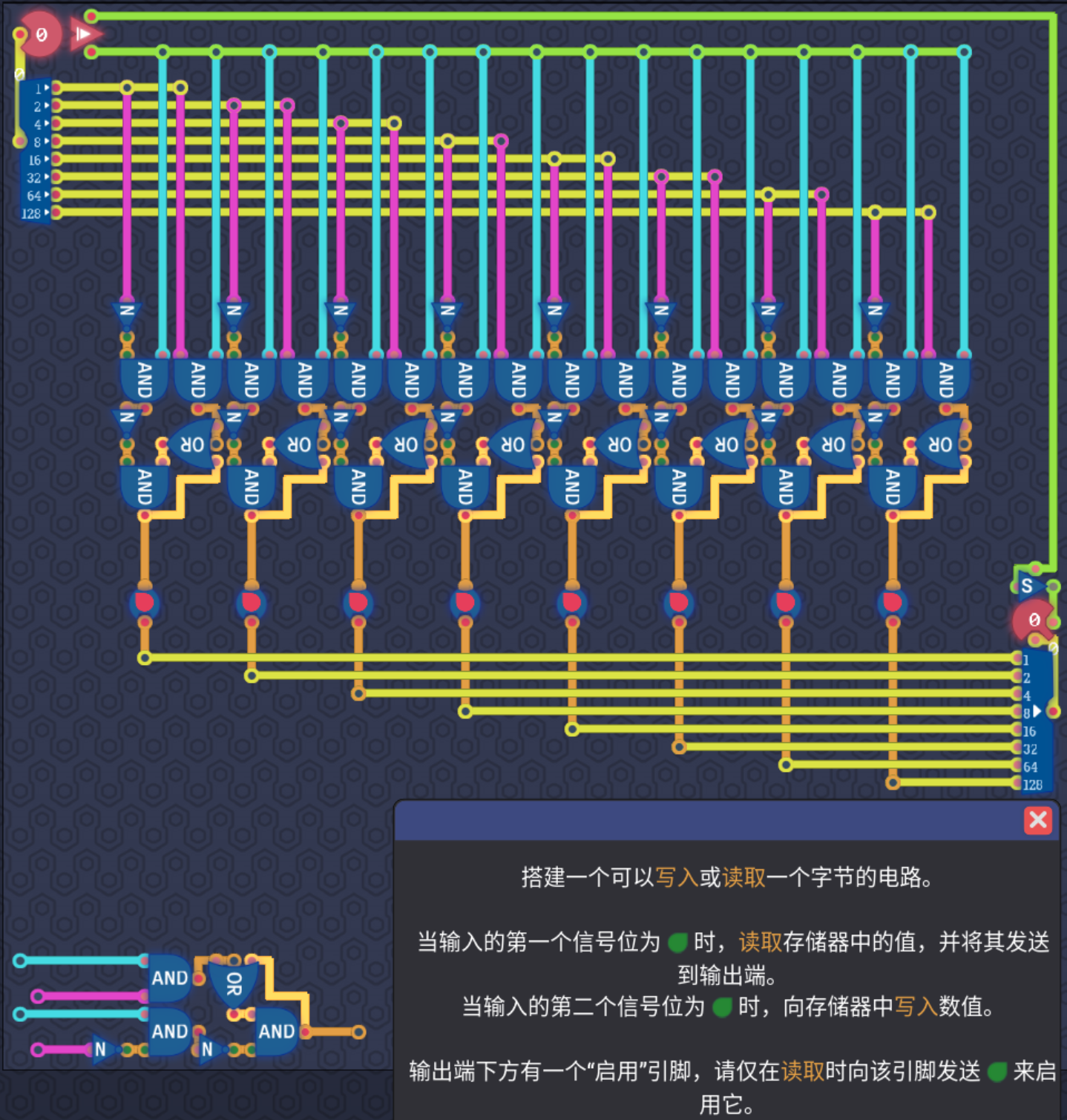
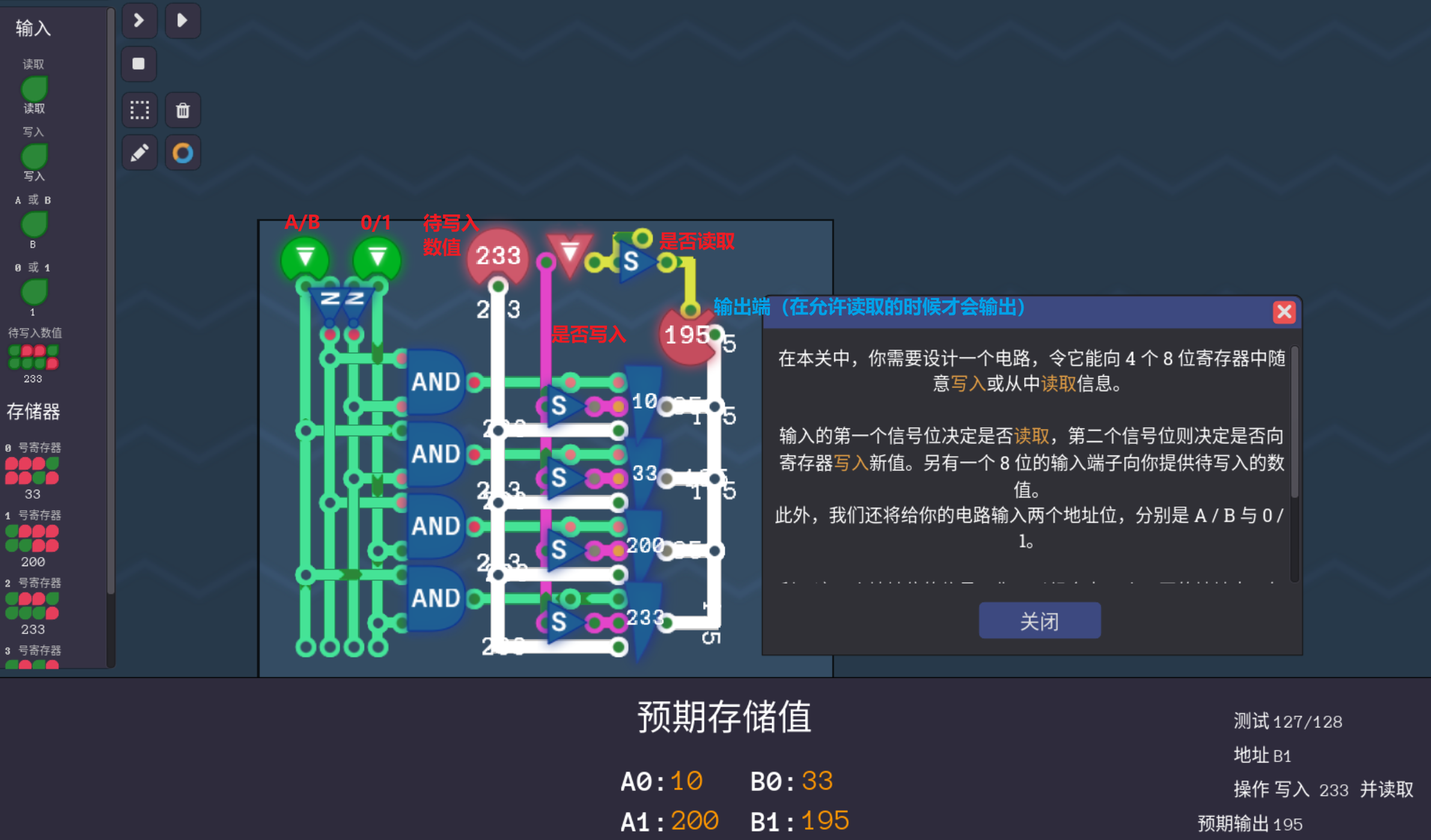
3.6.3 小盒子

• 我们结合8bit的寄存器以及2bit解码器，可以实现下面的需求功能，即对特定的寄存器进行擦写并决定其值是否要被输出，这其实已经有点接近处理器内的寄存器的管理方式了

四、第III章：处理器架构

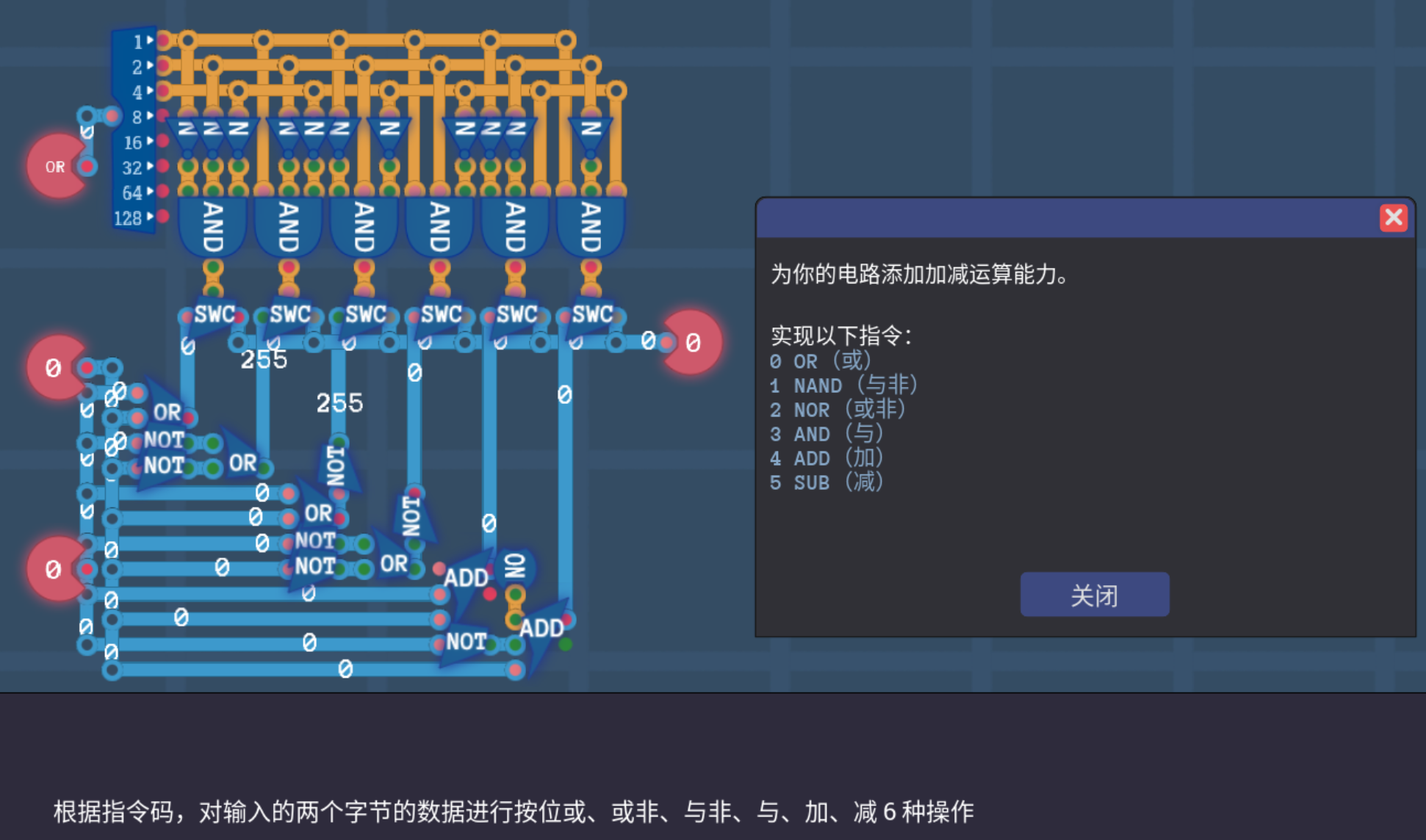
4.1 运算器ALU

• 我们对3bit数据进行解码，取用前6种情况用于对应6种指令（也就是说多出来两种未定义的指令）
• 下面的实现中，解码的部分搞复杂了，因为游戏直接提供了3bit的解码器原件，我忘记用了

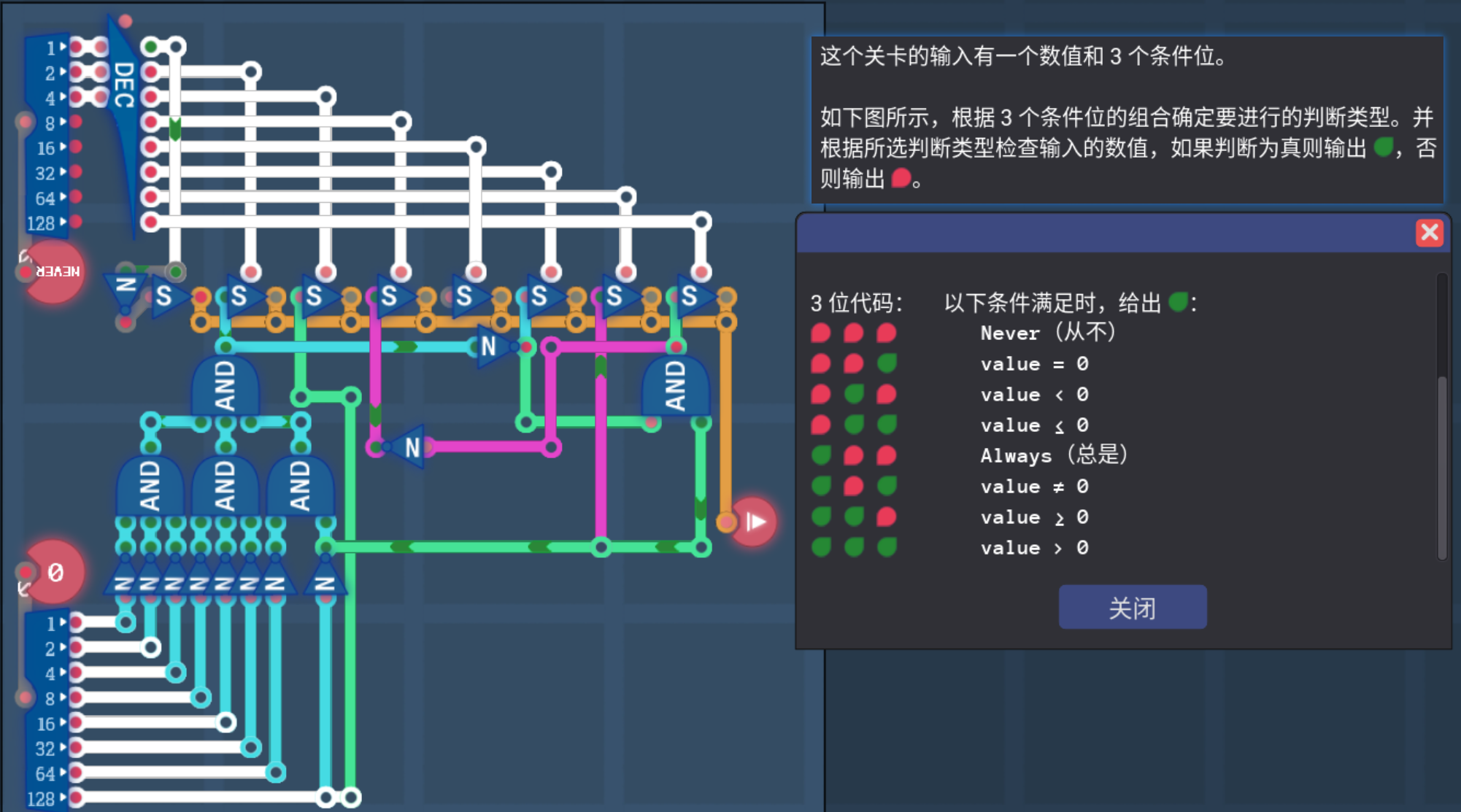
4.2 比较器COND

• 我们将传入的数据与0作比较（其实就是对传入的数据按位进行分析，比如首位符号位是1的话这个数就是负数），就得到了比较器

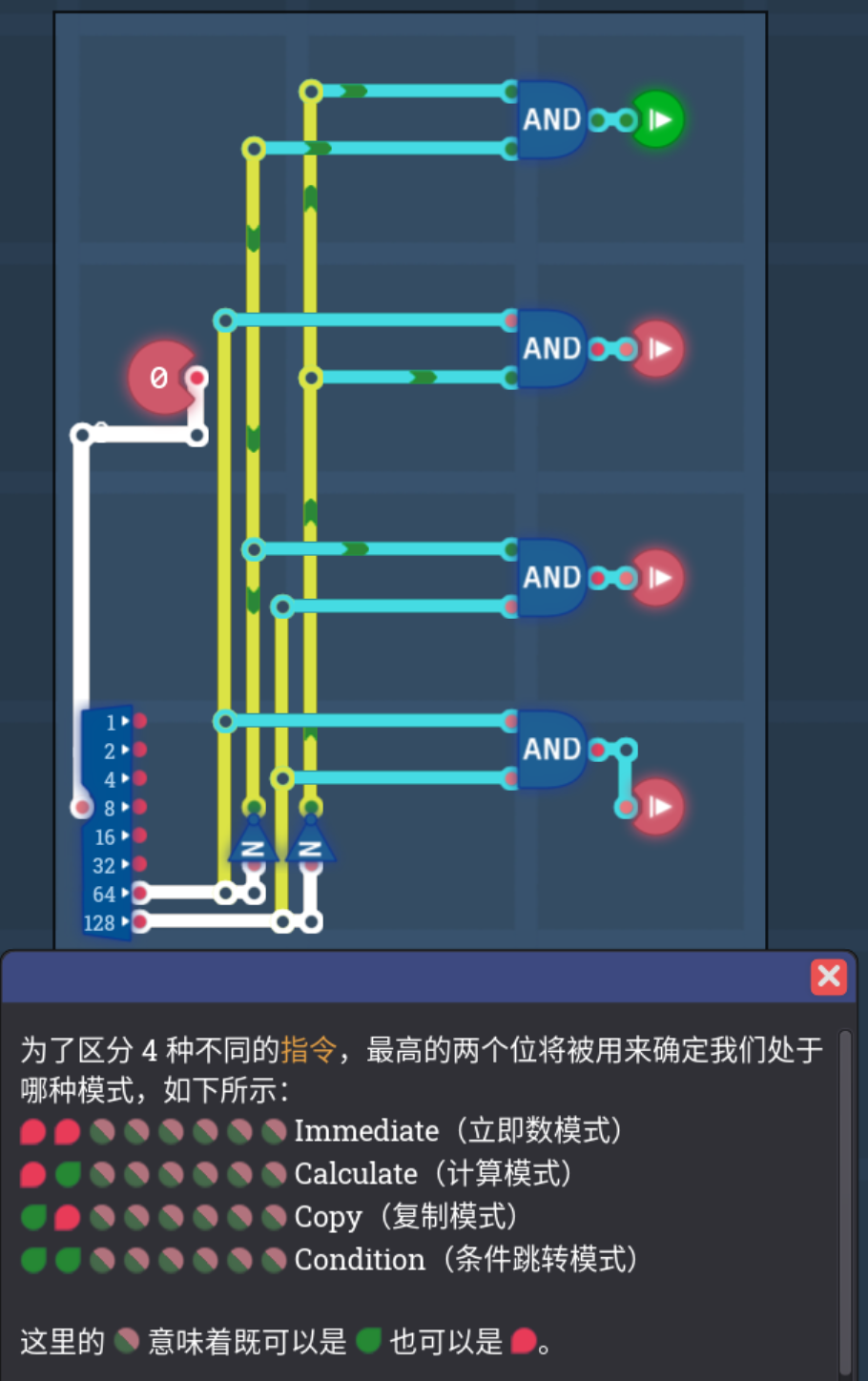
4.3 模式解码器

• 我们的处理器有四种模式，所以我们需要用2bit的数据进行解码，分别对应这四种模式

4.4 处理器四种模式

4.4.1 指令集

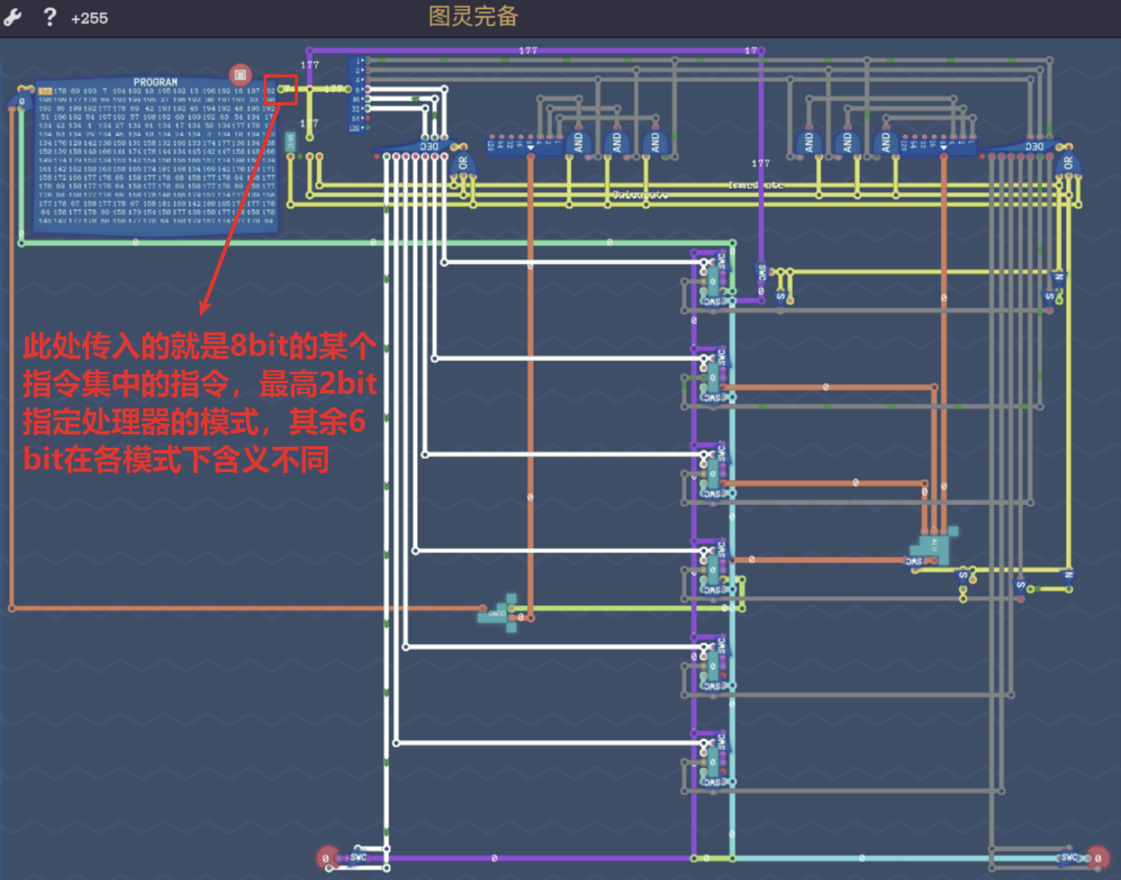
• 我们给处理器传入8bit数据，这就是指令，共有$2^8=256$种（其中有一部分指令是无意义的，因为某些模式下我们并没有将解码的每一种情况都用上），这些指令的集合称为指令集
• 指令集的最高2bit用于指定处理器的四种模式之一，下图是我实现的处理器架构

4.4.2 计数器

• 从8bit指令集中的256种指令中，任意选取若干需要的指令，将这些指令按顺序排布并存储，这就是程序
• 我们需要让程序中的指令按顺序执行，那么就需要每隔一段时刻就去从程序中取出下一个指令，作为输入传给处理器中进行处理，为此我们需要一个计数器

• 有了计数器后，我们就可以用计时器从0时刻开始自增，计数器的值就唯一对应程序中的某个指令，程序会在每个时刻将计数器的值对应的指令传入处理器，处理器就会根据传入指令进行下面四种模式之一的操作

• 注意计数器的值是可以可以被擦写的（条件模式就是为了擦写计数器），擦写后程序就会跳转到计时器此时的值对应的指令上

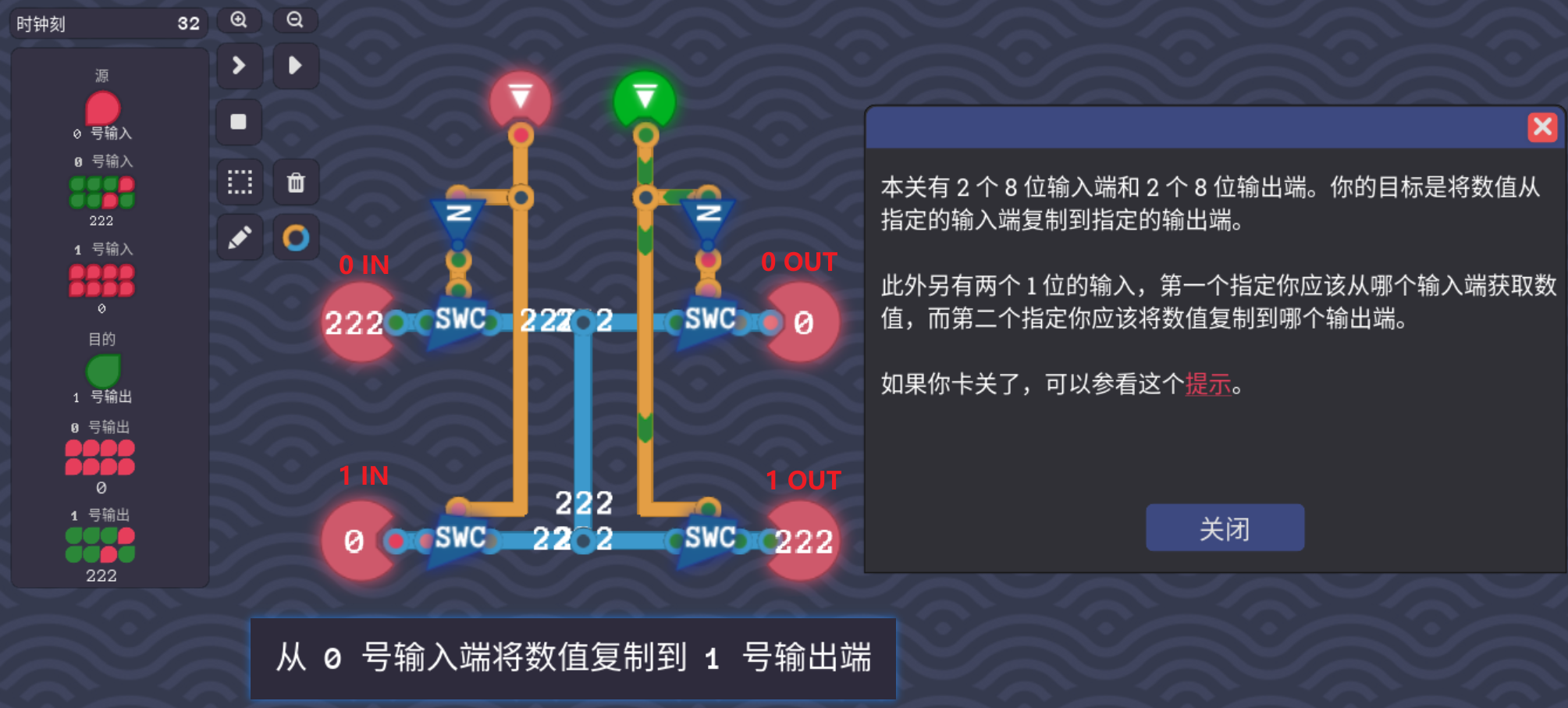
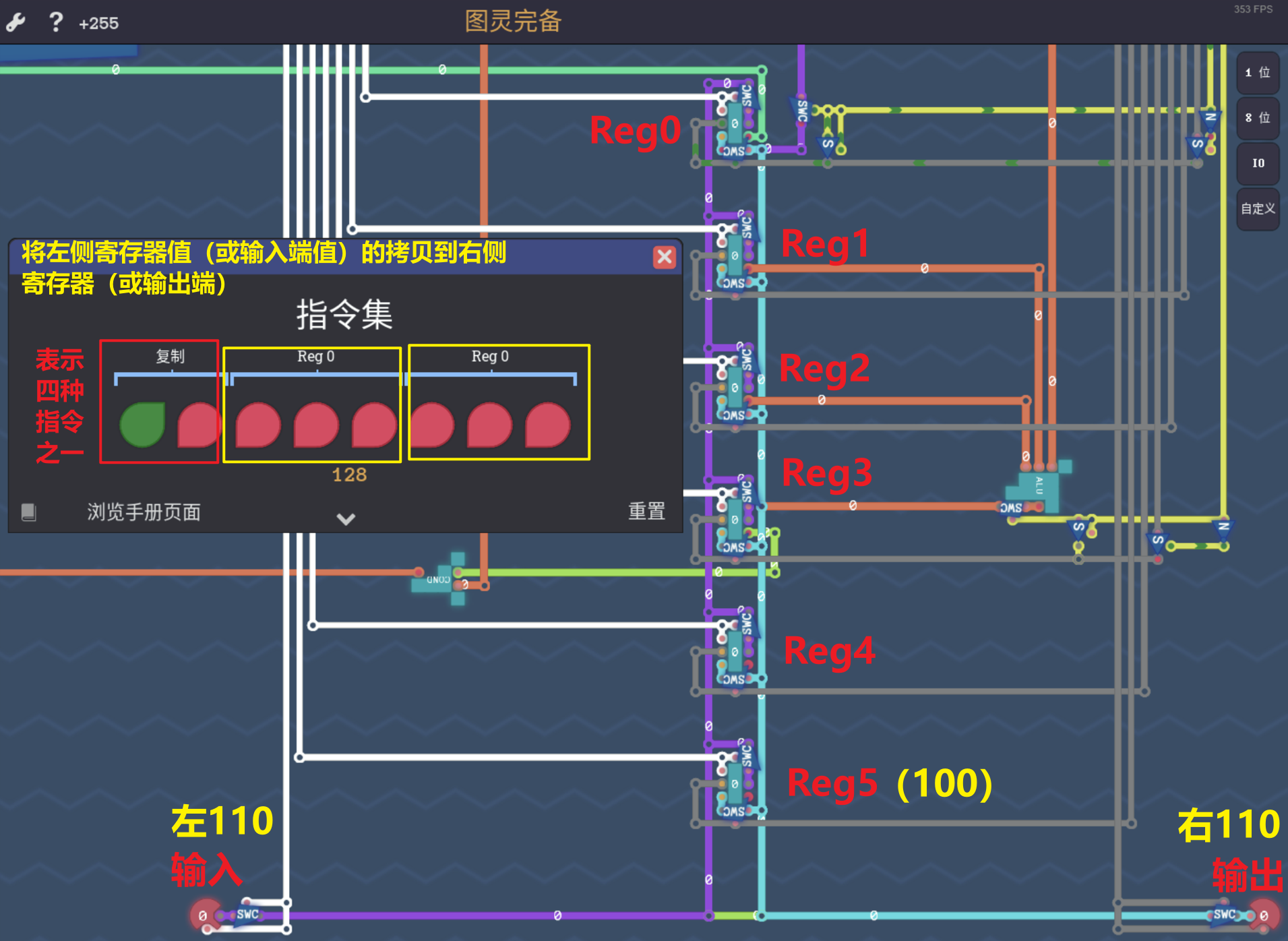
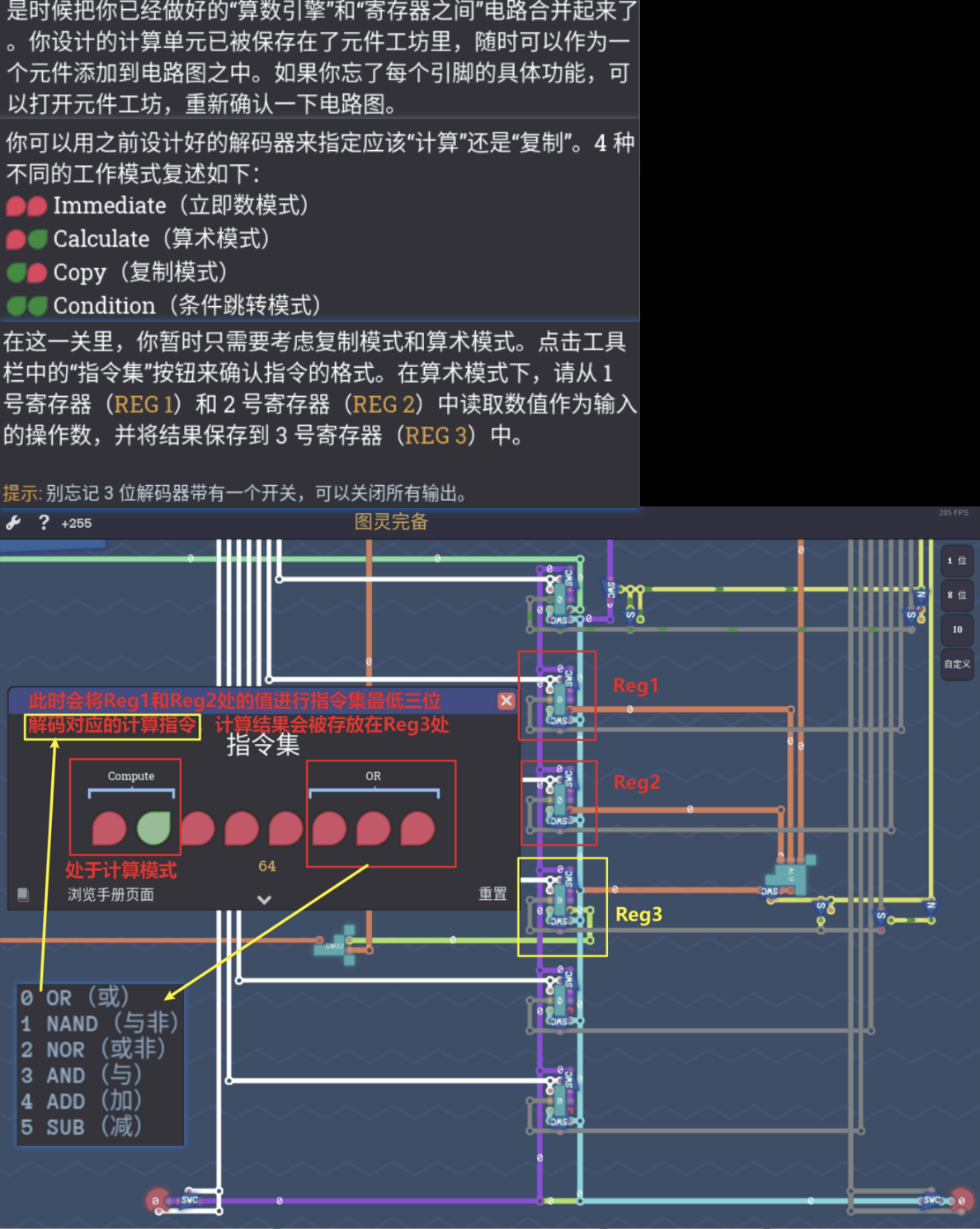
4.4.3 复制模式

• 如图所示，我注释写的很明白

4.4.4 计算模式

• 如图所示，该模式下会依据指令的最低3bit解码结果，借助ALU原件进行六种计算中的某一个，计算对象是1号寄存器和2号寄存器，计算结果存储在3号寄存器

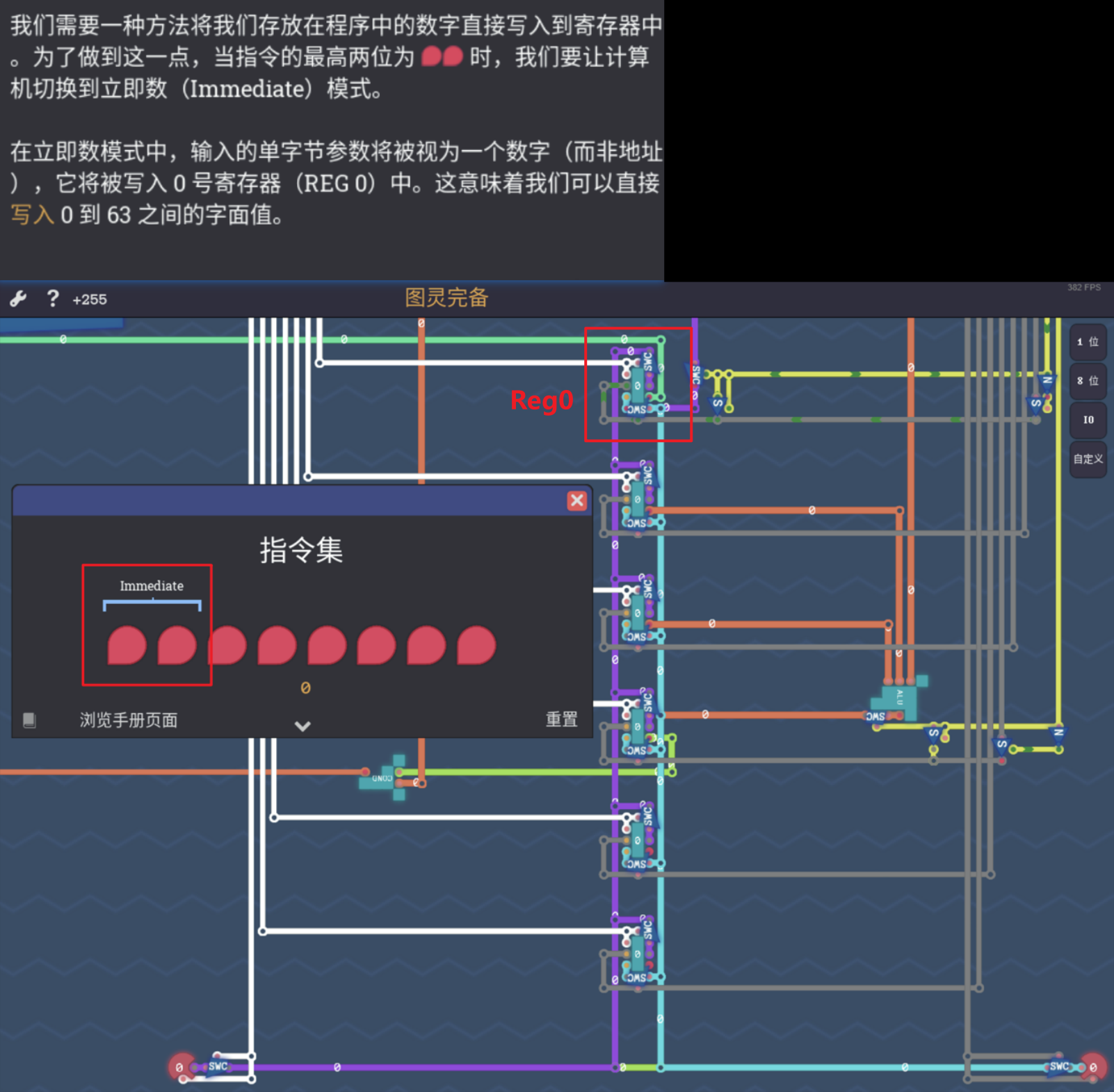
4.4.5 立即数模式

• 如图所示，该模式下会将传入的8bit指令的二进制数本身存入0号寄存器种

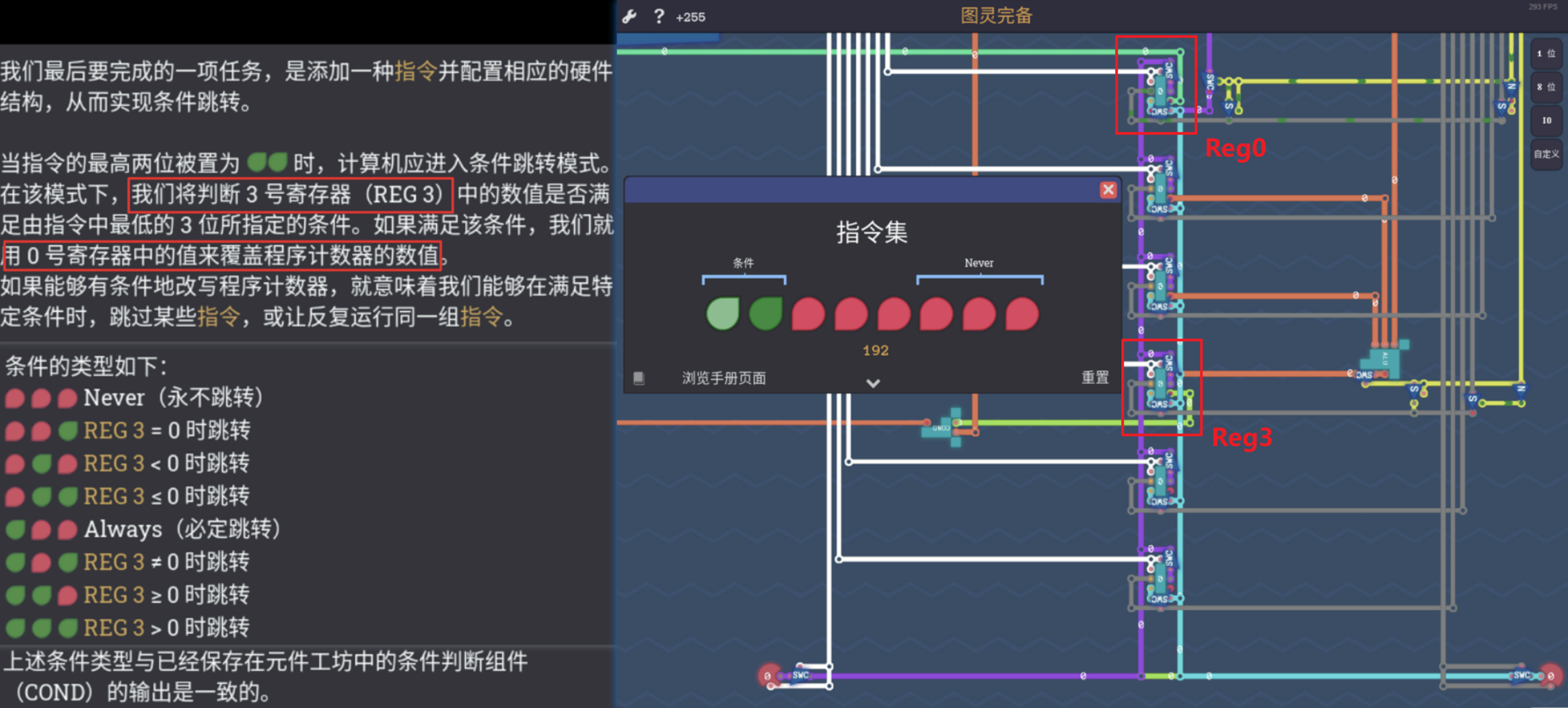
4.4.6 条件模式

• 如图所示，该模式下会将3号寄存器（即存放计算结果的寄存器，其内也不一定必须是计算结果，也可能是复制模式复制过去的某个值）内的数值根据指令的最低3bit对应的判断手段，借助COND原件进行比较
• 若COND传出1，则将0号寄存器内的值（即立即数模式传入的指令数，当然也可能是复制模式复制过去的某个数）用来擦写计数器

五、第IV章：汇编语言编程

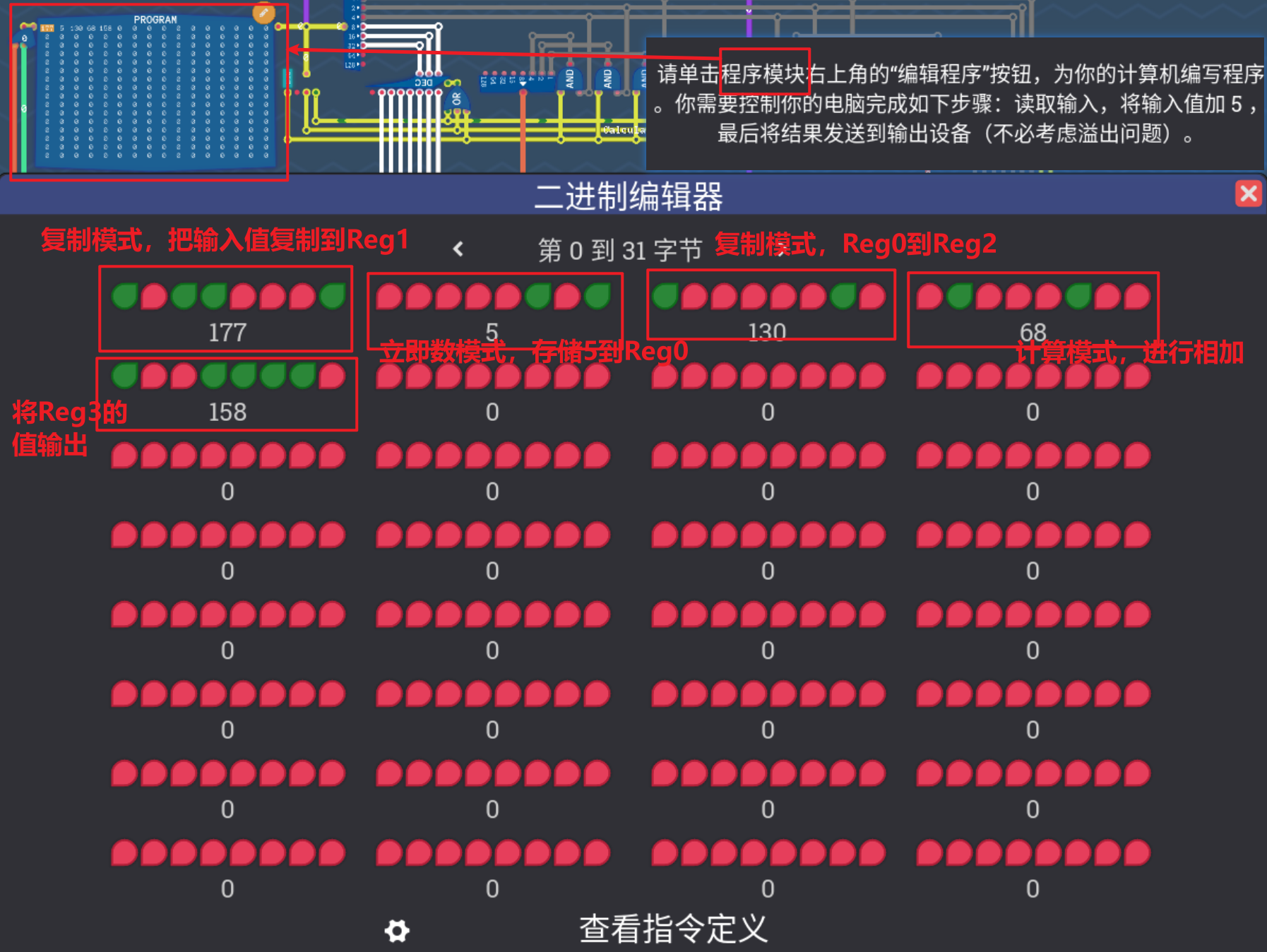
5.1 将输入值加五输出

• 直接设置若干个指令即可

5.2 根据传入半径计算周长

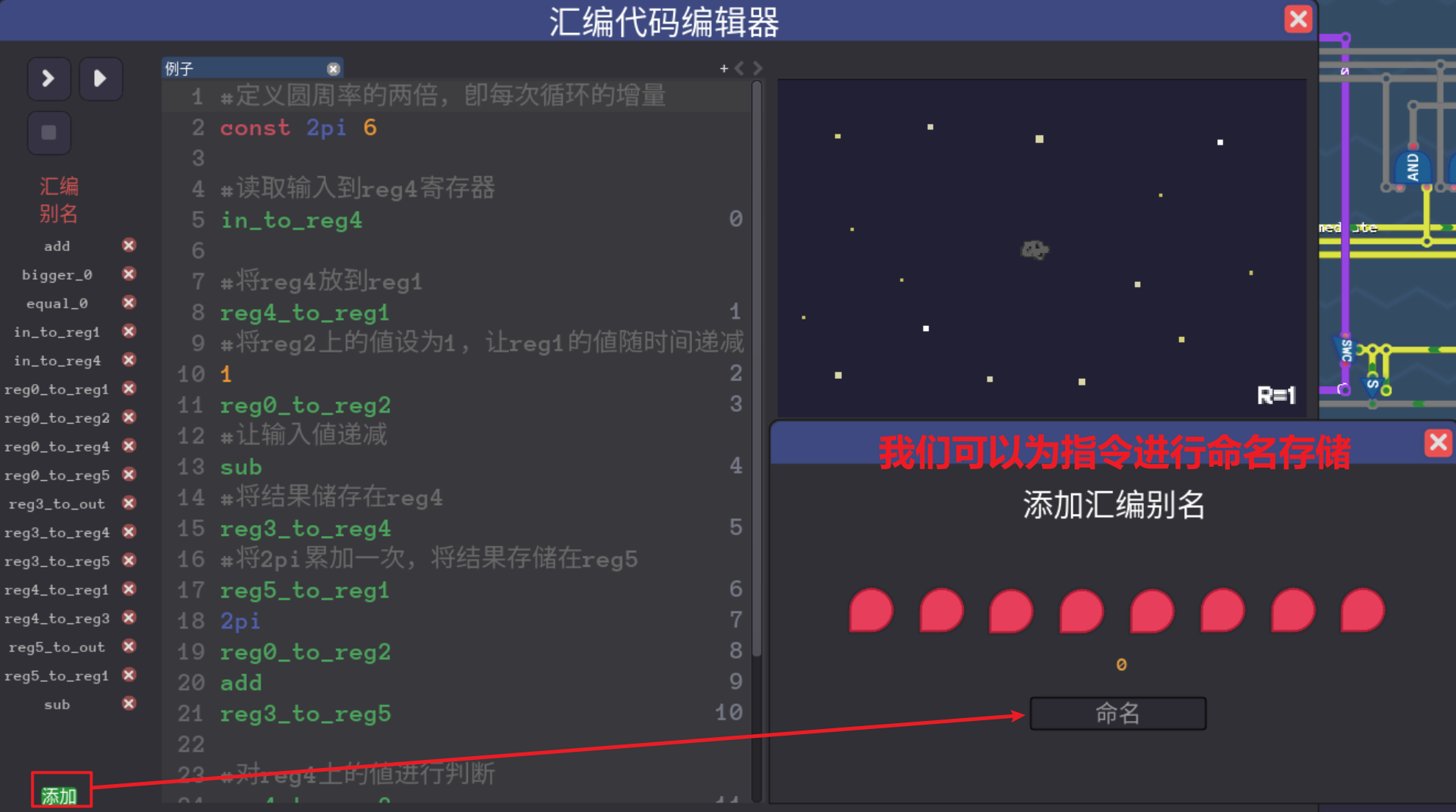
5.2.1 汇编语法与别名

• 汇编指令就是直接对寄存器进行操作

• 我们可以为特定的指令值设置别名，方便代码的编写与维护

5.2.2 汇编代码实现

• 我写的代码通过每次对传入的半径值进行递减1，每次递减对结果值进行判断，若是仍大于0就循环进行递减，在开始循环前要对结果值进行$2\pi$的递增，最终若将半径值消耗完了，就说明计算结束，可以将结果传出

#定义圆周率的两倍，即每次循环的增量
const 2pi 6

#读取输入到reg4寄存器
in_to_reg4

#将reg4放到reg1
reg4_to_reg1
#将reg2上的值设为1，让reg1的值随时间递减
1
reg0_to_reg2
#让输入值递减
sub
#将结果储存在reg4
reg3_to_reg4
#将2pi累加一次，将结果存储在reg5
reg5_to_reg1
2pi
reg0_to_reg2
add
reg3_to_reg5

#对reg4上的值进行判断
reg4_to_reg3
#若大于零，则返回循环开头处
1
bigger_0
#若小于等于则结束循环，将结果传出
reg5_to_out

• 你会发现我没有用运算符（因为我忘了可以用），其实在汇编代码中使用运算符的话，就会需要使用另一个处理器（或者ALU）对运算符两侧的8bit指令数进行运算，然后再将运算结果（8bit指令）输入当前处理器进行指令的执行，这就是电脑跑起来的原理（不断嵌套累加，算力就会递增）

六、写在后面

• 听说在第V章的”处理器架构II”的时候我们要对之前的所有实现进行重构，由于该游戏很难进行程序的调试，所以十分容易玩红温（害怕），有空再继续玩，哈哈

• 来自于一个月后的笔者留言：写这篇博客的时候我的”计算机组成原理”这门课才刚学到存储器，而现在已经基本学完了，在通关了这个游戏的这一部分之后，在后续学习计组这门课（ISA与处理器章节知识）的过程中每每学不懂时，我总能在从在这个游戏中实现的处理器中找到灵感：”这不就是游戏里的XXX嘛！”，快说谢谢游戏！我将后续学习的笔记贴在此处，以供能读到这里的读者参考

  • ISA中的指令格式设计与寻址模式
  • 处理器执行程序与指令的流程详解