关于DBS中的函数依赖与关系模式范式

一、函数依赖

1.1 函数依赖的定义

• 我们先考虑以下代数
  • $R$指代一个关系模式（即对排列格式相同的一类具体关系模型的抽象提炼）
  • $r$指代任意一个$R$的实例（即该抽象关系模式的一个具体关系模型实例）
  • $X$和$Y$分别是关系模式$R$中包含的属性（数据表$r$的列）的任意一种子集
  • $t_1$和$t_2$是关系模型$r$中的任意两个元组（数据表$r$的行）
• 若$t_1[X]=T_2[X]$可以推出$t_1[Y]=T_2[Y]$，则说明$X$和$Y$间具有某种联系，每一组这样的属性子集间的联系都称作$R$的一种函数依赖（Functional Dependency），此处记作$X\rightarrow Y$，注意该联系反向不一定成立

1.2 阿姆斯特朗公理

阿姆斯特朗公理（Armstrong Axioms）是用于推导函数依赖的一组基本推理规则，其中有三条最基本的规则，其余规则均可由这三者推导得出；关系模式$R$的属性集合为$U$，$X,Y,Z,W$等均为$U$的子集，用$F$指代$R(U)$的所有函数依赖的集合

1.2.1 基本规则

• 自反律（Reflectivity）：若属性子集$Y$是$X$的子集，则二者组成一对函数依赖$X\rightarrow Y$

\[Y\subseteq X\Rightarrow X\rightarrow Y\]

• 增广律（Augmentation）：对于已知的函数依赖$X\rightarrow Y$，其两边同时附加另一个属性子集形成的新函数依赖仍然成立

\[X\rightarrow Y\Rightarrow XZ\rightarrow YZ\]

• 传递律（Transitivity）：对于两组首尾相连的已知函数依赖，可递推得新的合法函数依赖

\[X\rightarrow Y\text{ and }Y\rightarrow Z\Rightarrow X\rightarrow Z\]

1.2.2 派生规则

• 合并律（Union）：对于单个属性子集$X$可推出的其它属性子集，$X$可推出这些子集取并集后的任意一个子集

\[X\rightarrow Y \text{ and }X\rightarrow Z\Rightarrow X\rightarrow YZ\]

• 分解律（Decomposition）：当$X$能推出$Y$时，也能推出$Y$的子集

\[X\rightarrow Y\text{ and }Z\subseteq Y\Rightarrow X\rightarrow Z\]

• 伪增广律（Pseudoaugmentation）：类似于自反律与增广律的合同产物

\[\begin{aligned} X\rightarrow Y&\text{ and }Z\subseteq W\Rightarrow XW\rightarrow YZ \\ (X\rightarrow Y&\text{ and }W\rightarrow Z) \end{aligned}\]

• 伪传递律（Pseudotransitivity）

\[\begin{aligned} X&\rightarrow Y\text{ and }WY\rightarrow Z\Rightarrow WX\rightarrow Z \\ (WX&\rightarrow WY\rightarrow Z) \end{aligned}\]

1.2.3 平凡函数依赖

• 对于函数依赖$X\rightarrow Y$
  • 若满足$Y\subseteq X$，则称$X\rightarrow Y$为平凡函数依赖（Trivial Functional Dependency），因为由于阿姆斯特朗公理中的自反律，$Y\subseteq X$是显而易见的
  • 若不满足，则称$X\rightarrow Y$为非平凡函数依赖（Non-Trivial Functional Dependency）

1.2.4 候选键严格定义

• 候选键是更严格的超键（关系中某个属性或属性组的值能唯一标识一个元组，则该属性或属性组称为超键），若关系中某个超键在去掉任一属性后不再成为超键，则其称为候选键
• 关系模式$R$的属性集合为$U$，$K$是$U$的一个子集，若$K$满足$K\rightarrow U$，且不存在一个$K’\subset K$能使得$K’\rightarrow U$，则$K$就是$R$的一个候选键

1.3 逻辑蕴含与两类闭包

1.3.1 逻辑蕴含的函数

• 若函数依赖集$F$中逻辑蕴含（Logical Implication）$X\rightarrow Y$，则根据$F$中的函数依赖，能够推导出函数依赖$X\rightarrow Y$，这记作

\[F\models X\rightarrow Y\]

1.3.2 函数依赖集的闭包

• 关系模式$R$的函数依赖集$F$的闭包$F+$指代包含$F$所逻辑蕴含的所有函数依赖的集合（离散数学中关系$R$的闭包$S$指的是在$R$的基础上新增几个元素组成新关系$S$，使得$S$是能够满足某种性质$P$的最小的关系，注意与此处的函数依赖闭包进行区分理解）

1.3.3 属性子集关于$F$的闭包

• 已知$X$是关系模式$R$的属性集$U$的一个子集且$F$是$R$的函数依赖集，那么属性子集$X$关于函数依赖集$F$的闭包记作$X+$或$X^+_F$，其指的是$F$所逻辑蕴含的所有$X\rightarrow A$（即$F$的闭包$F+$中所包含的所有$X\rightarrow A$）中的$A$的集合，注意$A$指的是单个属性而不是属性集

\[\begin{aligned} X^+_F&=\{A_i|A_i\in U,(X\rightarrow A_i)\in F+\} \\ \text{or } X^+_F&=\{A_i|A_i\in U, F\models(X\rightarrow A_i)\} \end{aligned}\]

• 注意函数依赖集$F$的闭包内的元素是函数依赖，而属性集$X$的闭包$X+$内的元素是单个属性而不是属性集，即使$X$本身可能是多属性集，例如下图示例中的$X,Y,Z$均为属性集，但答案中并不包含$X\cup Y$，${X,Y,Z}$的含义是将这三个属性集中的所有单个属性拆分存入集合

• 寻找$X+$的步骤具体如下
  • 第一步：初始化一个空集合$Q$，然后在其内存入$X$内的所有单个属性
  • 第二步：遍历$F$中所有$M\rightarrow N$的函数依赖，若$M\subseteq Q$则将属性集$N$拆分存入$Q$
  • 第三步：遍历完一轮后，若$Q$比遍历前更大，则重复第二步，直到不再变大

1.4 函数依赖集间的覆盖

• 给定某关系模式$R$的两个函数依赖集$F$和$G$
  • 若$F$能推导出$G$中的所有函数依赖，即$G$被$F$逻辑蕴含（$F\models G$），则称$F$覆盖$G$，$F$是$G$的一个覆盖（Covering），记作$G\subseteq F$
  • 若$F+=G+$（即$F\subseteq G+$且$G\subseteq F+$，即二者相互覆盖，能互相推导出彼此的所有依赖关系），则称$F$与$G$等价（Equivalent），记作$F\equiv G$

二、依赖集最小覆盖

目的是找到最简化的函数依赖集，这是规范化的要求之一

2.1 最小覆盖的定义

• 关系模式$R$函数依赖集$F$的最小覆盖（Minimal/Canonical Cover）是与$F$等价但形式最简的一个函数依赖集，记作$F_{min}$（其与$R$的任意函数依赖集间均是等价的），其满足以下性质
  • 无冗余函数依赖：$F_{min}$中所有函数依赖均必要，其之间不应当能够相互推导出
  • 右部仅一个属性：$F_{min}$中所有函数依赖$X\rightarrow A$的右侧$A$都是单个属性，而非属性集
  • 左部无冗余属性：$F_{min}$中所有函数依赖$X\rightarrow A$的左侧$X$可以是属性集，无冗余属性

2.2 最小覆盖的寻找

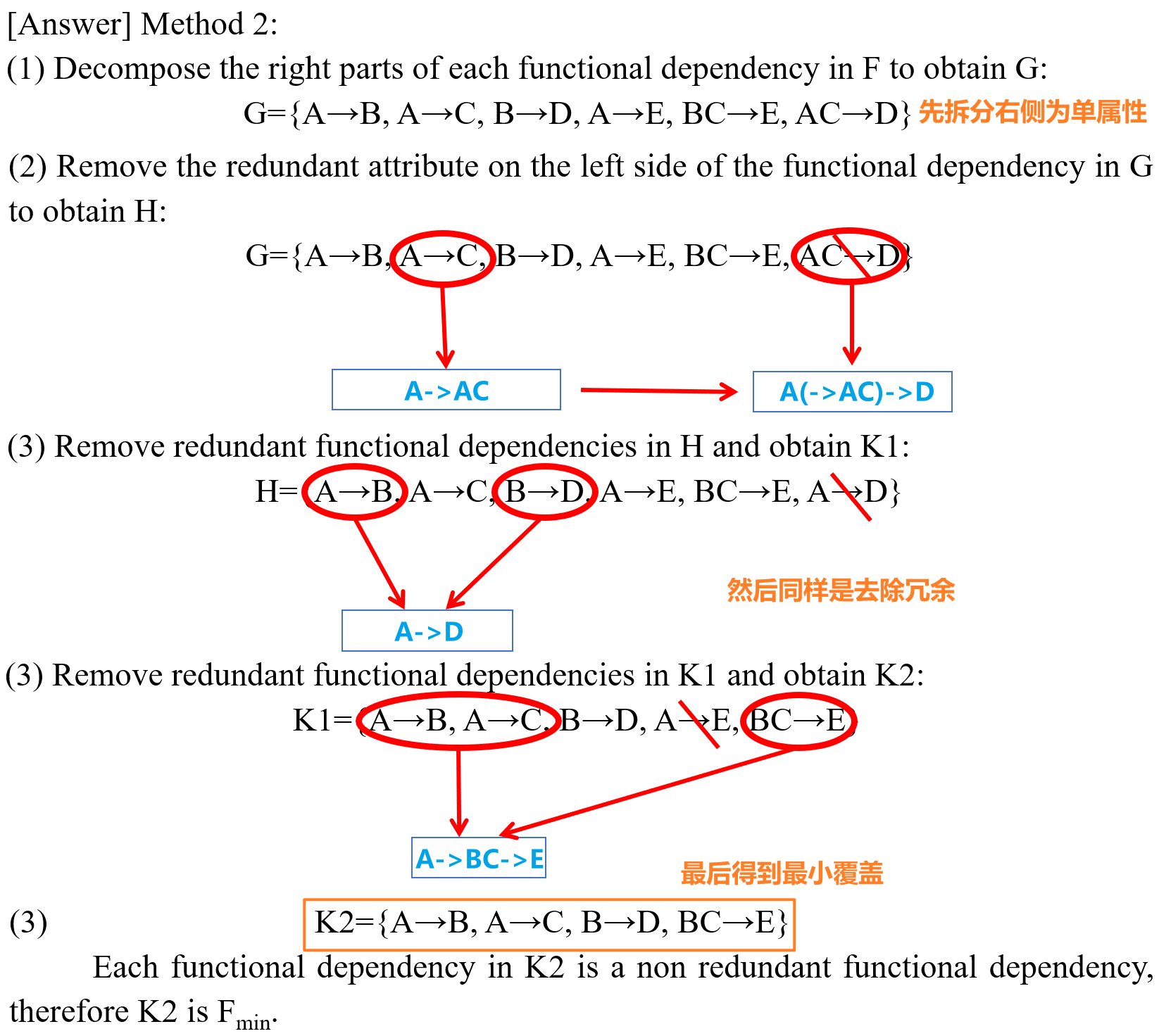
• 以下是通过两种不同的方式寻找某函数依赖集的最小覆盖的一道例题，最终答案相同

• 有时候对于同一个$F$通过不同思路得出的$F_{min}$可能不同，如下所示

三、关系模式的分解

目的是通过分解将关系模式简化，这是规范化的要求之一

3.1 分解的意义

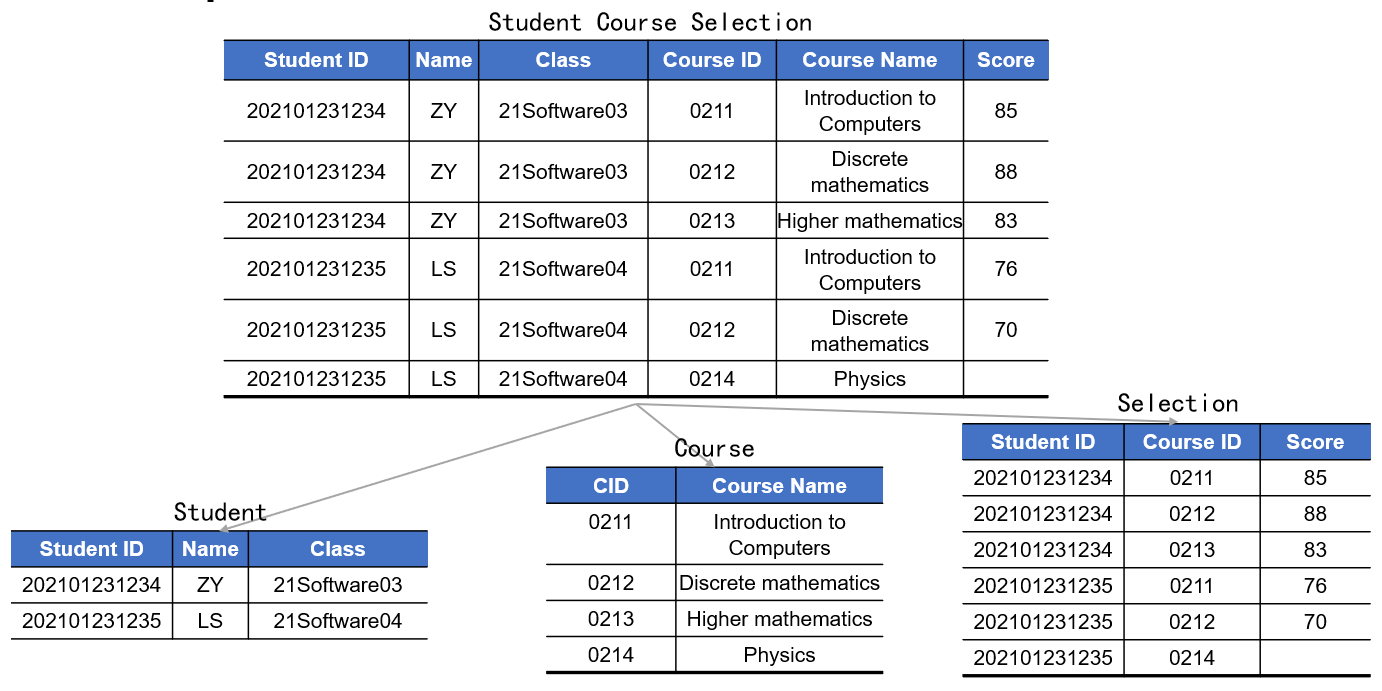
• 关系模式分解（Decomposition）即把一个大关系模式$R$拆分成多个小关系模式${R_1, …, R_n}$的方法，意在使得数据结构更清晰、减少数据冗余（Data Redundancy）和异常
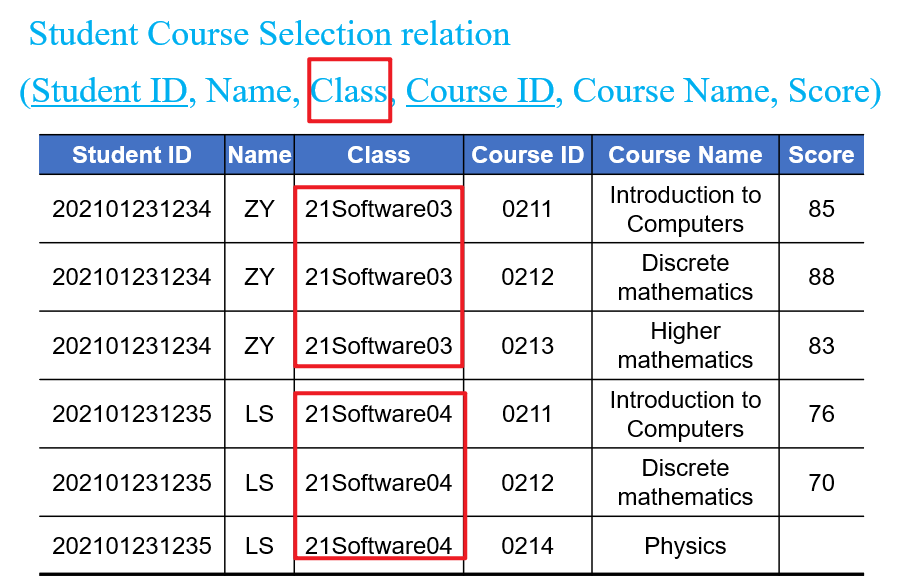
• 例如下图的大表中就存在数据冗余，导致修改某Student的Class字段时需在表中的多处连锁修改相同的数据，否则容易造成更新异常（Update Abnormaly）导致数据不一致，此时我们就可以使用关系模式分解将这单张大表拆分为多张小表，来减少上述重复劳动和风险

3.2 分解的原则

3.2.1 无损连接与保持依赖

• 关系模式分解应满足如下两个基本原则
  • 无损连接（Lossless Join）
    • 将分解后的关系模式自然连接（之前提过的关系代数）起来后必须能准确还原原始的关系
    • 这保证了分解前后的数据等价
  • 保持依赖（Functional Dependency Preservation）
    • 分解所得的子模式中的所有函数依赖必须完整体现原关系模式中的函数依赖
    • 这保证了分解前后的语义等价（Semantic Integrity）

3.2.1 遵循原则的分解案例

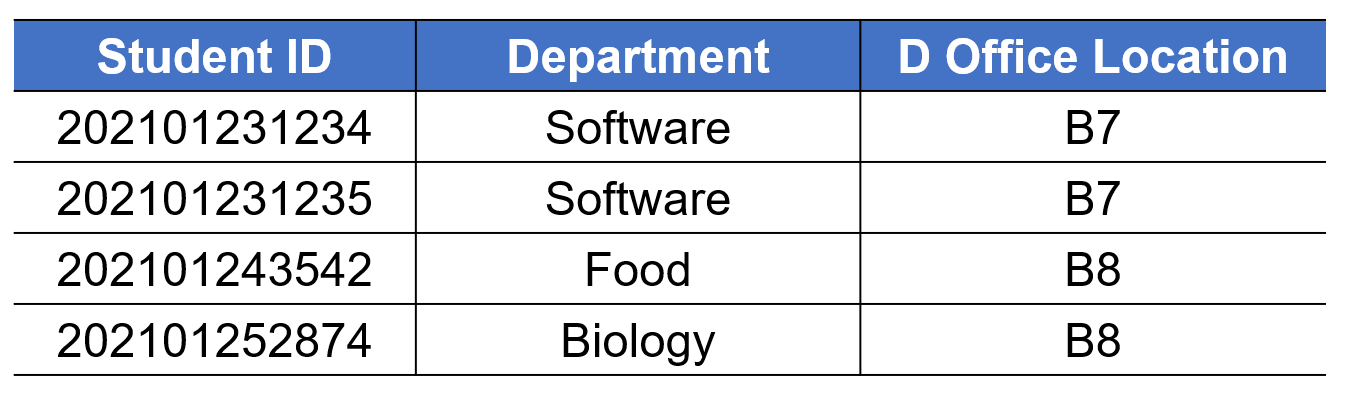
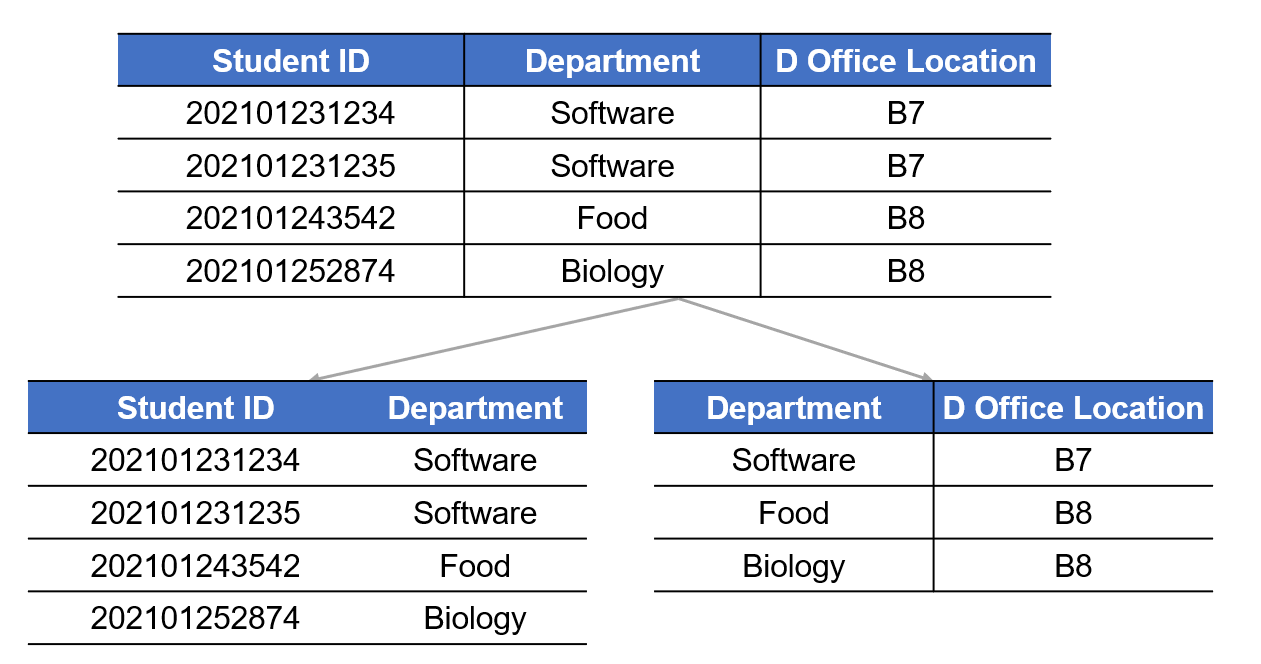
• 例如关系模式$R(StudentID,Department,DOfficeLocation)$的函数依赖集如下，下图是该关系模式的一个关系模型实例

\[F=\{Student\rightarrow Department,Department\rightarrow DOfficeLocation\}\]

• 将其分解为以下形式，即能保证自然连接后准确还原，也保有了原函数依赖

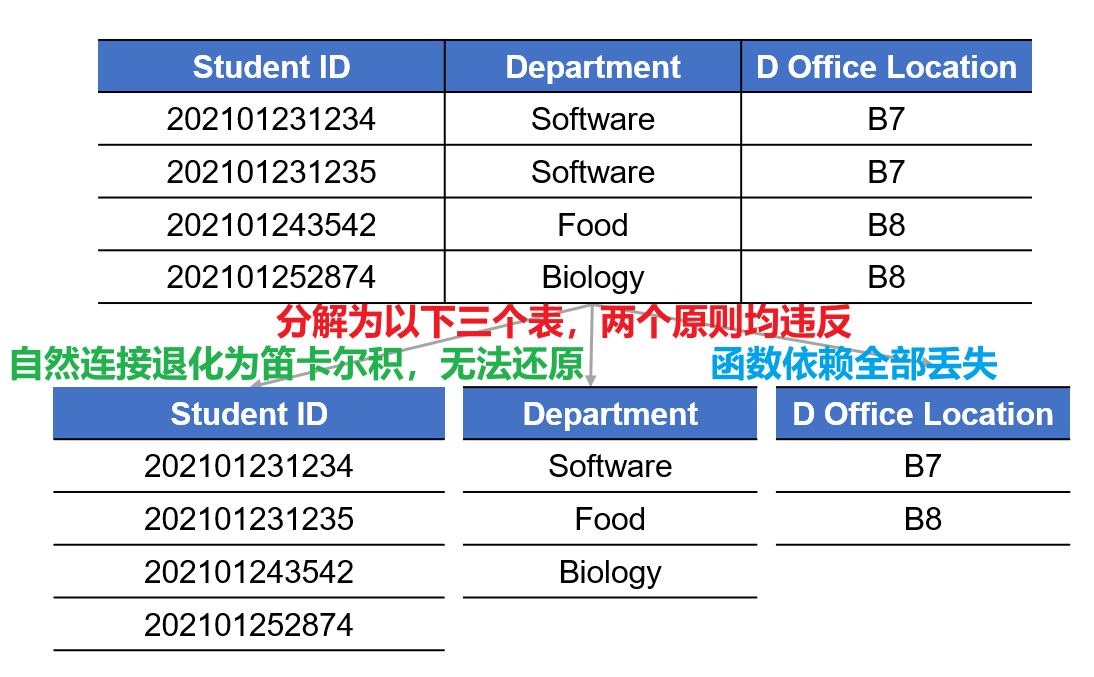
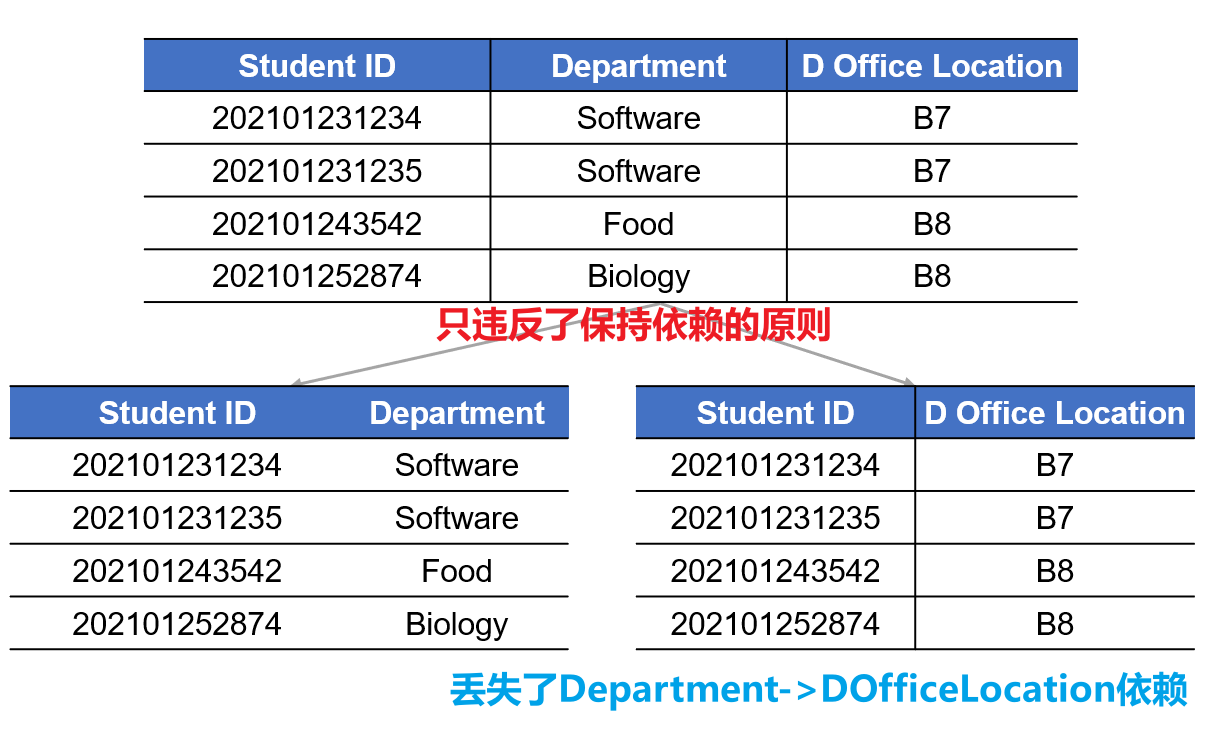
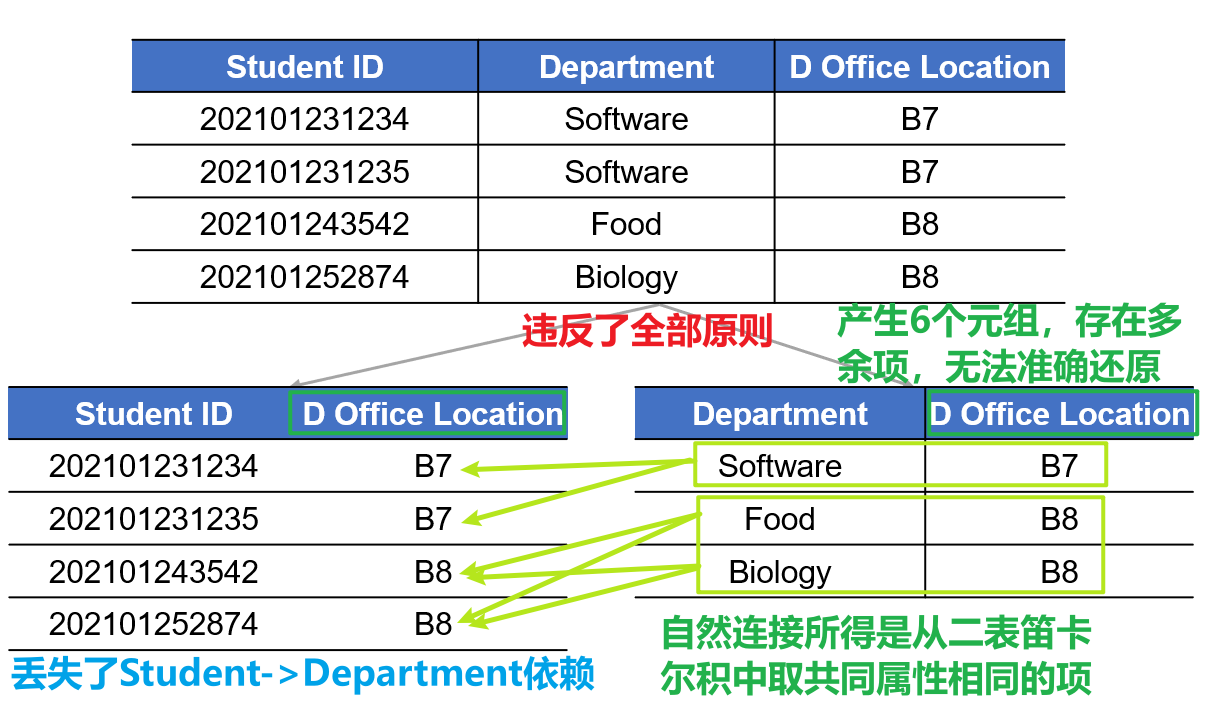
• 以下是几个反例，均违反了上述的两个原则之一或全部

3.3 确保无损分解

3.3.1 无损分解的定义

• 关系模式$R$被分解为$\rho={R_1,R_2,…,R_k}$，$F$是$R$的函数依赖集，如果$R$的任意一个关系模型实例$r$均能满足以下式子（即把分解所得的结果自然连接后，所得关系模式完全等同于分解前的关系模式），则该分解$\rho$被称为无损分解（Lossless Decomposition）

\[r=\pi_{R_1}(r)\Join\pi_{R_2}(r)...\Join\pi_{R_n}(r)\]

• 前文的无损连接原则相当于是要求所有分解都应当是无损分解

3.3.2 无损分解的判别

3.2.2.1 矩阵判别法

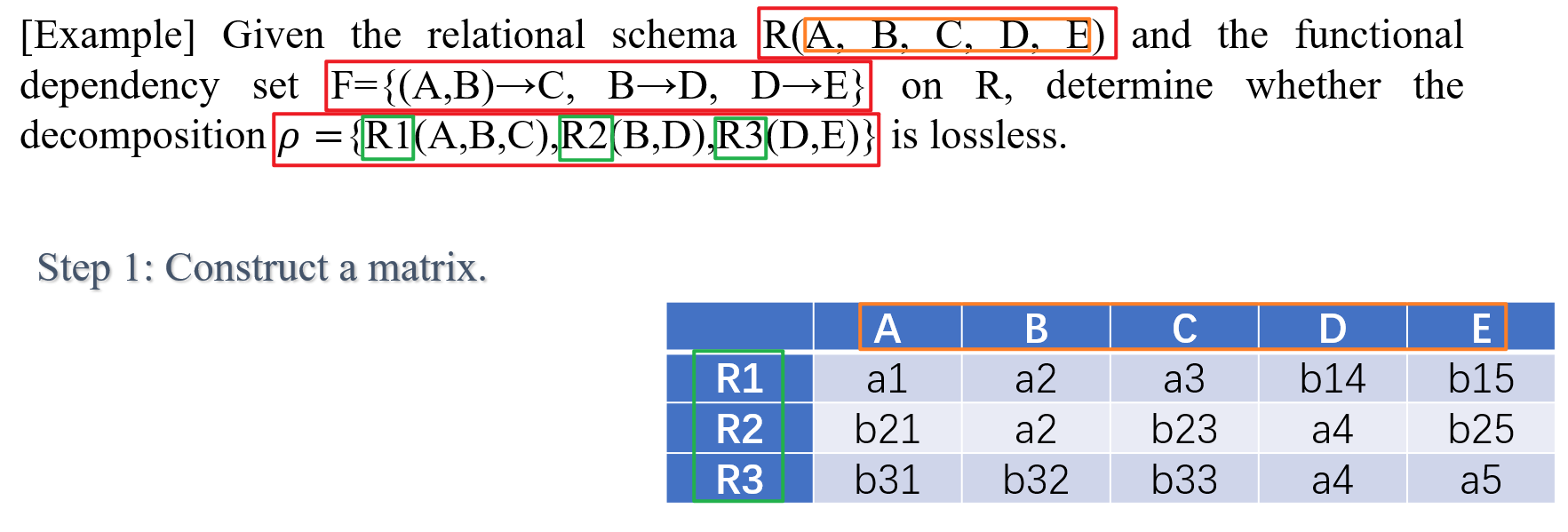
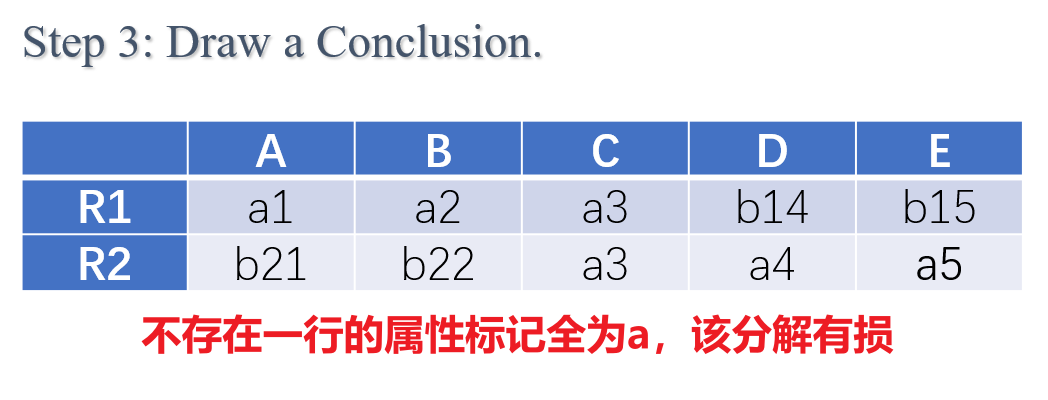
• 矩阵判别法（Matrix Discriminant Method）适用于分解为多个子模式的情况
  • 第一步：构造初始矩阵，行代表分解后的子模式，列代表所有属性，若属性属于某子模式，则对应位置标记为$a$，否则标记为 $b$
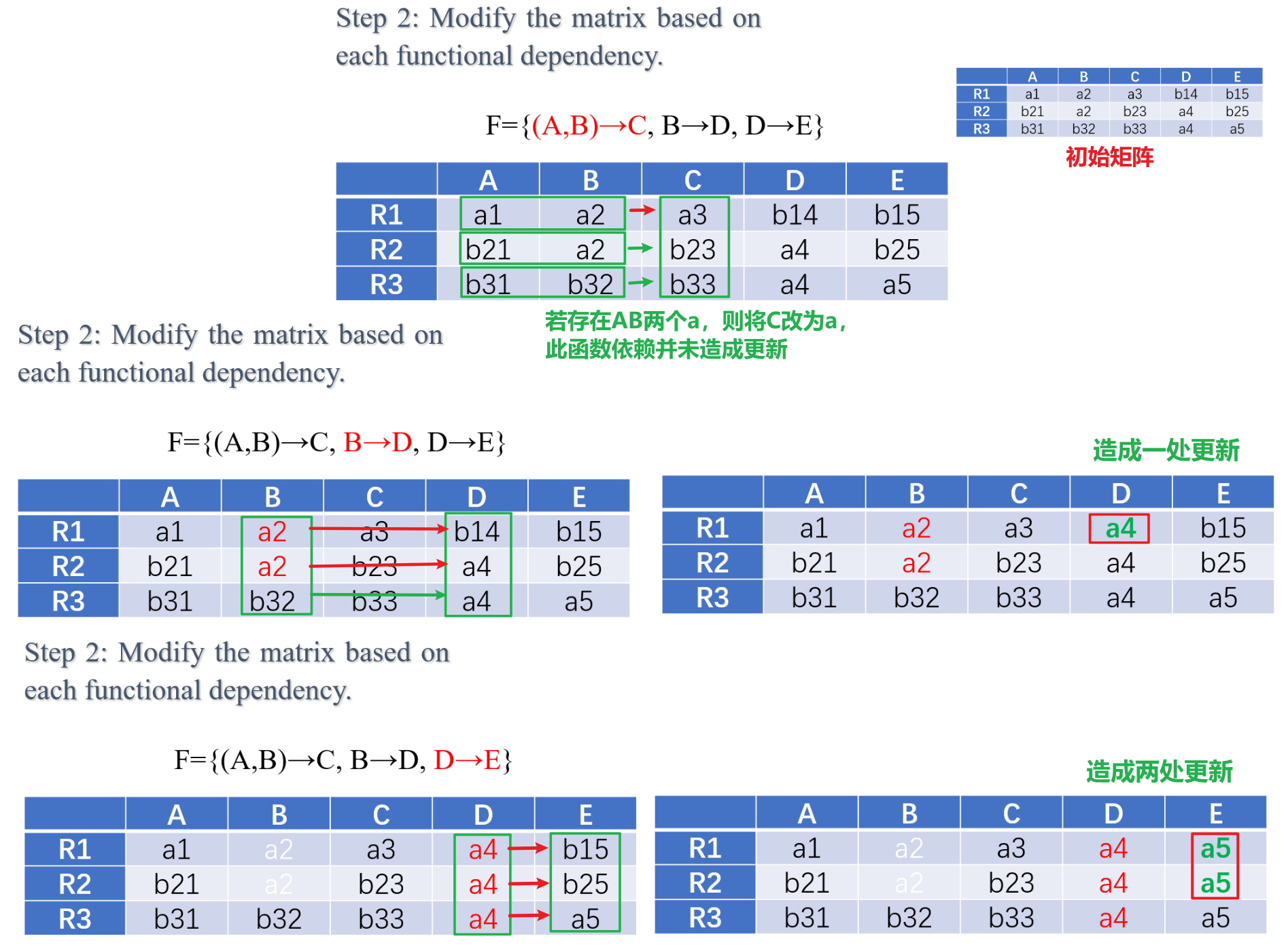
  • 第二步：根据给定的函数依赖集$F$中的函数依赖，逐条修改矩阵中的标记，若函数依赖$X→Y$成立，且某行的$X$标记为$a$，则将改行在$Y$上的标记更新为$a$
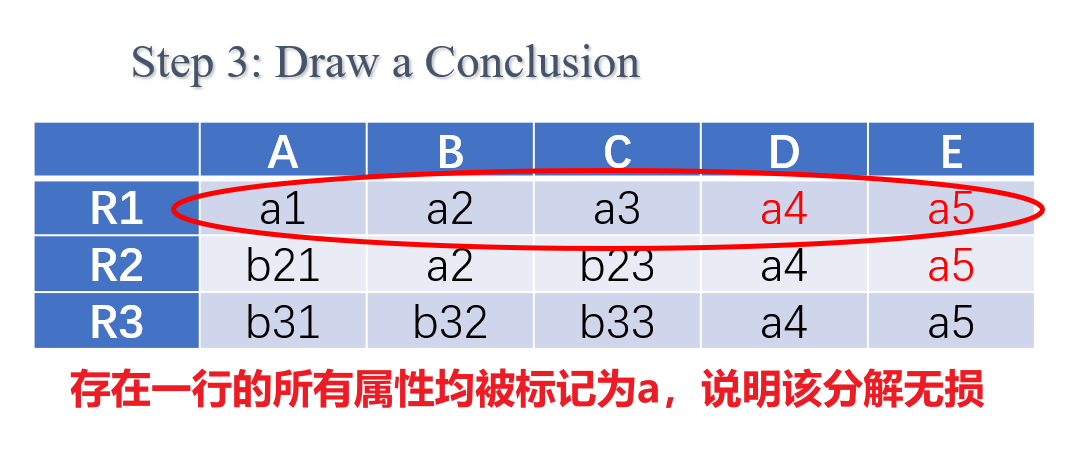
  • 第三步：若最终矩阵中存在一行全为$a$，则分解是无损的，否则不是
• 以下是一个判断为无损分解的例子

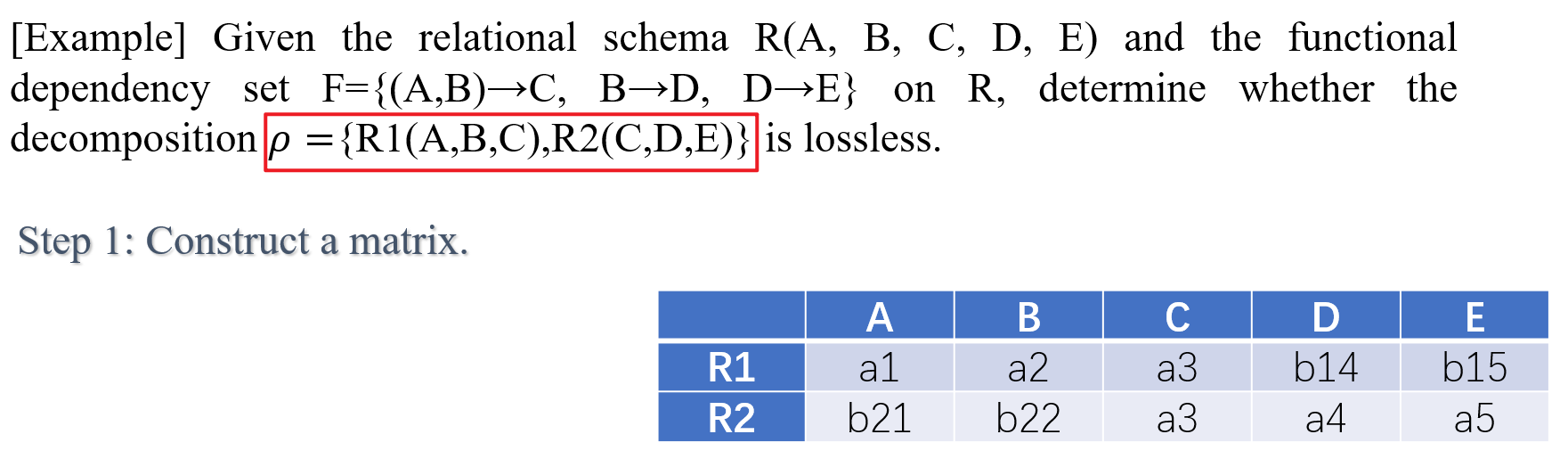
• 以下是对于同一个$R$和$F$的一个非无损分解的例子

3.3.2.2 无损连接测试定理

• 无损连接测试定理（Lossless-Join Testing Theorem）适用于分解为两个子模式的情况
  • 对于分解$\rho={R_1,R_2}$，若$R_1\cap R_2\rightarrow (R_1−R_2)$或$R_1\cap R_2\rightarrow (R_2−R_1)$成立，则分解是无损的，该方法只需求交集和差集即可

3.4 确保依赖保持

3.4.1 依赖保持的意义

• 如果分解不保持函数依赖，容易导致
  • 分解后的子模式表中的插入异常、删除异常等
  • 无法通过子模式恢复原原模式的完整约束

3.4.2 依赖保持的判别

• 属性关联法（Attribute Correlation Method）
  • 若对于原关系模式$R$的函数依赖集$F$内的任意的函数依赖$A\rightarrow B$，在分解后的子模式中都存在至少一个同时包含$A$和$B$的子模式，那么原模式的函数依赖就被成功保持了

四、关系模式的范式

要注意所谓关系完整性约束是为了确保关系模式中某种属性取值的正确与合理（关注的是细节），而此处所说的范式则是为了确保整体关系模式的合理性与安全性（关注的是整体），注意区分二者

4.1 范式的定义

• 范式（Normal Form, NF）是关系数据库设计中的应当遵循的标准化规则，用于减少数据冗余、避免数据异常（如插入、删除、更新异常）
  • 第一范式（1NF）：目的是消除复合属性
  • 第二范式（2NF）：在1NF基础上消除偏函数依赖
  • 第三范式（3NF）：在2NF基础上消除传递性的函数依赖
  • 鲍依斯科德范式（BCNF）：在3NF基础上避免非超键在左侧，进一步减少冗余

4.2 第一范式

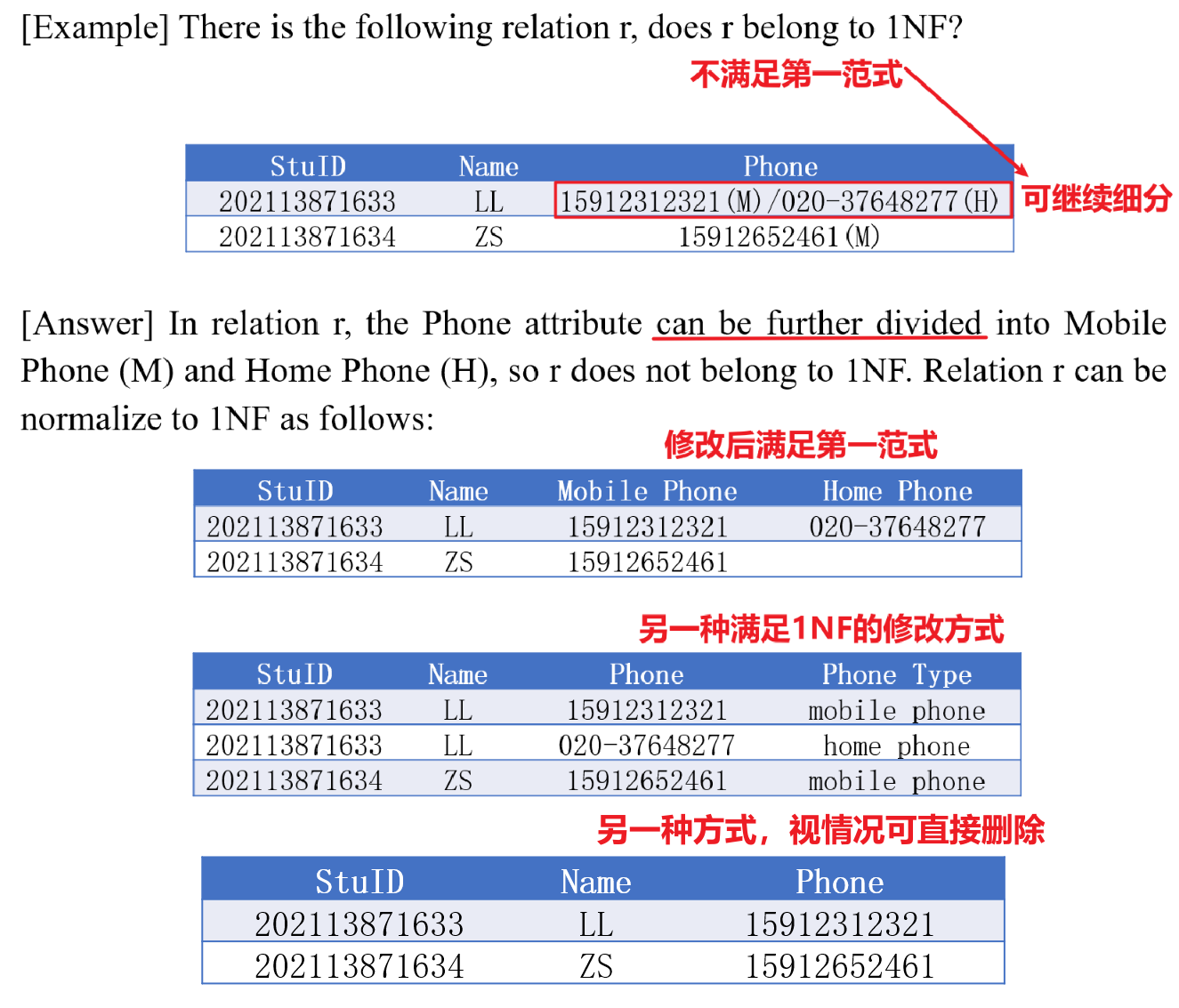
• 若关系模式$R$的每个属性都是一个不可分割的简单属性，则$R$满足第一范式（1NF）

4.3 第二范式

4.3.1 基本定义

• 对于关系模式$R$的一个函数依赖$X\rightarrow Y$，若存在一个$X$的真子集$X’\subset X$使得$X’\rightarrow Y$成立，则称$Y$偏依赖（Partial Dependet）于$X$
• 第二范式（2NF）指的是关系模式$R$在1NF基础上，其所有不可分的的非主键属性（主键是更严格的候选键）均应当完全依赖（而不是偏依赖）于该关系模式的某一个候选键

4.3.2 模式分解

• 若某关系模式$R$不遵循2NF，则应当将其分解为若干遵循2NF的子关系模式才行

4.4 第三范式

数据库设计时至少要保证所构造的关系模式至少符合第三范式

4.4.1 基本定义

• 传递依赖（Transitively Depend）指的是关系模式$R$的一个非主键属性$Z$通过另一个属性$Y$作为中介，间接依赖于某个候选键$X$，这需要满足以下条件
  • $R$拥有函数依赖$X\rightarrow Y$和$Y\rightarrow Z$
  • $Y\rightarrow X$不成立（若成立，则$X$和$Y$是等价的候选键，例如学生学号和身份证号，此时$Z$直接依赖于候选键$Y$而非间接）
  • $Z$不是$Y$的子集（若是子集则说明$Y\rightarrow Z$是平凡函数依赖，无实际语义和考虑价值）
• 第三范式（3NF）指的是关系模式$R$在满足2NF的基础上，其任意一个非主键的单个属性都不传递依赖于任意一个候选键

4.4.2 模式分解

• 若不满足3NF，则需将关系模式分解，使得分解所得子模式均满足3NF即可（若子模式存在不满足的，则继续分解直至满足）

• 以下是更通用的算法流程，能将输入的关系模式$R$依照其最小覆盖$F_{min}$（即其最简的函数依赖集）按照无损连接和保持依赖的原则，分解为若干符合3NF的子关系模式

• 以下是关于上述算法的另外两道例题

4.5 BCNF范式

4.5.1 基本定义

• 鲍依斯科德范式（BCNF）指的是关系模式$R$在满足3NF的基础上，规定所有非平凡（即函数依赖的右侧不是左侧的子集）的函数依赖的左侧都必须是候选键，不允许任何非超键决定其他属性，以消除非超键->属性导致的冗余

4.5.2 模式分解

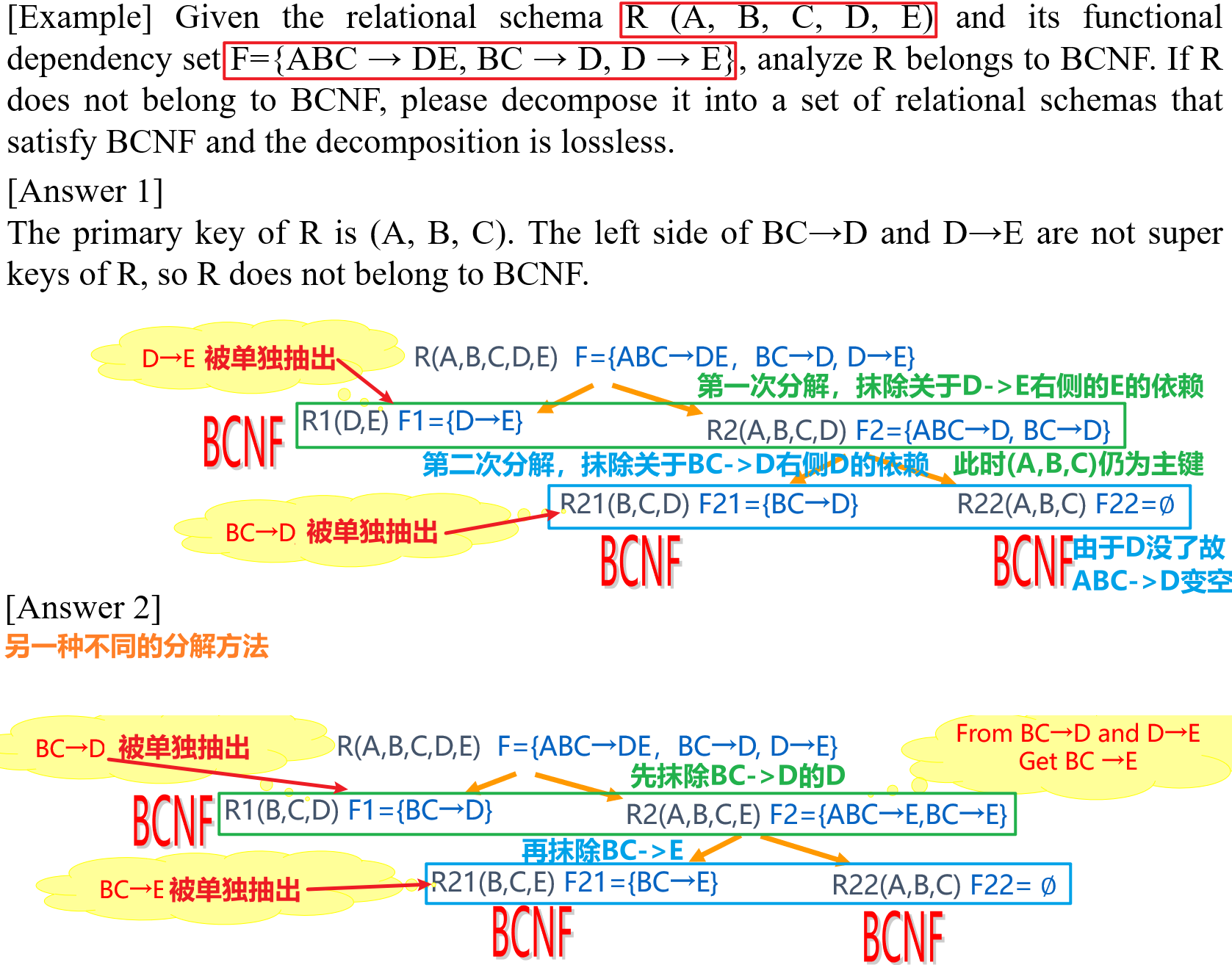
• 当关系模式$R$不满足BCNF时，应当将其分解为满足BCNF的子模式，以下是通用的算法
  • 要注意该分解过程中只能保证无损，而无法保证全部函数依赖关系的保有（而前文提到的分解为符合2NF/3NF的子模式，是能同时保证无损和依赖保有的）
  • 因为BCNF规定函数依赖的左侧不能是非超键，故分解过程中会将那些左侧为非超键的函数依赖拆开，导致寒素依赖被破坏

• 以下是一道例题，以两种方法进行分解