文章

关于数据库系统以及三层数据模型

简单介绍DBS/DBMS/DB的概念、DBS的三级模式与两层映射、重点介绍三层数据模型中的概念数据模型（E-R模型）与逻辑数据模型（关系模型以及与其相关的关系代数）

发表于 更新于
作者 WhythZ
39 分钟阅读
关于数据库系统以及三层数据模型

一、关于DBS

1.1 DBS的核心概念

1.1 数据库DB

  • 数据库（DB, Database）是按照数据结构组织和存储数据的仓库，本质上是数据集合，存储在计算机存储设备上

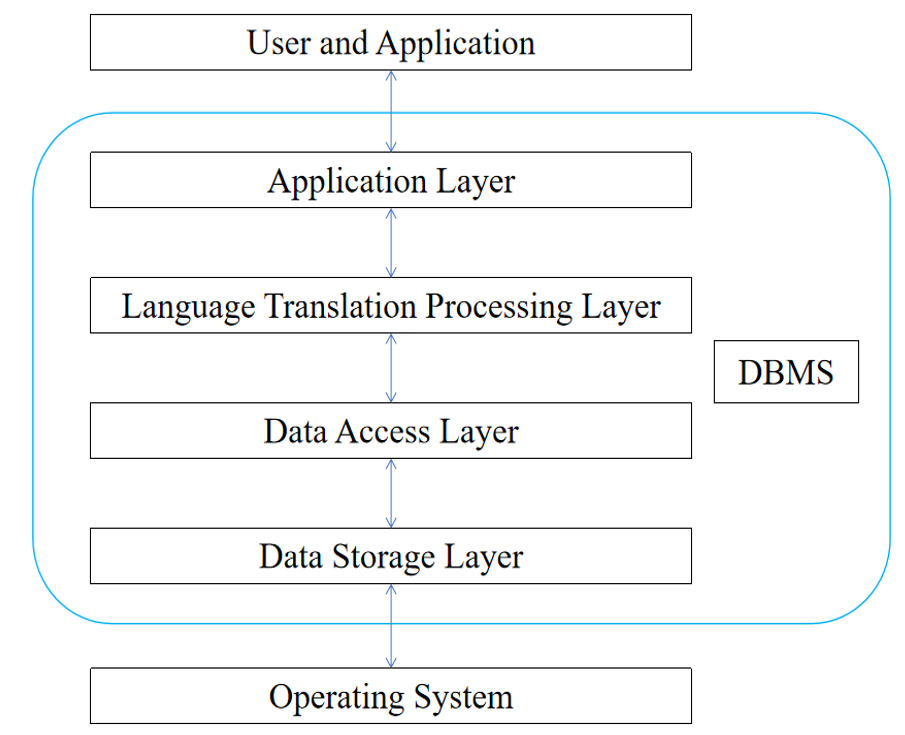
1.2 数据库管理系统DBMS

  • 数据管理系统（DBMS, Database Management System）是管理数据库的软件，用于建立、使用和维护数据库（例如MySQL、Oracle、openGauss等关系型数据库软件，还有些非关系型的）
    • 提供基础的增删改查（CRUD）操作，即增Create、查Read、改Update、删Delete

DBMS的层次结构.png

1.3 数据库管理员DBA

  • 数据库管理员（DBA, Database Administrator）通过DBMS来管理DB
    • 负责整个DBS的规划、设计、实施、维护、优化以及数据安全

1.4 数据库系统DBS

  • 数据库系统（DBS, Database System）是一个更广泛的概念，主要包括以下部分
    • 数据库（DB）
    • 软件（DBMS）
    • 硬件（存储设备等）
    • 用户（权限有所不同）

1.5 四者间的关系

  • DB是存储数据的实体
    • 相当于图书馆中的书籍，即数据本身
  • DBMS是管理DB的自动化软件
    • 相当于图书管理员，依据规则管理图书数据
  • DBA是管理、维护和优化DBS的高层
    • 相当于图书馆的馆长，决定图书馆的布局（数据库结构）、书籍分类规则（数据模型）、采购哪些书籍（数据需求）等更高层的事务
  • DBS是整个运行环境
    • 相当于整个图书馆本身，包括建筑（硬件）、书籍（数据库）、管理员（软件）等一切

1.2 DBS的三级模式

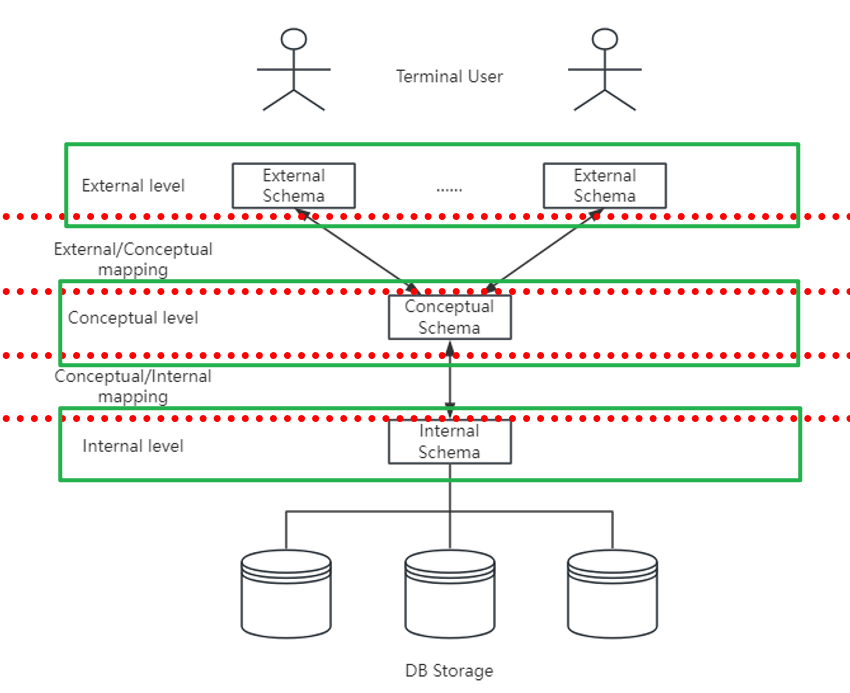
1.2.1 三级模式

  • 外部模式/用户模式（Eternal Schema/User Schema）
    • 描述数据库用户可见可用的局部数据的逻辑结构和特性
  • 概念模式（Conceptual Schema/Schema）
    • 是描述数据库中所有数据的逻辑结构和特征的全局视图
  • 内部模式（Internal Schema）
    • 整个数据库的最低层级表示，用于描述数据库数据的物理结构和存储方式

DBS的三级模式.png

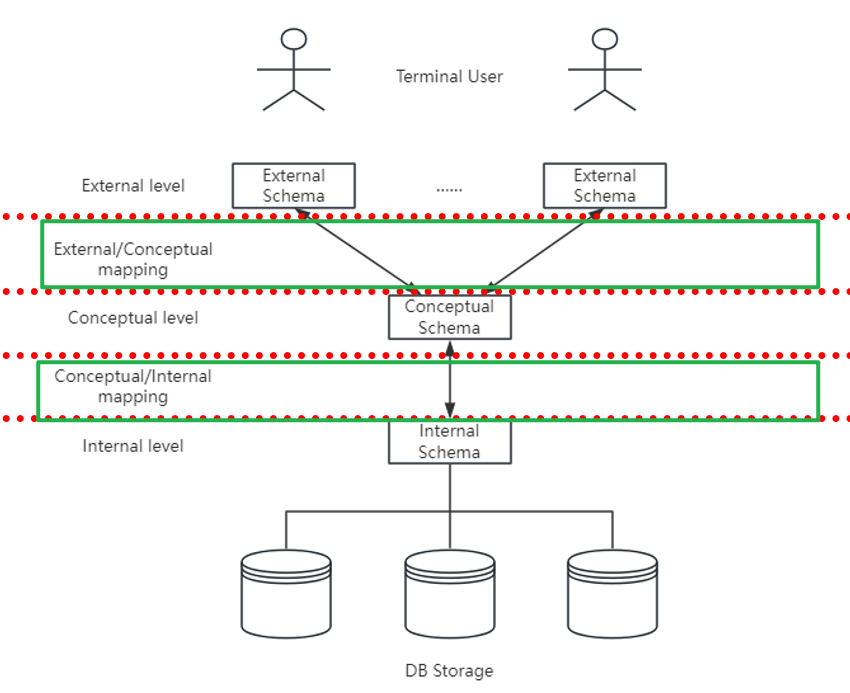
1.2.2 两层映射

  • 外部模式-概念模式映射（External Schema-Conceptual Schema Mapping）
    • 确定数据的局部逻辑结构与全局逻辑结构之间的对应关系
  • 概念模式-内部模式映射（Conceptual Schema-Internal Schema Mapping）
    • 确定数据的全局逻辑结构与存储结构之间的对应关系
    • 一个数据库可有多个外部模式，但概念模式和内部模式各自只能有一个

DBS的两层映射.png

1.2.3 数据独立性

  • 在数据库的三级模式架构中，数据独立性（Data Independence）指的是修改某一层级的模式而不会导致上层模式也随之改变
    • 外部模式-概念模式映射保证了数据的逻辑独立性（Logical Independence）
      • 当数据的整体逻辑结构发生变化时，数据的局部逻辑结构保持不变
      • 保护应用程序不受全局逻辑结构（中层的逻辑模式）变化的影响（全局逻辑结构被修改时，不影响应用程序，因其基于数据局部逻辑结构编写）
    • 概念模式-内部模式映射保证了数据的物理独立性（Physical Independence）
      • 当数据的物理存储结构发生变化时，数据的逻辑结构保持不变
      • 保护应用程序和逻辑结构不受物理存储（底层的内部模式）变化的影响（物理存储结构被修改时，不影响应用程序，因其基于数据局部逻辑结构编写）

1.3 DBS对比文件系统

特质/系统类型数据库系统（DBS）普通文件系统（File System）
数据结构化（Structuring）低高
数据共享（Sharing）低高
数据冗余（Redundancy）高低
数据独立性（Independency）低高
用户交互界面（User Interface）单一多样
数据统一管理（Unified Management）无有

二、关于数据模型

2.1 数据表示与处理

  • 所有的数据都可以直接或间接使用二进制数字表示，例如IEEE浮点数和ASCII字母等，而数据经过处理分析后，才能得到具有特定含义、可用于决策或知识获取的有效信息
    • 数据处理的空间分布方式（Space Distribution）
      • 集中式处理（Centralized Processing）：数据集的存储和处理交给单个计算机完成
      • 分散式处理（Decentralized Processing）：数据集被分区（Partition）存储在多个计算机之中，这些计算机间相互独立并不进行通信，独立管理和操作数据
      • 分布式处理（Distributed Processing）：数据集被分块（Block）存储在多个计算机之中，这些计算机间通过网络互联
    • 数据处理的时间分配方式（Time Allocation）
      • 批处理（Batch Processing）：对每组特定数据进行批量处理
      • 在线处理（Online Processing）：
        • 实时处理（Real-time Processing）：接收到输入数据后，立刻处理得出结果
        • 延迟处理（Delayed Processing）：先存储输入数据，间隔一定时间后再进行处理

2.2 数据模型与模式

2.2.1 数据模型的组成

  • 大量数据以一定结构组织形成数据模型（Data Model）才能被理解、处理、分析
    • 文档模型：例如JSON的键值对嵌套结构
    • 关系模型：例如表格的行列结构
  • 数据模型通常需包含以下组成部分
    • 数据结构：数据的静态特性，描述数据库的组成对象及其间的联系
    • 数据操作：数据的动态特性，提供对数据库的组成对象的增删改查
    • 完整性约束：即一组用于限制数据状态的变化的规则集合

2.2.1 数据模式的概念

  • 数据模式（Data Pattern）指的是表示同一类数据模型的通用模板（从具体数据中提炼）

两种关系模型的数据模式.png

2.3 数据模型的层次

  • 数据模型分为三个层次
    • 概念数据模型（Conceptual Data Model）
      • 不涉及信息在计算机系统当中的表示的模型来描述问题
      • 适用于无需了解底层实现的终端用户
    • 逻辑数据模型（Logical Data Model）
      • 直接面向数据库的逻辑结构
      • 适用于需用严格的数据库语言来定义和操纵数据的设计者
    • 物理数据模型（Physical Data Model）
      • 直接描述数据在磁盘或磁带上的存储方式和存取方法
      • 适用于需要将设计者的设计方案真正在计算机系统中实现的程序员

2.4 逻辑数据模型

2.4.1 三要素

  • 逻辑数据模型包括三个要素
    • 数据结构（Data Structure）：解决数据和联系如何表达、怎样实现等问题
    • 数据操作（Data Operation）：对数据库的检索和更新操作的实现
    • 完整性约束（Integrity Constraint）：数据及其间的关系应具有的制约和依赖规则，从而保证数据库中的数据是正确的
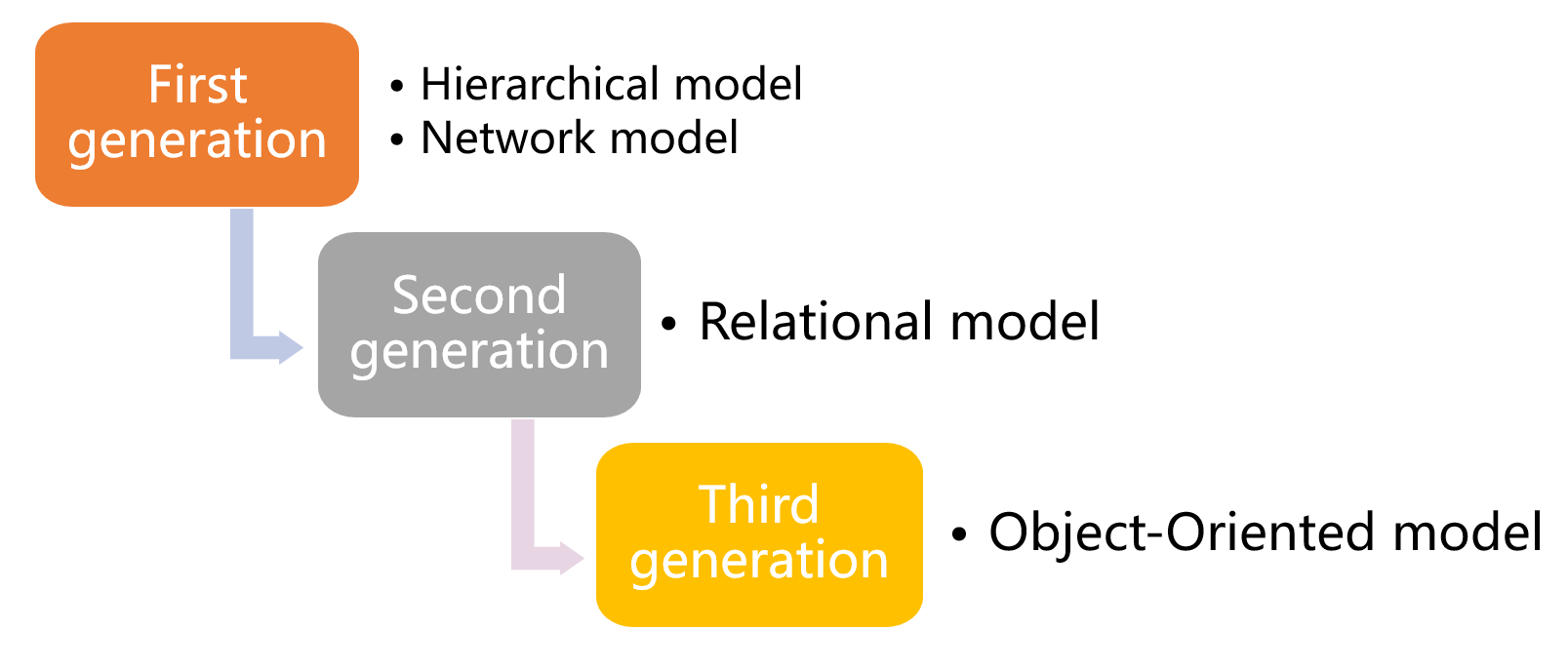
  • 逻辑数据模型到目前为止的发展历程中主要有四类模型

逻辑数据模型的发展阶段.png

2.4.2 层次模型

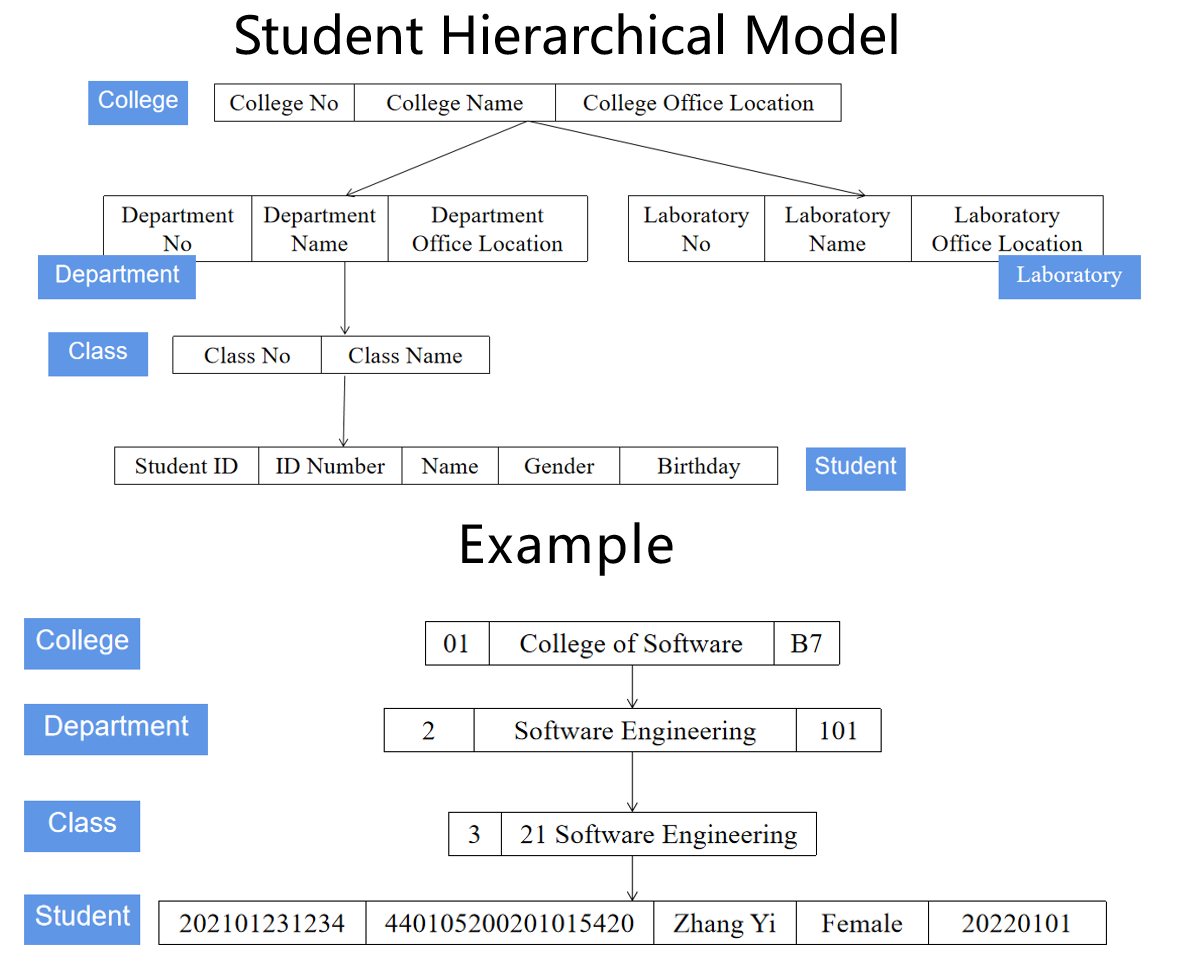
  • 层次模型（Hierarchical Model）是一种逻辑数据模型，其用倒立有向树的数据结构表示各类实体及其间的联系，IBM研发的IMS是采用层次模型的数据库的典型代表
    • 树中的每个结点表示一个记录类型（描述的是实体），结点间的边表示记录类型间的关系
    • 每个记录类型可包含若干个字段（描述实体的属性），各个记录类型及其字段都必须命名
    • 若要存取某一记录型的记录，可以从根节点起，按照有向树层次向下查表
  • 例如下图中的学生身份的描述，采用的就是层次模型，从包含多个属性字段的College类型向下选择，有Department和Laboratory两个分支方向

层次模型的示例.png

  • 层次模型的完整性约束体现在对特定操作的约束上
    • 插入操作：在插入任何子节点记录之前，其对应的父节点记录必须已存在于数据库中，以确保不会出现没有父节点的孤立子节点（例如一转校生还未被分配具体的班级父节点时，该学生就不能被纳入数据库，除非后续分配了班级才能够被插入）
    • 删除操作：父节点被删除后，其子节点也会被一并删除而不会残留，防止孤立节点产生
    • 更新操作：更新某项数据时，所有与其相关联的数据应当一并被更新
  • 层次模型的优缺点如下
    • 优点
      • 清晰简单的数据结构
      • 较高的访存效率
      • 较好的完整性约束
    • 缺点
      • 表示复杂系统的能力有限
      • 数据独立性差

2.4.3 网状模型

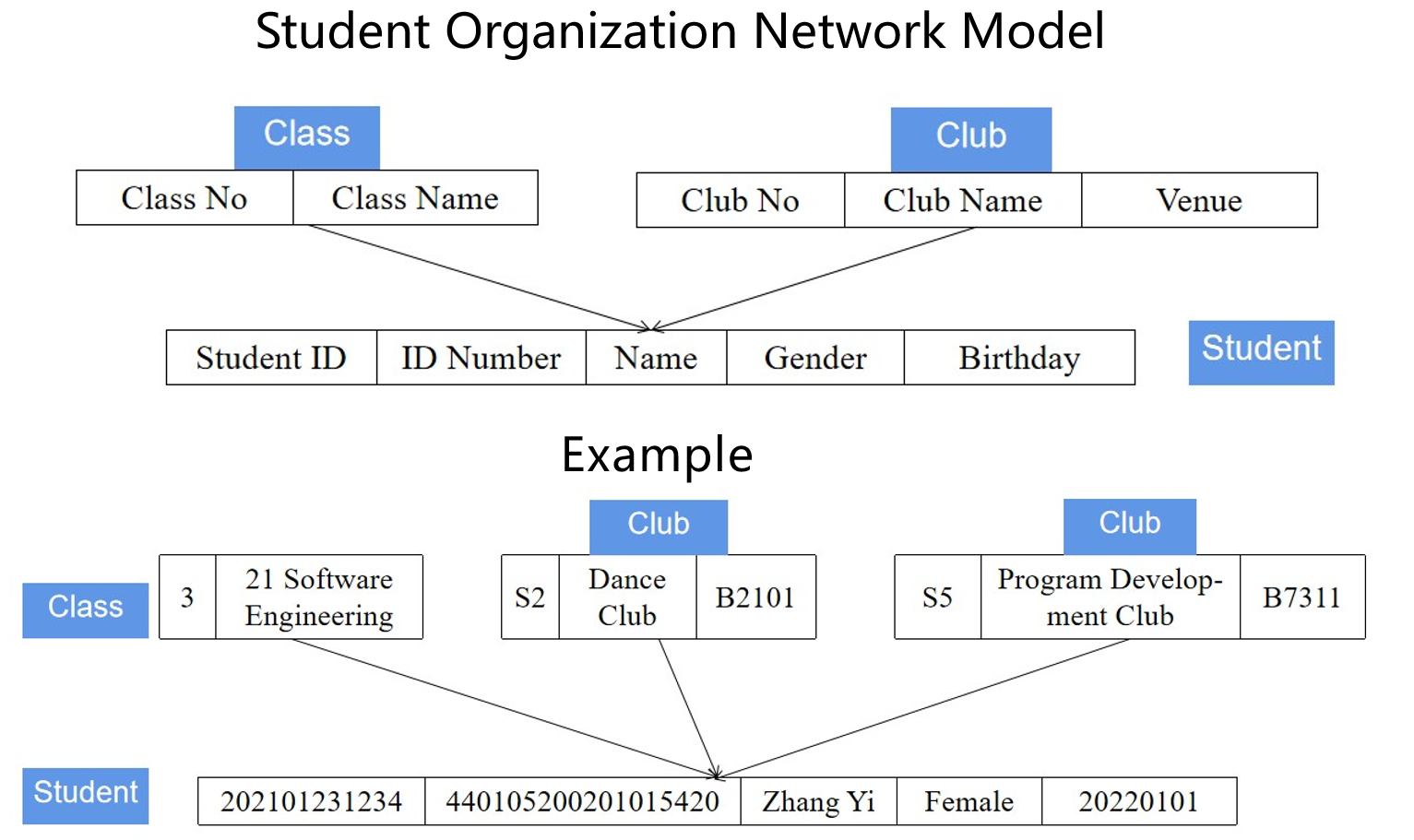
  • 网状模型（Network Model）用有向图结构以有向图的数据结构表示实体类型及其实体之间的联系，从定义能看出，层次模型中的父子结点间的联系唯一，而网状模型中父子关系可以不唯一
    • 每个结点表示一个记录型（实体）
    • 每个记录型可包含若干个字段（实体属性）
    • 结点间的连线表示记录型（实体）间的父子关系
  • 例如下图中的学生身份的描述，一个Student可以同时被Class对象或多个Club对象所指向

网状模型示例.png

  • 网状模型的完整性约束也体现在对特定操作的约束上
    • 插入操作：即便所有的父节点未被完全确定，某新增节点也可以被直接插入数据库中（例如一个已经确定班级的转校生，即使还未分配社团，其仍被允许插入数据库中）
    • 删除操作：一个父节点允许被单独删除（例如某个社团删除了，那么其原有团员学生并不会被删除掉，其仍归属于其它社团或班级而存在）
    • 更新操作：更新某个节点时，只有特定节点会被更新，而无需更新其它相关联的节点
  • 网状模型的优缺点如下
    • 优点
      • 能够描述更复杂的数据及其间关系
      • 节点间的关系简单，灵活性高，访存效率高
    • 缺点
      • 数据结构较为复杂
      • 数据独立性差

2.4.4 关系模型

  • 层次数据库和网状数据库在数据独立性和抽象级别上仍有不足，用户在对这两种数据库进行存取时，仍需明确数据存储结构并指出存取路径，关系数据库较好地解决了这些问题
  • 关系模型（Relational Model）的完整性约束有以下内容
    • Entity Integrity
    • Referential Integrity
    • User Defined Integrity
  • 关系模型的优缺点如下
    • 优点
      • 关系数据库语言是非过程化的，提高了数据独立性，大大降低了用户编程的难度
      • 数据操作是基于集合的操作，提高了数据访问的便捷性
      • 强大的数学理论基础，清晰简单的数据结构
    • 缺点
      • 复合属性通常需要拆分为多个简单属性，可能会破坏数据之间的层次关系
      • 无法表示可变长度属性
      • 对系统性能提出了更高的要求

2.4.5 面向对象模型

  • 面向对象模型（Object-Oriented Model）用更接近人类通常思维的方式建立问题模型，并进行结构模拟和行为模拟，使得设计出的软件能尽可能直接表现出问题的求解过程，具体参考C++编程

三、E-R模型

实体-关系模型（E-R Model, Entity-Relationship Model）是一种概念数据模型

3.1 实体与关系

  • 实体相关的核心概念有
    • 实体（Entity）：客观存在且可区分的事物（例如学生）
    • 实体型（Entity Type）：对同类实体的抽象描述，包含属性定义（例如”学生”称谓）
    • 实体集（Entity Set）：同一实体型的（Homogeneous）实例集合（例如班级）
    • 属性（Attribute）：描述实体所拥有的特征（例如年龄）
    • 唯一标识符（Identifier）：能唯一标识实体的属性或属性组（例如学号）
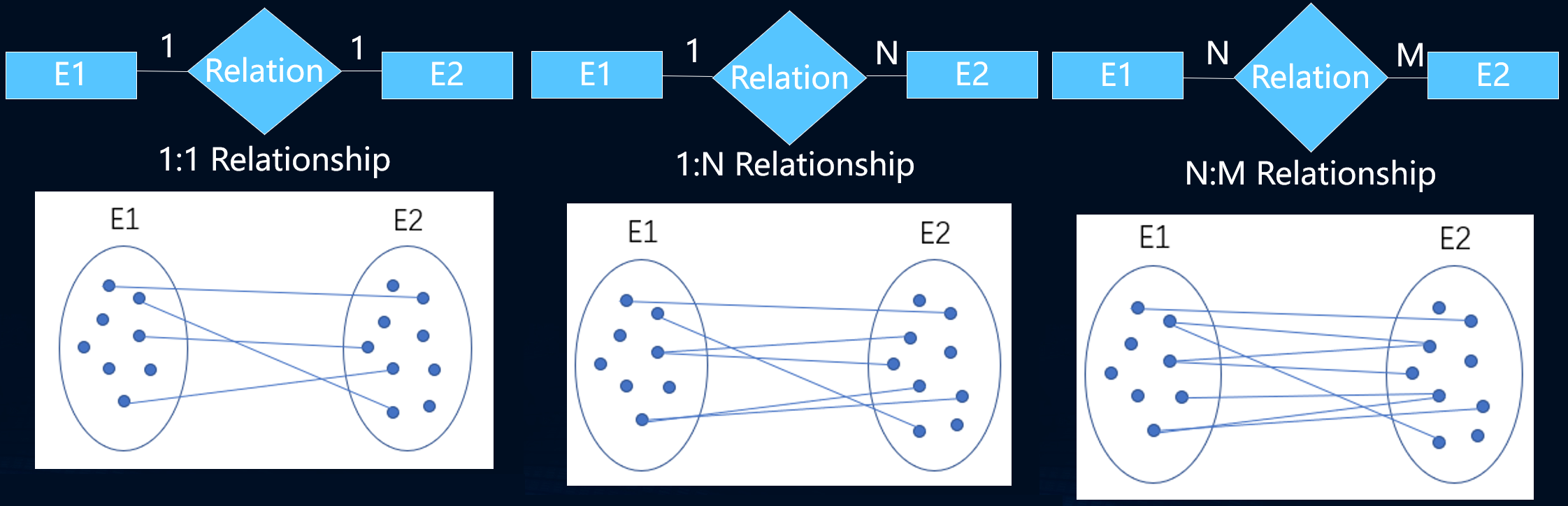
  • 不同实体型的对象（数据）间的关系可表现为1:1（例如班级与班主任间的关系）、1:N、N:M三种形式，下图中E1和E2是两种不同的实体型的实体集

实体与实体间的三类关系.png

  • 一对一关系（One-to-One Relationship）中
    • E1中的实体可与E2中的最多一个实体存在关系
    • E2中的实体可与E1中的最多一个实体存在关系
  • 一对多关系（One-to-Many Relationship）中
    • E1中的实体可与E2中的任意个数个实体存在关系
    • E2中的实体可与E1中的最多一个实体存在关系
  • 多对多关系（Many-to-Many Relationship）中
    • E1中的实体可与E2中的任意个数个实体存在关系
    • E2中的实体可与E1中的任意个数个实体存在关系

3.2 E-R图及其绘制

3.2.1 绘图的基本元素

  • E-R模型通常可使用E-R图（E-R Diagram）可视化表现
    • 矩形：实体型
    • 菱形：关系型
    • 椭圆：实体型或关系型的属性（下划线表示该属性是实体型的主键，即唯一标识符）
    • 直线：链接上述三者
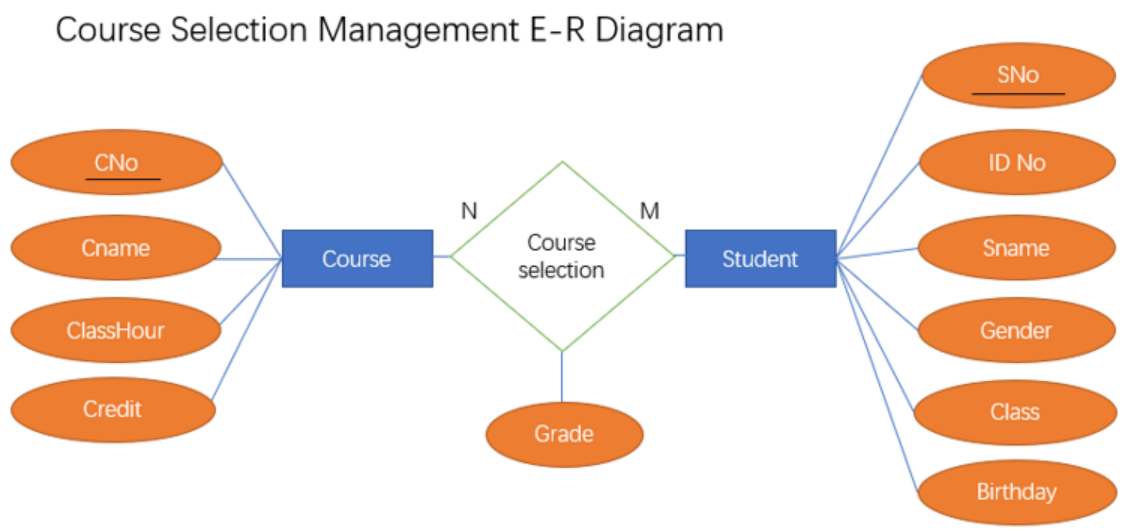
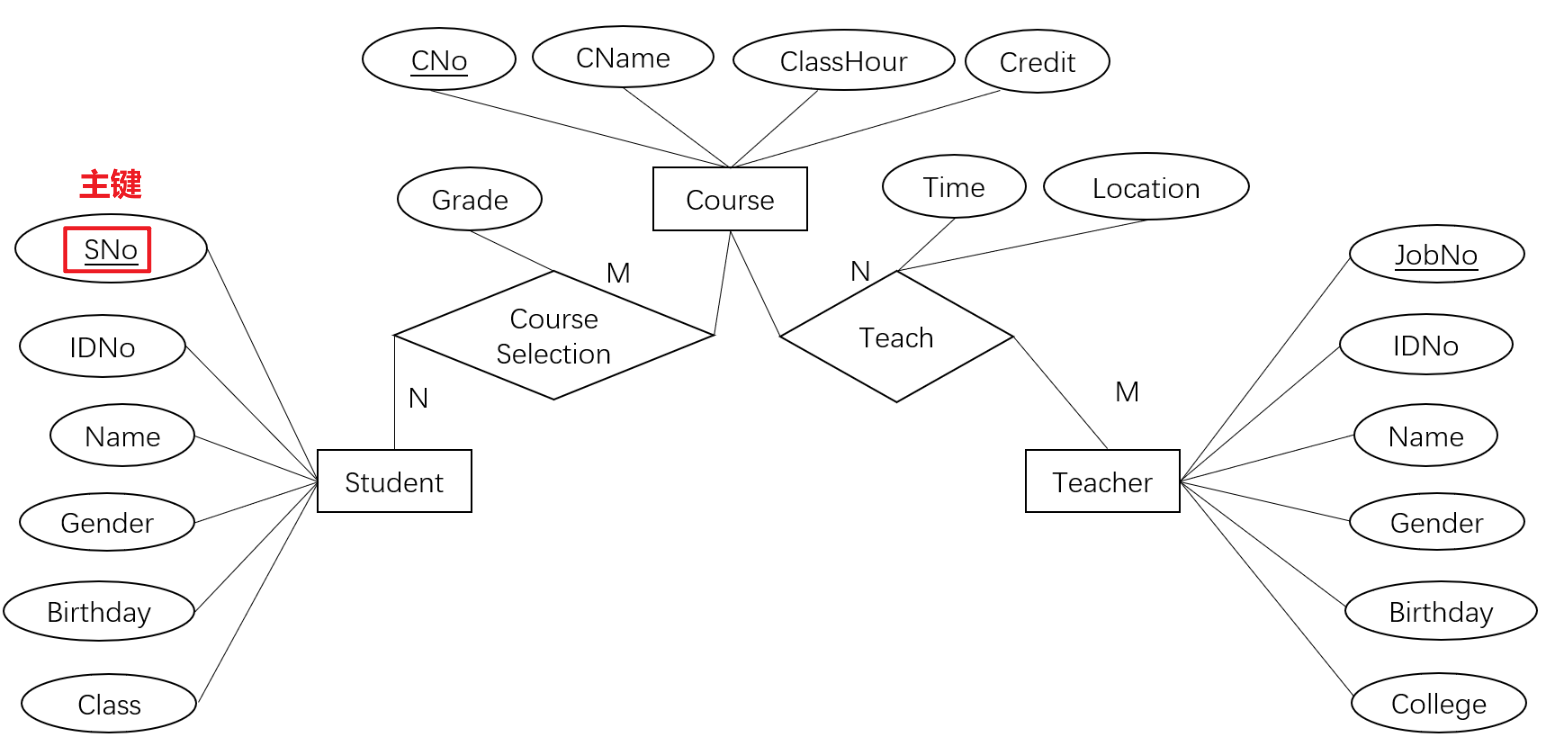
  • 如下图所示以选课表为例，表示两实体型间的关系，其中的Course Selection关系关联了两个实体型（Binary Relationship）

E-R图选课表简化示例.png

3.2.2 实体型间的单关系

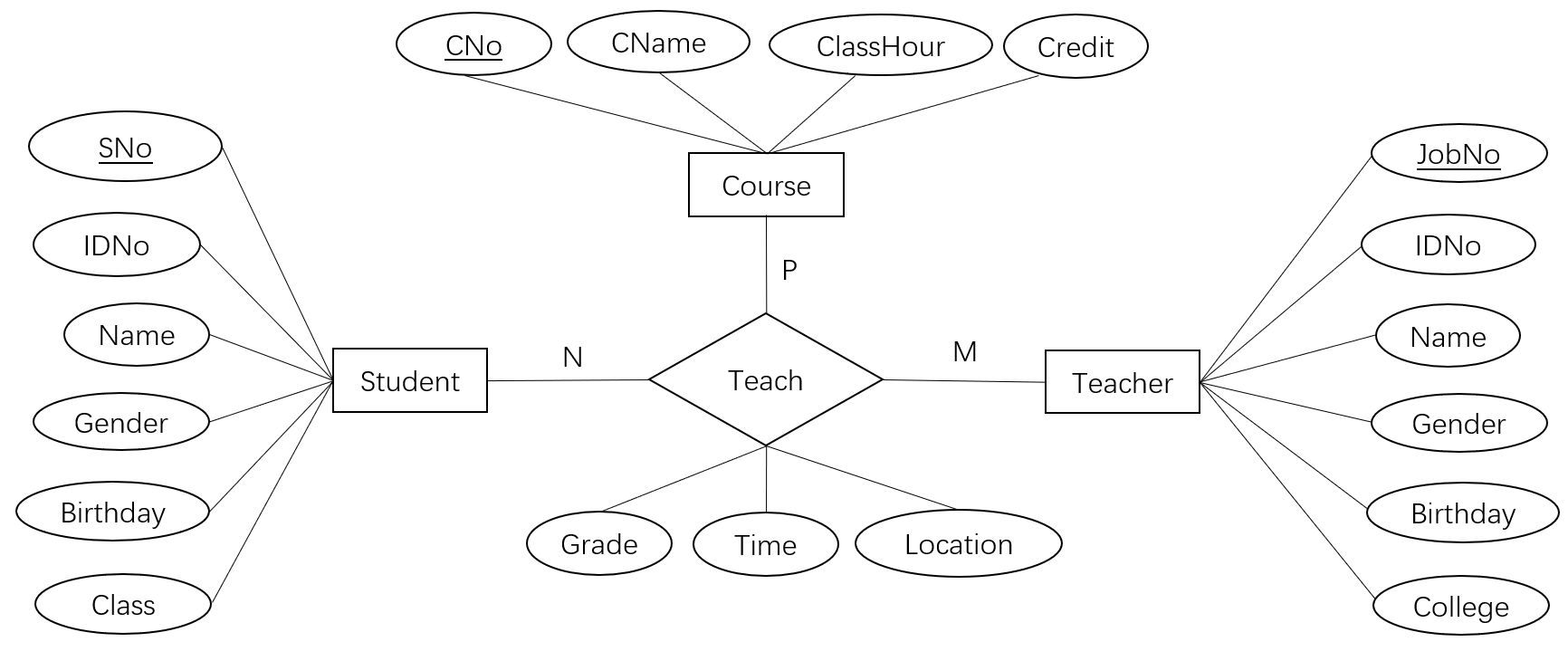
  • 上述示例中的关系可以进一步表示为如下的多实体型间的关系，其中三个实体型间通过两个关系两两链接（Binary Relationship）

E-R图选课表复杂示例.png

  • 多实体型间的关系也可表示为如下的形式，其中同一个Teach关系（Multiple Relationship）连接了两个以上的实体型

E-R图选课表Multiple关系.png

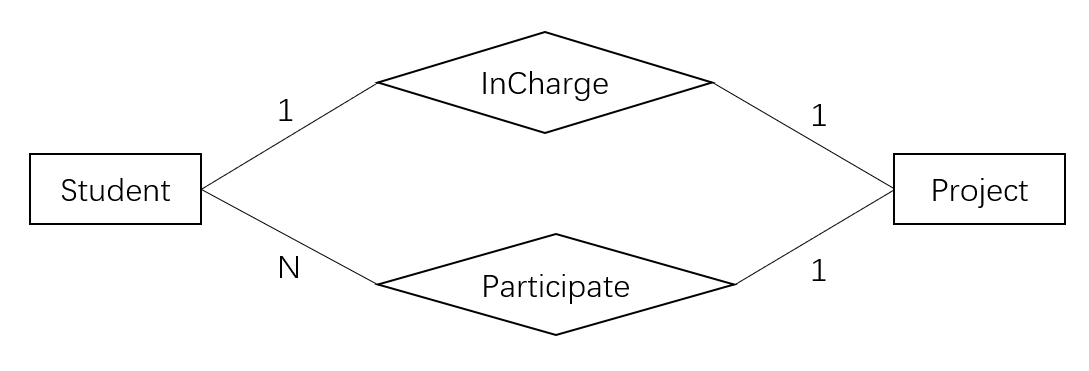
3.2.3 实体型间的多关系

  • 两个实体型间也可被多个关系连接在一起

实体型间的多关系.png

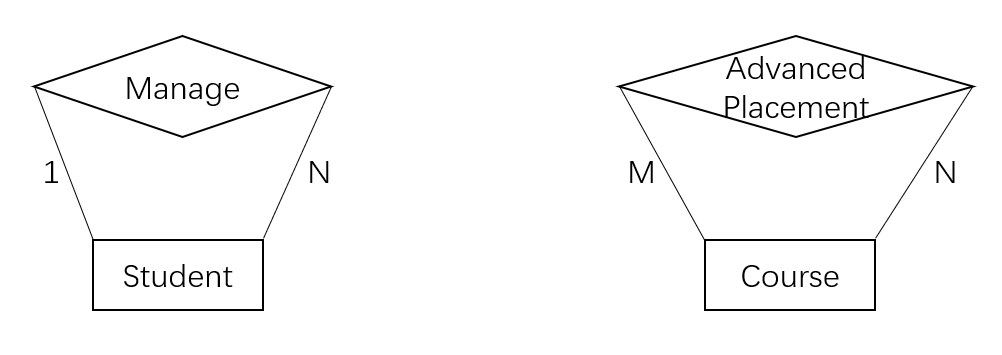
3.2.4 同一实体型间的关系

  • 同一实体型的内部也可被关系链接

同一实体型间的关系.png

3.3 属性从属的可变性

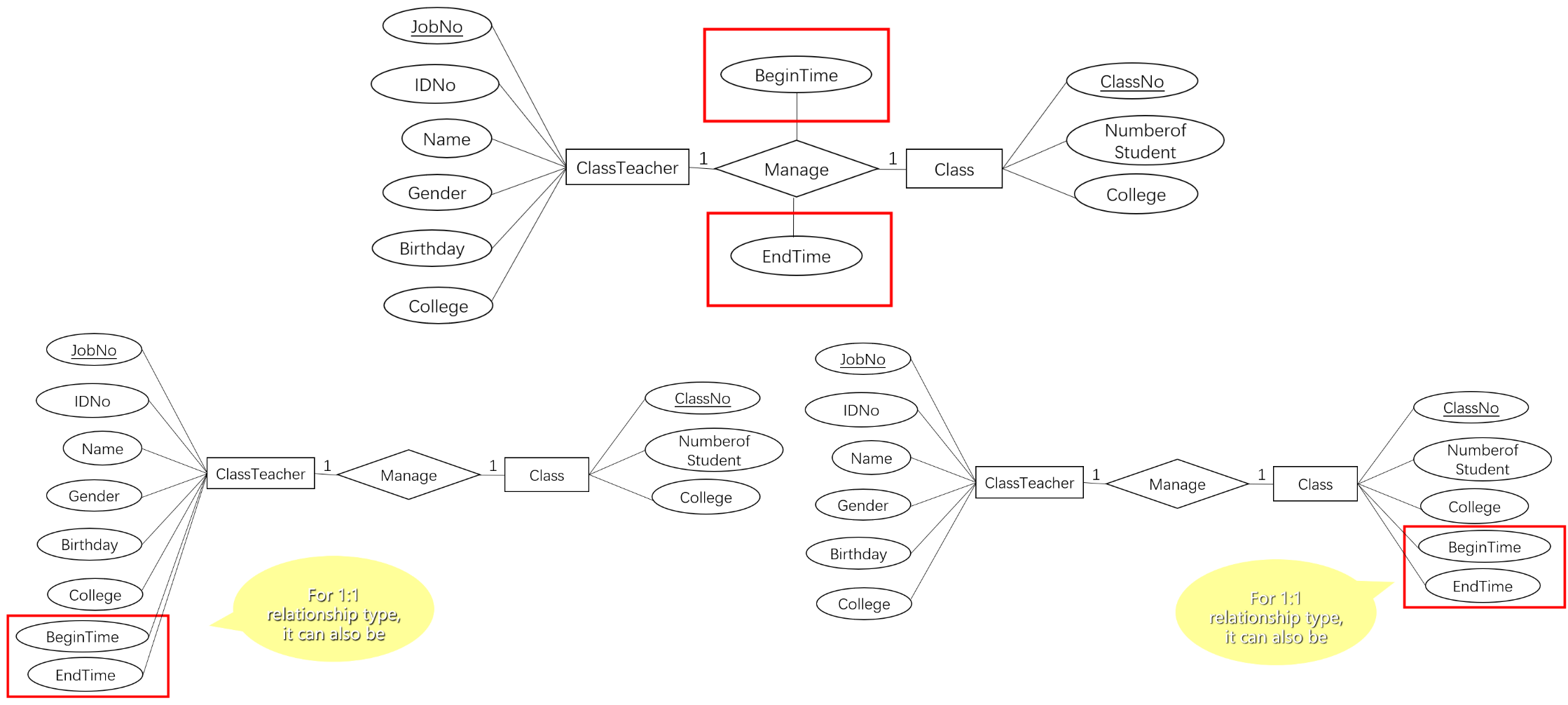
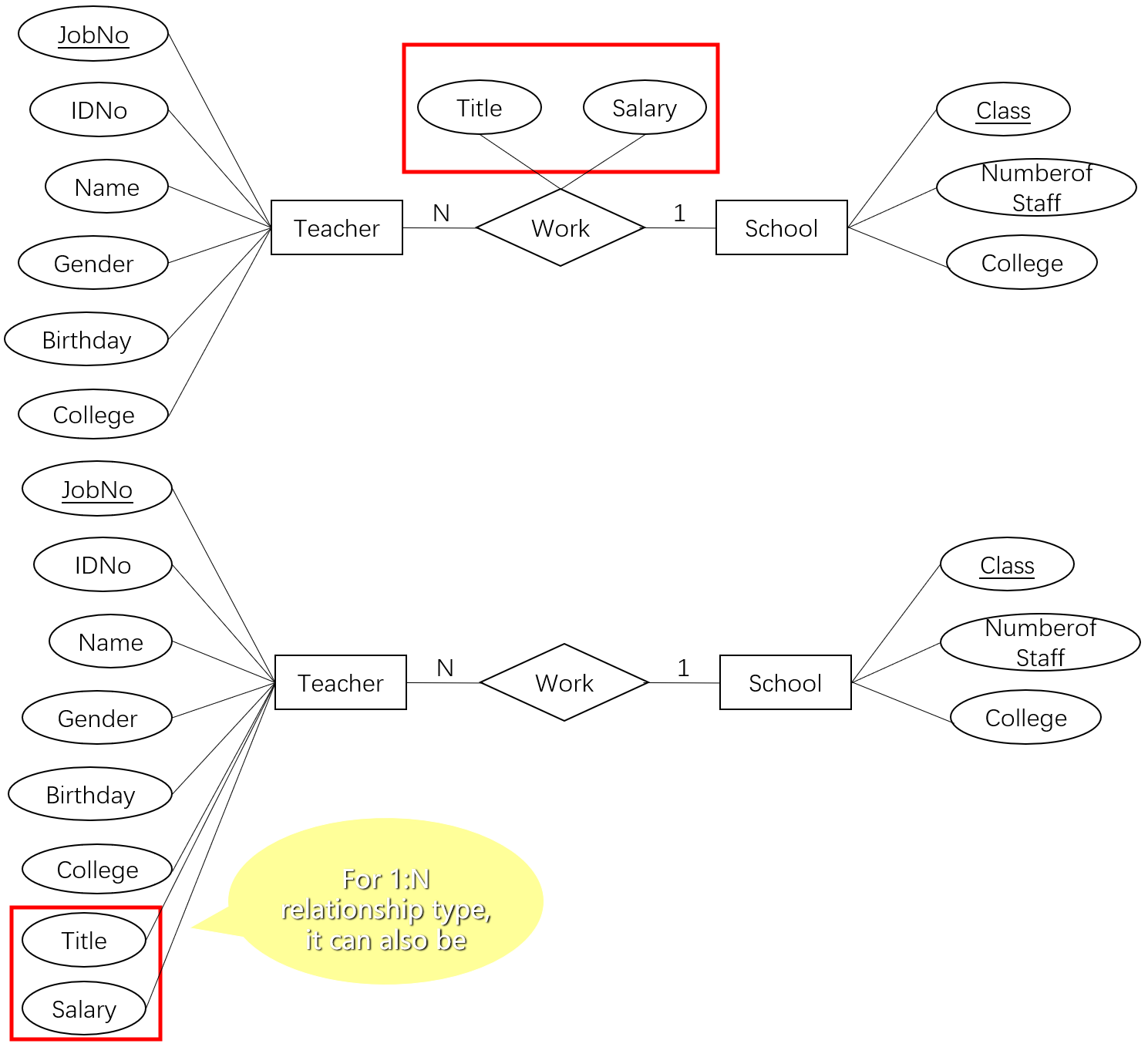
  • 在1:1关系中，关系的属性可以改属于任意一边的实体型身上而意义不变

一对一关系中的属性布局变通.png

  • 在1:N关系中，关系的属性可以改属于N一边的实体型身上而意义不变

一对多关系中的属性布局变通.png

3.4 实体或关系的强弱

3.4.1 强弱实体

  • 强实体（Strong Entity）
    • 可以独立存在
    • 有自己独立的主键，唯一性地标识它的每个实例
  • 弱实体（Weak Entity）
    • 必须依靠其它实体存在
    • 其主键包括它所依赖的实体类型的主键（即组合主键）
  • 弱实体与强实体可以相互转换，没有绝对意义上的强与弱
    • 若我们定义排课表实体的主键是组合主键（课程编号+排课编号，如CS163+01），那么其就是是弱实体，因为区别弱实体与强实体的关键在于主键
    • 但若我们定义排课编号是CS16301而不再是01，那它的主键（排课编号）就不再需要复合课程编号，它就成为了强实体

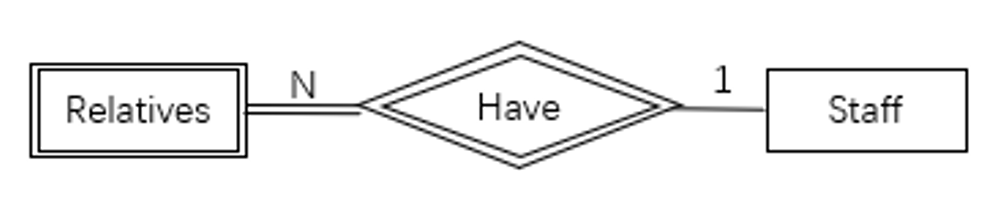
3.4.2 强弱关系

  • 强关系（Strong Relationship）即两个强实体类型间的关系
  • 弱关系（Weak Relationship）即弱实体与其依赖实体间的关系

强弱实体示例.png

  • 例如上图表示Staff拥有Relatives的关系
    • Staff是强实体
    • Relatives是弱实体
    • Have是弱关系

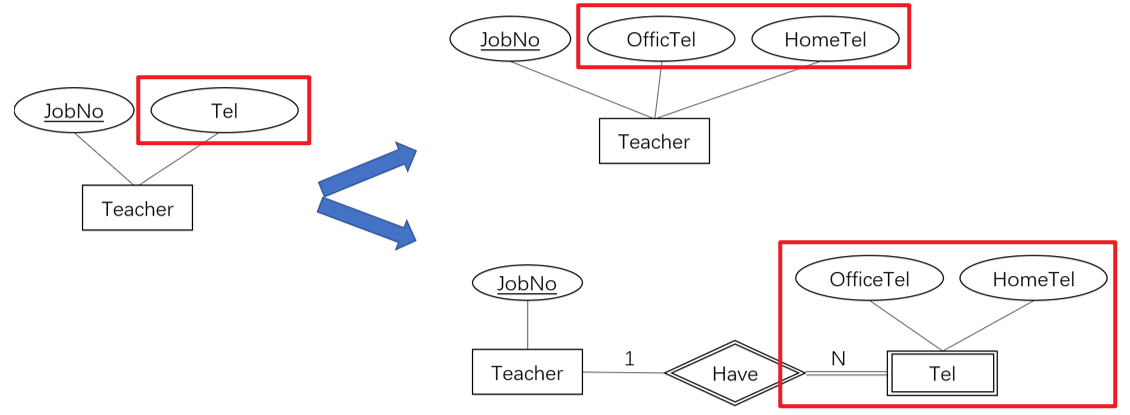
3.5 属性的多值与复合

  • 依据属性的多值与否
    • 单值属性：只能拥有唯一的值（例如学生的性别）
    • 多值属性：能有多个值（例如老师的手机号码）
  • 依据属性的简单与否
    • 简单属性：不可再细分（例如学生的性别）
    • 复合属性：可以继续细分（例如学生的地址）

多值属性与复合属性.png

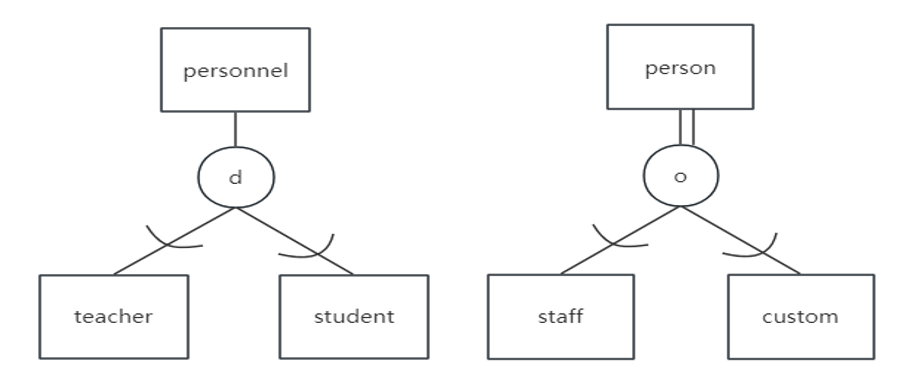
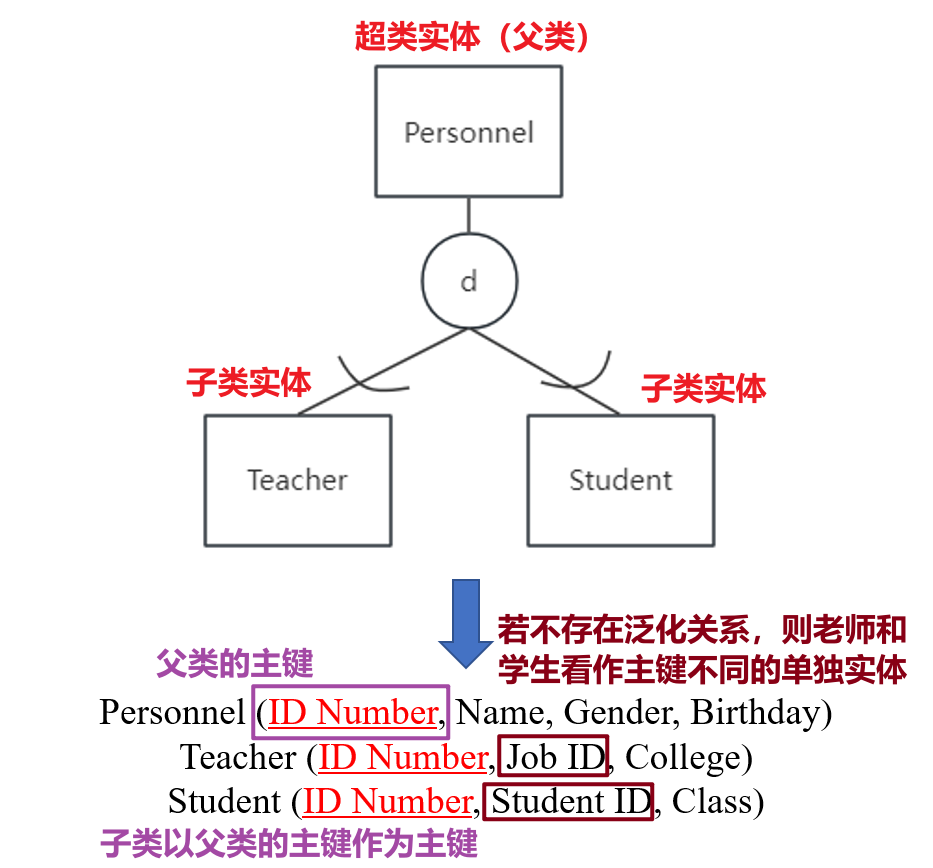
3.6 关于泛化关系

  • 泛化关系（Generalization Relationship）
    • 超类与子类
      • 抽取多个实体的共同属性组成的超类实体（Superclass Entity）
      • 子类实体是泛化层次关系中的低层次实体，对超类实体中的属性进行继承与添加
    • 重叠性约束（Disjointness Relationship）
      • 表示各个子类实体型之间是否是排他的
      • 若为排他的则用字母d标识，否则用o标识（表示Overlap）
    • 完备性约束（Completeness Relationship）
      • 表示所有子类实体型在当前系统中是否能完全覆盖超类实体型
      • 若能完全覆盖则在超类实体型与圆圈之间用双线标识
  • 如下图所示，Personnel和Person是超类实体
    • Personnel无法被子类完全覆盖，其两个子类相互独立
    • Person能被子类完全覆盖，其两个子类存在重叠

泛化属性.png

四、关系模型

关系模型（Relational Model）是一种逻辑数据模型

4.1 关系的定义

  • 给定一组域$D1​,D_2​,…,D_n$​，笛卡尔积$D_1\times D_2\times …\times D_n$的子集称为域$D1​,D_2​,…,D_n$​上的关系（Relation），表示为$R(D1,D2,…,Dn)$，其中$R$为关系名，$n$为关系的度
    • $n=1$时，称为一元关系（Unary Relation）
    • $n=2$时，称为二元关系（Binary Relation）
  • 二维表是关系模型的数据结构
    • 每行称为一个元组（Tuple）
    • 每列称为一个属性（Attribute）
    • 元组中的一个属性值称为一个分量（Component）

4.2 关系的键

  • 超键（Super Key）
    • 关系中某个属性或属性组的值能唯一标识一个元组，则该属性或属性组称为超键
  • 候选键（Candidate Key）
    • 候选键是更严格的超键，若关系中某个超键在去掉任一属性后不再成为超键，则其称为候选键
      • 单属性键（Single Attribute Key）：只包含一个属性的候选键
      • 多属性键（Multi Attribute Key）：由多个属性组成的候选键
      • 全键（All Key/Full Key）：关系中唯一的候选键且包含关系的所有属性
    • 关系的属性可按照是否存在于候选键中而分类
      • 主属性（Prime Attribute）：候选键中的属性
      • 非键属性（Non-key Attribute）：不包含在任何候选键中的属性
  • 主键（Primary Key）
    • 若关系有多个候选键，选择其中一个作为主键，可见主键是更严格的候选键
  • 外键（Foreign Key）
    • 若关系$R$中的属性或属性组$A$不是$R$的候选键，而是另一个关系$S$的候选键
      • 则$A$称为$R$的外键
      • $R$称为引用关系（Referencing Relation）
      • $S$称为被引用关系（Referenced Relation）
    • 例如下例中，选修课（R）的属性StudentID不是选修课的候选键，而是学生（S）的候选键
1
2

选修课(CourseName, CourseID, StudentID)
学生(StudentName, StudentID)

4.3 关系的特性

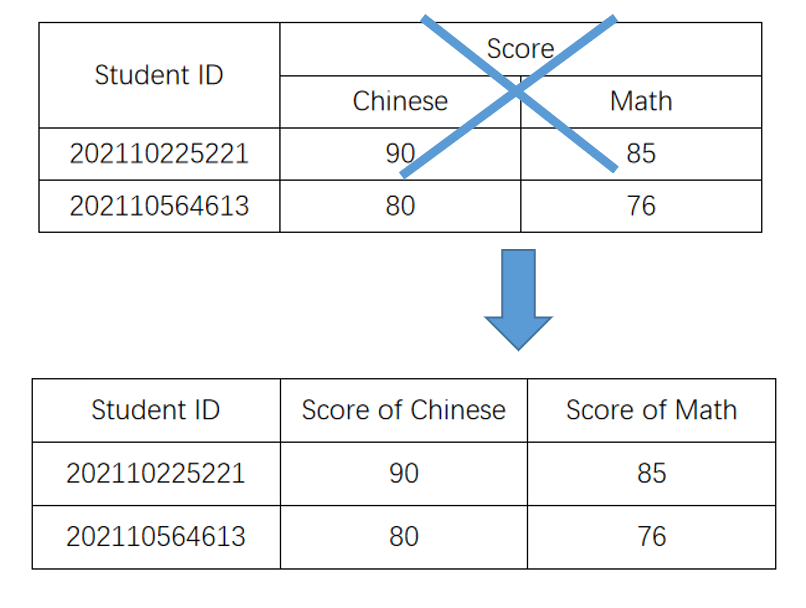
4.3.1 分量原子性

  • 关系中元组（关系是一组元组的集合，即一组数据项的集合）的每个分量必须是不可分的数据项，即具有分量原子性（Component Atomicity）

关系的组件原子性.png

4.3.2 关系是集合

  • 既然关系是数据项元组的集合，那么关系中的元组满足集合的三大性质
    • 元组有限性（Tuple Finiteness）
      • 关系中元组的数量是有限的，因为计算机无法处理无限数据
    • 元组唯一性（Tuple Uniqueness）
      • 关系中的每个元组都是唯一的，因为现实不存在完全相同的实体
    • 元组无序性（Tuple Order Arbitrariness）
      • 关系中元组的顺序可任意交换，但实际常会排序以提高效率

4.3.3 属性的特性

  • 关系规定了每个数据项的属性，即每个元组的分量
    • 属性同质性（Attribute Homogeneity）
      • 关系中同一列的数据必须具有相同数据类型且来自相同域
    • 属性名唯一性（Attribute Name Uniqueness）
      • 关系中不能有两个相同名称的属性（即使来自相同域也必须用不同名称区分）
    • 属性无序性（Attribute Order Arbitrariness）
      • 属性的顺序不影响关系模式的实际含义（但定义后属性值的顺序不能随意交换）

4.4 关系完整性约束

  • 关系完整性（Relational Integrity）约束规则目的是保证关系的正确性、有效性、兼容性
    • 实体完整性（Entity Integrity）用来保证实体是可识别的，即主键属性不能为空
      • 例如学生关系中的[学号]主键不能为空，选课关系中的[学号,课程号]组合主键中的两者都不能为空
    • 参照完整性（Referential Integrity）用来保证数据间的关联正确，即外键要么为空，要么等于被引用关系中某个主键值
      • 例如选课关系中的[课程号]是其外键，必须等于课程关系中某个主键值
    • 用户定义完整性（User Defined Integrity）用来保证数据取值合理，体现为用户针对具体应用定义的约束条件
      • 例如学生关系中性别只能是男或女、课程关系中课时和学分不能小于$0$、选课关系中成绩应在$[0,100]$区间内等约束

4.5 E-R模型转关系模型

4.5.1 转换方法

  • 为了将E-R图转换为关系模型
    • 实体型与实体属性
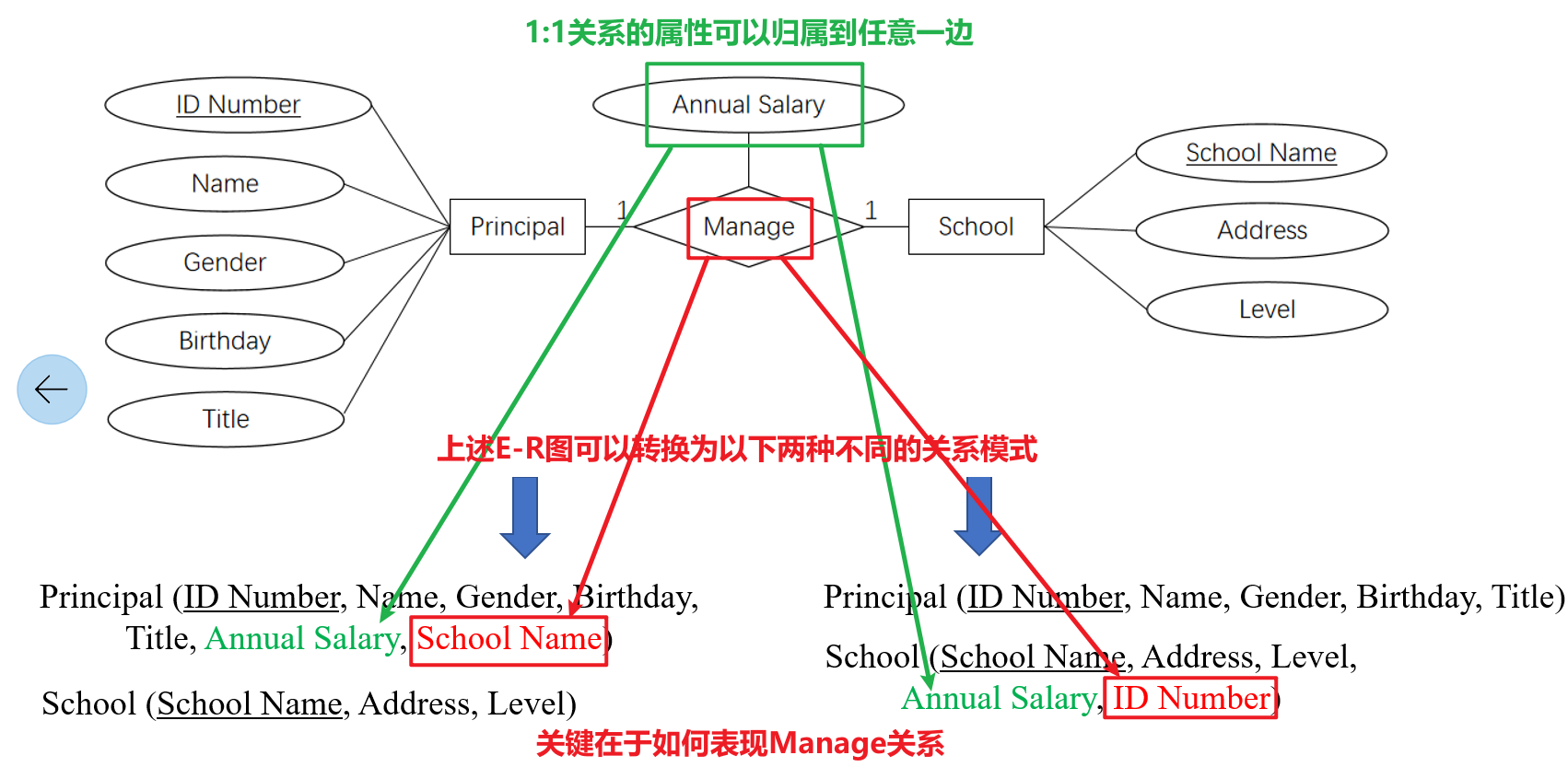
      • 将E-R图中的每个实体型转换为一个关系模式，如下图的校长与学校
      • 关系模式中需要至少包含E-R图中对应实体型的所有属性
      • 取用E-R图中对应实体型的唯一标识符作为关系模式的主键
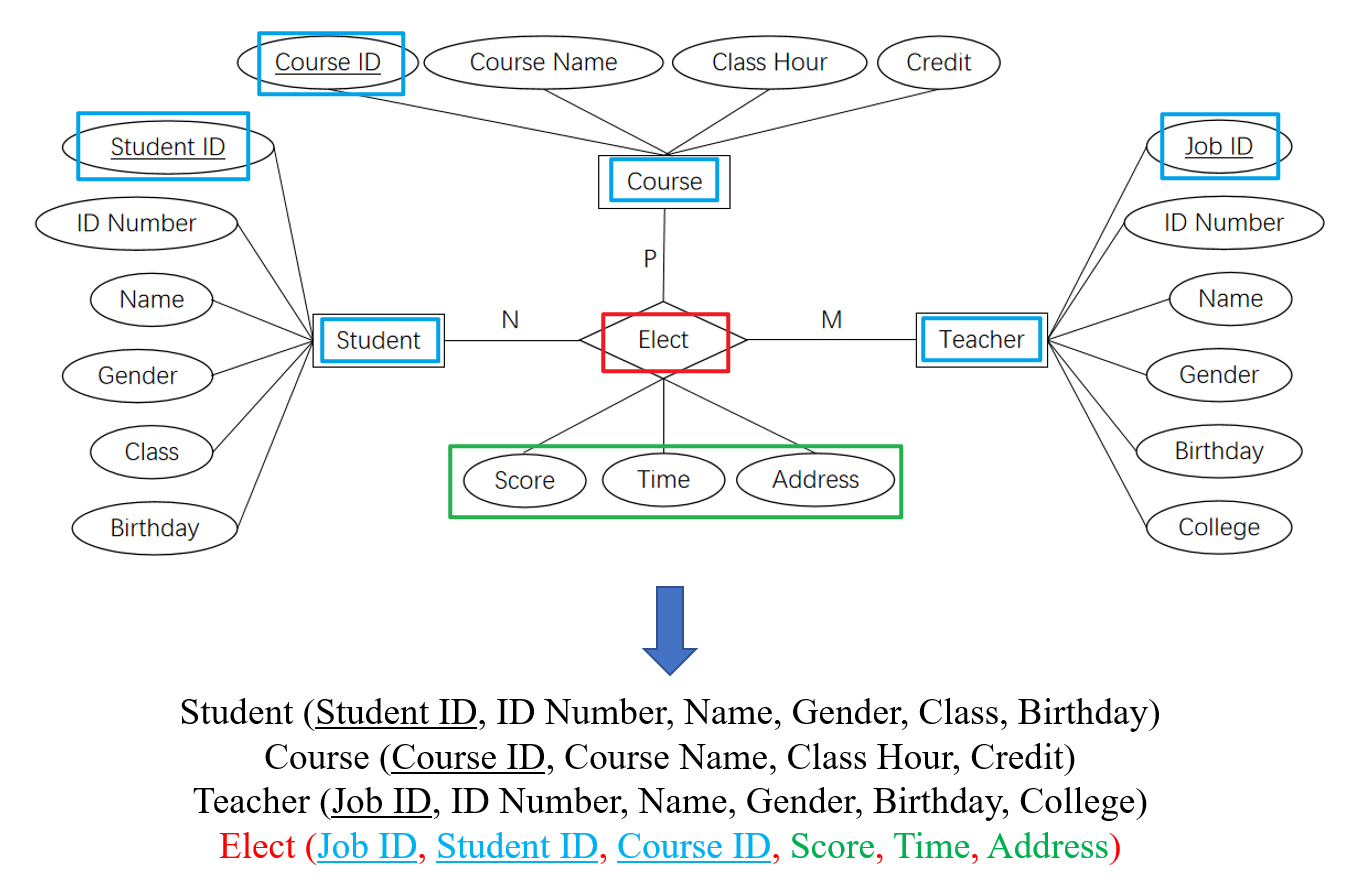
    • 关系型与关系属性
      • E-R图中的不同二元关系类型（1:1、1:N、M:N）需具体处理

4.5.2 一对一

  • 以下是不同实体型间的1:1关系转换的示例

一对一多实体型E-R图转换为关系模式.png

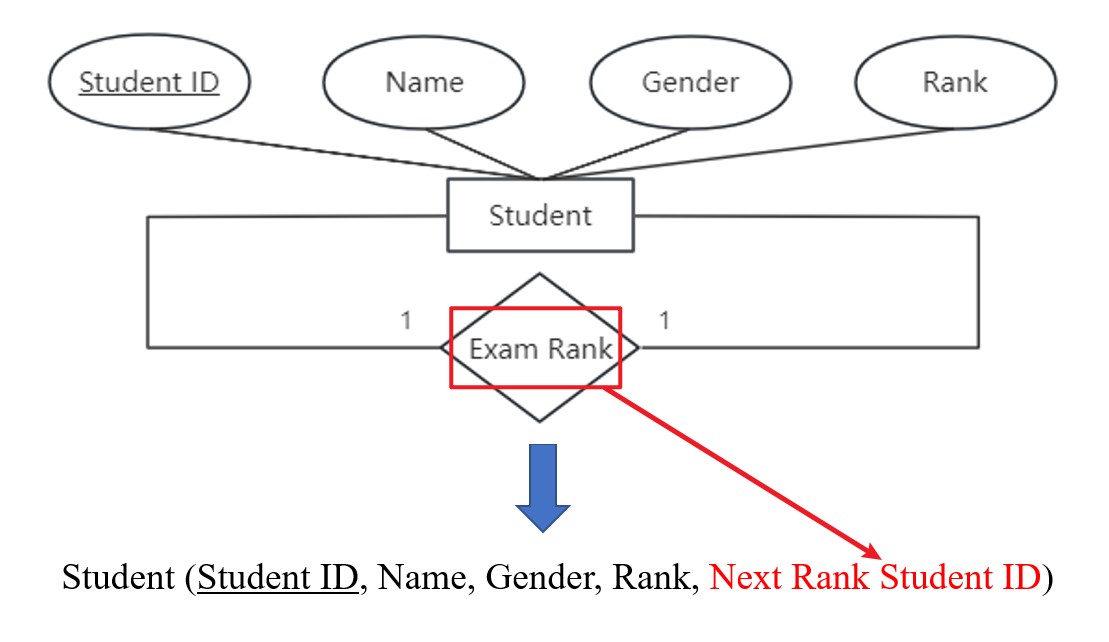
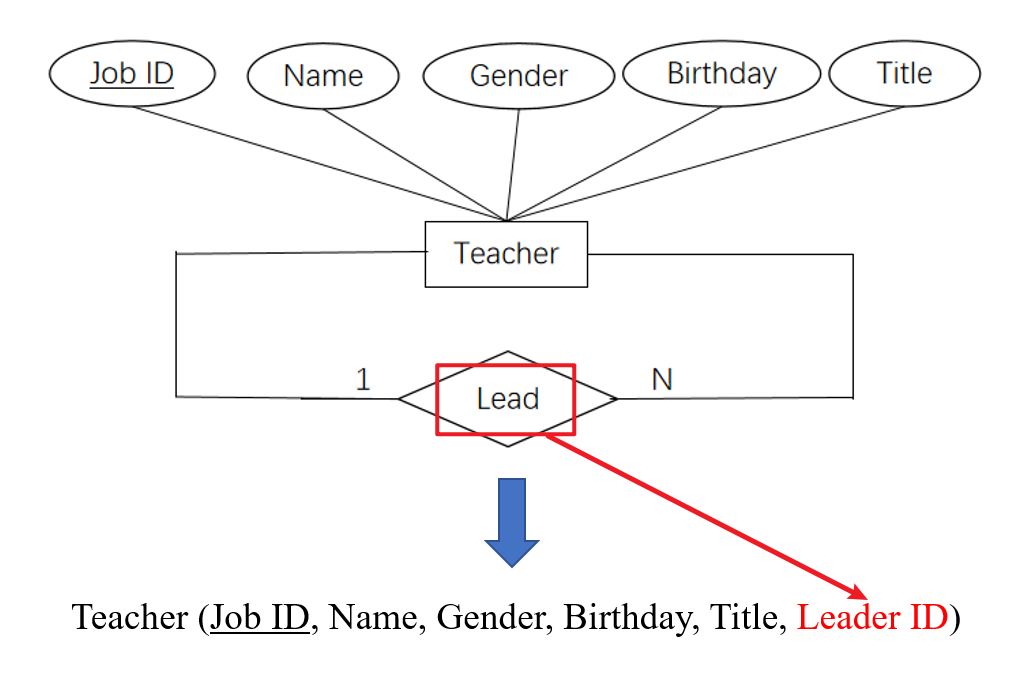
  • 以下是单个实体型间1:1关系转换的示例

一对一单实体型E-R图转换为关系模式.png

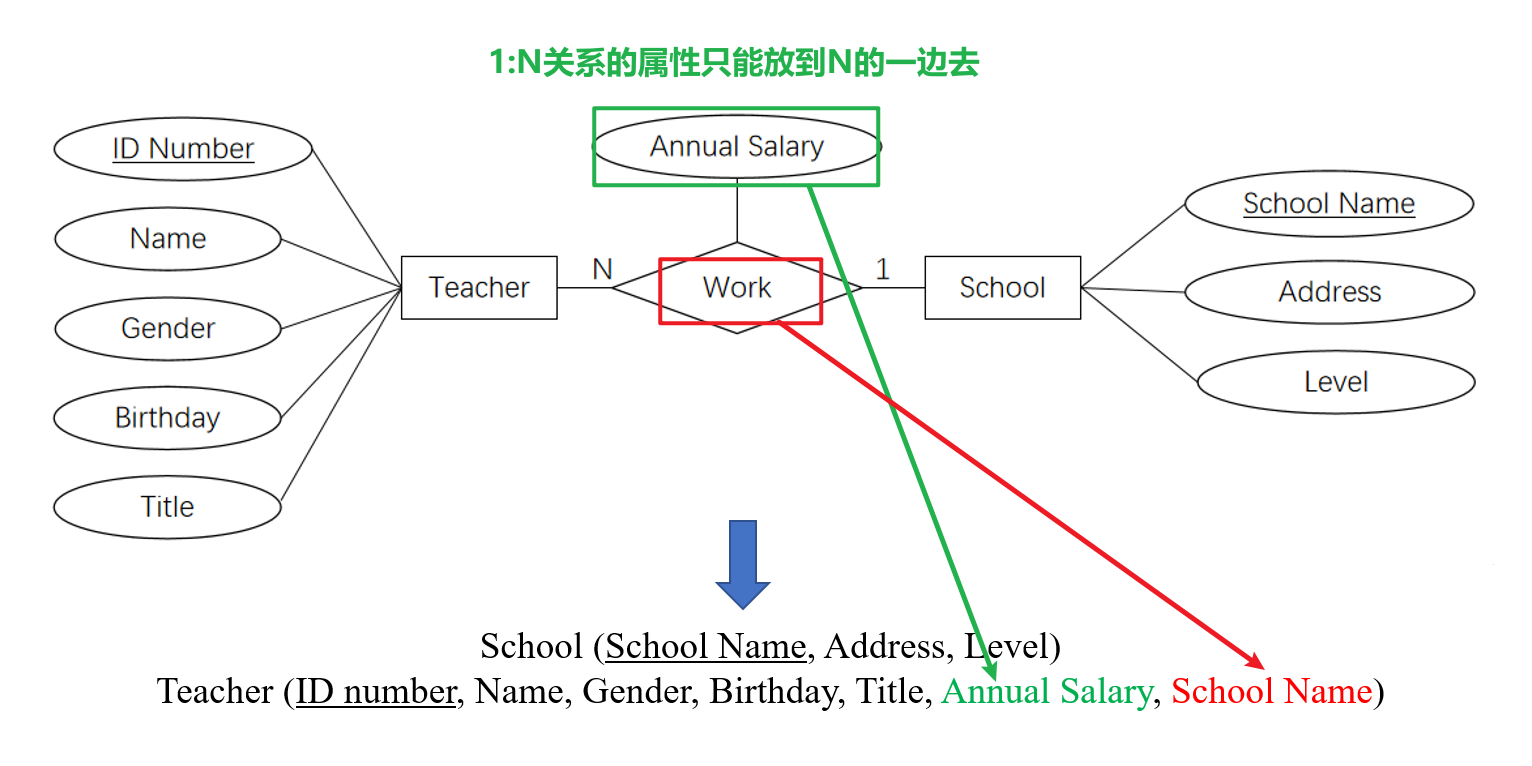
4.5.3 一对多

  • 以下是不同实体型间的1:N关系转换的示例

一对多多实体型E-R图转换为关系模式.png

  • 以下是单个实体型间1:N关系转换的示例

一对多单实体型E-R图转换为关系模式.png

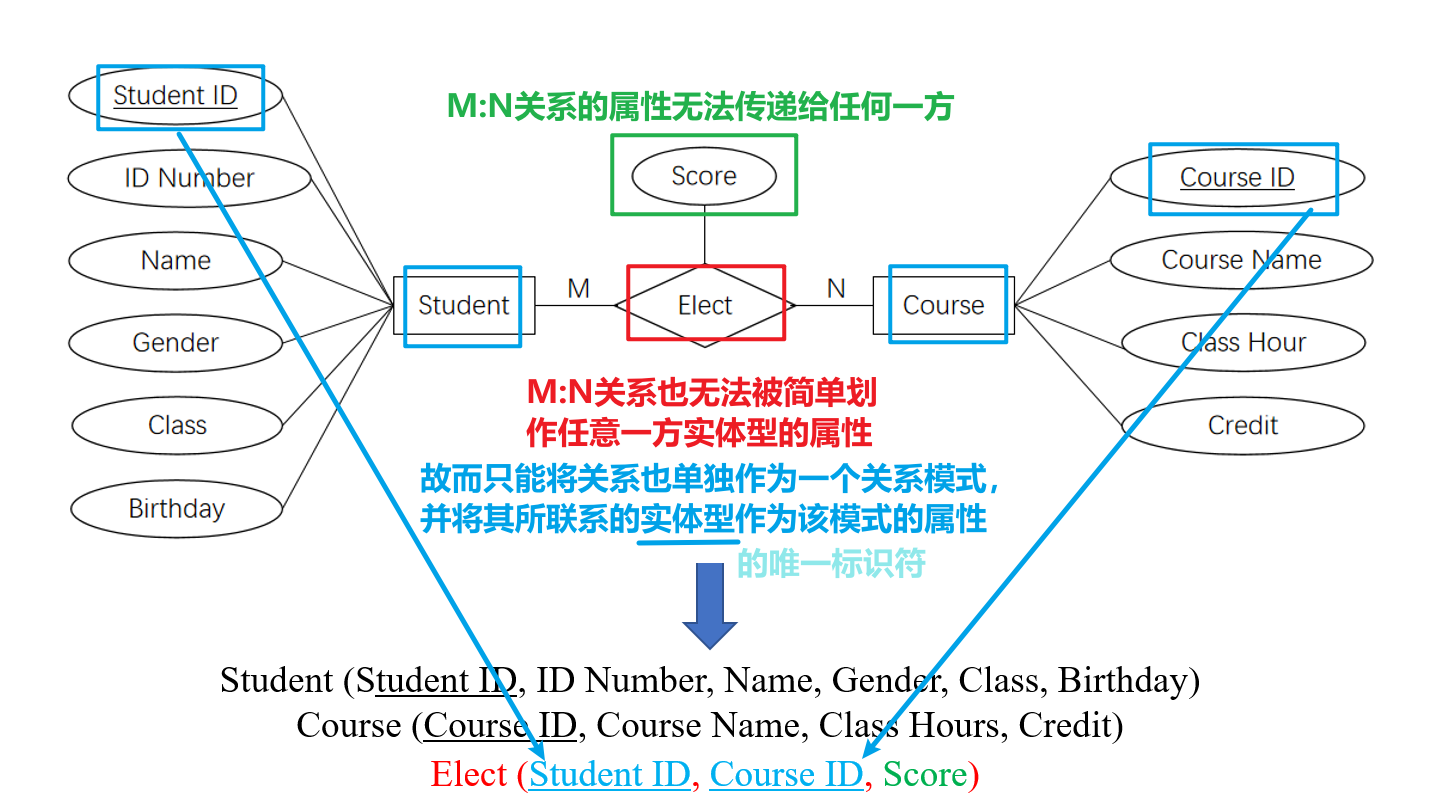
4.5.4 多对多

  • 以下是不同实体型间的M:N关系转换的示例

多对多多实体型E-R图转换为关系模式.png

更复杂多对多多实体型E-R图转换为关系模式.png

4.5.5 泛化关系

  • 以下是泛化关系E-R图转化为关系模型的示例

泛化关系E-R图转化为关系模式.png

五、关系代数

关系代数（Relational Algebra）是一组针对关系模型的操作

5.1 集合操作

5.1.1 并集

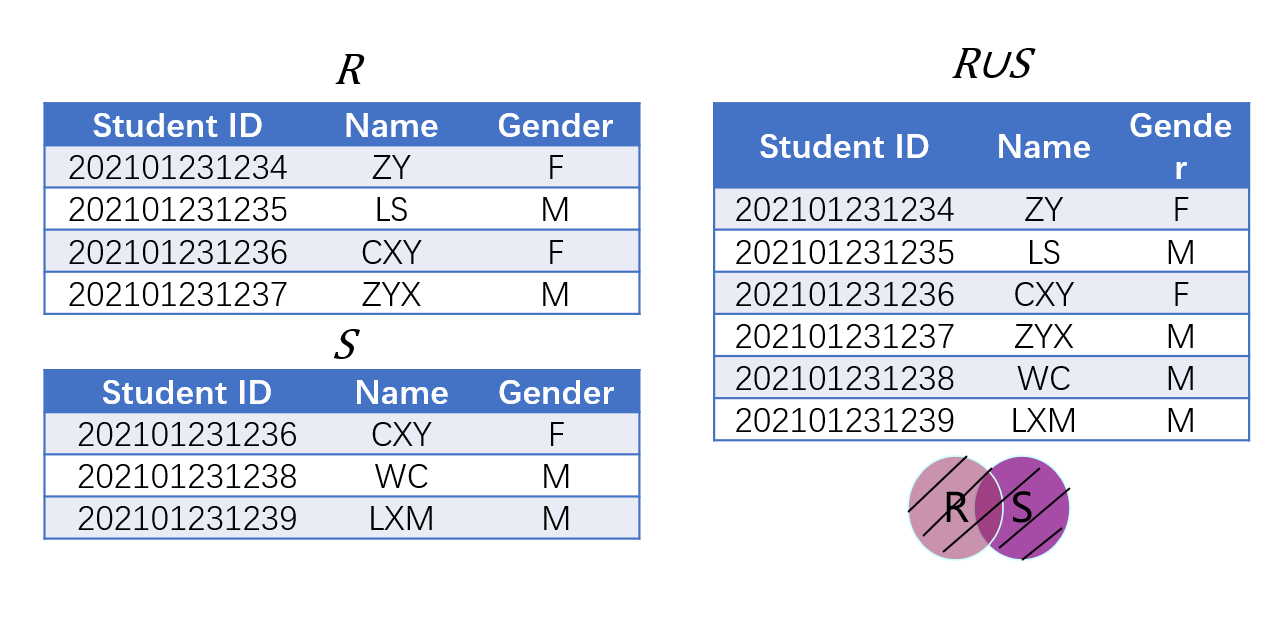
  • 并集（Union）取两集合（元素必须具有同一关系模式）所覆盖的所有不重复数据，记作$R\cup S$

并集操作.png

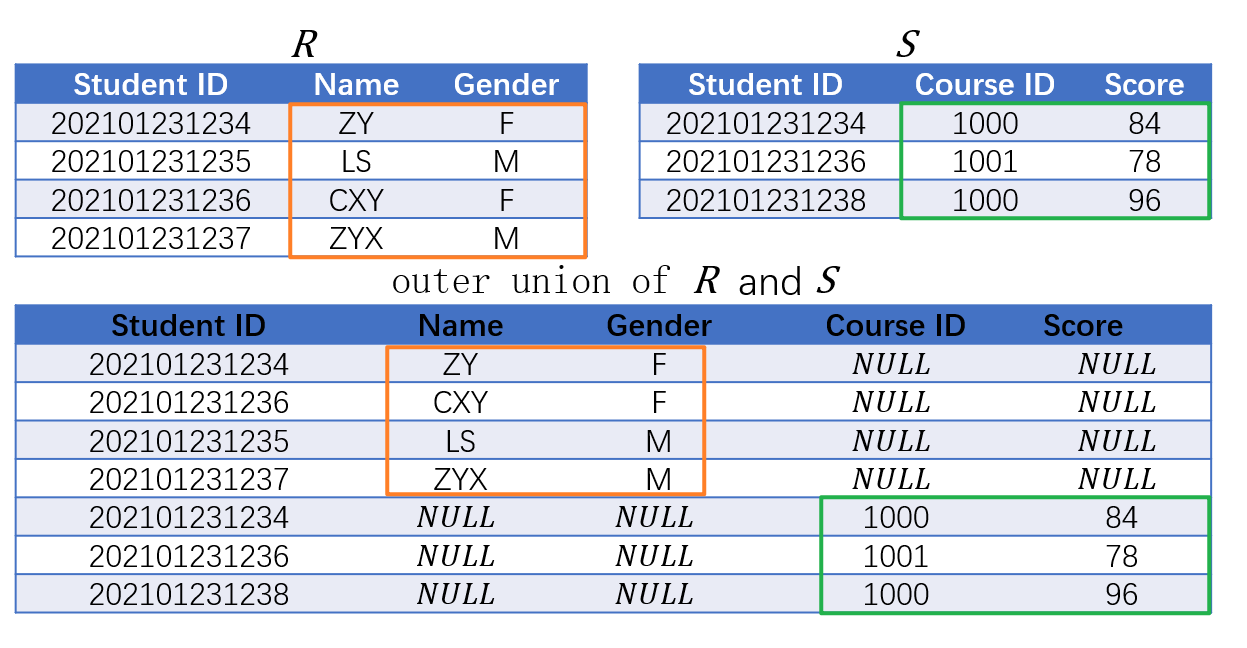
  • 外并集（Outer Union）则无需元素具有同一关系模式，直接合并即可，不用有的属性则置空

外并集.png

5.1.2 交集

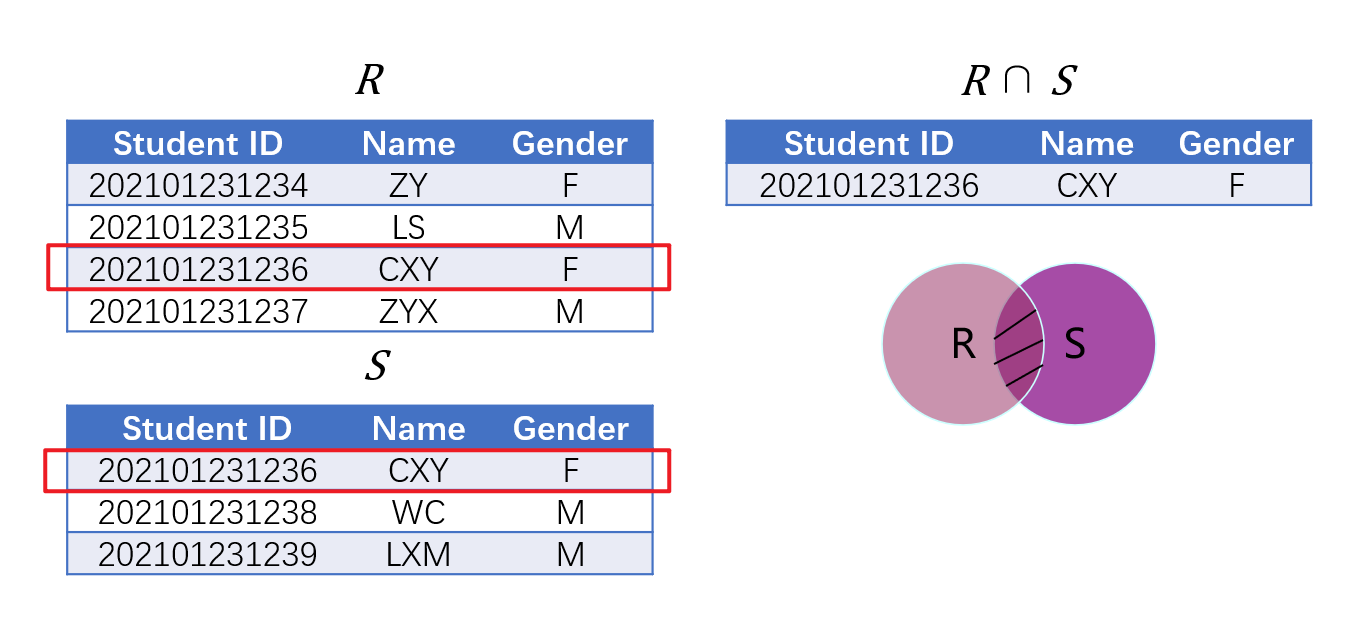
  • 交集（Intersection）取两集合（元素必须具有同一关系模式）中共同拥有的数据，记作$R\cap S$

交集操作.png

5.1.3 差集

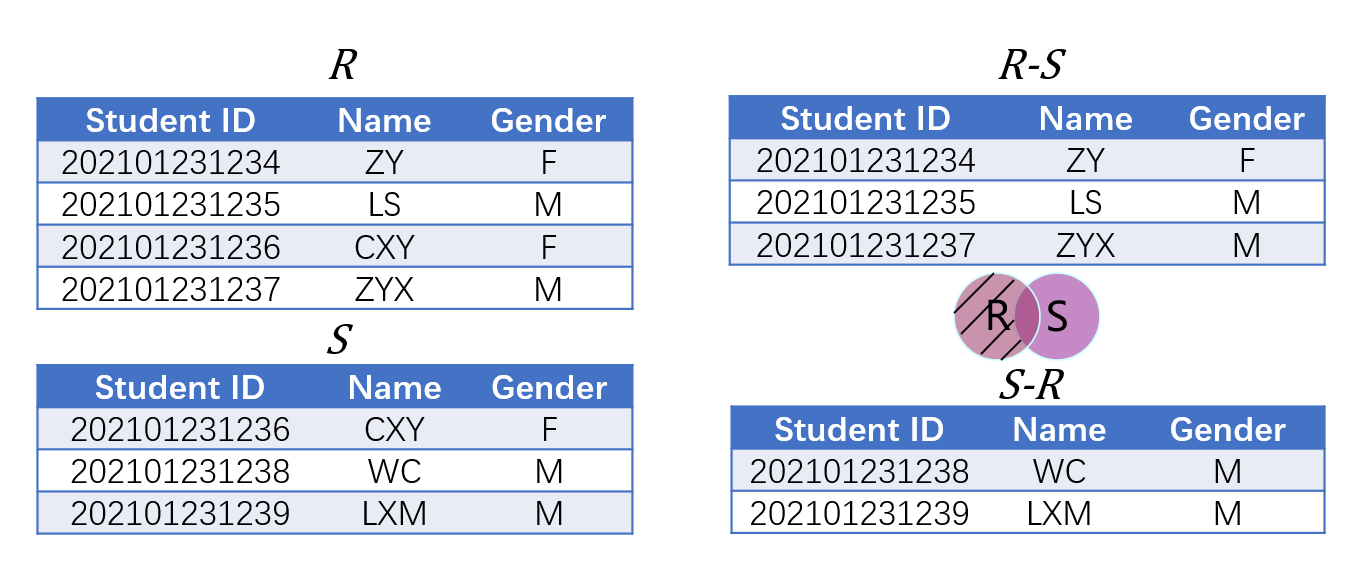
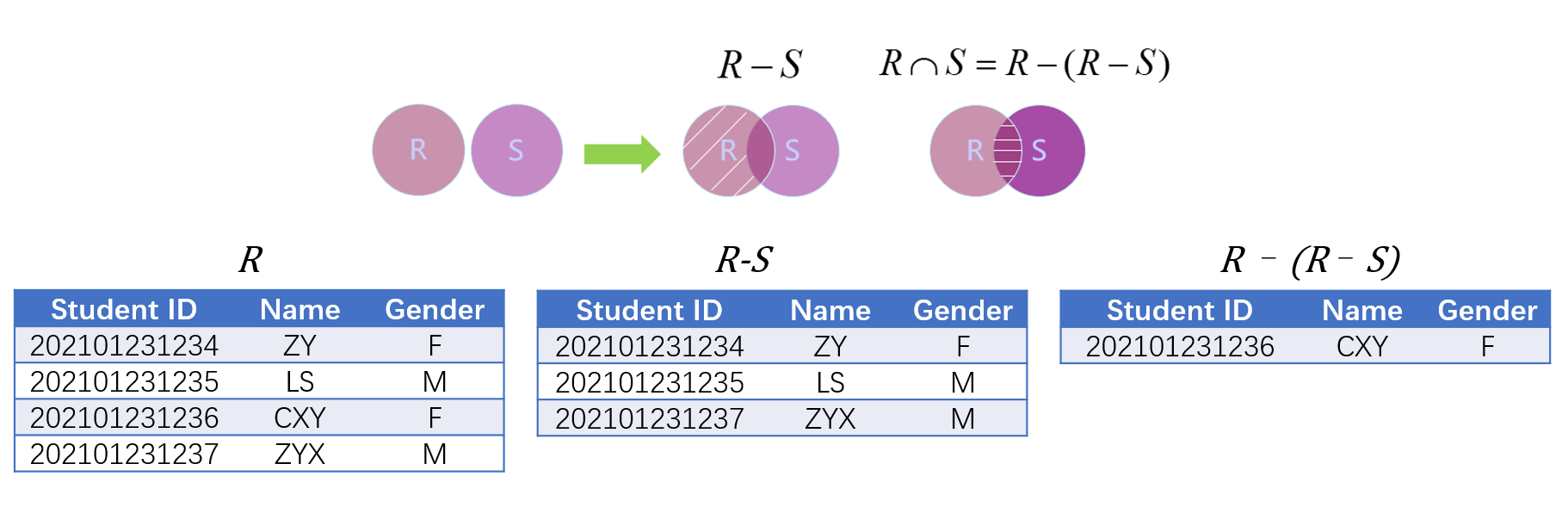
  • 差集（Difference）选取两集合（元素必须具有同一关系模式）中独属于其中某一个集合的数据，记作$R-S$

差集操作.png

  • 交集可以通过差集实现，即$R\cap S = R-(R-S)$

用差集操作表示交集.png

5.2 筛选裁切

5.2.1 选择

  • 选择（Selection）操作从关系$R$（数据表）中筛选满足特定条件$F$的元组（数据项），记作$\sigma_F(R)$

选择操作.png

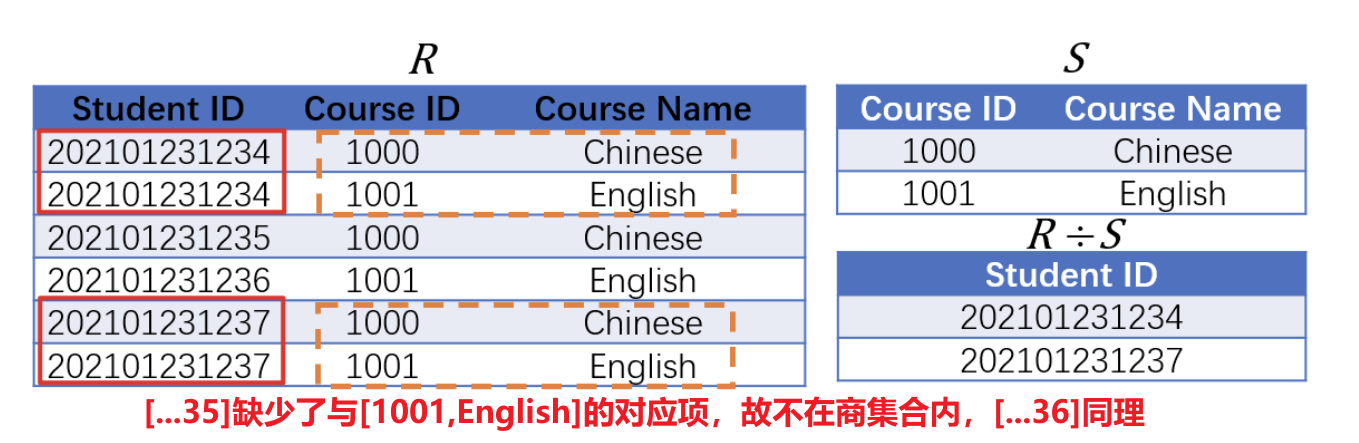
5.2.2 除法

  • 两组关系（数据集合）间的除法（Division）记作$R\div S$，用于查询满足特定条件的所有元组
    • 选择运算
      • 只对一个关系操作，根据指定条件从关系中选取满足条件的元组
      • 不改变关系的属性结构，只是过滤元组
    • 除法运算
      • 对两个关系操作，找出一个关系中与另一个关系所有元组都关联的元组
      • 会改变关系的属性结构（新表元素的关系模式不同），结果只包含$R$中不属于$S$的属性

除法操作.png

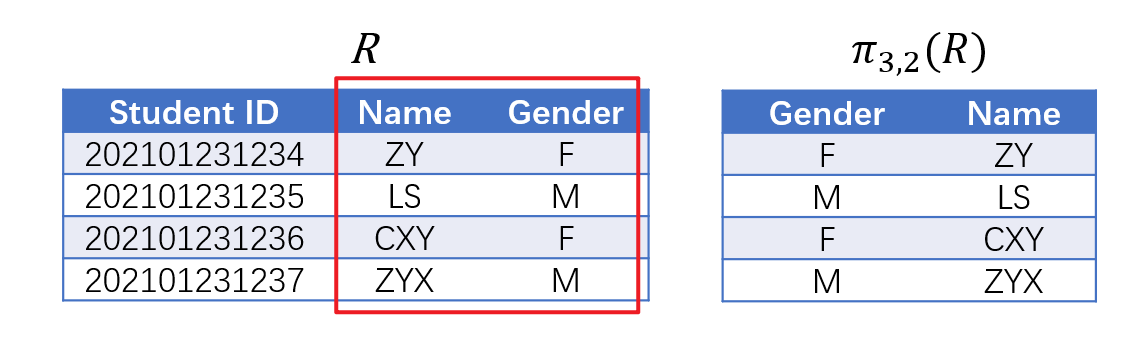
5.2.3 投影

  • 投影（Projection）操作从关系$R$（数据表）中仅选取特定属性列（保留所有数据项），记作$\pi_A(R)$

投影操作.png

5.3 笛卡尔积

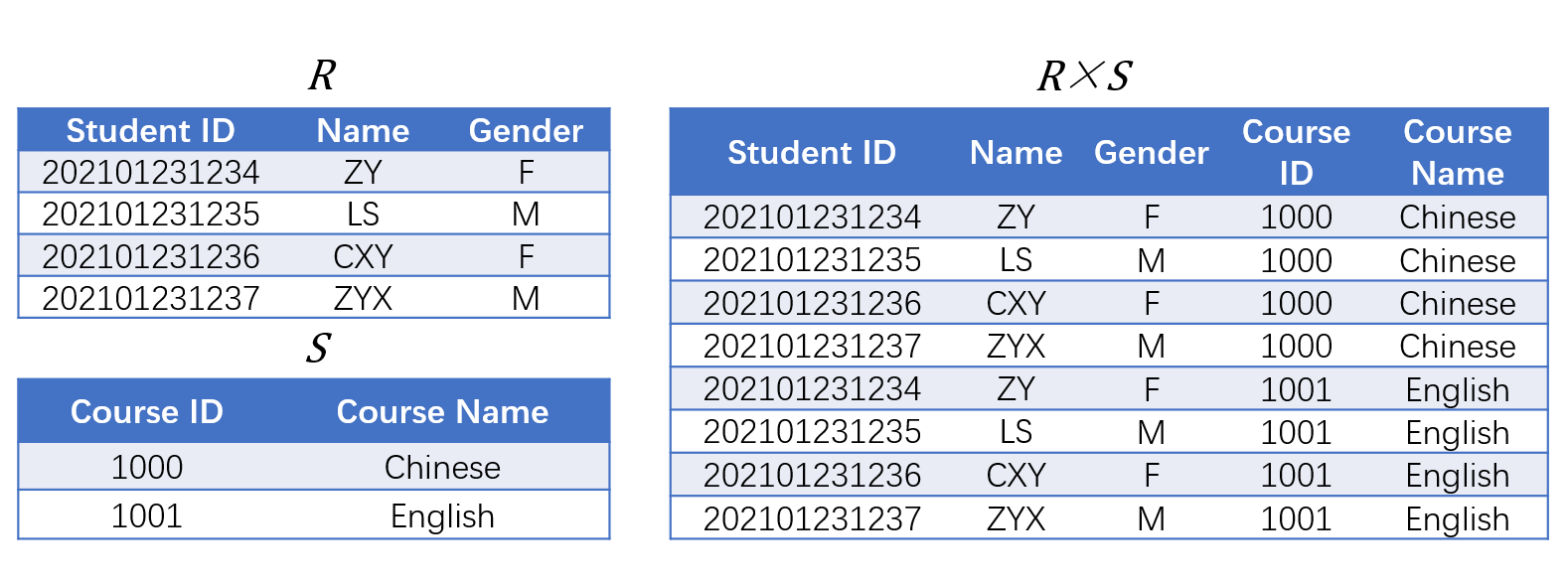
  • 笛卡尔积（Cartesian Product）将两集合（元素无需一定属于同一关系模式）中的元素数据逐一配对成新元素（积集合元素数等于原集合元素数之积），记作$R\times S$

笛卡儿积.png

5.4 连接操作

5.8.1 等值连接

  • 连接（Join）操作通过限制表与表之间的属性间的关系，从表之间的笛卡尔积集合中选取部分数据项，形成一张新的表，例如表$R$和$S$通过条件$i\theta j$限制，记作$R\Join_{i=j}S$，注意是\Join
    • $i$表示$R$的第$i$列属性
    • $j$表示$S$的第$j$列属性
    • $\theta$是比较运算符（如$=$、$<$、$\geq$等）
  • 等值连接（Equivalent Join）指的是$\theta$为$=$的连接操作，即期望在笛卡尔积$R\times S$中，找到表$R$的第$i$列属性值与表$S$的第$j$列属性值相等的数据项

等值连接操作.png

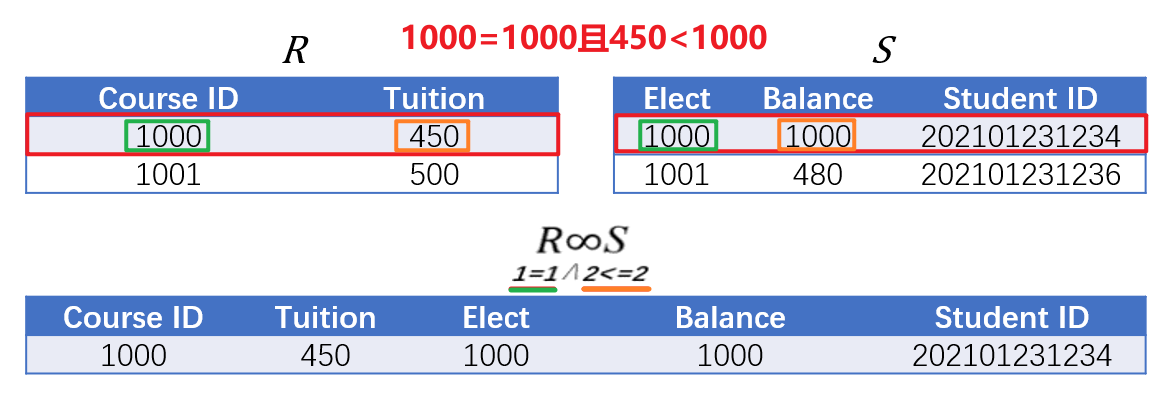
5.8.2 $F$连接

  • $F$连接（F Join）指的是表$R$和$S$通过条件$F$关联，$F$是通过逻辑与运算$\wedge$复合$i\theta j$的逻辑表达式
\[F=F_1\wedge F_2\wedge...\wedge F_n\]

F连接操作.png

5.8.3 自然连接

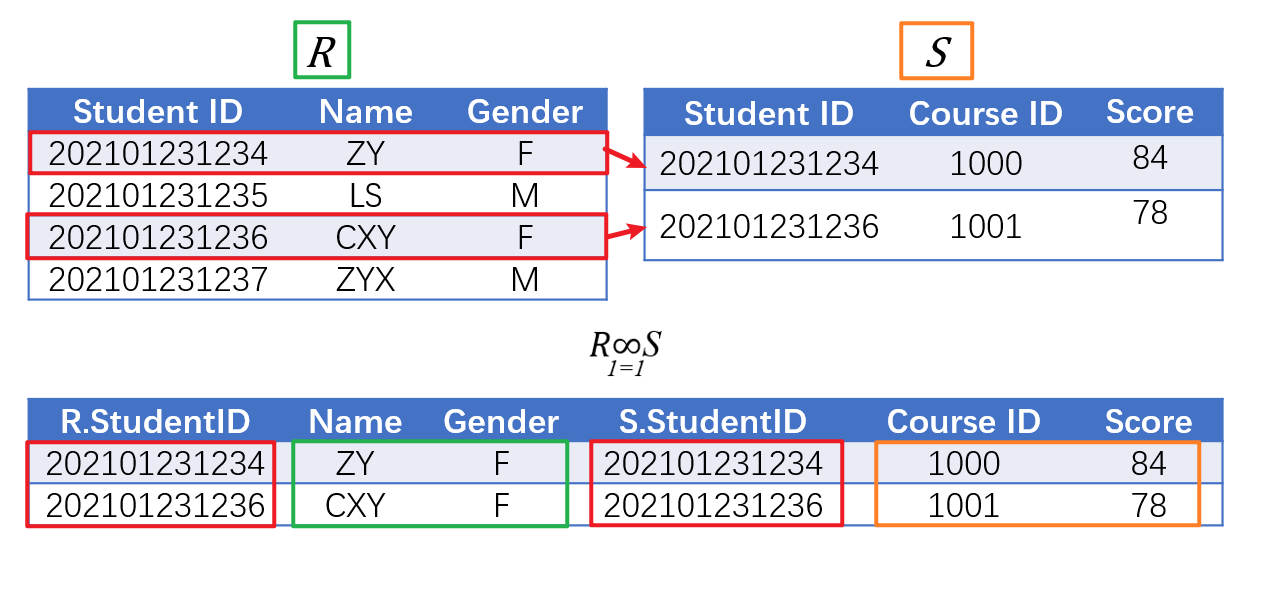
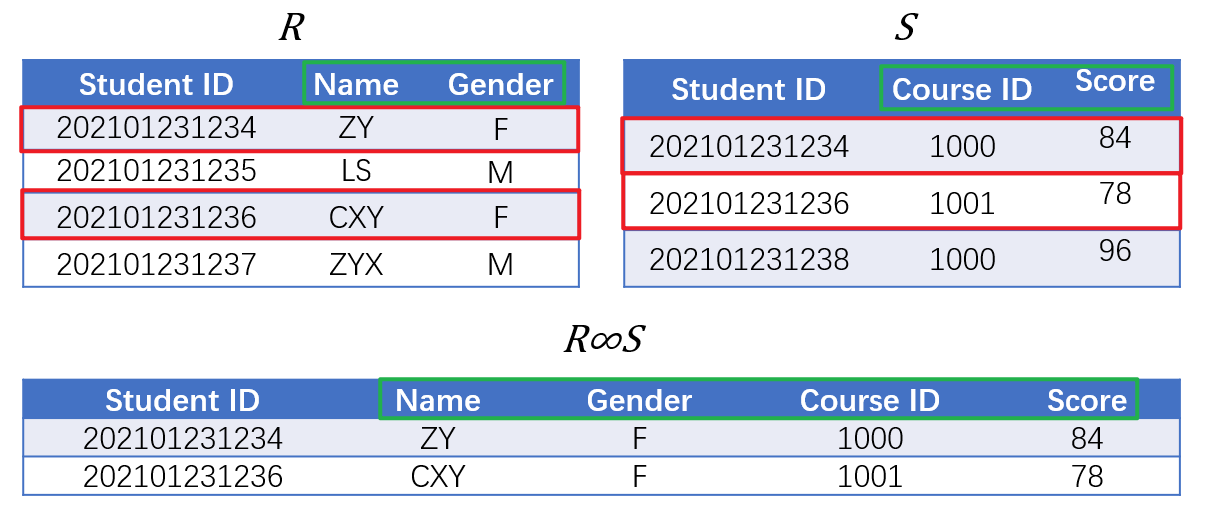
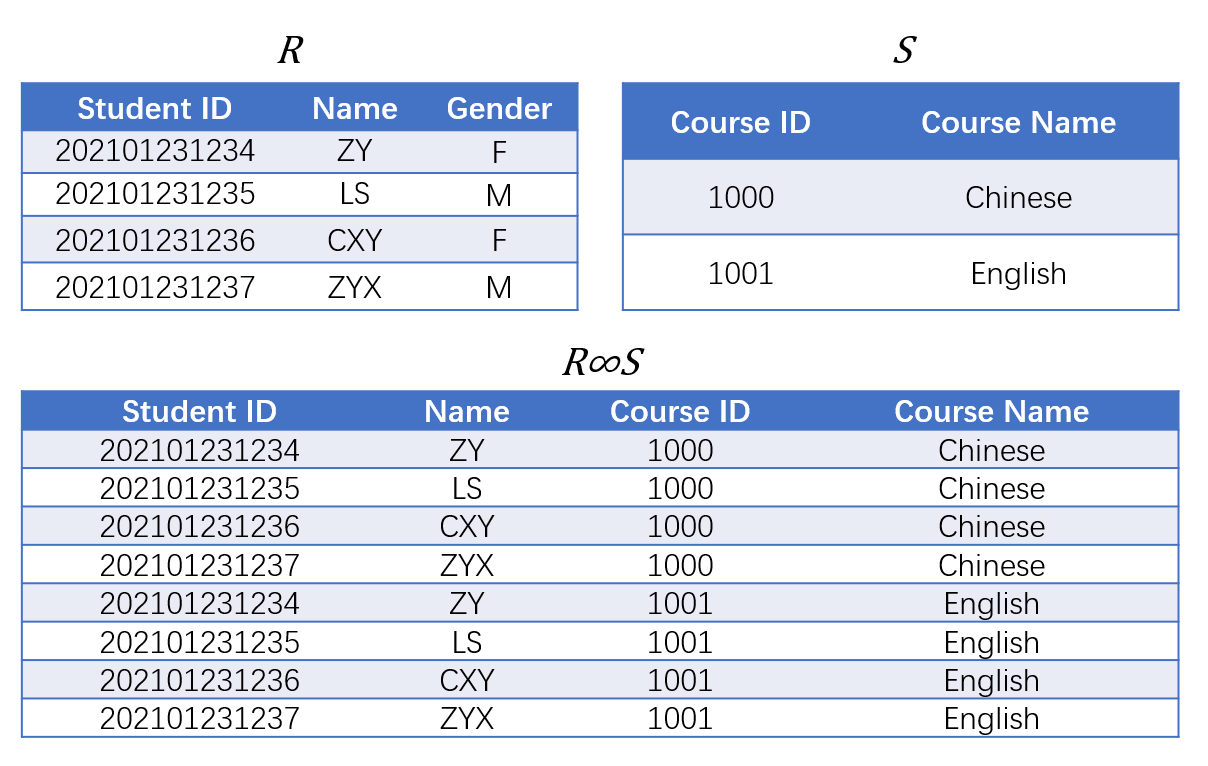
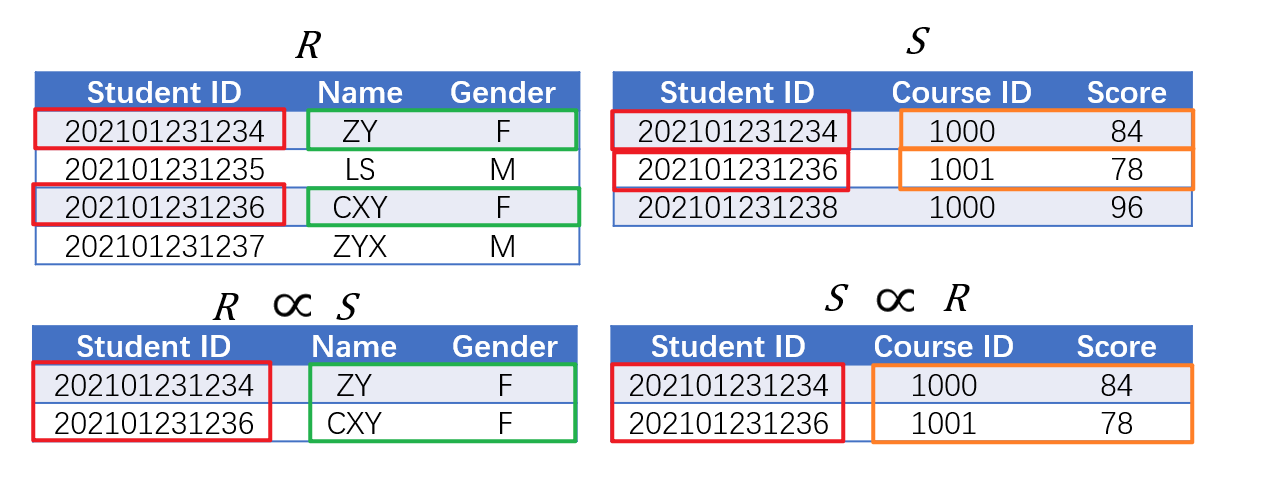
  • 若两表中存在相同属性，则其自然连接（Natural Join）指的是
    • 从二者笛卡尔积中选取满足全部（如果存在多个共有属性则需全部相等）共有属性（例如下图的共有属性是Student ID）的值均相等的所有数据项
    • 且每个共有属性均只保留一份，形成新的表，也就是说自然连接所得集合中的元素与笛卡尔积中的元素在关系模式上并不一致
  • 自然连接记作$R\bowtie S$，注意是\bowtie，与一般连接\Join存在差异

自然连接操作.png

  • 若两表中不存在共同的属性，则自然连接退化为笛卡尔积$R\times S$

自然连接操作退化为笛卡尔积.png

5.8.4 外连接

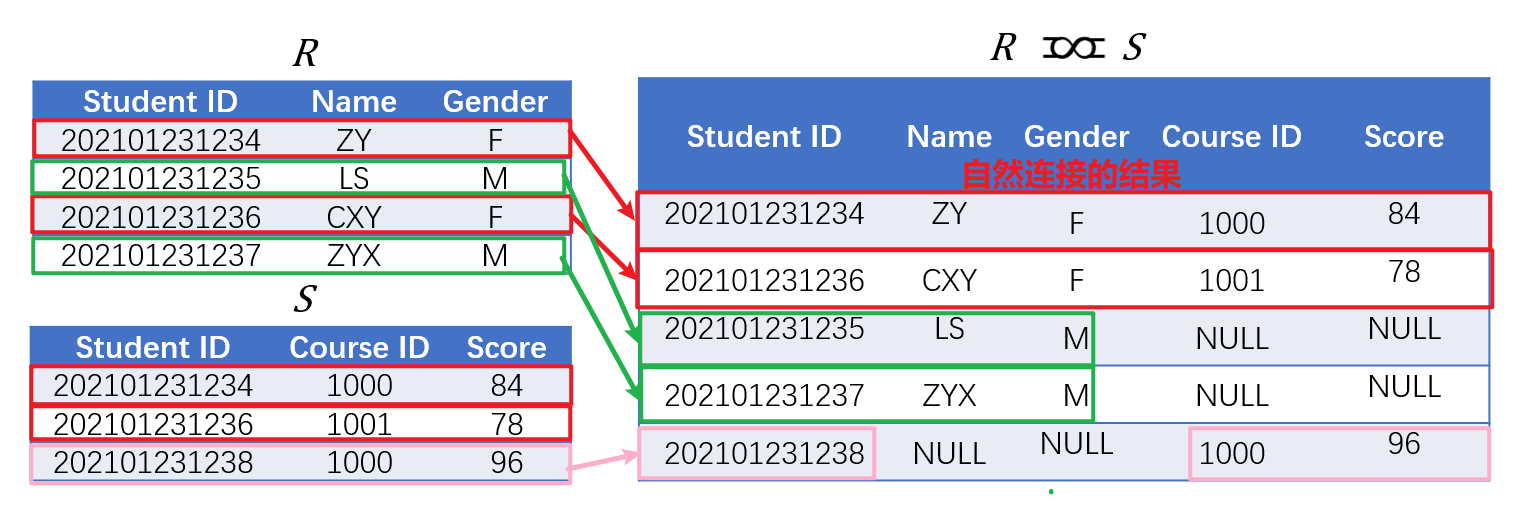
  • 全外连接（Outer Join）记作\mathrel{\fullouterjoin}，其在自然连接\bowtie基础上，保留$R$和$S$中原本要舍弃的元组（不是笛卡尔积）全部放到结果集合中，$R$中不包含的$S$的属性或$S$中不包含的$R$的属性的值均用空值NULL填充

外连接操作.png

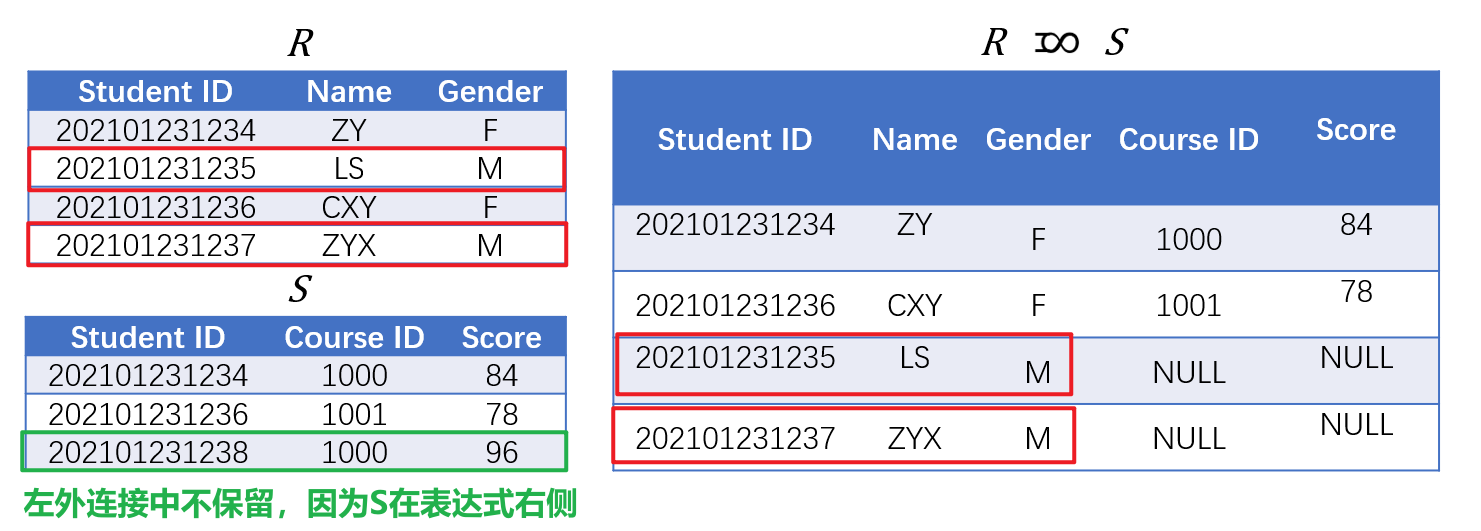
  • 左外连接（Left Outer Join）记作$R\mathrel{\ltimes}S$，弱于外连接，仅保留$R\mathrel{\ltimes}S$中左侧$R$原本要舍弃的元组

左外连接操作.png

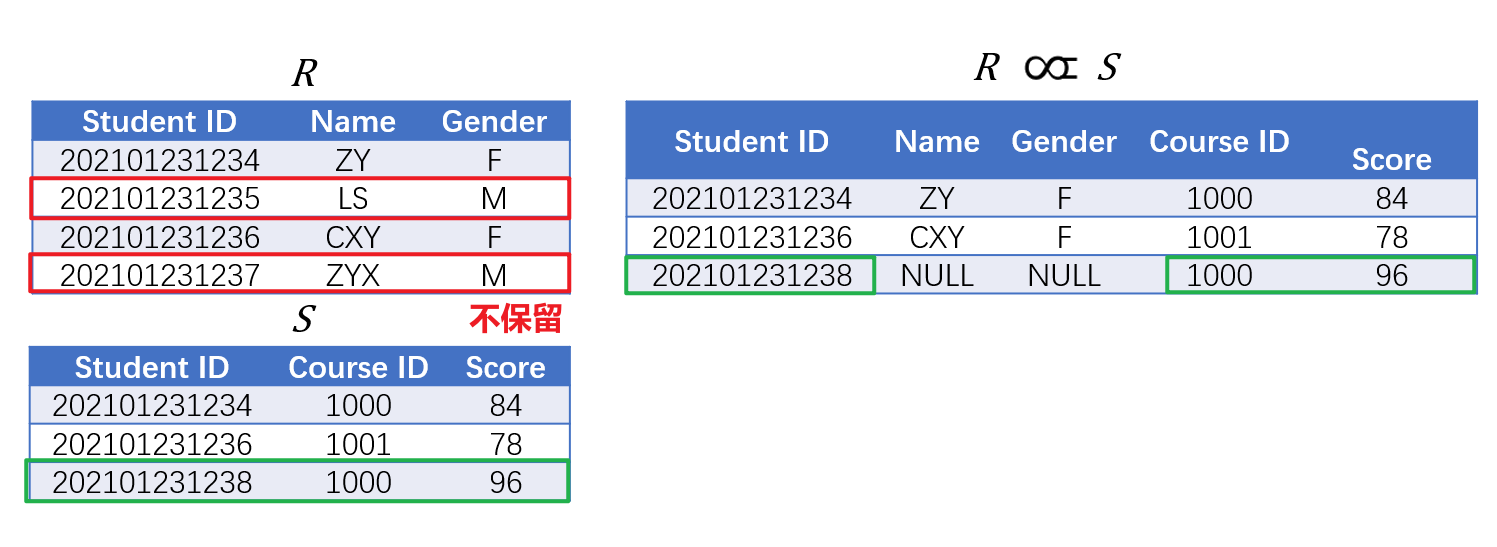
  • 右外连接（Right Outer Join）记作$R\mathrel{\rtimes}S$，弱于外连接，仅保留$R\mathrel{\rtimes}S$右侧$S$原本要舍弃的元组

右外连接操作.png

5.8.5 半连接

  • 左半连接（Left Semi Join）记作$\ltimes$，基于$R$和$S$的自然连接，但是只保留左侧$R$中符合的元组，且不包含右侧$S$中的属性，右半连接同理类推

半连接操作.png

5.5 示例与优化

5.5.1 应用案例

  • 对于以下关系模式

应用案例P1.png

  • 有以下若干操作示例

应用案例P2.png

应用案例P3.png

5.5.2 访问优化

  • 对于多个等效的复合访问操作语句，我们应当选取运行效率更优的语句使用
    • 应当尽早执行Selection和Projection操作，且尽可能同时执行二者
    • 在执行连接前，对表进行预处理，例如进行排序

访问操作优化例子.png

学科笔记, 数据库系统
数据库系统
本文由作者按照 CC BY-NC-SA 4.0 进行授权